FastMNMF及改进

FastMNMF

FastMNMF是一种基于矩阵联合对角化的MNMF的加速算法；后者在前一篇笔记中已经简略描述，是一种对NMF在音频应用上的多通道扩展。

MNMF

回顾MNMF的音频建模，MNMF认为一个音源\(s_{jfn}\)由多个表现为复高斯分布的成分\(c_{kfn}\)组成。

\[ s_{j f n}=\sum_{k \in \mathcal{K}_j} c_{k f n} \quad \text { avec } c_{k f n} \sim \mathcal{N}_{\mathbb{C}}\left(0, w_{f k} h_{k n}\right) \]

这些成分相互独立，因此源被定义为：

\[ s_{j f n} \sim \mathcal{N}_{\mathbb{C}}\left(0, \sum_{k \in \mathcal{K}_j} w_{f k} h_{k n}\right) \]

被观测信号被定义为源的线性组合：

\[ x_{ifn}=\mathcal{N}_{\mathbb{C}}\left(0,\sum_j q_{i j, f} \sum_{k \in \mathcal{K}_j} w_{f k} h_{k n}\right) \]

直接考虑\(K\)个基分量（成分），又可以将被观测信号的协方差矩阵写作：

\[ \tilde{X}_{f n}=\sum_{k=1}^K w_{f k} h_{k n} Q_{f k} \]

\(Q\)在这里表示第\(k\)个成分的空间特性矩阵，并且认为该空间特性是时不变的。需要求解的参数为\(w_{fk},h_{kn}\)和\(Q_{fk}\)，在实践中使用乘法规则进行迭代求解。

\[ \begin{aligned}&w_{f k} \leftarrow w_{f k} \sqrt{\frac{\sum_n h_{k n} \operatorname{tr}\left(\mathbf{X}_{f n}^{-1} \tilde{\mathbf{X}}_{f n} \mathbf{X}_{f n}^{-1} \mathbf{Q}_{f k}\right)}{\sum_n h_{k n} \operatorname{tr}\left(\tilde{\mathbf{X}}_{f n}^{-1} \mathbf{Q}_{f k}\right)}} , \\& h_{k n} \leftarrow h_{k n} \sqrt{\frac{\sum_f w_{f k} \operatorname{tr}\left(\mathbf{X}_{f n}^{-1} \tilde{\mathbf{X}}_{f n} \mathbf{X}_{f n}^{-1} \mathbf{Q}_{f k}\right)}{\sum_f w_{f k} \operatorname{tr}\left(\tilde{\mathbf{X}}_{f n}^{-1} \mathbf{Q}_{f k}\right)}} ,\\& \mathbf{A}_{f k}=\sum_n h_{k n} \tilde{\mathbf{X}}_{f n}^{-1} ,\quad \mathbf{B}_{f k}=\mathbf{Q}_{f k}\left(\sum_n h_{k n} \mathbf{X}_{f n}^{-1} \tilde{\mathbf{X}}_{f n} \mathbf{X}_{f n}^{-1}\right) \mathbf{Q}_{f k},\\&\mathbf{Q}_{f k} \leftarrow \mathbf{A}_{f k}^{-\frac{1}{2}}\left(\mathbf{A}_{f k}^{\frac{1}{2}} \mathbf{B}_{f k} \mathbf{A}_{f k}^{\frac{1}{2}}\right)^{\frac{1}{2}} \mathbf{A}_{f k}^{-\frac{1}{2}}. \end{aligned} \]

如上操作可以将被观测信号分解为基分量，但我们期望其分解为源信号。为此需要将基分量聚类到各个音源上去，这一过程被称为基础分量聚类。

考虑将第\(k\)个基分量的空间特性矩阵\(Q_{fk}\)分解为各个音源贡献之和：

\[ Q_{f k}=\sum_{r=1}^R z_{k r} G_{f r} \]

其中\(z_{kr}\)是第\(r\)个声源对基分量\(k\)的责任度，\(G_{fr}\)是第\(r\)个音源在频率为\(f\)时的空间特性矩阵。原本的被观测信号的协方差矩阵写作：

\[ \hat{X}_{f n}= \sum_{r=1}^R\left(\sum_{k=1}^K z_{k r} w_{f k} h_{k n}\right) G_{f r} \]

在\(\left\{w_{f k}, h_{k n}, z_{k r}, G_{f r}\right\}\)参数组估计完成之后，可以使用多通道Wiener滤波估计第\(r\)个音源的STFT：

\[ \hat{y}_{f n}^{(r)}=\hat{X}_{rf n}\hat{X}_{f n}^{-1} x_{f n}=\left(\sum_{k=1}^K z_{k r} w_{f k} h_{k n}\right) G_{f r} \hat{X}_{f n}^{-1} x_{f n} \]

更新方式可以参考原论文。

上述提及多次的空间特性矩阵，本质上为Spatial Covariance Matrix，SCM，也就是空间协方差矩阵，之后我们可能会混合使用这些名词。设声源\(r\)在频率\(f\)上，各个麦克风的复幅矢量（complex STFT vector ）为\(s_{f r n}=\left[s_{1 f r n}, \ldots, s_{M f r n}\right]^{\mathrm{T}}\)，则其空间特性矩阵的理想定义为：

\[ G_{f r}=\mathbb{E}\left[s_{f r n} s_{f r n}^{\mathrm{H}}\right] \]

因此，空间特性矩阵是一个\(G_{fr}\in \mathbb C^{M\times M}\)的矩阵，这里的\(M\)表示麦克风数量。其对角元给出各通道功率，非对角元给出通道间相关性。

如上述公式\(\hat{X}_{f n}= \sum_{r=1}^R\left(\sum_{k=1}^K z_{k r} w_{f k} h_{k n}\right) G_{f r}\) 中：

\(\hat X_{fn}\in \mathbb{C}^{M \times M}\)本身也是一个矩阵，是复幅矢量\(x_{fn}\)的协方差矩阵。

\(v_{f n}^{(r)}=\sum_{k=1}^K z_{k r} w_{f k} h_{k n}\)是源\(r\)在该时频单元（可视为时频图上的一个点）的功率。

因此这个过程即为将每个音源的声场模式按照功率分布加权叠加，得到整体声场的二阶统计。

关于复幅矢量\(x_{f n}=\left[X_1(f, n), X_2(f, n), \ldots, X_M(f, n)\right]^{\mathrm{T}} \in \mathbb{C}^M\)，指的是对于指定时间和频率，按通道叠加形成的矢量。

FastMNMF

\(\tilde{X}_{f n}^{-1}=\left(\sum_{k=1}^K w_{f k} h_{k n} Q_{f k}\right)^{-1}\)的计算非常耗时。FastMNMF认为如果矩阵\(Q_{fk}\)都是对角矩阵，将大大减少计算量。但\(Q_{f k}=\sum_{r=1}^R z_{k r} G_{f r}\)，体现不同麦克风之间的相关性，显然很难为对角矩阵。为此，需对\(Q_{fk}\)进行联合对角化：

\[ \left\{\begin{array}{l}Q_{f 1}=\left(P_f^{-1}\right)^{\mathrm{H}} \mathcal{Q}_{f 1} P_f^{-1}, \\\quad \vdots \\Q_{f K}=\left(P_f^{-1}\right)^{\mathrm{H}} \mathcal{Q}_{f K} P_f^{-1},\end{array}\right. \]

这意味着将原本相关的基映射到一组独立的基上去。在迭代过程中，原本的\(X_{f n}, \tilde{X}_{f n}, Q_{f k}, A, B\)全部替换为对角化的\(\mathcal{X}_{f n}, \hat{\mathcal{X}}_{f n}, \mathcal{Q}_{f k}, \mathcal{A}_{f k}, \mathcal{B}_{f k}\)，即使用一组正交的基来分解，并额外估计\(\left[\mathbf{P}_i\right]_m\) ：

\[ \left[\mathbf{P}_i\right]_m \leftarrow\left((1 / J) \sum_{j=1}^J \mathbf{X}_{i j} /\left[\hat{\boldsymbol{x}}_{i j}\right]_{m m}\right)^{-1}\left[\left(\mathbf{P}_i^{-1}\right)^H\right]_m \]

当然如果只是希望分解（比如用于聚类、事件检测等工作），并不需要在映射回原本的基空间。源分解部分也是相同的，有\(\mathcal Q_{f k}=\sum_{r=1}^R z_{k r} \mathcal G_{f r}\)，这时映射回原空间则是必要的。

FastMNMF的改进

上述对SCM的分解认为SCM是满秩的，这与MNMF的满秩空间模型有关，这通常在强回响环境下成立。在弱回响条件下，特别是定向声源条件下，SCM更接近一个秩为1的矩阵。满秩的无约束SCM同一陷入局部最优解且计算开销较大，而独立低秩矩阵分析（independent low-rank matrix annalysis， ILRMA）的秩为1的假设的表示能力有限，通常只能应用于麦克风数等同于扬声器数量的情况。另一方面，MNMF没有显式的空间感知也是其不足之处。在后续的讨论中，使用\(M\)表示麦克风数量，\(N\)表示音源数量。

秩1的空间模型

对于线性混合模型：

\[ \mathbf{x}_{f n}=\sum_{r=1}^N \mathbf{a}_{r f} s_{r f n}, \]

\(a_{rf}\)描述第\(r\)个声源在\(f\)频率下到各个麦克风的幅度响应。

定义“源图像（Source image）”为麦克风接受的对应某一个源的信号：\(\mathbf x_{rfn} = \mathbf a_{rf}s_{rfn}\)。其空间特性矩阵SCM为：

\[ \mathbf{R}_{r f n}=\mathbb{E}\left[\mathbf{x}_{r f n} \mathbf{x}_{r f n}^H\right]=\mathbb{E}\left[\left|s_{r f n}\right|^2\right] \mathbf{a}_{r f} \mathbf{a}_{r f}^H=v_{r f n} \mathbf{a}_{r f} \mathbf{a}_{r f}^H . \]

\(\mathbf{a}_{r f} \mathbf{a}_{r f}^H\)显然是一个秩1矩阵。

源图像的定义引出了一个反思：在我们讨论过的盲源分离方法中，我们的目标是估计源图像还是原始信号？其实根据MNMF的定义，很容易就可以看出我们希望估计的是源图像，因为当我们考虑基信号组合称为“源信号”时，已经默认为“源信号”是应该包括空间混响的。

与MNMF的混合模型最大的差异是源图像向量允许被互不相关的空间分量分解。尽管或许理解上有误，使用基向量的分解方式使得分解从麦克风的接受视角分析信号，例如在某一时刻麦克风可能介绍到了N个音源的信号，和P个回声信号。无论如何，这些信号组成了基信号\(Q_{f k}=\sum_{r=1}^R z_{k r} G_{f r}\)。而某些基信号可能由同一个源贡献。这样的假设即为MNMF的混合模型提供了满秩的可能。

总之，秩1和满秩（或者秩＞1）的情况的直观区别在于源图像是否可以由复数基信号组成，对应物理现象是源图像是否包含多路径。

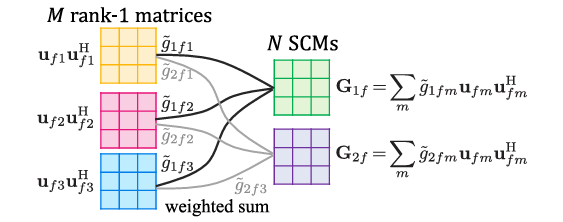
对FastMNMF的新解释：考虑\(G_{f r}=\left(P_f^{-1}\right)^{\mathrm{H}} \mathcal{G}_{f r} P_f^{-1} = \sum_{m = 1}^M\mathcal{G}_{f r m}u_{fm}^{H}u_{fm}\)，使用\(u\)仅是为了简写，可见\(G_{fr}\)是\(M\)个秩1的矩阵的加权和。当\(\mathcal{G}_{f r}\)是一个对角线有且仅有一个非零量（为\(1\)）的矩阵时，FastMNMF退化为秩1空间模型，即退化为ILPMA。

FastMNMF2

考虑\(G_{f r}=\left(P_f^{-1}\right)^{\mathrm{H}} \mathcal{G}_{f r} P_f^{-1} = \sum_{m = 1}^M\mathcal{G}_{f r m}u_{fm}^{H}u_{fm}\)，如果让每一个声源在所有频率上共享方向权重，得到权重共享的可联合对角化满秩空间模型（weight‑shared jointly‑diagonalizable, WJD），则有：

\[ G_{f r}=\left(P_f^{-1}\right)^{\mathrm{H}} \mathcal{G}_{ r} P_f^{-1} = \sum_{m = 1}^M\mathcal{G}_{ r m}u_{fm}^{H}u_{fm} \]

带约束的FastMNMF

\(\mathcal G_f \in \mathbb R^{M\times M}\)的每一行通常代表每个每个音源的空间指向，并且当其中的元素被置\(0\)之后，他们在迭代过程中就会永远保持为\(0\)。如果认为每一个音源都有良好的指向性，可以使用one-hot向量初始化\(\mathcal G_{fr}\)，而漫射音源则可以使用全\(1\)向量初始化。

\[ \mathcal{G}_{ f}=\left(\begin{array}{cccccc}1 & 0 & \ldots & 0 & \ldots & 0 \\0 & 1 & \ldots & 0 & \ldots & 0 \\\vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\0 & 0 & \ldots & 1 & \ldots & 0 \\1 & 1 & \ldots & 1 & \ldots & 1 \\\vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\1 & 1 & \ldots & 1 & \ldots & 1\end{array}\right) . \]

假设有\(L\)个定向源（如说话人）和\(N-L\)个漫射噪音源，则可以将\(\mathcal G\)如上设置。另一方面，如果我有期望增强的目标说话人，也可以通过指定\(u_{f1}\)（\(P^{-1}_{f}\)的第一列）为混合信号经验 SCM 的主特征向量，并将\(\{u_{fm}\}_{m = 2}^{M}\)指定为其他特征向量来将目标说话人保持在分离后的第一个通道。

然后，按照这种假设，如果我们将目标说话人的\(\mathcal G_{fr}\)设置为\((1,0,0,...,0)\)，那么说话人的空间模型将退化为秩1的空间模型，此时其SCM可以写作\(G_{f r}=\sigma_{f r} a_f(\theta) a_f(\theta)^{\mathrm{H}}\)，也就是我们在秩1的空间模型中讨论过的形式。其中\(\theta\)为说话人所在的空间。那么，\(P_f^{-1}\)的第一列，即\(u_{f1}\)一定是\(a_f(\theta)\)。

那么，这个\(a_f(\theta)\)如何得到呢？一般的，\(a_f(\theta)\)可以写作：

\[ a_f[m]=g_m(f) \alpha_m(f) e^{-j k \Delta r_m} \]

其中，\(g_m(f)\)为通道增益，\(\alpha_m(f)\)为幅度因子，\(\Delta r_m\)为相对传播距离。以下是四种情况下的结论：

远场平面波：幅度相同，设第\(m\)振源的几何投影为\(p_m^{\top} u(\theta)\)，有：

\[ a_f(\theta)[m]=g_m(f) \exp \left(-j 2 \pi f \tau_m\right)=g_m(f) \exp \left(-j k p_m^{\top} u(\theta)\right), \quad m=1, \ldots, M . \]
近场球面波：幅度随距离衰减，有：

\[ a_f(\theta)[m]=\frac{g_m(f)}{r_m} \exp \left(-j k r_m\right) \]

均匀直线阵：幅度相同，振幅相同，仅取决于投影。设麦克风之间间距为\(d\)：

\[ a_f(\theta)[m]=\exp \left(-j \frac{2 \pi f}{c} m d \cos \theta\right) \]

因此，结合对波形的假设，存在直接使用\(\theta\)来指定得到的波形的可能。

除此之外似乎也有直接显式引入DOA的NMF方法，之后可能也会研究。

符号

符号	含义
\(f\)	频率索引
\(n\)	时间帧索引
\(k\)	基分量索引
\(r\)	声源索引
\(M\)	麦克风数 (microphones)

符号	含义
\(w_{fk}\)	第 (k) 个基分量在频点 (f) 的功率谱
\(h_{kn}\)	第 (k) 个基分量在时间帧 (n) 的激活强度
\(Q_{fk}\)	第 (k) 个基分量在频点 (f) 的空间协方差
\(z_{kr}\)	声源 (r) 对基分量 (k) 的责任度
\(G_{fr}\)	声源 (r) 在频点 (f) 的空间特性向量
\(\tilde X_{fn}\)	当前模型估计协方差
\(\hat X_{fn}\)	源分离扩展模型协方差