波束形成
波束形成
空间协方差矩阵 SCM
在多麦克风语音处理里,我们把每一个频点 \(f\) 上、在同一时刻 \(t\) 采集到的 \(\mathbf{M}\) 路复数 STFT系列表示为一个列向量:
\[ \mathbf{y}(t, f)=\left[\begin{array}{c} Y_1(t, f) \\ Y_2(t, f) \\ \vdots \\ Y_M(t, f) \end{array}\right] \in \mathbb{C}^{M \times 1} \]
其空间协方差矩阵SCM定义为:
\[ \mathbf{\Phi}(f)=\mathbb{E}\left[\mathbf{y}(t, f) \mathbf{y}(t, f)^{\mathrm{H}}\right] \in \mathbb{C}^{M \times M} \]
有时也需要每一帧的局部SCM:
\[ \hat{\boldsymbol{\Phi}}_y(t, f)=\frac{1}{2 w+1} \sum_{t^{\prime}=t-w}^{t+w} \mathbf{y}\left(t^{\prime}, f\right) \mathbf{y}\left(t^{\prime}, f\right)^{\mathrm{H}} \]
对于一些用于区分说话人和噪音的应用中,也会使用到类似这样的写法:
\[ \begin{aligned}& \hat{\boldsymbol{\Phi}}_s(f)=\frac{\sum_t n(t, f) \mathbf{y}(t, f) \mathbf{y}(t, f)^{\mathrm{H}}}{\sum_t n(t, f)} \\& \hat{\boldsymbol{\Phi}}_n(f)=\frac{\sum_t \xi(t, f) \mathbf{y}(t, f) \mathbf{y}(t, f)^{\mathrm{H}}}{\sum_t \xi(t, f)}\end{aligned} \]
\(n(t,f)\)和\(\xi(t,f)\)分别是说话人软掩码和噪音软掩码。
波束形成
本节中\(l,t\)都代表时间维度,总通道数为\(N\)。
波束形成(beamformer)的一般公式为:
\[ Y_{\mathrm{BF}}(l, f)=\mathbf{w}^T(l, f) \mathbf{x}(l, f), \]
其中\(\mathbf{x}(l, f)=\left[X_0(l, f), X_1(l, f), \ldots, X_{N-1}(l, f)\right]^T,\)\(N\)路麦克风的接受信号,\(\mathbf{w}(l, f)=\left[W_0(l, f), \ldots, W_{N-1}(l, f)\right]^T\) 是复系数。
有时在波束形成后端也会增加一个后滤波器:
\[ Y(l, f)=G(l, f) Y_{\mathrm{BF}}(l, f) \]
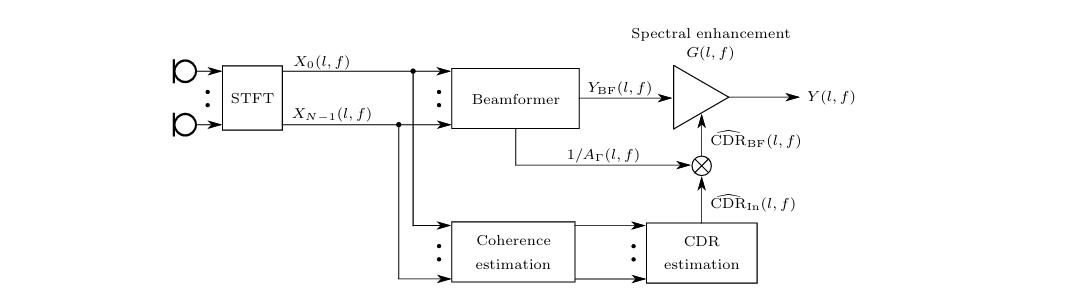
加权延迟-求和波束形成 Weighted DSBF
一种比较简单的波束形成方式是加权延迟-求和波束形成(Weighted delay-and-sum beamformer,Weighted DSBF),其第\(n\)通道的滤波系数被定义为:
\[ W_n(l, f)=w_n(l) e^{-j 2 \pi f \tau_n(l)} \]
考察目标声源到达时间差异,依照平面波模型,流向矢量(steeringn vector)写作:
\[ \mathbf{h}(l, f)=\left[e^{\mathrm{j} 2 \pi f \tau_0(l)}, e^{\mathrm{j} 2 \pi f \tau_1(l)}, \ldots, e^{\mathrm{j} 2 \pi f \tau_{N-1}(l)}\right]^T, \]
其中\(\tau_n(n)=\frac{\mathbf{a}^T(n) \mathbf{p}_m}{c}\)代表第\(m\)麦克风的相对时间时差。\(\mathbf p_m\)代表麦克风\(m\)的笛卡尔坐标,\(\mathbf a(n)\)是从声源指向坐标原点的单位向量:
\[ \mathbf{a}(l)=-\left[\sin \left(\theta_d\right) \cos \left(\phi_d\right), \sin \left(\theta_d\right) \sin \left(\phi_d\right), \cos \left(\theta_d\right)\right]^T \]
每个源接收到的信号可以被建模为:
\[ X_n(l,f) = \sum_{r=1}^N a_{n,r f} s_{n,r lf}, \]
\(a_{rf}\)描述第\(r\)个声源在\(f\)频率下到各个麦克风的幅度响应。为了简化,我们假设仅有两个音源,其余被建模为噪音,则有:
\[ X_n(l,f) = s_{n,1lf}e^{j2\pi f\tau_{1,n}(l)}+s_{n,2lf}e^{j2\pi f\tau_{2,n}(l)} \]
与上述滤波器相乘之后,得到:
\[ Y_{BF}(l,f) = \sum_{n = 0}^{N-1}s_{n,1lf}w_n(l)+\sum_{n = 0}^{N-1}s_{n,2lf}w_n(l)e^{j2\pi f (\tau_{2,n}-\tau_{1,n})} \]
从而增强了目标信号。所以这一过程也被称为时对齐(time-alignment)。
为了获取\(\tau\),除了直接根据位置和平面波假设计算之外,也可以使用广义互相关相位变换 (Generalized Cross-Correlation with Phase Transform, GCC-PHAT)来计算。但这项技术似乎仅在只有一个说话人,或者在固定场景下有已知的说话人片段的情况下可以使用。
简单来说,对于两个通道,其互相关:
\[ R_{12}[\tau]=\sum_n x_1[n] x_2[n+\tau] \]
在\(\tau = \tau_d\)时取最大值。利用卷积定理,互相关可写为傅里叶域乘积的逆变换:
\[ R_{12}[\tau]=\mathcal{F}^{-1}\left\{X_1[k] X_2^*[k]\right\} \]
\(X\)是对\(x\)的离散傅里叶变换的结果,\(*\)代表复共轭。
在计算式,为了提升信噪比,通常会施加一组频域权函数\(G[k]\):
\[ R_{12}^{(G)}[\tau]=\mathcal{F}^{-1}\left\{G[k] X_1[k] X_2^*[k]\right\} . \]
这种互相关则称之为广义互相关。
更进一步的,在这个过程中我们主要关注相位差信息,因此引入PATH权函数:
\[ G_{\mathrm{PHAT}}[k]=\frac{1}{\left|X_1[k] X_2^*[k]\right|} \]
以去除广义互相关计算中的幅度项:
\[ X_1[k] X_2^*[k] G_{\mathrm{PHAT}}[k]=\frac{X_1[k] X_2^*[k]}{\left|X_1[k] X_2^*[k]\right|}=e^{j\left(\phi_1[k]-\phi_2[k]\right)} \]
幅度平方相干 MSC
假设某个时频单元被定向目标语音主导,则该时频单元具有相干性;被漫射噪声或房间混响主导,则表现出非相干性。则可以根据通道间相关性提取一部分特征。通道\(i\)和通道\(j\)之间的相关性可以被写作:
\[ \operatorname{ICC}(i, j, t, f)=\frac{\hat{\Phi}_y(t, f, i, j)}{\sqrt{\hat{\Phi}_y(t, f, i, i) \hat{\Phi}_y(t, f, j, j)}} \]
这种计算方式被称作幅度平方相干(Magnitude Squared Coherence, MSC)。总的幅度平方相干是对每个通道的求和,其中\(P=\frac{M(M-1)}{2}\)代表总的麦克风对数:
\[ \operatorname{MSC}(t, f)=\frac{1}{P} \sum_{i=1}^D \sum_{j=i+1}^D|\operatorname{ICC}(i, j, t, f)| \]
如果假设成立,当某个时频单元在所有通道上都被定向声源强烈主导,则\(MSC\)趋近于\(1\);否则\(MSC\)则类似于sinc函数。MSC在高频段区分度更高,在低频区域容易收到麦克风接收到信号的相位差的影响。
直达与弥散功率比
另一种相干性滤波器则基于空间相关性。定义CDR(coherent-to-diffuse power ratio,直达与弥散功率比):
\[ \operatorname{CDR}(l, f)=\frac{\Gamma_n(l, f)-\Gamma_x(l, f)}{\Gamma_x(l, f)-\Gamma_s(l, f)}, \]
\(\Gamma_x(l, f), \Gamma_s(l, f), \Gamma_n(l, f)\)分别表示观测信号、直达路径信号和噪声在麦克风间的相干函数。直达信号与弥散噪声的空间相干函数分别为:
\[ \begin{aligned}& \Gamma_s(l, f)=e^{\mathrm{j} 2 \pi f\left(\tau_p(l)-\tau_q(l)\right)}, \\& \Gamma_n(f)=\frac{\sin \left(2 \pi f d_{p q}^n / c\right)}{2 \pi f d_{p q}^n / c},\end{aligned} \]
\(d_{pq}^n\)代表两个麦克风之间的间距。sinc的形式是认为弥散噪音声场来自无穷多个各个方向的平面波叠加,对球面方向积分得到的。
观测信号的相关函数由功率谱密度递归得到:
\[ \begin{gathered}\hat{\Gamma}_x(l, f)=\frac{\hat{\Phi}_{x_p x_q}(l, f)}{\sqrt{\hat{\Phi}_{x_p x_p}(l, f) \hat{\Phi}_{x_q x_q}(l, f)}}, \\\hat{\Phi}_{x_p x_q}(l, f)=\lambda \hat{\Phi}_{x_p x_q}(l-1, f)+(1-\lambda) X_p(l, f) X_q^*(l, f),\end{gathered} \]
其中\(\lambda\)是遗忘因子。引入递归可能为了让实测信号更加平稳。
实际使用CDR时往往不会如上计算。因为我们需要一个实值CDR,而上述计算方式很可能给出复值结果。为此需要引入估计器,在这里直接展示:
DOA无关估计器
\[ \begin{aligned}&\widehat{\mathrm{CDR}}_{\text {DOAindep }}=\\&\max \left(0, \frac{\Gamma_{\mathrm{n}} \operatorname{Re}\left\{\hat{\Gamma}_{\mathrm{x}}\right\}-\left|\hat{\Gamma}_{\mathrm{x}}\right|^2-\sqrt{\Gamma_{\mathrm{n}}^2 \operatorname{Re}\left\{\hat{\Gamma}_{\mathrm{x}}\right\}^2-\Gamma_{\mathrm{n}}^2\left|\hat{\Gamma}_{\mathrm{x}}\right|^2+\Gamma_{\mathrm{n}}^2-2 \Gamma_{\mathrm{n}} \operatorname{Re}\left\{\hat{\Gamma}_{\mathrm{x}}\right\}+\left|\hat{\Gamma}_{\mathrm{x}}\right|^2}}{\left|\hat{\Gamma}_{\mathrm{x}}\right|^2-1}\right)\end{aligned} \]
\[ \widehat{\operatorname{CDR}}_{\text {Thiergart }}=\max \left(0, \frac{\operatorname{Re}\left\{\Gamma_n-\hat{\Gamma}_x\right\}}{\hat{\Gamma}_x-e^{\mathrm{j} \arg \hat{\Gamma}_x}}\right) \]
DOA依赖估计器
\[ \overline{\mathrm{CDR}}_{\text {DOAdep }}=\max \left\{0, \frac{1-\Gamma_n \cos \left(\arg \left(\Gamma_s\right)\right)}{\left|\Gamma_n-\Gamma_s\right|}, \frac{\Gamma_s^*\left(\Gamma_n-\hat{\Gamma}_x\right)}{\operatorname{Re}\left\{\Gamma_s^* \hat{\Gamma}_x\right\}-1}\right\} \]
\[ \overline{\mathrm{CDR}}_{\mathrm{Jeub}}=\max \left(0, \frac{\Gamma_n-\operatorname{Re}\left\{\Gamma_s^* \hat{\Gamma}_x\right\}}{\operatorname{Re}\left\{\Gamma_s^* \hat{\Gamma}_x\right\}-1}\right) \]
第一个估计器的特点是不需要计算\(F_s\),因而依赖于空间中仅有一个说话人,事实上整个CDR方法都很依赖这一点,但如第二个估计器这般显式指定总归是能提供一些滤波效果。
计算CDR之后,可以将其应用在后滤波器上:
\[ G(l, f)=\max \left\{1-\mu \frac{1}{1+\operatorname{CDR}(l, f)}, G_{\min }\right\} \]
但如果要这样使用,则需要的是\(Y_{BF}\)的CDR,而非\(X\)的CDR。可以通过引入矫正因子来转换:
\[ \widehat{\mathrm{CDR}}_{\mathrm{BF}}(l, f)=\frac{\widehat{\mathrm{CDR}}_{\mathrm{In}}(l, f)}{A_{\Gamma}(l, f)}, \]
矫正因子被定义为:
\[ A_{\Gamma}(l, f)=\mathbf{w}^H(l, f) J_{\text {diff }}(f) \mathbf{w}(l, f), \]
其中的\(J_{diff}\)是\(N\times N\)的弥散噪音空间相关性矩阵。实际上,矫正因子\(A_{\Gamma}\)反应的是如果输入是单位功率的各向同性扩散场,波束输出端的功率会被放大多少。这里使用\(J_{diff}\)似乎并不意味着\(A_\Gamma\)直接与弥散噪音相关,而是弥散噪音的空间相关性矩阵(把相关性\(\Gamma_n\)重排)本身就是一个各向同性扩散场的空间相关性矩阵:
\[ \left[\mathbf{J}_{\mathrm{diff}}(f)\right]_{p q}=\Gamma_n^{(p q)}(f), \]
多通道语音分离和神经波束形成 MC-SS&Neural Beamforming
传统波束形成的主要缺点在于其主要处理仅存在一个定向信号(说话人)的情况,且对波束形成权重的估计依赖于经验。
考虑,多通道信号中蕴含信息一般体现在时域、频域与空间信息。这些信息通常使用双耳(多麦克风)顺位差(IPD)与根据到达方向(DOA)估计的理论IPD(T-IPD)的相似度提取相关信息。这种方式通常结合短时傅里叶变换实现,并对STFT的窗口大小有所要求。另一种方法则直接使用可学习滤波器直接处理原始信号,但这通常难以利用DOA信息。
基于这些信息,使用神经网络生成权重以进行波束形成的方式被称为神经波束形成。
频域信息通常基于T-F信息(时频图),直接使用神经网络提取。根据神经网路预测目标也可以分:
- 神经网络生成掩码,之后在独立进行波束形成的二阶段框架
- 联合训练波束形成与掩码估计的二阶段框架
- 直接使用神经网路预测波束形成权重
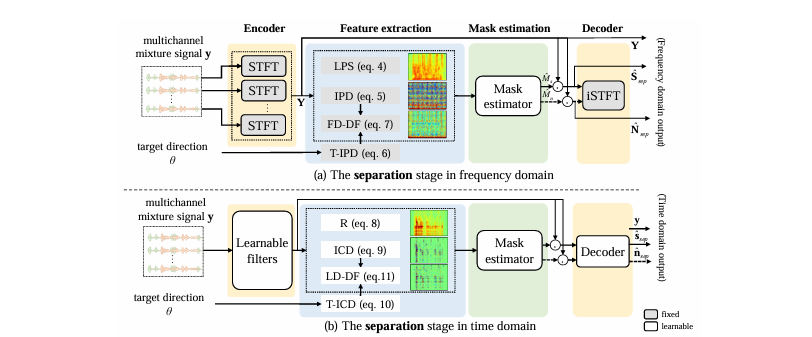
频域方向特征 FD-DF
STFT 可视为将时域信号与指数窗\(w[n]\)的卷积。
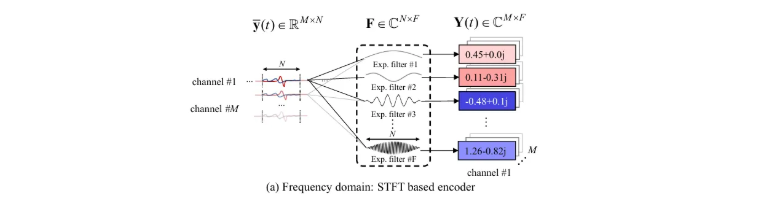
指数窗卷积核可以简单定义为:
\[ F_{n f}=w[n] e^{-j \frac{2 \pi}{N} n f} \]
则STFT的结果为:
\[ Y^{(m)}(t, f)=y^{(m)}(t) \circledast \mathbf{F}_f=\sum_{n=0}^{N-1} y^{(m)}(t H+n) F_{n f} \]
其中\(H\)是帧移。对数功率谱LPS定义为:
\[ \mathrm{LPS}_{t, f}=20 \log _{10}\left|Y^{(\mathrm{ref})}(t, f)\right| \]
表现STFT谱的强度信息,\(ref\)表示参考麦克风。每一对麦克风\(p\)之间的双耳相位差IPD定义为:
\[ \operatorname{IPD}_{t, f}^{(p)}=\angle\left(Y^{(p)}(t, f)\right)-\angle\left(Y^{(\mathrm{ref})}(t, f)\right) . \]
理论相位差与第\(p\)对麦克风之间的几何时延有关,时延可以根据麦克风对之间的距离和DOA来计算:\(\tau^{(p)}(\theta)=d^{(p)} \cos \theta / c\)。由此理论相位差(T-IPD)被定义为:
\[ \begin{aligned}\mathrm{T}-\mathrm{IPD}_{t, f}^{(p)}(\theta)=&\angle\left[\delta[n] \circledast \mathbf{F}_f\right]-\angle\left[\delta\left[n-\tau^{(p)}(\theta)\right] \circledast \mathbf{F}_f\right]\\=&-\frac{2 \pi f}{N} \tau^{(p)}(\theta)\end{aligned} \]
根据\(IPD\)和\(T-IPD\)之间的关系则可以得到频域方向特征(frequency domain directional feature ,FD-DF):
\[ \mathrm{FD}-\mathrm{DF}_{t, f}(\theta)=\sum_p\left\langle\mathrm{IPD}_{t, f}^{(p)}, \mathrm{T}-\mathrm{IPD}_{t, f}^{(p)}(\theta)\right\rangle \]
使用神经网络处理该特征以分离掩码,可以估计目标语音的复比掩码\(\hat M_s\)和干扰语音的复比掩码\(\hat M_n\),也可以估计所有可能说话人的掩码和噪音掩码。这些掩码与多通道混合谱图逐元素相乘则可以起到分离信号的作用。如果STFT的时域窗口大小远大于特征时间(一个周期,通常满足),则可以使掩码对所有通道共享。
潜在域方向特征 LD-DF
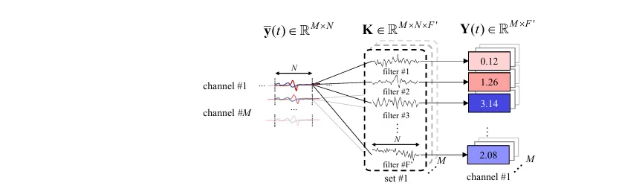
使用可学习窗代替STFT的指数窗:
\[ \mathbf{K}^m=w^m \mathbf{K}^0 \quad(m=1, \ldots, M) \]
其中\(K_0\)是可学习的参考滤波器组,\(w\in \mathbb R^{n}\)是一组可学习权重。使用这组权重计算每对麦克风的特征图卷积差分(ICD):
\[ \mathrm{ICD}_{t, f^{\prime}}^{(p)}=\bar{y}^{\left(p_1\right)}(t) \circledast K_{f^{\prime}}^{\left(p_1\right)}-\bar{y}^{\left(p_2\right)}(t) \circledast K_{f^{\prime}}^{\left(p_2\right)}, \]
同时定义目标ICD:
\[ \mathrm{T}-\mathrm{ICD}_{t, f^{\prime}}^{(p)}(\theta)=\delta[n] \circledast K_{f^{\prime}}^{\left(p_1\right)}-\delta\left[n-\tau^{(p)}(\theta)\right] \circledast K_{f^{\prime}}^{\left(p_2\right)} \]
比较两者,则将得到潜在域方向特征(LD-DF):
\[ \mathrm{LD}-\mathrm{DF}_{t, f^{\prime}}(\theta)=\sum_p\left\langle\mathrm{ICD}_{t, f^{\prime}}^{(p)}, \mathrm{T}-\mathrm{ICD}_{t, f^{\prime}}^{(p)}(\theta)\right\rangle . \]
相比于直接对应几何时延的FD-DF,LD-DF被定义在基于学习的潜在子空间上。网络自己学一套最适合声源分离的潜在滤波器,再与相同滤波器作用下的几何模板比对。
等化最小方差无失真响应(MVDR)闭式解
对于波束形成过程:
\[ Y_{\mathrm{BF}}(l, f)=\mathbf{w}^H(l, f) \mathbf{x}(l, f) \]
希望在方向\(\mathbf{v}(f)\)保持增益同时使得输出残余噪音功率最小。在之前,我们提到了Weighted DSBF方法,而MVDR闭式解是另一种方法。这种方法将上述问题转化为带约束的优化问题:
\[ \begin{array}{ll}\min _{\mathbf{w}(f)} & \mathbf{w}^H(f) \boldsymbol{\Phi}_{n n}(f) \mathbf{w}(f) \\\text { s.t. } & \mathbf{w}^H(f) \mathbf{v}(f)=1\end{array} \]
其中\(\boldsymbol{\Phi}_{n n}(f)\)为噪音和干扰信号的SCM,\(\boldsymbol{\Phi}_{ss}(f)\)为目标信号的SCM。\(\mathbf{v}\)可以直接由显式DOA指定,也可以使用\(PCA\)方法估计:
\[ \mathbf{v}(f)=\underset{\max }{\operatorname{eigvec}}\left(\boldsymbol{\Phi}_{s s}(f)\right) \]
使用拉格朗日乘子法,构造拉格朗日函数:
\[ \mathcal{L}=\mathbf{w}^H \boldsymbol{\Phi}_{n n} \mathbf{w}-\lambda\left(\mathbf{w}^H \mathbf{v}-1\right) \]
将函数对\(\mathbf w\)求导得:
\[ \frac{\partial \mathcal{L}}{\partial \mathbf{w^*}}=0 \Rightarrow \boldsymbol{\Phi}_{n n} \mathbf{w}=\lambda \mathbf{v} \Rightarrow \mathbf{w}=\lambda \boldsymbol{\Phi}_{n n}^{-1} \mathbf{v} \]
带入约束\(\mathbf{w}^H \mathbf{v}=1\)即可得到:
\[ \lambda=\frac{1}{\mathbf{v}^H \boldsymbol{\Phi}_{n n}^{-1} \mathbf{v}} \]
带回,从而解得权重的闭式解:
\[ \mathbf{w}_{\mathrm{FD}-\mathrm{eq}-\mathrm{MVDR}}(l,f)=\frac{\boldsymbol{\Phi}_{n n}^{-1}(l,f) \mathbf{v}(f)}{\mathbf{v}^H(f) \boldsymbol{\Phi}_{n n}^{-1}(l,f) \mathbf{v}(f)} \]
时域波束形成
另一种波束形成方法则不使用短时傅里叶变换,而是基于时域信息。在计算过程中同样使用的是MVDR闭式解:
\[ \mathbf{w}_{\mathrm{TD}-\mathrm{eq}-\mathrm{MVDR}}=\frac{\mathbf{R}_{n n}^{-1} \mathbf{h}}{\mathbf{h}^T \mathbf{R}_{n n}^{-1} \mathbf{h}} \mathbf{u}, \]
其区别在于\(\mathbf h\)和\(\mathbf R\)的定义:
- \(\mathbf{R}_{s s}=E\left[s(k) s(k)^T\right]\)是目标语音空间相关矩阵
- \(\mathbf{R}_{n n}=E\left[n(k) n(k)^T\right]\)是干扰和噪音的空间相关矩阵
- \(\mathbf h\)是目标方向的导向矩阵
- \(\mathbf u\)是onehot向量,用于区分通道
在实际计算过程中,一般使用目标语音和噪音的估计值计算:
\[ \begin{aligned}\mathbf{R}_{s s}(t, n) & =\hat{s}_{\mathrm{sep}}(t, n) \hat{s}_{\mathrm{sep}}(t, n)^T \\\mathbf{R}_{n n}(t, n) & =\hat{n}_{\mathrm{sep}}(t, n) \hat{n}_{\mathrm{sep}}(t, n)^T\end{aligned} \]
其中\(t\)代表帧数,\(n\)代表采样点。
这两种权重矩阵也可以通过神经网络得到:
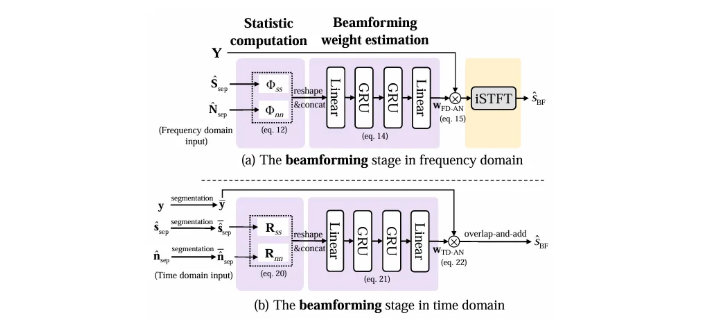
参考
Model-Based Expectation-Maximization Source Separation and Localization
MULTI-CHANNELOVERLAPPEDSPEECHRECOGNITIONWITHLOCATIONGUIDED SPEECHEXTRACTIONNETWORK
MULTI-CHANNEL MULTI-SPEAKER ASR USING 3D SPATIAL FEATURE
Temporal-Spatial Neural Filter: Direction Informed End-to-End Multi-channel Target Speech Separation
Towards Unified All-Neural Beamforming for Time and Frequency Domain Speech Separation






