NMF及语音分离

这一部分在之前的笔记中曾经有过讨论，在这里重新整理，补充缺失的内容。

非负矩阵分解 NMF基本原理

数据通常表示为矩阵形式：

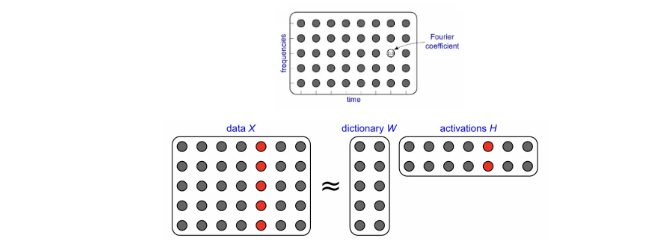
字典学习，低秩近似，因子分析，潜在语义分析等方法，通常会将/将矩阵分解为字典矩阵和行为矩阵的乘积，以实现降维，拆分（源分离），插值等工作。

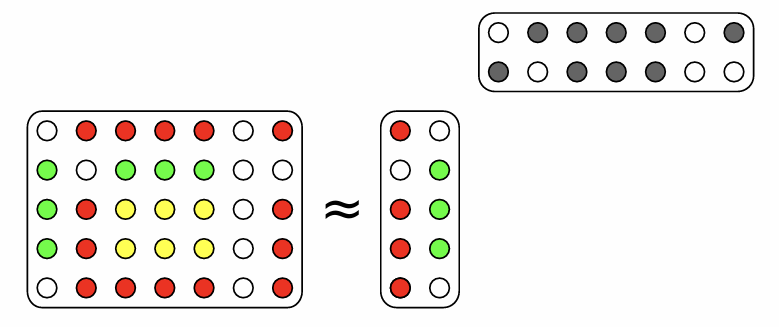
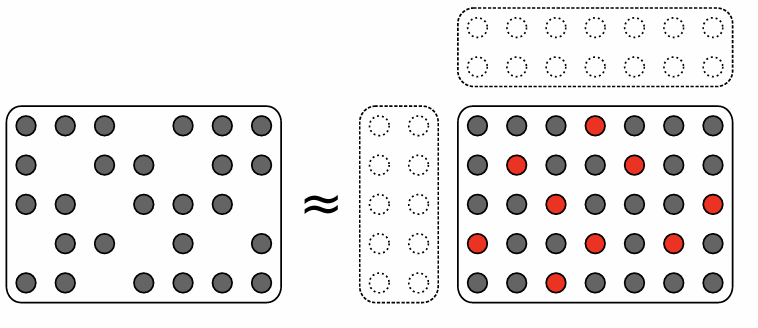
非负矩阵分解要求：

数据 \(V\) 以及因子 \(W,H\) 具有非负的值。

因子 \(W\) 的非负性确保了字典的可解释性，因为模式 \(w_k\) 和样本 \(v_n\) 属于相同的空间。
因子 \(H\) 的非负性倾向于生成基于局部特征的表示，因为禁止使用减法组合。

具体来说，给定一个\(F\times N\)的非负矩阵\(V\)，寻求分解：

\[ V \simeq WH \]

其中，\(W \in \mathbb{R}_{+}^{F \times K}, H \in \mathbb{R}_{+}^{K \times N}\)。选择\(FK+KN\ll FN\)，以实现降维的目的。

NMF的优化

\(W\)和\(H\)通常由优化得来，具体来说，我们选择\(WH\)，以最小化：

\[ \min _{\mathbf{W}, \mathbf{H} \geq \mathbf{0}} D(\mathbf{V} \mid \mathbf{W H})=\sum_{f n} d\left([\mathbf{V}]_{f n} \mid[\mathbf{W H}]_{f n}\right), \]

其中，\(d\)是一个标量损失函数。

一种常用的选择是\(\beta\)散度：

\[ d_\beta(x \mid y) \stackrel{\text { def }}{=}\left\{\begin{array}{cl}\frac{1}{\beta(\beta-1)}\left(x^\beta+(\beta-1) y^\beta-\beta x y^{\beta-1}\right) & \beta \in \mathbb{R} \backslash\{0,1\} \\x \log \frac{x}{y}+(y-x) & \beta=1 \\\frac{x}{y}-\log \frac{x}{y}-1 & \beta=0\end{array}\right. \]

散度在\(\beta = 0\)时是IS散度，\(\beta = 1\)时是\(KL\)散度，\(\beta = 2\)时是欧拉散度。

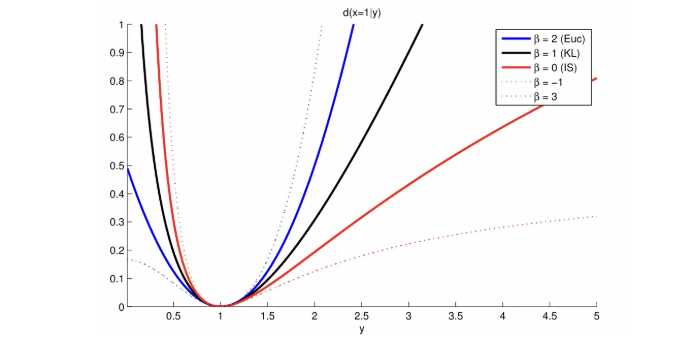
\(\beta\)的不同取值对应了不同的散度形式

平方欧几里得距离 / 二次损失（\(β=2\)）
广义 Kullback-Leibler（KL）散度（\(β=1\)）
Itakura-Saito（IS）散度（\(β=0\)）

性质

齐次性：\(d_\beta(\lambda x \| \lambda y)=\lambda^\beta d_\beta(x \| y)\)
\(d_{\beta}(x||y)\) 是 \(y\) 的凸函数，当 \(1≤β≤2\) 时成立

IS散度，是Itakura和Saito基于短时语音谱最大似然估计推导出的，用于度量两个频谱之间的拟合程度的散度，具有良好的听觉效果。IS散度具有以下特点：

尺度不变性（scale invariance）：高低能量的谱分量具有相同的重要性；
特别适合动态范围大的数据，如短时音频谱；
具备明确的统计解释：对应于叠加信号中 W 和 H 的最大似然估计，在 Gamma 噪声下亦可解释；
可采用乘法更新规则（如 Dhillon 和 Sra 的方法），但其理论收敛性仍未完全证明。

乘法更新规则：

Lee和Seung证明，在\(\beta = 1,2\)时，如以下规则的更新可以使得代价函数下降：

\[ \begin{aligned}& H \leftarrow H \cdot \frac{W^{\top}\left((W H)^{\beta-2} \odot V\right)}{W^{\top}(W H)^{\beta-1}} \\& W \leftarrow W \cdot \frac{\left((W H)^{\beta-2} \odot V\right) H^{\top}}{(W H)^{\beta-1} H^{\top}}\end{aligned} \]

而后对于Bregman散度家族，即通式为：\(d_\phi(x \mid y)=\phi(x)-\phi(y)-\nabla \phi(y)(x-y)\)的散度家族，Dhillon和Sra提出了以下更新规则：

\[ \begin{aligned} & H \leftarrow H \cdot \frac{W^{\top}\left(\nabla^2 \phi(W H) \odot V\right)}{W^{\top}\left(\nabla^2 \phi(W H) \odot W H\right)} \\ & W \leftarrow W \cdot \frac{\left(\nabla^2 \phi(W H) \odot V\right) H^{\top}}{\left(\nabla^2 \phi(W H) \odot W H\right) H^{\top}} \end{aligned} \]

在实践中，IS散度应用以上规则表现出收敛趋势，但无收敛性证明。

尺度不变性

\(\beta\)散度满足\(d_\beta(\gamma x \mid \gamma y)=\gamma^\beta d_\beta(x \mid y)\)，因而在\(\beta = 0\)时，散度是尺度不变的，矩阵的高值和低值具有相同的权重，拟合误差不会因为分量大小而有精度上的区别。

IS-NMF的语音建模

在进一步讨论之前，我们来看一个简单的正弦信号的分离问题。待分离信号如下

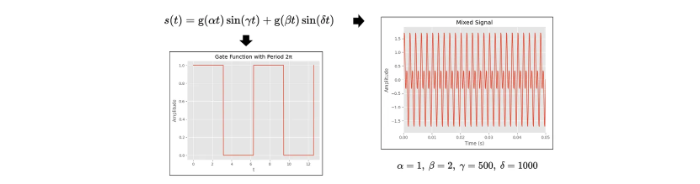
首先我们计算时频图，如图可见时频图高度冗余。对时频图进行NMF计算，得到的W和H两个矩阵。

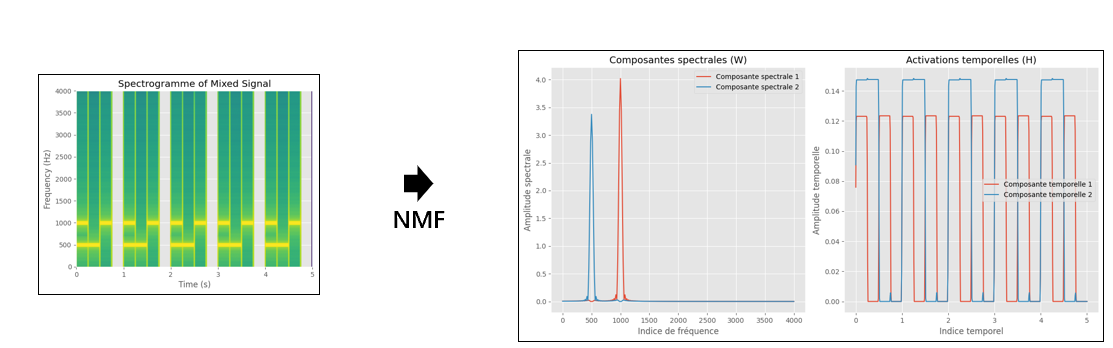
从结果来看分离后的\(W\)和\(H\)分别包含了两个主模式的频率和时间信息。分别称其为频谱基和时间激活。将\(W\)和\(H\)的对应行列再度相乘，得到两个重构的时频图，并所ISTFT可以得到两个分离的信号。

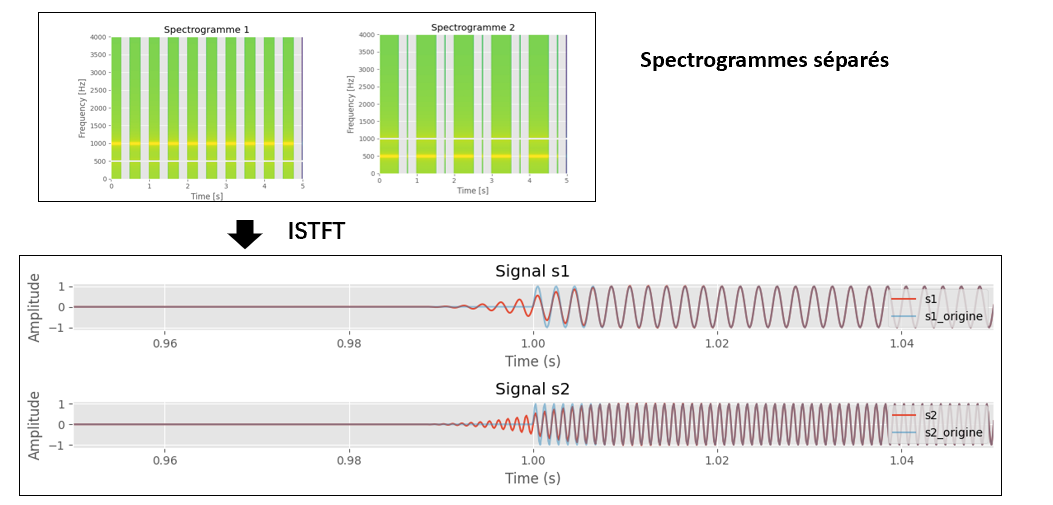
在基础NMF中，接收到的信号被认为是一系列独立随机向量（声源）的线性组合。

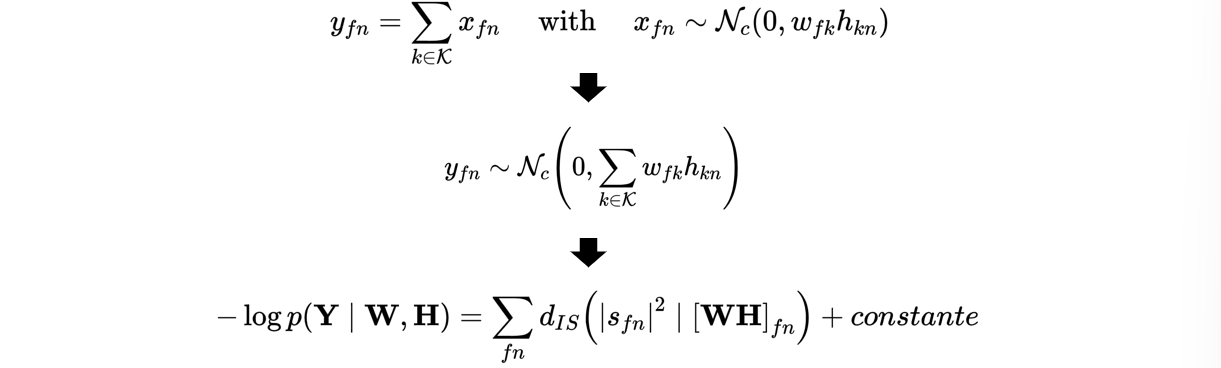
这个建模方法过于简单，多数声源的信号不能被简单的表示为一个随机变量，一个随机变量中包含的信息也常不足以重构一个信号。

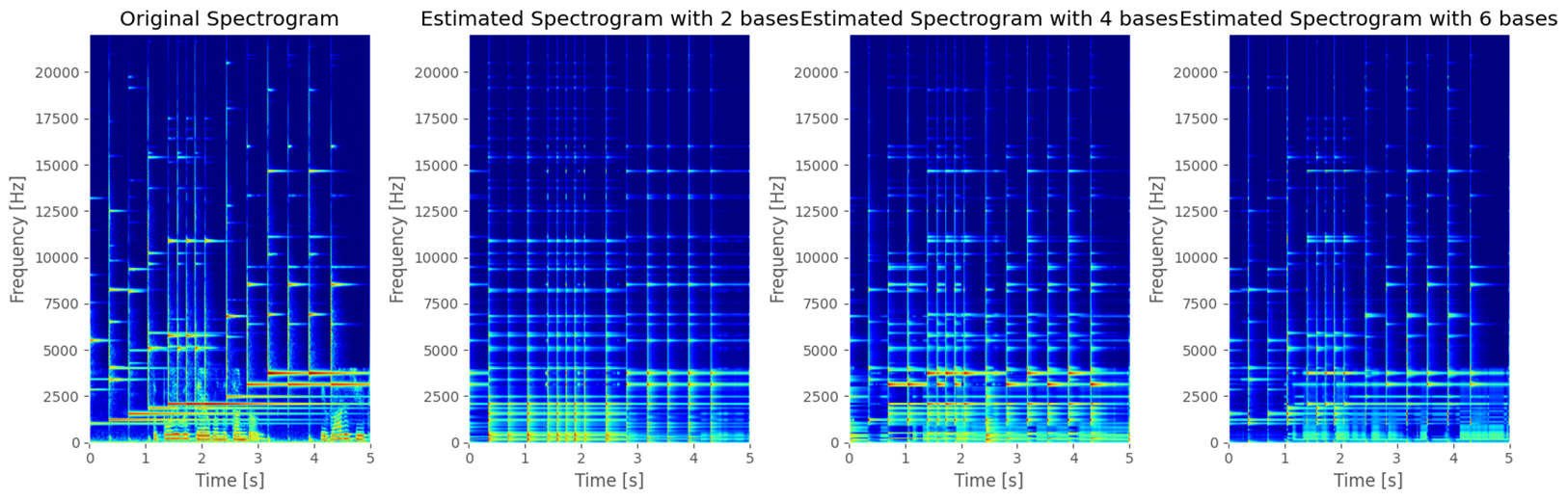
可以看到上图随着使用的基的数量的增加，重构信号逐渐接近于原始信号。而实际上原始信号仅是双信号的叠加。

接下来关注IS-NMF的语音建模。约定原矩阵为\(V\)，其中的元素记作\(v_{fn}\)。分解后，重构矩阵\(\hat V = WH\)。对于列向量，使用小写加粗字体表示，如\(W = [\mathbf w_1, \mathbf w_2,...,\mathbf w_K]\)表示；对于行向量，使用普通小写字母表示，如\(H = [h_1^T,h_2^T,...,h_K^T]^T\)。

IS-NMF 作为高斯分量求和模型的最大似然估计

考虑生成模型：

\[ \mathbf{x}_n=\sum_{k=1}^K \mathbf{c}_{k, n}, \]

其中\(\mathbf{x}_n=\sum_{k=1}^K c_{k, n},\) 且\(c_{k, n} \sim \mathcal{N}_c\left(0, h_{k n} \operatorname{diag}\left(\mathbf{w}_k\right)\right),\) 满足多元高斯分布。假设\(c_{kn}\)\(c_{fn}\)\(x_{fn}\)条件独立，且\(x_{fn}\sim \mathcal{N}_c\left(0, h_{k n} \operatorname{diag}\left(\mathbf{w}_k\right)\right)\)。记\(v_{fn} = |x_{fn}|^2\)。则从矩阵\(X\)最大似然估计得到的\(W\)和\(H\)等价于对\(V\)做以IS散度作为代价函数的非负矩阵分解。

\[ \begin{aligned}C_{M L, 1}(\mathbf{W}, \mathbf{H}) & =-\sum_{n=1}^N \sum_{f=1}^F \log \mathcal{N}_c\left(x_{f n} \mid 0, \sum_k w_{f k} h_{k n}\right) \\& =N F \log \pi+\sum_{n=1}^N \sum_{f=1}^F \log \left(\sum_k w_{f k} h_{k n}\right)+\frac{\left|x_{f n}\right|^2}{\left(\sum_k w_{f k} h_{k n}\right)} \\& \stackrel{\mathrm{c}}{=} \sum_{n=1}^N \sum_{f=1}^F d_{I S}\left(\left|x_{f n}\right|^2 \mid \sum_k w_{f k} h_{k n}\right)\end{aligned} \]

复高斯分布的一维对数密度：

\[ \log \mathcal{N}_c(x \mid \mu, \lambda)=-\log (\pi \lambda)-\frac{|x-\mu|^2}{\lambda} \]

在音频信号的情况下

对于每一个音源（这里假设有两路），各音源的STFT可以表示为：

\[ s_{1, n}=\sum_{k=1}^{K_1} c_{k, n}, \quad s_{2, n}=\sum_{k=K_1+1}^{K_1+K_2} c_{k, n}, \quad \text { avec } K_1+K_2=K . \]

而接受的音频信号的STFT可以被表示为\(\mathbf x_n =\mathbf s_{1,n}+\mathbf s_{2,n}\)。在\(\mathbf x_n = [x_{1,n}, x_{2,n},...,x_{Fn}]\)中，帧率列\(n = 1,...,N\)，频率索引\(f = 1,...，F\)。与之前的简单建模不同，每一音源的STFT被奸魔为若干元素性分量。每个分量具有功率谱密度（PSD）\(\mathbf w_k\)，并由随帧变化的激活系数\(h_{kn}\)在时间上调制。

传统的方法可能会现在训练数据上学习PSD，在将混合信号的谱图\(|X|^2\)进行分解到已知的字典：

\[ W=\left[\mathbf w_1, \ldots, \mathbf w_{K_1}, \mathbf w_{K_1+1}, \ldots, \mathbf w_{K_1+K_2}\right] \]

利用最大似然估计和IS-NMF的相关关系，可以不预先进行估计。

定性的，矩阵外积\(\mathbf w_k\mathbf h_k^T\)在二维坐标中呈现行向量×列向量的结构，而对于时频图：

行向量只随频率变化，因而\(\mathbf w_k\)将仅能提取频率变化信息，因而能够提取频率模板；

列向量只随时间变化，因而\(\mathbf h_k\)将仅能提取时间信息，因而能提取时间包络信息

额外的，对于给定\(W\)和\(H\)，可以通过维纳滤波得到最小均方误差估计，从而实现对信号的分解：

\[ \hat{c}_{k, f n}=\frac{w_{f k} h_{k n}}{\sum_{l=1}^K w_{f l} h_{l n}} x_{f n} \]

对于固定的\((f,n)\)，维纳增益之和为1，分解能量守恒。

考虑\({c_{k,fn}}\)与\(x_{fn}\)的联合分布。两者都复高斯分布，因而联合分布仍未多元复高斯分布：

\[ \begin{aligned} &\left[\begin{array}{c} c_{f n} \\ x_{f n} \end{array}\right] \sim \mathcal{N}_c(0, \underbrace{\left[\begin{array}{cc} \operatorname{diag}\left(\sigma_{f n}^2\right) & \sigma_{f n}^2 \\ \sigma_{f n}^{22} & \lambda_{f n} \end{array}\right]}_{\Sigma_{f n}}),\\ &\text { avec } \sigma_{f n}^2=\left[\sigma_{1, f n}^2, \ldots, \sigma_{K, f n}^2\right]^{\top}, \lambda_{f n}=\sum_k \sigma_{k, f n}^2 \text {. } \end{aligned} \]

对于多元复高斯分布，其条件分布\(z|y\)仍为复高斯分布，其均值和方差分别为：

\[ \mathbb{E}[\mathbf{z} \mid y]=\boldsymbol{\Sigma}_{z y} \boldsymbol{\Sigma}_{y y}^{-1} y, \quad \operatorname{Cov}[\mathbf{z} \mid y]=\boldsymbol{\Sigma}_{z z}-\boldsymbol{\Sigma}_{z y} \boldsymbol{\Sigma}_{y y}^{-1} \boldsymbol{\Sigma}_{y z} . \]

因而考虑后验分布\(c_{k,fn}|x_{fn}\)，有后验均值和后验方差：

\[ \begin{aligned}&\mathbb E[c_{k,fn}\mid x_{fn} ]=\frac{\sigma_{k, f n}^2}{\lambda_{f n}} x_{f n}=\frac{w_{f k} h_{k n}}{\sum_l w_{f l} h_{l n}} x_{f n}\\& \operatorname{Var}\left[c_{k, f n} \mid x_{f n}\right]=\sigma_{k, f n}^2-\frac{\left(\sigma_{k, f n}^2\right)^2}{\lambda_{f n}}=w_{f k} h_{k n}-\frac{\left(w_{f k} h_{k n}\right)^2}{\sum_l w_{f l} h_{l n}} \end{aligned} \]

Wiener滤波方法期望在最小均方误差的准则下，从观测信号中恢复出原始信号。即期望找到一个函数，使得在给定观测\(x\)的条件下，使得条件均方误差：

\[ \operatorname{MSE}(x)=\mathbb{E}\left[|c-\hat{c}(x)|^2 \mid x\right] \]

最小。使用后验均值\(m(x) = \mathbb E[c\mid x]\)（条件期望）表示分解MSE。

\[ E\left[(c-\hat{c}(x))^2 \mid x\right]=E\left[(c-m(x))^2 \mid x\right]+(m(x)-\hat{c}(x))^2, \]

第一项是定值，而第二项仅在\(\hat c = m\)时为零。因此MMSE最小时应有\(\mathbb E[c_{k,fn}\mid x_{fn} ]=\hat{c}_{k, f n}\)。

因而得到上式。

由此式实现音源信号的重构。

乘性噪音

对于生成模型，\(V = (WH) \odot E\)。设\(E\)时均值为\(1\)的独立同分布乘性Gamma噪音。则对\(W,H\)做最大似然估计，等价于将\(V\)分解为\(V = WH\)，代价函数采用IS散度。

上定理在此不再证明。若实际噪声确实近似乘性且服从 Gamma（或更一般的、均值为 1 的乘性分布），则 IS-NMF 的代价函数就是该噪声模型下的负对数似然。

多通道非负矩阵分解 MNMF

IS-NMF解决了基础NMF中的语音建模问题，而只能处理单通道数据的问题则再MNMF中得到了解决。。为此，一种解决方法是多通道非负矩阵分解（Multichannel Nonnegative Matrix Factorization，MNMF）。

MNMF的基本原理

考虑第\(i\in\{1,\ldots,I\}\)个观测通道的采样信号为：

\[ \tilde{x}_i(t)=\sum_{j=1}^J \sum_{\tau=0}^{L-1} \tilde{a}_{i j}(\tau) \tilde{s}_j(t-\tau)+\tilde{b}_i(t) \]

其中，\(\tilde{a}_{i j}(\tau)\)是因果的脉冲响应，\(\tilde{b}_i(t)\)是加性噪音，\(\tilde s_j\)是第\(j\)个源的时域信号。即每个麦克风包含的信号不仅包含声音的直接路径，还包含回波信号。在短时傅里叶变换域中表示为：

\[ x_{i, f n}=\sum_{j=1}^J a_{i j, f} s_{j, f n}+b_{i, f n}\Leftrightarrow \mathbf{X}_{f n}=\mathbf{A}_f \mathbf{S}_{f n}+\mathbf{b}_{f n} \]

研究期望将源的功率谱图分解为两个非负矩阵的乘积\(|S_{fn}|^2\simeq W_{fn}H_{fn}\)，由此系统转化为在给定观察\(X_{fn}\)的情况下，联合估计源谱因子\(\{W_{fn},H_{fn}\}\)和混合矩阵\(A_{fn}\)。

MNMF的音频建模

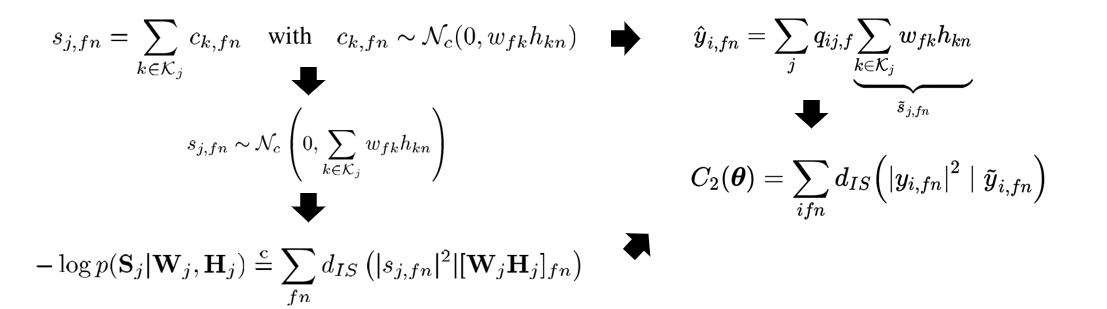
与IS-NMF相同，MNMF认为一个音源\(s_{jfn}\)由多个表现为复高斯分布的成分\(c_{kfn}\)组成。假设\(K\ge J\)，且\(\left\{\mathcal{K}_j\right\}_{j=1}^J\)是\(\mathcal K = \{1,\ldots,K\}\)的一个非平凡划分。认为第\(j\)的音源是\(\# \mathcal K_j\)个潜在成分的总和。

\[ s_{j f n}=\sum_{k \in \mathcal{K}_j} c_{k f n} \quad \text { avec } c_{k f n} \sim \mathcal{N}_{\mathbb{C}}\left(0, w_{f k} h_{k n}\right) \]

成分互相独立，因此有：

\[ s_{j f n} \sim \mathcal{N}_{\mathbb{C}}\left(0, \sum_{k \in \mathcal{K}_j} w_{f k} h_{k n}\right) \]

由IS-NMF的证明，给定源\(S_j = [s_{jfn}]_{fn}\)，最大似然估计\(W_j\)和\(H_j\)等价于将\(|S_j|^2\)分解为\(W_jH_j\)。

\[ -\log p\left(\mathbf{S}_j \mid \mathbf{W}_j, \mathbf{H}_j\right) \cong \sum_{f n} d_{I S}\left(\left|s_{j f n}\right|^2 \|\left[\mathbf{W}_j \mathbf{H}_j\right]_{f n}\right) \]

由于对成分的假设，成分是“有限”且“可重复的”，即不同音源可能包含相同的成分，而总的成分数量小于\(K\)。因此，可以将混合模型重新写作：

\[ \mathbf{x}_{f n}=\mathbf{A}_f \mathbf{c}_{f n}+\mathbf{b}_{f n} \]

其中，\(\mathbf{c}_{f n}=\left[c_{1, f n}, \ldots, c_{K, f n}\right]^{\top} \in \mathbb{C}^{K \times 1}\)为有限种成分。因此，模型被简化作一个有\(I\)个通道和\(K\)个高思远的线性混合模型。记\(\boldsymbol{\Sigma}_{c, f n}=\operatorname{diag}\left(\left[w_{f k} h_{k n}\right]\right)\)。

噪音被假设为平稳且空间上不相关的：

\[ b_{i f n} \sim \mathcal{N}_{\mathbb{C}}\left(0, \sigma_{i, f}^2\right) \]

噪音成分除了模拟常规意义上的噪音之外，同样有利于解释模型不匹配和量化带来的“噪音”。因此引入此噪音对避免数据不稳定性和加速收敛是有必要。记\(\boldsymbol{\Sigma}_{b, f}=\operatorname{diag}\left(\left[\sigma_{i, f}^2\right]_i\right)\)。

NMNF的优化方法

在当前建模下，所有参数包括\(\boldsymbol{\theta}=\left\{\mathbf{A}, \mathbf{W}, \mathbf{H}, \boldsymbol{\Sigma}_b\right\}\)。根据之前的假设， \(x_{fn}\)是一个零均值的复高斯变量，协方差为：

\[ \boldsymbol{\Sigma}_{x, f n}(\boldsymbol{\theta})=\mathbf{A}_f \boldsymbol{\Sigma}_{s, f n} \mathbf{A}_f^H+\boldsymbol{\Sigma}_{b, f} \]

\(\Sigma_{s,fn}\)是源的协方差矩阵。此时，最大似然估计等价于最小化：

\[ \mathcal{C}_1(\boldsymbol{\theta})=\sum_{f n} \operatorname{trace}\left(\mathbf{x}_{f n} \mathbf{x}_{f n}^H \boldsymbol{\Sigma}_{x, f n}^{-1}\right)+\log \operatorname{det} \boldsymbol{\Sigma}_{x, f n} \]

\(x_{fn}\)条件概率密度函数可以写作：

\[ p\left(x_{f n} \mid \theta\right)=\frac{1}{\pi^I \operatorname{det}\left(\Sigma_{x, f n}\right)} \exp \left(-x_{f n}^{\mathrm{H}} \Sigma_{x, f n}^{-1} x_{f n}\right) . \]

负对数似然即为：

\[ \mathcal{L}(\theta)=\sum_{f, n}\left[x_{f n}^{\mathrm{H}} \Sigma_{x, f n}^{-1} x_{f n}+\log \operatorname{det}\left(\Sigma_{x, f n}\right)+I \log \pi\right] \]

最后一项为常数，可以忽略。将二次型写作迹形式，即可得到上式。

在优化中，通常施加\(\sum_i\left|a_{i j, f}\right|^2=1\)，且\(\sum_j w_{f k}=1\)的约束以减少不确定性。这些约束使得\(A_f\)的列对通道归一化，\(W\)的列对频率归一化，幅值信息保留在\(H\)中随时间变化。