Kalman滤波:线性卡尔曼滤波,扩展卡尔曼滤波,无迹卡尔曼滤波
Kalman滤波:线性卡尔曼滤波,扩展卡尔曼滤波,无迹卡尔曼滤波
部分公式为使用标准写法。
Introduction
滤波是在对系统可观测信号进⾏测量的基础上,根据⼀定的滤波准则,采⽤某种统计量最优⽅法,对系统的状态进⾏估计的理论和⽅法。讲点的滤波理论包括维纳(Wiener)滤波和卡尔曼(Kalman)滤波。前者使用频域方法,后者使用时域状态空间方法。
相比于Wiener滤波方法,Kalman滤波只基于时域中的量,不仅可以对平稳的一维随机过程进行估计,也可以对非平稳的、多维随机过程进行估计,同时Kalman滤波算法是递推的,便于在计算机上实现实时应用。
最早Kalman提出的滤波理论只适用于线性系统,此后研究者将其扩展到非线性系统下。其中扩展Kalman滤波(EKF)将非线性系统一阶线性化,再利用Kalman滤波。其问题在于线性化过程中产生的误差。无迹Kalman滤波(UKF)以UT变换处理均值和协方差的非线性传递,计算经济较高。除此之外,为了提升计算效率,平方根滤波和UD分解滤波也逐渐被提出。,
线性Kalman滤波
射影定理
由\(m\times1\)维随机向量\(\mathbf y \in \mathbb R^ m\)的线性函数估计\(n\times 1\)维的随机变量\(\mathbf x \in \mathbb R^n\),记估计值为:
\[ \hat{\mathbf{x}}=\mathbf{b}+\mathbf{A} \mathbf{y}, \mathbf{b} \in \mathbb R^n, \mathbf{A} \in \mathbb R^{n \times m} \]
设最小化性能指标为\(J = \mathrm E((\mathbf x-\hat{\mathbf{x}})^T(\mathbf x-\hat{\mathbf{x}}))\),称\(\hat{\mathbf{x}}\)为\(\mathbf x\)的线性最小方差估计。
此时,线性最小方差估计的表达式为:
\[ \hat{\mathbf x}=\mathrm{E} \mathbf x+\operatorname{Cov}(\mathbf x,\mathbf y) \operatorname{Var}(\mathbf y)^{-1}(y-\mathrm{E}\mathbf y) \]
证明: 对\(\mathbf b\)求偏导并令其为零:
\[ \frac{\partial J}{\partial b}=-2 E[x-A y-b]=0 \quad \Longrightarrow \quad E[x]-A E[y]-b=0 \]
得:
\[ b=E[x]-A E[y] \]
对\(\mathbf A\)求偏导并令其为零:
\[ \frac{\partial J}{\partial A}=-2 E\left[(x-A y-b) y^T\right]=0 \quad \Longrightarrow \quad E\left[x y^T\right]-A E\left[y y^T\right]-b E[y]^T=0 \]
带入\(b = E[x]-AE[y]\),同时根据协方差和方差定义:
\[ \operatorname{Cov}(x, y)=E\left[x y^T\right]-E[x] E[y]^T, \quad \operatorname{Var}(y)=E\left[y y^T\right]-E[y] E[y]^T, \]
得到:
\[ \operatorname{Cov}(x, y)-A\mathrm{Var}(y) = 0\Rightarrow A =\operatorname{Cov}(x, y) \mathrm{Var}(y)^{-1}. \]
合并结果得到:
\[ \hat{x}=\mathrm{E} x+\operatorname{Cov}(x, y) \operatorname{Var}(y)^{-1}(y-\mathrm{E} y) \]
估计\(\hat x\)有以下性质:
- 无偏性, \(E \hat x = E x\)
- 正交性,\(E((x-\hat x)t^T) = 0\)
- \(x-\hat x\)和\(y\)是不相关的随机变量,称\(x-\hat x\)和\(y\)正交,记作\(x-\hat{x} \perp y\)。同时称\(\hat x\)是\(x\)在\(y\)上的投影,记作\(\hat{x}=\operatorname{proj}(x \mid y)\)。
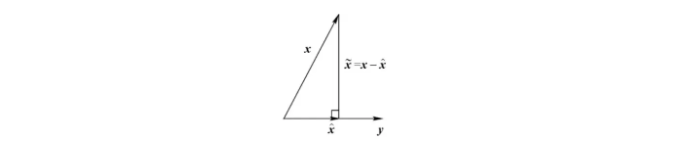
给定随机变量组\(y(1), y(2), \ldots, y(k) \in \mathbb{R}^m\),他们生成的线性流型(Linear Manifold)\(L(y(1), \ldots, y(k))\)定义为:
\[ L(w) = L(y(1), \ldots, y(k))=\left\{A_1 y(1)+A_2 y(2)+\cdots+A_k y(k)+b \mid A_i \in \mathbb{R}^{n \times m}, b \in \mathbb{R}^n\right\} . \]
此时随机向量\(x\)的线性最小估计\(\hat x\)定义为:
\[ \hat{x}=\operatorname{proj}(x \mid w) \triangleq \operatorname{proj}(x \mid y(1), y(2), \cdots, y(k)) \]
称\(\hat x\)是\(x\)在线性流型\(L(w)\)上的投影。
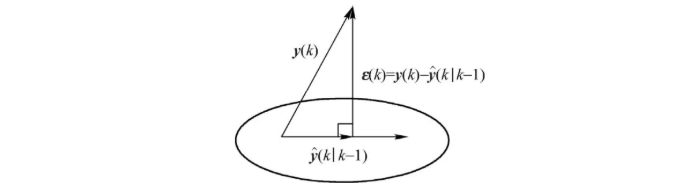
对于存在二阶矩的随机序列\(y(1), y(2), \ldots, y(k) \in \mathbb{R}^m\),定义新息序列\({\mathbf{ \varepsilon}(k)}\):
\[ \varepsilon(k)=y(k)-\operatorname{proj}(y(k) \mid y(1), y(2), \cdots, y(k-1)), \quad k=1,2, \cdots \]
并定义\(y(k)\)的一组最有预报估值为:
\[ \hat{y}(k \mid k-1)=\operatorname{proj}(y(k) \mid y(1), y(2), \cdots, y(k-1)) \]
将新息序列定义写作:
\[ \varepsilon(k)=y(k)-\hat{y}(k \mid k-1), \quad k=1,2, \cdots \]
并规定\(\hat y(1|0) = E(y(1))\),以保证\({\mathbf{ \varepsilon}(1)} = 0\)。
由此,可以得到推论:
\[ \operatorname{proj}(\boldsymbol{x} \mid \boldsymbol{y}(1), \boldsymbol{y}(2), \cdots, \boldsymbol{y}(k))=\operatorname{proj}(\boldsymbol{x} \mid \boldsymbol \varepsilon(1), \boldsymbol \varepsilon(2), \cdots, \boldsymbol \varepsilon(k)) \]
投影运算仅依赖于目标子空间本身,而与生成它的基底或新息序列无关。因此只要证明子空间\(L_y=L(y(1), \ldots, y(k))\)与\(L_{\varepsilon}=L(\varepsilon(1), \ldots, \varepsilon(k))\)等价即可证明上式。
递推射影定理
对于随机变量\(\mathbf x\in \mathbb R^n\),随机序列\(\mathbf y(1),\mathbf y(2),...,\mathbf y(k)\in \mathbb R^m\),且他们都存在二阶矩,则有递推射影公式:
\[ \begin{aligned} \operatorname{proj}(\boldsymbol{x} \mid \boldsymbol{y}(1), \boldsymbol{y}(2), \cdots, \boldsymbol{y}(k))= & \operatorname{proj}(\boldsymbol{x} \mid \boldsymbol{y}(1), \boldsymbol{y}(2), \cdots, \boldsymbol{y}(k-1))+ \\ & \mathrm{E}\left[\boldsymbol{x} \varepsilon^{\mathrm{T}}(k)\right]\left[\mathrm{E}\left(\varepsilon(k) \varepsilon^{\mathrm{T}}(k)\right)\right]^{-1} \varepsilon(k) \end{aligned} \]
首先应用线性最小方差投影公式:
\[ \hat{\mathbf x}=\mathrm{E} \mathbf x+\operatorname{Cov}(\mathbf x,\mathbf \varepsilon) \operatorname{Var}(\mathbf \varepsilon)^{-1}(\varepsilon-\mathrm{E}\mathbf \varepsilon) \]
考虑\(E\varepsilon = 0\),有:
\[ \operatorname{proj}(x \mid \varepsilon)=E[x]+E\left[(x-E[x]) \varepsilon^T\right]\left[E\left[\varepsilon \varepsilon^T\right]\right]^{-1} \varepsilon. \]
由于新息之间互相正交,即\(E\left[\varepsilon(i) \varepsilon^T(j)\right]=0(i \neq j)\),方差矩阵:
\[ E\left[\varepsilon \varepsilon^T\right]=\operatorname{diag}\left\{E\left[\varepsilon(1) \varepsilon^T(1)\right], \ldots, E\left[\varepsilon(k) \varepsilon^T(k)\right]\right\} . \]
因而:
\[ \operatorname{proj}(x \mid \varepsilon)=E[x]+E\left[x \varepsilon^T\right]\left(E\left[\varepsilon \varepsilon^T\right]\right)^{-1} \varepsilon=E[x]+\sum_{i=1}^k E\left[x \varepsilon^T(i)\right]\left[E\left(\varepsilon(i) \varepsilon^T(i)\right)\right]^{-1} \varepsilon(i) . \]
将求和部分拆分出\(i = 1,...,k-1\)的部分,即为\(\operatorname{proj}(\boldsymbol{x} \mid \boldsymbol{y}(1), \boldsymbol{y}(2), \cdots, \boldsymbol{y}(k-1))-E(x)\),即可证明上式。
Kalman滤波器
考虑动态系统,包括状态方程和观测方程:
\[ \begin{aligned} & \boldsymbol{X}(k+1)=\boldsymbol{\Phi} \boldsymbol{X}(k)+\boldsymbol{\Gamma} \boldsymbol{W}(k) \\ & \boldsymbol{Y}(k)=\boldsymbol{H} \boldsymbol{X}(k)+\boldsymbol{V}(k) \end{aligned} \]
称\(\Phi\)为状态转移举止,\(\Gamma\)为噪音驱动矩阵,\(H\)为观测矩阵。\(W\)为输入的白噪音,\(V\)为观测噪音。在本节中,\(W\)和\(V\)被假设为均值为0,方差分别为\(Q\)和\(R\)的不相关白噪音。
Kalman滤波器的问题是,对于观测信号\(\{Y(1), Y(2), \cdots, Y(k)\}\),求状态\(X(j)\)的线性最小方差估计值\(\hat{X}(j \mid k)\)。我们已经证明了,问题可以归结为求投影:
\[ \hat{X}(j \mid k)=\operatorname{proj}(X(j) \mid Y(1), Y(2), \cdots, Y(k)) \]
式中,\(j\)和\(k\)可以不相等,在本节中仅讨论\(j = k\),即常规意义下的kalman滤波器的情况。
根据投射定义得到递推关系:
\[ \begin{gathered} \hat{\boldsymbol{X}}(k+1 \mid k+1)=\hat{\boldsymbol{X}}(k+1 \mid k)+\boldsymbol{K}(k+1) \boldsymbol{\varepsilon}(k+1) \\ \boldsymbol{K}(k+1)=\mathrm{E}\left[\boldsymbol{X}(k+1) \boldsymbol{\varepsilon}^{\mathrm{T}}(k+1)\right]\left\{\mathrm{E} \boldsymbol{\varepsilon}(k+1) \boldsymbol{\varepsilon}^{\mathrm{T}}(k+1)\right\}^{-1} \end{gathered} \]
其中\(K(k+1)\)被称为Kalman滤波器增益。
递推Kalman滤波器建模如下:
状态一部预测:\(\hat{\boldsymbol X}(k+1 \mid k)=\Phi \hat{\boldsymbol X}(k \mid k)\)
状态更新:
\[ \begin{gathered} \hat{\boldsymbol{X}}(k+1 \mid k+1)=\hat{\boldsymbol{X}}(k+1 \mid k)+\boldsymbol{K}(k+1) \varepsilon(k+1) \\ \varepsilon(k+1)=\boldsymbol{Y}(k+1)-\boldsymbol{H} \hat{\boldsymbol{X}}(k+1 \mid k) \end{gathered} \]
滤波增益矩阵:\(\boldsymbol{K}(k+1)=\boldsymbol{P}(k+1 \mid k) \boldsymbol{H}^{\mathrm{T}}\left[\boldsymbol{H P}(k+1 \mid k) \boldsymbol{H}^{\mathrm{T}}+\boldsymbol{R}\right]^{-1}\)
一步预测协方差阵:\(\boldsymbol{P}(k+1 \mid k)=\boldsymbol{\Phi} \boldsymbol{P}(k \mid k) \boldsymbol{\Phi}^{\mathrm{T}}+\boldsymbol{\Gamma} \boldsymbol{Q} \boldsymbol{\Gamma}^{\mathrm{T}}\)
协方差阵更新:\(\begin{gathered}\boldsymbol{P}(k+1 \mid k+1)=\left[\boldsymbol{I}_n-\boldsymbol{K}(k+1) \boldsymbol{H}\right] \boldsymbol{P}(k+1 \mid k)\end{gathered}\)
\(\hat{\boldsymbol{X}}(0 \mid 0)=\boldsymbol{\mu}_0, \boldsymbol{P}(0 \mid 0)=\boldsymbol{P}_0\)
证明如下:
对状态方程两边取投影得到:
\[ \hat{X}(k+1 \mid k)=\Phi \hat{X}(k \mid k)+\Gamma \operatorname{proj}(W(t) \mid Y(1), Y(2), \cdots, Y(k)) \]
由状态方程迭代可得:
\[ X(k) \in L(W(k-1), \cdots, W(0), X(0)) \]
结合观察方程:
\[ Y(k) \in L(V(k), W(k-1), \cdots, W(0), X(0)) \]
从而得到:
\[ L(Y(1), \cdots, Y(k)) \subset L(V(k), \cdots, V(1), W(k-1), \cdots, W(0), X(0)) \]
根据假设,\(W(k)\)与集合\(\{X(0), W(0), \ldots, W(k-1), V(1), \ldots, V(k)\}\)每一个向量都保持正交关系。
根据子空间正交推论:若\(u\)和向量组\(\left\{v_1, \ldots, v_m\right\}\)均两两正交,则\(u\)与向量组线性生成空间\(span\{v_1,\ldots,v_m\}\)中的任意向量也正交。
因而:
\[ W(k) \perp L(Y(1), \ldots, Y(k)) \Rightarrow cov(W,Y) = 0. \]
根据以上推论结论,以及\(EW(k) =0\)的假设,有:
\[ \operatorname{proj}(W(k+1) \mid Y(1), Y(2), \cdots, Y(k))=0 \]
故:
\[ \hat{X}(k+1 \mid k)=\Phi \hat{X}(k \mid k) \]
同理根据观测方程,有:
\[ \hat{Y}(k+1 \mid k)=H\hat{X}(k+1 \mid k) \]
引出新息表达式:
\[ \varepsilon(k+1)=Y(k+1)-\hat{Y}(k+1 \mid k) \]
记误差和方差阵:
\[ \tilde{X}(j \mid k)=X(j)-\hat{X}(j \mid k)\\ P(j|k) = E[\tilde X(j|k)\tilde X^T(j|k)] \]
由此可以写出根据此类定义得到的新的控制方程和观察方程:
\[ \tilde X(k+1|k) = \Phi\tilde X(k|k)+\Gamma W(k)\\ \varepsilon (k+1) = H\tilde X(k+1|k)+V(k+1) \]
以及新的递推关系:
\[ \tilde X(k+1|k+1) = \tilde X(k+1|k)-K(k+1)\varepsilon(k+1) \]
将新的观察方程带入递归关系:
\[ \begin{aligned}\tilde X(k+1|k+1) &= \tilde X(k+1|k)-K(k+1)(H\tilde X(k+1|k)+V(k+1))\\& = (I_n-K(k+1)H)\tilde X(k+1|K)-K(k+1)V(k+1)\end{aligned} \]
同样根据控制方程,可以得到:
\[ \tilde X(k|k) \in L(W(k-1), \cdots, W(0), \tilde X(0|k))\in L(W(k-1), \cdots, W(0),V(k-1), \cdots, V(0), X(0)) \]
因而有\(W(k)\perp\tilde X(k|k)\),即\(E(W(k)\tilde X^T(k|k)) = 0\)。根据控制方程:
\[ \begin{aligned}P(k+1|k) &= E[\tilde X(k+1|k)\tilde X^T(k+1|k)] \\&= E[\Phi \tilde X(k|k) \tilde X^T(k|k)\Phi^T+\Gamma W(k)W^T(k)\Gamma^T] \\&= \Phi P(k|k)\Phi^T+\Gamma Q\Gamma^T\end{aligned} \]
考虑\(V(k+1)\perp\tilde X(k+1|k)\),\(E[V(k+1)\tilde X^T(k+1|k)] =0\)。根据观察方程有:
\[ \mathrm{E}\left[\varepsilon(k+1) \varepsilon^{\mathrm{T}}(k+1)\right]=H P(k+1 \mid k) H^{\mathrm{T}}+R \]
根据递推关系有:
\[ \begin{aligned} & P(k+1 \mid k+1)=\mathrm{E}\left[\varepsilon(k+1) \varepsilon^{\mathrm{T}}(k+1)\right] \\ & =\left[I_n-K(k+1) H\right] P(k+1 \mid k)\left[I_n-K(t+1) H\right]^{\mathrm{T}}+K(k+1) R H^{\mathrm{T}}(k+1)\\& = [I_n-K(k+1)H]P(k+1|k) \end{aligned} \]
接下来,求增益\(K(k+1)\)。首先计算\(\mathrm{E}\left[X(k+1) \varepsilon^{\mathrm{T}}(k+1)\right]\) 。展开后充分考虑正交关系,得:
\[ E[X(k+1)\varepsilon^T(k+1)] = P(k+1|k)H^T \]
根据\(K(k+1)=\mathrm{E}\left[X(k+1) \boldsymbol{\varepsilon}^{\mathrm{T}}(k+1)\right]\left\{\mathrm{E}[ \boldsymbol{\varepsilon}(k+1) \boldsymbol{\varepsilon}^{\mathrm{T}}(k+1)\right]\}^{-1}\),有:
\[ K(k+1) = P(k+1|k)H^T(HP(k+1|k)H^T+R)^{-1} \]
Kalman滤波器的参数设置
再假设中,\(W\)和\(V\)被假设为高斯白噪声,且方差为\(Q\)和\(R\)。实际情况下,通常需要根据数据情况和传感器测量精度来确定噪音。
系统的\(A\)、\(H\)通常要求使用建模方式去欸的那个。由于Kalman滤波要求系统为线性系统,这两项理论上来说是不变的。在这种情况下一般使用自适应滤波。
假设系统噪音为有色噪音,例如线性有色噪音:
\[ W(k) = \Pi W(k-1)+\xi(k-1) \]
可以直接对状态增广,与\(X\)一起处理。这些处理方法在之前的动态系统中都已经记录过此处不再赘述。
非线性Kalman滤波
扩展Kalman滤波器 EKF
前述,Kalman滤波器只能处理线性问题。如在动态系统笔记中所述,对于非线性系统,最常用的处理方法就是利用线性化技巧将其转化近似线性的问题。扩展Kalman滤波正式基于这种原理。其线性化方法与动态系统中所述相同,都是将非线性函数展开并忽略二次以上的项,从而在稳定点周围形成线性化模型,再应用Kalman滤波处理。
这一部分没有什么新的原理,结合上一节内容以及动态系统相关笔记处理即可。
无迹Kalman滤波 UKF
无迹Kalman滤波(UKF)使用无迹变换(UT)来处理均值和协方差的非线性传递问题。其原理是对非线性函数的概率密度分布进行近似,不依赖于雅可比矩阵,也没有将高次项忽略,因此有较高的稳定性和估计精度。
无迹变换 UT
UT变换的方法是在原分布中按规则选取一些采样点,使得这些采样点的均值和协方差等于原分布的均值和协方差。将这些点带入非线性系统,得到相应的非线性函数值点集,并通过点集求出变换后的均值和协方差。
设一个非线性变换\(y = f(x)\),已知其均值\(\bar x\)和方差\(P\),则可通过以下\(UT\)变换得到\(2n+1\)个Sigma点\(X\)和相应的权重\(\omega\)来计算\(y\)的统计特征,\(n\)是状态\(x\)的维度:
\[ \left\{\begin{array}{l}\boldsymbol{X}^{(0)}=\overline{\boldsymbol{X}}, i=0 \\\boldsymbol{X}^{(i)}=\overline{\boldsymbol{X}}+(\sqrt{(n+\lambda) \boldsymbol{P}})_i, i=1 \sim n \\\boldsymbol{X}^{(i)}=\overline{\boldsymbol{X}}-(\sqrt{(n+\lambda) \boldsymbol{P}})_i, i=n+1 \sim 2 n\end{array}\right. \]
其中\((\sqrt{\boldsymbol{P}})^{\mathrm{T}}(\sqrt{\boldsymbol{P}})=\boldsymbol{P}\),角标\((\sqrt{\boldsymbol{P}})_i\)表示矩阵方根的第\(i\)列。其中
然后计算采样点的权重,下表\(m\)和\(c\)分别为均值的权重和方差的权重:
\[ \left\{\begin{array}{l} \omega_{\mathrm{m}}^{(0)}=\frac{\lambda}{n+\lambda} \\ \omega_{\mathrm{c}}^{(0)}=\frac{\lambda}{n+\lambda}+\left(1-a^2+\beta\right) \\ \omega_{\mathrm{m}}^{(i)}=\omega_{\mathrm{c}}^{(i)}=\frac{\lambda}{2(n+\lambda)}, i=1 \sim 2 n \end{array}\right. \]
在上两个式子中,参数\(\lambda=a^2(n+\kappa)-n\)是比例缩放参数,用来降低预测误差。\(a\)用来控制采样点的分布状态。在选取时,矩阵\((n+\lambda)P\)必须是一个半正定矩阵。
点集具备以下性质:
- Sigma点集与样本的均值和方差相同
- 任何正态分布的Sigma点集都由标准正态分布的Sigma点集变换而来。
无迹Kalman滤波
假设非线性系统有下式描述:
\[ \left\{\begin{array}{l} X(k+1)=f(x(k), W(k)) \\ Z(k)=h(x(k), V(k)) \end{array}\right. \]
其余假设与线性Kalman滤波的假设相同。无迹Kalman滤波的基本算法:
根据UT变换获得Sigma点集及其对应权值:\(\boldsymbol{X}^{(i)}(k \mid k)\)
计算Sigma点集的一步预测
\[ \boldsymbol{X}^{(i)}(k+1 \mid k)=f\left[k, \boldsymbol{X}^{(i)}(k \mid k)\right] \]
根据Sigma点集的预测值加权计算状态量的一步预测和协方差矩阵:
\[ \begin{gathered}\hat{\boldsymbol{X}}(k+1 \mid k)=\sum_{i=0}^{2 n} \omega^{(i)} \boldsymbol{X}^{(i)}(k+1 \mid k) \\\boldsymbol{P}(k+1 \mid k)=\sum_{i=0}^{2 n} \omega^{(i)}\left[\hat{\boldsymbol{X}}(k+1 \mid k)-\boldsymbol{X}^{(i)}(k+1 \mid k)\right]\left[\hat{\boldsymbol{X}}(k+1 \mid k)-\boldsymbol{X}^{(i)}(k+1 \mid k)\right]^{\top}+\boldsymbol{Q}\end{gathered} \]
根据一步预测值,在使用\(UT\)变换得到新的Sigma点集:\(X^{(i)}(k+1 \mid k)\)
将预测的Sigma点集带入观测方程,得到Sigma点集的预测观测量:
\[ \boldsymbol{Z}^{(i)}(k+1 \mid k)=\boldsymbol{h}\left[\boldsymbol{X}^{(i)}(k+1 \mid k)\right] \]
- 再加权计算系统预测观测值的均值和协方差:
\[ \begin{gathered}\overline{\boldsymbol{Z}}(k+1 \mid k)=\sum_{i=0}^{2 n} \omega^{(i)} \boldsymbol{Z}^{(i)}(k+1 \mid k) \\\left.\left.\boldsymbol{P}_{z_k, z_k}=\sum_{i=0}^{2 n} \omega^{(i)}\left[\boldsymbol{Z}^{(i)}(k+1 \mid k)-\overline{\boldsymbol{Z}}^* k+1 \mid k\right)\right]\left[\boldsymbol{Z}^{(i)}(k+1 \mid k)-\overline{\boldsymbol{Z}}^* k+1 \mid k\right)\right]^{\mathrm{T}}+R \\\boldsymbol{P}_{x_k, z_k}=\sum_{i=0}^{2 n} \omega^{(i)}\left[\boldsymbol{X}^{(i)}(k+1 \mid k)-\overline{\boldsymbol{Z}}(k+1 \mid k)\right]\left[\boldsymbol{Z}^{(i)}(k+1 \mid k)-\overline{\boldsymbol{Z}}(k+1 \mid k)\right]^{\mathrm{T}}\end{gathered} \]
- 计算Kalman增益矩阵
\[ \boldsymbol{K}(k+1)=\boldsymbol{P}_{x_i z_i} \boldsymbol{P}_{z_i z_i}^{-1} \]
- 最后,计算系统状态更新和协方差更新:
\[ \begin{gathered} \hat{\boldsymbol{X}}(k+1 \mid k+1)=\hat{\boldsymbol{X}}(k+1 \mid k)+\boldsymbol{K}(k+1)[\boldsymbol{Z}(k+1)-\hat{\boldsymbol{Z}}(k+1 \mid k)] \\ \boldsymbol{P}(k+1 \mid k+1)=\boldsymbol{P}(k+1 \mid k)-\boldsymbol{K}(k+1) \boldsymbol{P}_{z_k z_k} \boldsymbol{K}^{\mathrm{T}}(k+1) \end{gathered} \]
由此可以看出,无迹Kalman滤波使用统计估计近似得到状态概率密度函数,其实质是一种统计近似,而非解。
参考
黄小平, 王岩. 卡尔曼滤波原理及应用: MATLAB仿真[M]. 北京: 电子工业出版社, 2015.




