空洞卷积,多尺度特征融合,大核卷积
空洞卷积,多尺度特征融合,大核卷积
空洞卷积和空洞空间金字塔池化(ASPP)
空洞卷积
第一项系统使用空洞卷积的工作可能是Fisher Yu在2016年的工作。作者使用这种卷积处理图像分割任务。在文献中,作者将其称为膨胀卷积dilated convolution,与本文中使用的空洞卷积atrous convolution同义。后者名称来源于法语的à trous. 相比于一般的卷积,作者强调了其能够扩大感受野的同时不损失分辨率和覆盖的能力。
在数学上,如果将一般的卷积协作:
\[ (F * k)(\mathbf{p})=\sum_{\mathbf{s}+\mathbf{t}=\mathbf{p}} F(\mathbf{s}) k(\mathbf{t}) . \]
则空洞卷积可以被写作:
\[ \left(F *_l k\right)(\mathbf{p})=\sum_{\mathbf{s}+l \mathbf{t}=\mathbf{p}} F(\mathbf{s}) k(\mathbf{t}) . \]
其中\(l\)被称作空洞率 dilation factor.
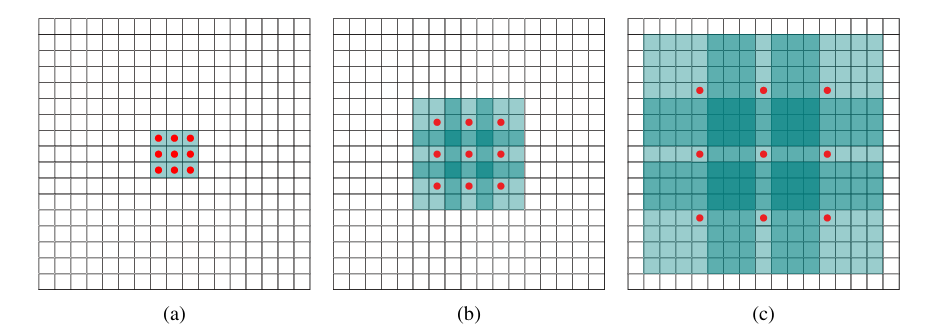
通过系统性的使用空洞卷积,可以在实现参数量线性增长的同时使得感受野指数级增长。如上图所示,首先通过一次空洞率\(1\)的空洞卷积,每个卷积的感受野为\(3\times3\);然后通过一次空洞率为\(2\)的卷积,此时每个元素的感受野上升至\(7\times 7\)。如再使用一次空洞率为\(4\)的空洞卷积,则可以得到\(15\times15\)的感受野。在这个过程中,感受野大小呈指数增长,但每次使用的卷积都使用\(3\times3\)的卷积核。
在这篇文献中,作者主要使用了串联新式的空洞卷积。通过串联不同空洞率的空洞卷积,模型可以在不降低原图片分辨率的情况下获取图片全局信息,从而实现在不增加额外参数的情况下自由控制特征响应分辨率。
空洞空间金字塔池化(ASPP)
在2017年,一篇新的研究《Rethinking Atrous Convolution for Semantic Image Segmentation》指出,除了空洞卷积已经被表述的“在不增加额外参数的情况下自由控制特征响应分辨率”的能力,使用空洞卷积还能提取多尺度特征。为此,作者提出了了一种同时使用串联和并联空洞卷积的方法。空洞空间金字塔池化并非在这项研究中首次提出,而是在这样研究中得到了优化和补足。
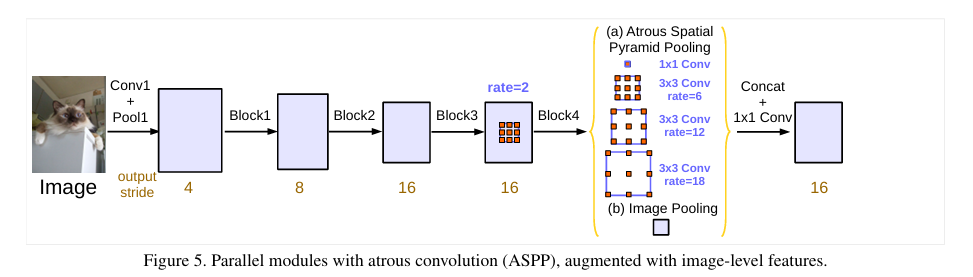
ASPP模块通常包括多个并联的不同空洞率的空洞卷积。上级神经网络会分别通过这些网络,最终再由\(1\times1\)卷积回到理想的通道数。例如,图中展示的ASPP块包括了:
- 一个\(1\times 1\)卷积分支
- 空洞率为\(6\)的一个\(3\times 3\)空洞卷积分支
- 空洞率为\(12\)的一个\(3\times 3\)空洞卷积分支
- 空洞率为\(18\)的一个\(3\times 3\)空洞卷积分支
- 图像级特征分支
前四个分支很好理解,其目的就是利用不同空洞率的空洞卷积对不同尺度特征的提取能力采集不同尺度特征。而图像级特征分支则直接对特征图做全局池化,然后再通过\(1\times1\)卷积、批量归一化映射到与其他分支相同的通道数,再使用双线性上采样至原始空间尺寸。
在每个分支都处理完成之后,将5个分支的特征图在通道维度上拼接,在通过\(1\times1\)卷积处理到所希望的通道数。
ASPP可以无缝插入各类主干网络,提供多尺度信息。
大核卷积
RepLKNet:大卷积核ConvNet架构,空洞重参数块
在小卷积核架构中增加\(3\times3\)卷积通常期望它能同时产生三种效应:
- 增大感受野;
- 提升空间模式的抽象层次,例如从角度和纹理到物体形状;
- 通过加深模型,引入更多可学习参数和非线性,从而提高模型的通用表征能力。
大卷积核具备与小核卷积不同的特性,例如其不需要通过增加深度以增加感受野。据此,作者提出大核ConvNet的四条架构设计准则:
- 使用高效结构如SE模块来增加网络深度;
- 使用膨胀重参数模块对大核卷积层进行重参数化,以在不增加推理成本的情况下提升性能;
- 根据下游任务决定卷积核大小,并通常仅在中高层使用大核;
- 在扩展模型深度时,添加3×3卷积层而非更多大核。
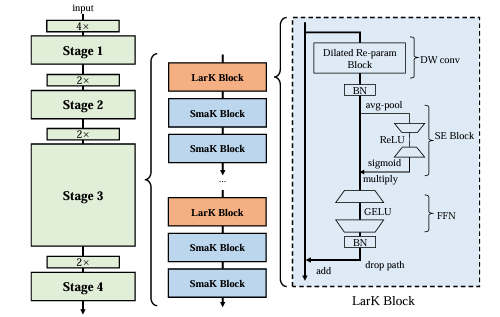
空洞重参数块 Dilated Re-param Block
大核卷积应用时,常并联小核卷积以提取更加局部的特征。再次基础上增加空洞卷积可以进一步增强捕捉稀疏模式的能力。这将增加参数量。
带小核的空洞卷积层可以等效地转换为具有稀疏大核的非空洞卷积层。若原空洞卷积卷积核大小为\(k\),通过插入\(0\)元素得到的非空洞卷积核大小为\((k-1)r+1\)。这个过程可以通过步长为\(r\),卷积核为单位核的转置卷积实现。
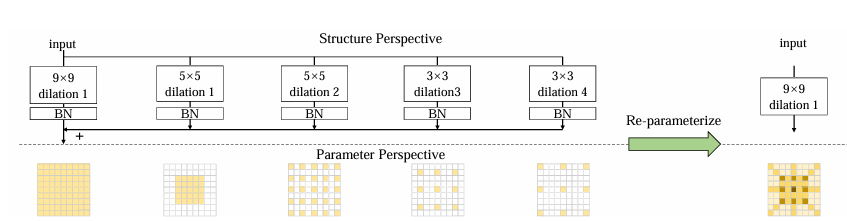
由于并联通道最终结果相加,可以在推理时将每个BN层合并到卷积层中,对空洞卷积层应用上述变换,从而将所有卷积层变换为相同大小,然后相加得到最终用于推理的大核卷积层。
PeLK:参数共享的外围卷积
外围卷积 peripheral convolution,通过共享参数将卷积复杂度从\(O(K^2)\)降低到\(O(log K)\),同时将卷积核大小提升至\(101\times101\)。
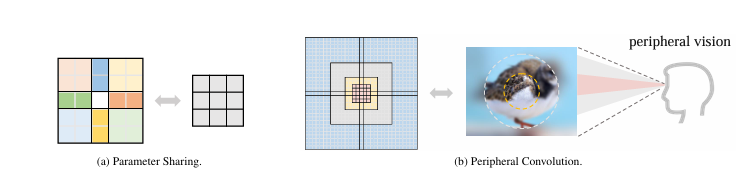
外围卷积旨在将标准二维卷积核\(w \in \mathbb{R}^{c_{\text {in }} \times c_{\text {out }} \times k \times k}\)通过空间参数共享,转化为更小的卷积核\(w_\theta \in \mathbb{R}^{c_{\mathrm{in}} \times c_{\mathrm{ont}} \times k^{\prime} \times k^{\prime}}\)。定义共享网络:
\[ S=\left[s_0, s_1, \ldots, s_{k^{\prime}-1}\right], \quad \sum_{i=0}^{k^{\prime}-1} s_i=k . \]
并根据网格划分原本的参数:
\[ Z_{a, b}=\left\{(x, y) \mid \sum_{i=0}^{a-1} s_i \leq x<\sum_{i=0}^a s_i, \sum_{j=0}^{b-1} s_j \leq y<\sum_{j=0}^b s_j\right\} \]
规定:\(w(x, y)=w_\theta(a, b)\)。从而实现小核对大核实现参数共享。对于共享网络,重新定义为:
\[ \bar{S}=\left[\bar{s}_{-r}, \bar{s}_{-r+1}, \ldots, \bar{s}_0, \ldots, \bar{s}_r\right],\bar{s}_i= \begin{cases}1, & |i| \leq r_c \\ m^{\left(|i|-r_c\right)}, & r_c<|i| \leq r\end{cases} \]
其中\(m\)为指数基数,默认取2。由此可以将卷积参数复杂度由\(O(k^2)\)降低至\(O(log k)\)。

在大卷积核中,由于一个参数覆盖极大的范围,模糊问题会比较明显。为此引入核级位置编码 Kernel-wise Positional Embedding。简单来说就是引入位置编码:
\[ h \in \mathbb{R}^{c_{\mathrm{in}} \times k \times k} \]
并采用截断正态分布初始化,作为位置编码加在卷积核上,以区分相同参数覆盖的卷积部分。
\[ Y(x, y)=\sum_{i=-r_w}^{r_w} \sum_{j=-r_w}^{r_w}(w(i, j)+h(i, j)) X(x+i, y+j) . \]
大核卷积通常有较高的通道冗余,引入部分卷积Partial Convolution。将输入通道分为两组:
\[ X_{\text {conv }}, X_{\text {id }}=\operatorname{Split}(X)=X_{:,: g}, X_{:, g:,} \quad g = 3/8 \]
仅对前者进行卷积操作,后者进行恒等变换:
\[ X_{\text {conv }}^{\prime}=\text { PeripheralConv }\left(X_{\text {conv }}\right), \quad X_{\mathrm{id}}^{\prime}=X_{\mathrm{id}} . \]
最后拼接复原:
\[ X^{\prime}=\operatorname{Concat}\left(X_{\text {conv }}^{\prime}, X_{\mathrm{id}}^{\prime}\right) . \]
PeLK 模型架构规格
- Stem: 使用
4×4卷积,步幅为4 - Stage 块数
- Tiny 模型:
[3, 3, 9, 3] - Small/Base 模型:
[3, 3, 27, 3]
- Tiny 模型:
- 默认卷积核尺寸:
[51, 49, 47, 13] - PeLK-101 卷积核尺寸:
[101, 69, 67, 13] - 中心精细区域
- 默认保留
5×5精细区 - PeLK-101 扩大至
7×7精细区
- 默认保留
- 动态稀疏: 网络宽度增益因子为
1.3×,稀疏比例40%
LSKNet:大卷积核分解和动态调整空间感受野
这项研究的目标是在要遥感目标检测中生成准确拟合目标方向的旋转边界框。作者提出广泛的上下文信息能有效地提升目标检测的准确率,而不同目标所需要的上下文信息不同。为此作者提出了LSKNet,按照作者分说法,其实现机理是:使用一组大尺度的深度可分离卷积核高效处理输入特征,并在空间上进行融合。每个卷积核的权重由输入特征动态决定,从而使得模型能够自适应选择合适的大核,并根据空间位置为每个目标调整感受野大小。
LSKNet通过重复堆叠的模块构建。每一个LSKNet模块由两个残差子模块构成:大卷积核选择子模块(LSK module),前馈网络子模块。
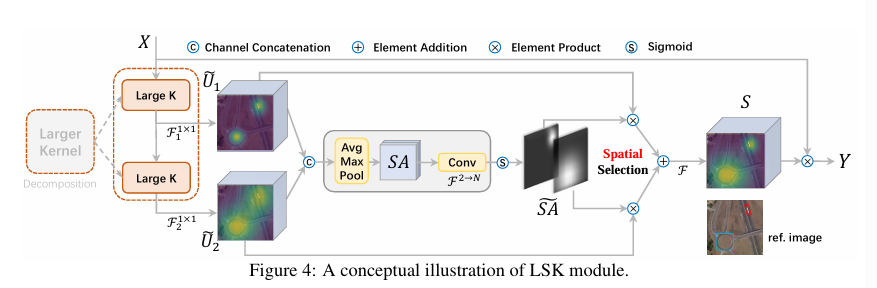
首先是大卷积核的分解部分。研究并没有直接使用大卷积核,而是将大卷积核分解为多层卷积序列,以在保证感受野的基础上减少参数量。随着深度的增加,卷积核的大小和空洞率都会增加。

如表中使用一个卷积核为5,空洞率为1的卷积和一个卷积核大小为7,空洞率为3的卷积组合,替代了原本的卷积核大小为23,空洞率为1的卷积,实现了相同的感受野。除此之外,如此方法还可以显式的产生多种不同感受野的特征。如上LSK模块结构中的\(\tilde U_1\)和\(\tilde U_2\)。
然后是卷积核选择机制,该研究使用了空间卷积核选择机制。首先,将上一步得到的不同感受野的特征拼接,分别送入通道平均池化和通道最大池化得到两个空间描述图。将两张图拼接之后,送入卷积层将通道数从2转换到N,得到N张空间注意力图,每一个对应不同的卷积核分支。然后通过sigmoid函数生成空间掩码,卷积对应卷积输出在空间位置上的权重。将权重和卷积分支输出加权,得到注意力特征。
最终将输入特征与注意力特征逐元素相乘,得到输出。
也就是说,LSK模块类似于传统的attention模块,本身的神经网络不直接处理输入,而是根据输入计算注意力向量,然后将注意力向量与输入向量相乘得到输出。
SLaK:稀疏大核卷积
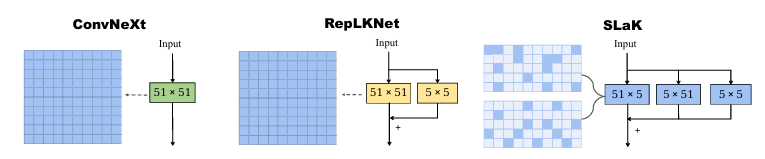
这项研究首先证明了使用常规方式突破\(31\times31\)大核极限的困难,并提出了解决方案。这种解决方案很像之前在语音分解部分提到的NMF算法。使用两个矩阵并行卷积核替代一个完整的大卷积核,即将原本的\(M\times M\)的卷积核分解为\(M\times N\)和\(N\times M\)的两个矩阵,以近似原本的大卷积核。除此之外,作者使用了之前已经提及的RepLKNet中使用的并联小核。
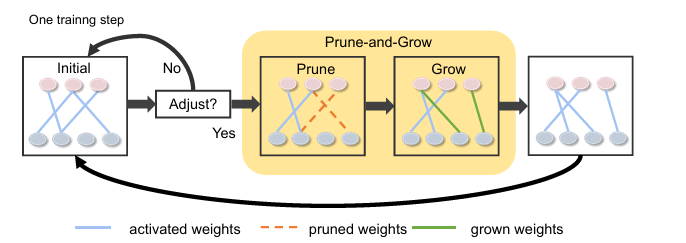
除此之外,作者在训练时引入和动态稀疏性训练,在训练中通过修建权重最小的连接并随机生长新的连接的方式,使得网络结构在训练过程中能够动态调整。关于动态稀疏性训练,可能会在之后提到。
参考文献
https://arxiv.org/abs/1511.07122
https://arxiv.org/abs/1706.05587
https://arxiv.org/abs/2203.06717
https://arxiv.org/abs/2403.07589
https://arxiv.org/abs/2303.09030
https://arxiv.org/abs/2207.03620





