电子系统课程报告
电子系统课程报告
放大器
在本节中,我们的总体目标是设计一个音频放大器。技术规格如下:
- 输入信号 \(v_e(t)\)
为音频信号,带宽在 \(20\,\mathrm{Hz}\)
到 \(20\,\mathrm{kHz}\) 之间;
- 电路输入电阻 \(R_e =
100\,\mathrm{k\Omega}\);
- 负载为阻抗 \(R_L = 4\,\Omega\)
的扬声器;
- 当输入信号为 \(100\,\mathrm{mV}\)
时,输出功率应为 \(20\,\mathrm{W}\);
- 电源为对称电源,电压为 \(V = \pm
15\,\mathrm{V}\)。
在本报告中,首先阐明将运算放大器与 B 类功率放大器结合的方案局限性,然后介绍运算放大器与 AB 类功率放大器结合的方案,后者基本满足要求。这对应原题第2和第3部分,将讨论若干方案变体。
方案2:运算放大器 + B 类功率放大器
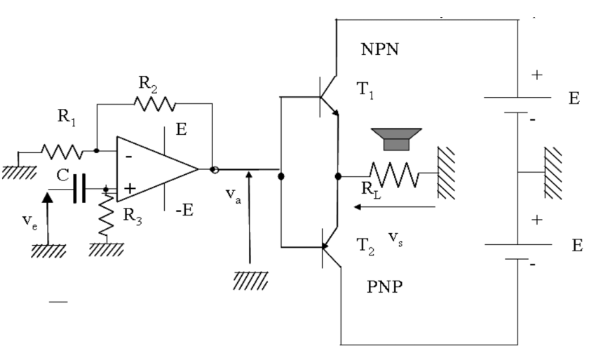
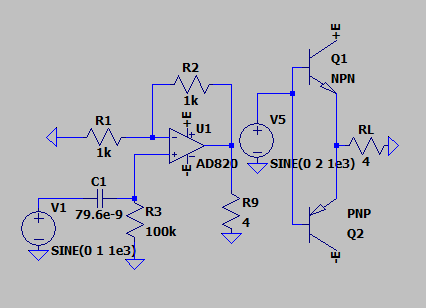
我们构建了如上电路,其中运算放大器被替换为 AD820。
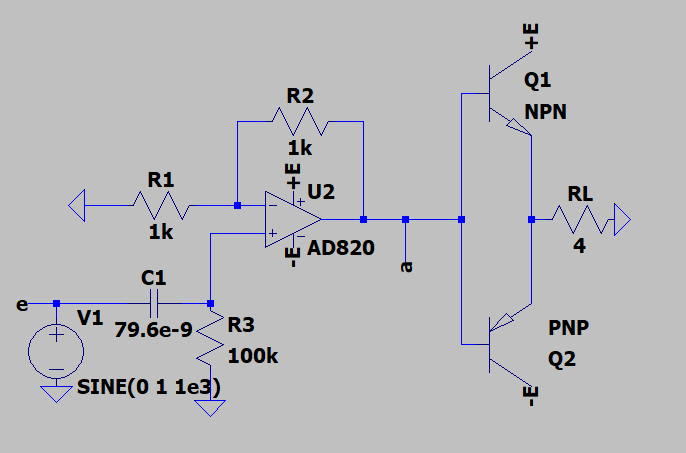
随后进行仿真,测量输入电压、运算放大器输出电压、整个电路输出电压、输入电流及两个晶体管的集电极电流,结果如下:
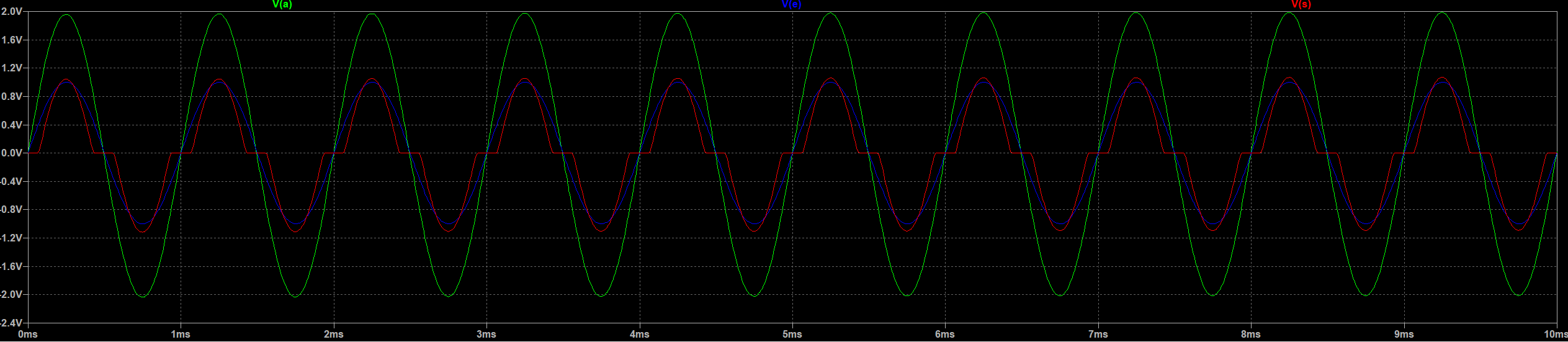
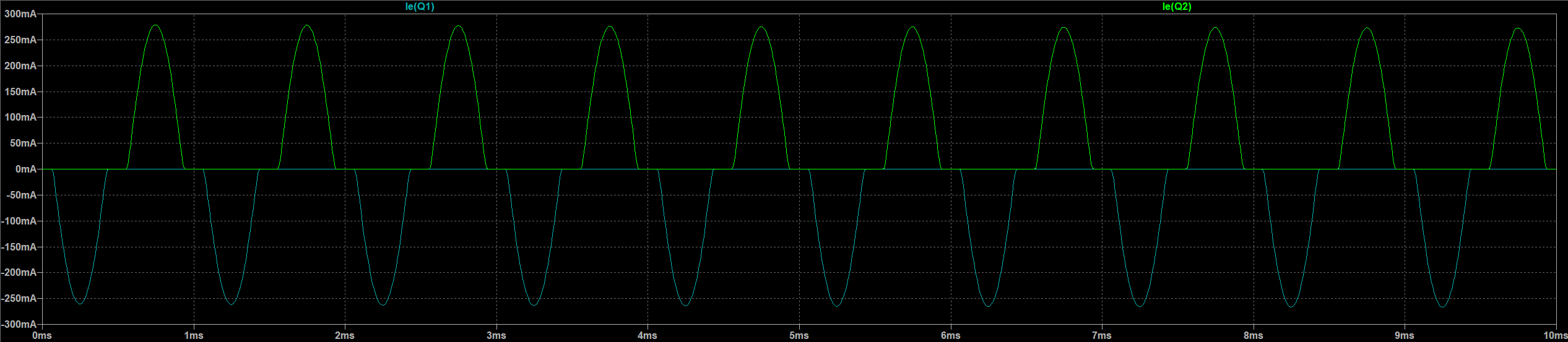
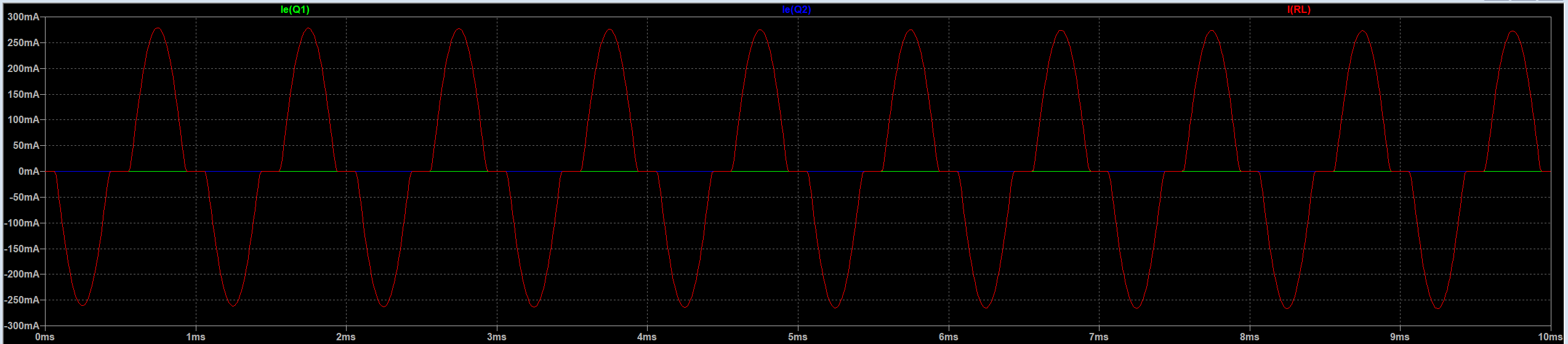
从推挽电路的集电极电流波形 \(i_{T1}\) 和 \(i_{T2}\) 可见输出电流过零点附近存在明显死区(两个晶体管均未导通)。输出电压 \(v_s\) 在过零点附近出现平坦“缺口”,表明该输出级为纯 B 类输出级,且未进行 \(V_{BE}\) 预偏置,阻碍正负半周之间连续转换,导致严重交越失真。
除了失真外,输出电压幅值与已知输入电压不符,表明系统未实现放大功能。
根据课程指导,我们尝试将信号分成两部分以验证结果:
两个放大器的输出信号如下:


可见运算放大器输出异常,验证第一个结论:运算放大器电路要求负载大于 \(750\,\Omega\)。此外,功率放大器未能实现放大功能。
方案3:运算放大器 + AB 类功率放大器
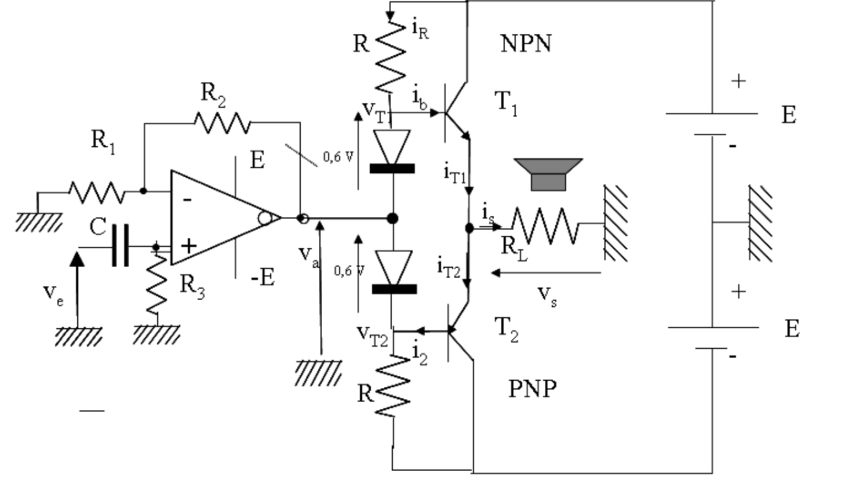
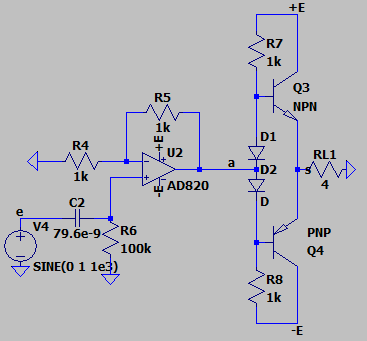
本节使用下图电路进行仿真,同样将运算放大器替换为 AD820。
仿真测量结果如下:
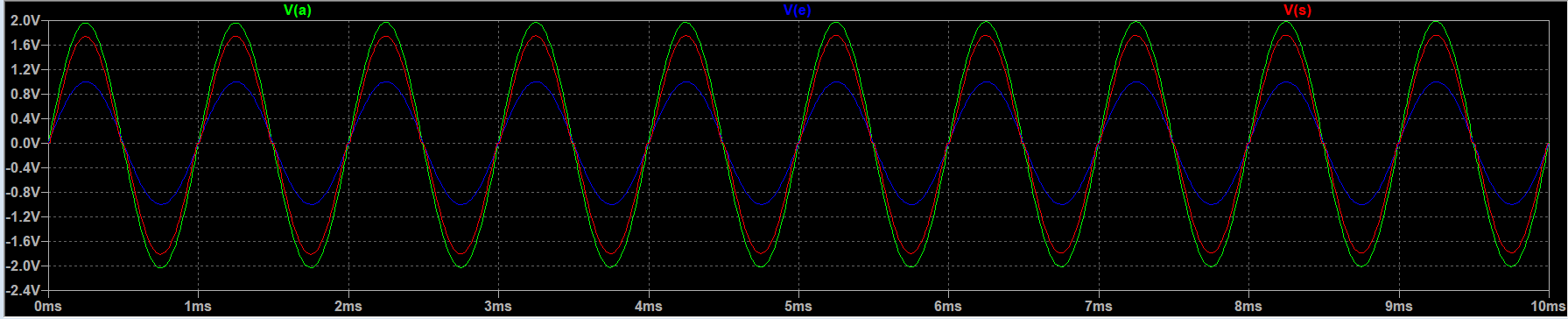
可以观察到信号已被正确放大。

还可见两个晶体管输出端信号匹配良好,输出信号几乎无失真。
以上即为 TD1 的仿真部分。
滤波器
低通滤波器
本节目标是使用 LTspice 对课程和课后练习中设计的低通滤波器性能进行数值验证。数据来自 TD 部分。
| 滤波类型 | 低通 |
|---|---|
| 截止频率 | 1 kHz |
| 停止带起始频率 | 4 kHz |
| 停止带最小衰减 | 45 dB |
| 约束 | 通带内幅度尽可能平坦 |
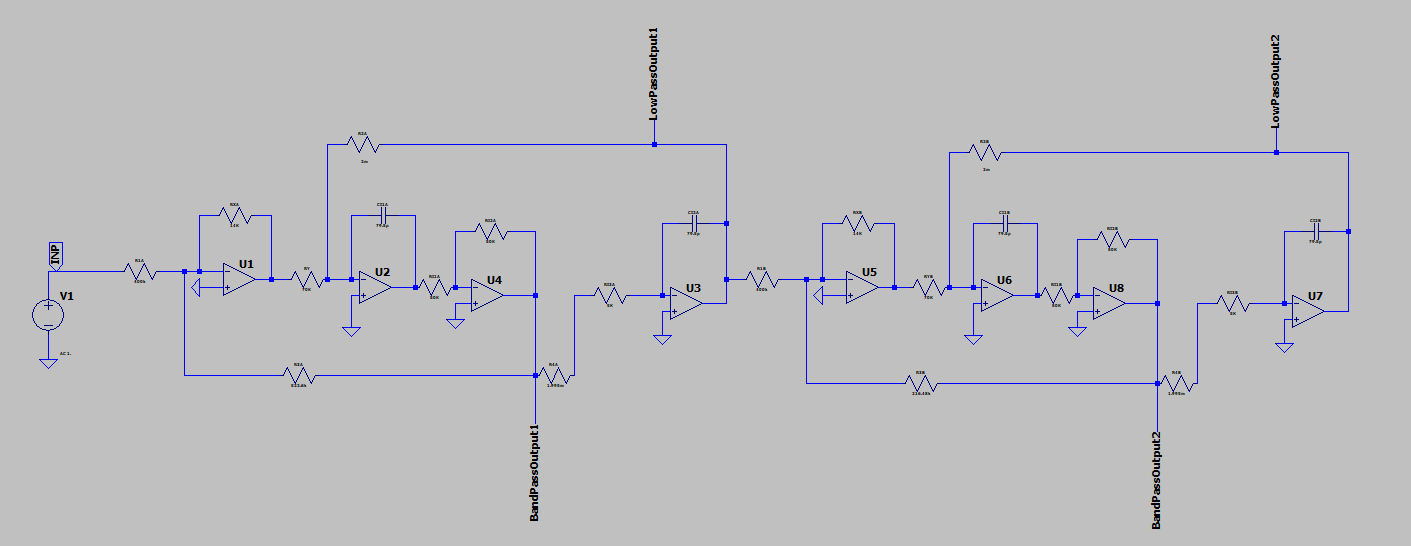
根据计算结果,我们选用四阶 Butterworth
滤波器,由两个双二阶结构(Biquad)组成。
第一结构电阻值:\(R_1 =
400\,\mathrm{k\Omega}\),\(R_2 =
2\,\mathrm{M\Omega}\),\(R_3 =
522.6\,\mathrm{k\Omega}\),\(R_4 =
1.995\,\mathrm{M\Omega}\)。
第二结构电阻值:\(R_1 =
400\,\mathrm{k\Omega}\),\(R_2 =
2\,\mathrm{M\Omega}\),\(R_3 =
216.48\,\mathrm{k\Omega}\),\(R_4 =
1.995\,\mathrm{M\Omega}\)。
我们关注第二个 Biquad 单元的输出,仿真测量结果如下:
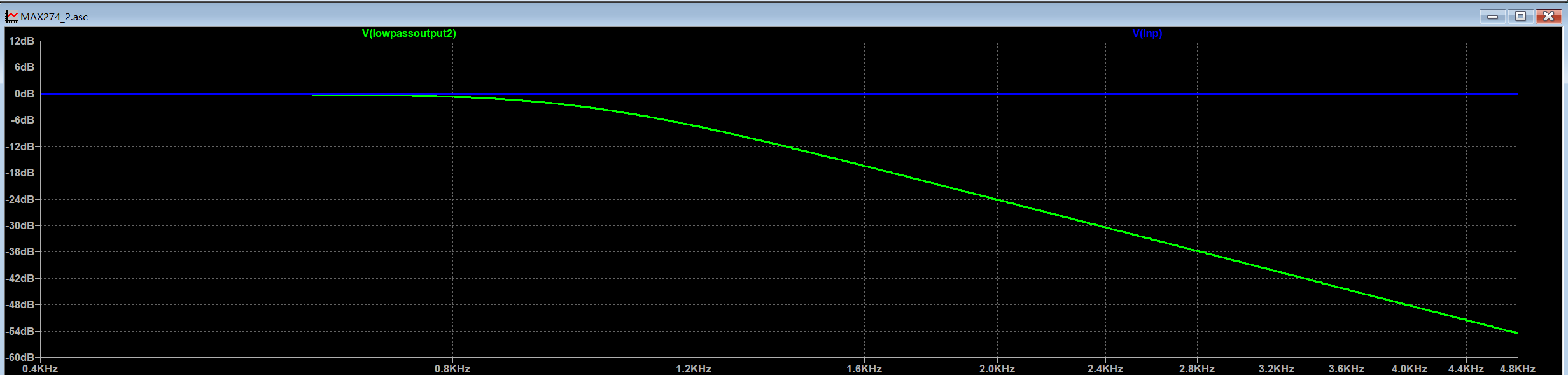
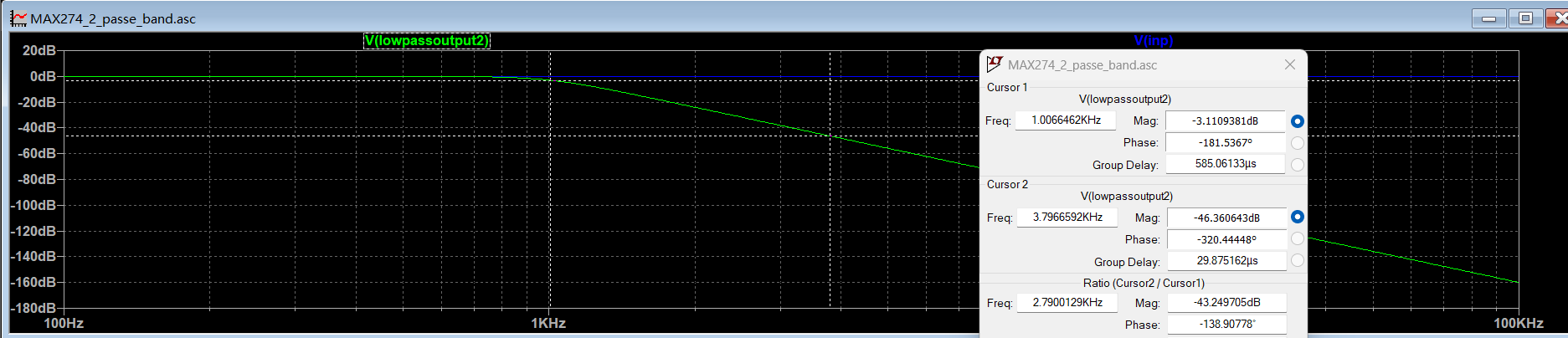
由图可见,该电路实现低通滤波:在 1 kHz 处出现 3 dB 衰减,在 4 kHz 处达到 45 dB 衰减;相位响应亦符合要求。
尽管题目要求单个 Biquad 测试,但单元仿真无法得到预期输出:
由此验证:单个 Biquad 无法实现设计功能,四阶组合结构满足规格要求。
带通滤波器
| 滤波类型 | 带通 |
|---|---|
| 中心频率 | 10 kHz |
| 通带带宽 | 1 kHz |
| 停止带带宽 | 3 kHz |
| 停止带最小衰减 | 10 dB |
| 约束 | 通带内幅度尽可能平坦 |
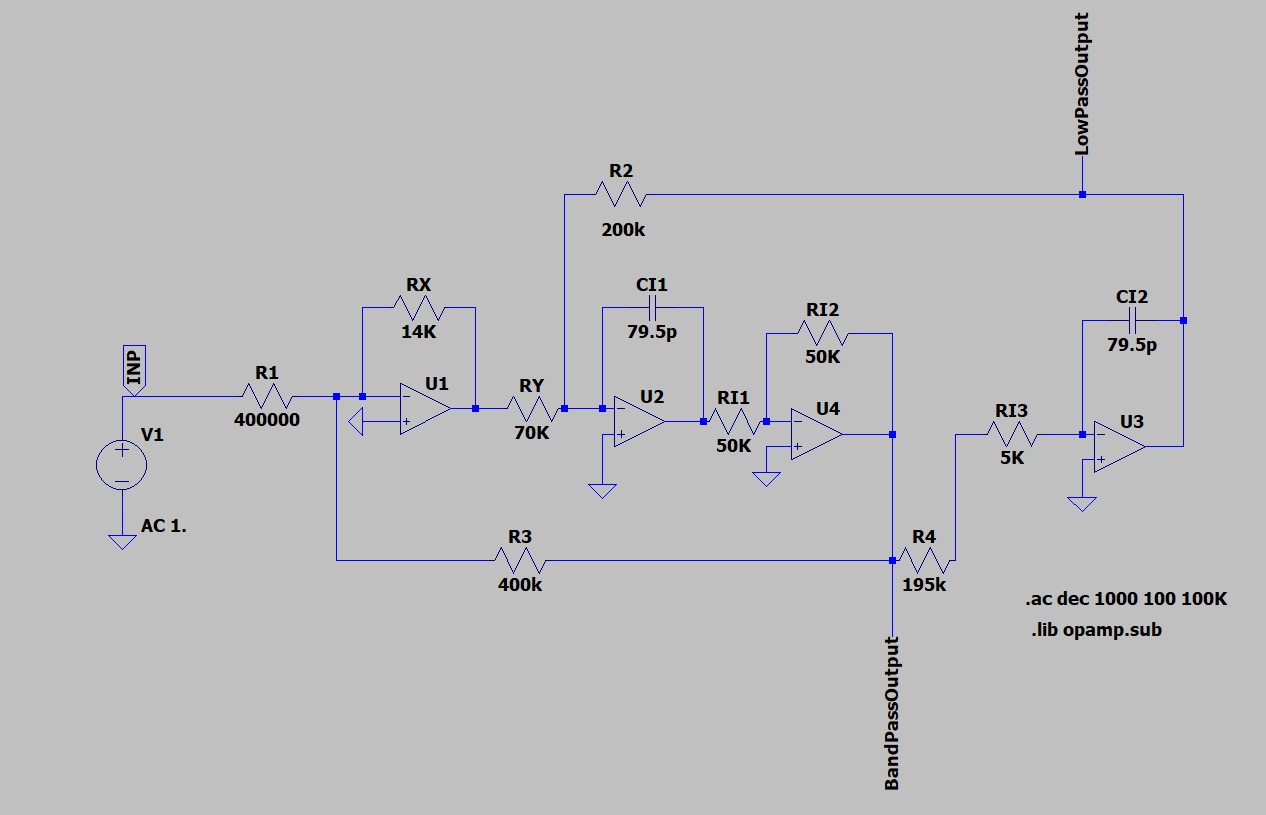
根据 TD 结果,选用二阶 Butterworth 结构,单个 Biquad,电阻值:\(R_1 = 400\,\mathrm{k\Omega}\),\(R_2 = 200\,\mathrm{k\Omega}\),\(R_3 = 400\,\mathrm{k\Omega}\),\(R_4 = 195\,\mathrm{k\Omega}\)。仿真输出如下:
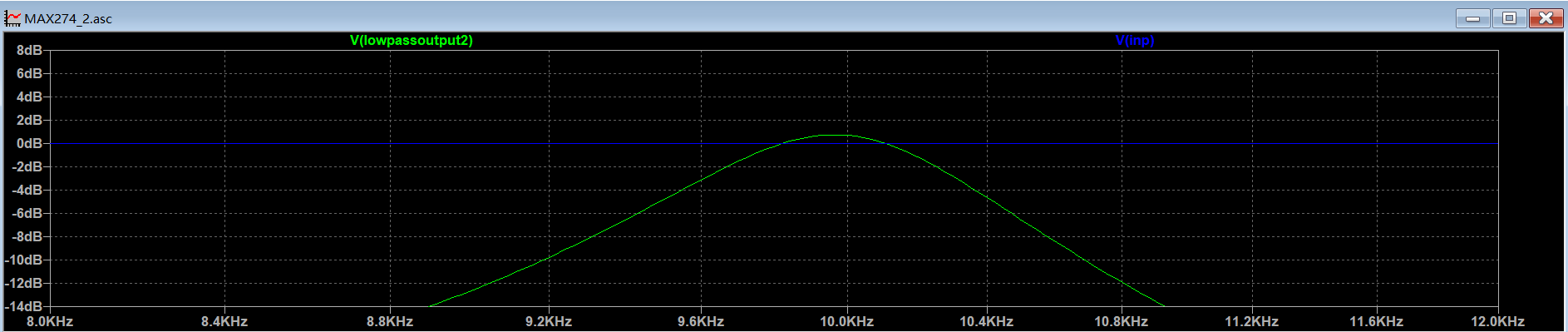

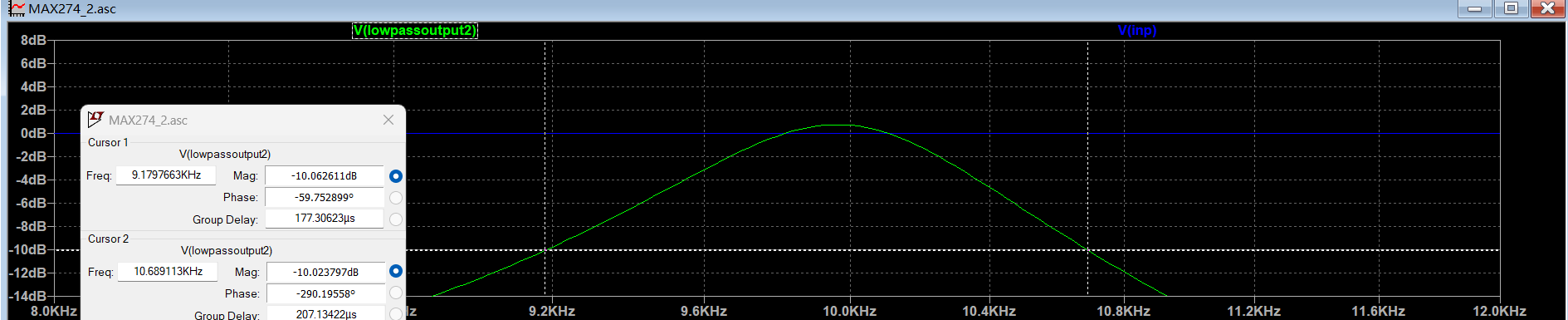
可见该电路实现带通滤波,但频率响应未完全满足规格:中心频率为 10 kHz,通带带宽小于 1 kHz;停止带在 3 kHz 处达到 ≥ 10 dB 衰减。结果与 TD 数据一致,验证了设计参数有效性。
单运算放大器带通滤波器
在 TD
中还设计了基于单运算放大器的带通滤波器,本节验证其有效性。规格同前节,参数设置如下:
\(R_1 = 2C_{1o}\), \(RC_{2o} = 2000\,\mathrm{k\Omega}\), \(C_1 = C_3 = C_{1o} = 79.2\,\mathrm{pF}\),
\(C_2 = C_{2o} = 31.8\,\mathrm{nF}\),
\(R_2 = R_3 = R =
10\,\mathrm{k\Omega}\)。

仿真输出如下:
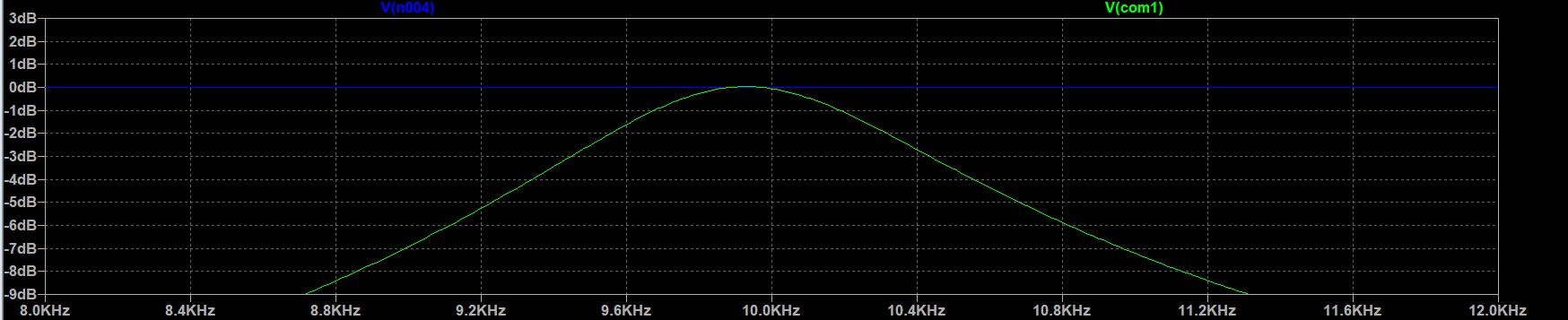
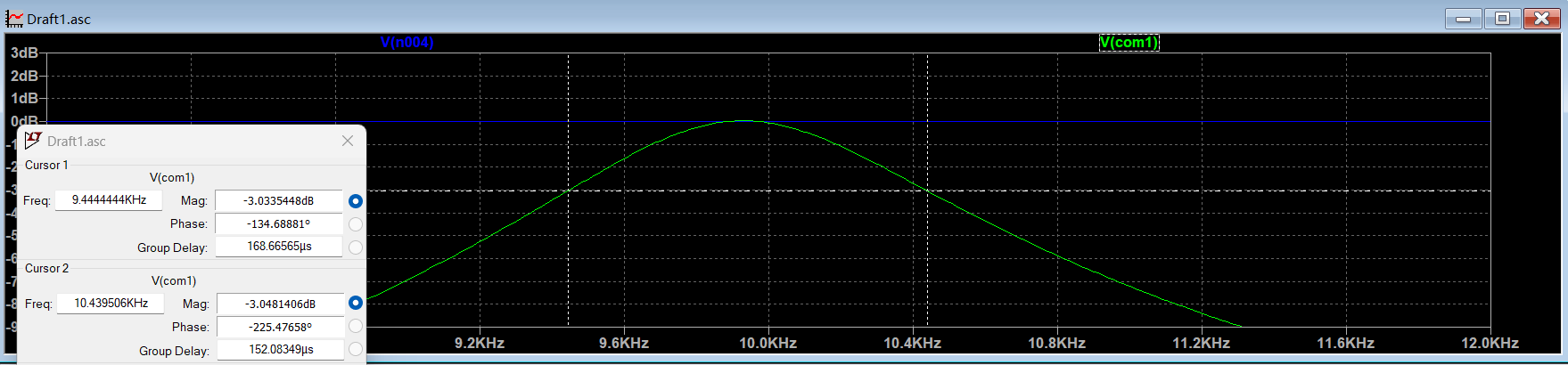
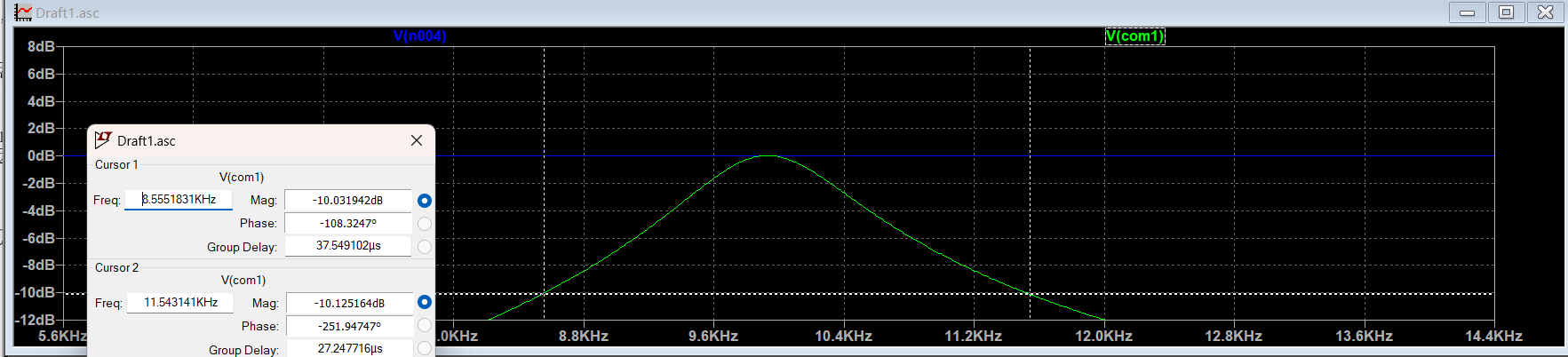
由图可见,该电路实现带通滤波:中心频率为 10 kHz,通带带宽为 1 kHz;在 3 kHz 处达到 10 dB 衰减;相位响应亦符合规格。
TP: RC 移相振荡器实验
传递函数
本节集中研究 RC 移相振荡器。我们首先进行理论计算以推导振荡器中 RC 滤波器的传递函数。随后进行电路元件参数设计与计算,以启动振荡并验证三种不同工作模式。同时讨论课堂中提及的 Wien 振荡器的若干特性。
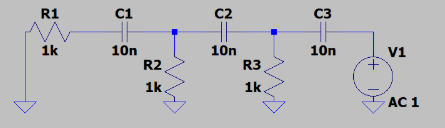
电路中共有4个节点: - 输入节点,记为 \(V_0\); - 两个中间节点,记为 \(V_1\) 和 \(V_2\); - 输出节点,记为 \(V_3\)。
定义反馈系数
\[
\beta = \frac{V_3}{V_0}.
\]
应用基尔霍夫电流定律,可得节点方程组(令 \(x = j\omega R C\)): \[ \begin{aligned} (1 + 2x)\,V_1 - x\,V_2 &= x\,V_0,\\ x\,V_1 - (1 + 2x)\,V_2 + x\,V_3 &= 0,\\ x\,V_2 - (1 + x)\,V_3 &= 0. \end{aligned} \]
解上述方程组,得到
\[
V_3 = \frac{x^3}{x^3 + 6x^2 + 5x + 1}\,V_0,
\quad
\beta(j\omega) = \frac{x^3}{x^3 + 6x^2 + 5x + 1}
= \frac{1}{1 - \frac{5}{(\omega R C)^2} - j\Bigl(\frac{6}{\omega R C} -
\frac{1}{(\omega R C)^3}\Bigr)}.
\]
接着,使用类似方法推导 Wien 振荡器的滤波传递函数。
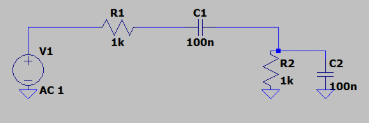
已知每段阻抗,可直接写出传递函数(令 \(x = j\omega R C\)): \[ H(s) = \frac{\frac{R}{1+x}}{R\Bigl(1 + \frac{1}{x}\Bigr) + \frac{R}{1+x}} = \frac{x}{x^2 + 3x + 1}, \] \[ \beta(j\omega) = \frac{j\omega R C}{1 - (\omega R C)^2 + j\,3\omega R C}. \]
数值研究
本节首先仿真 RC 移相振荡器滤波结构的频率响应,然后理论推导振荡频率和最小增益,并将仿真结果与理论结果对比,最后评估振荡器的稳定性。同时给出 Wien 振荡器的仿真结果。
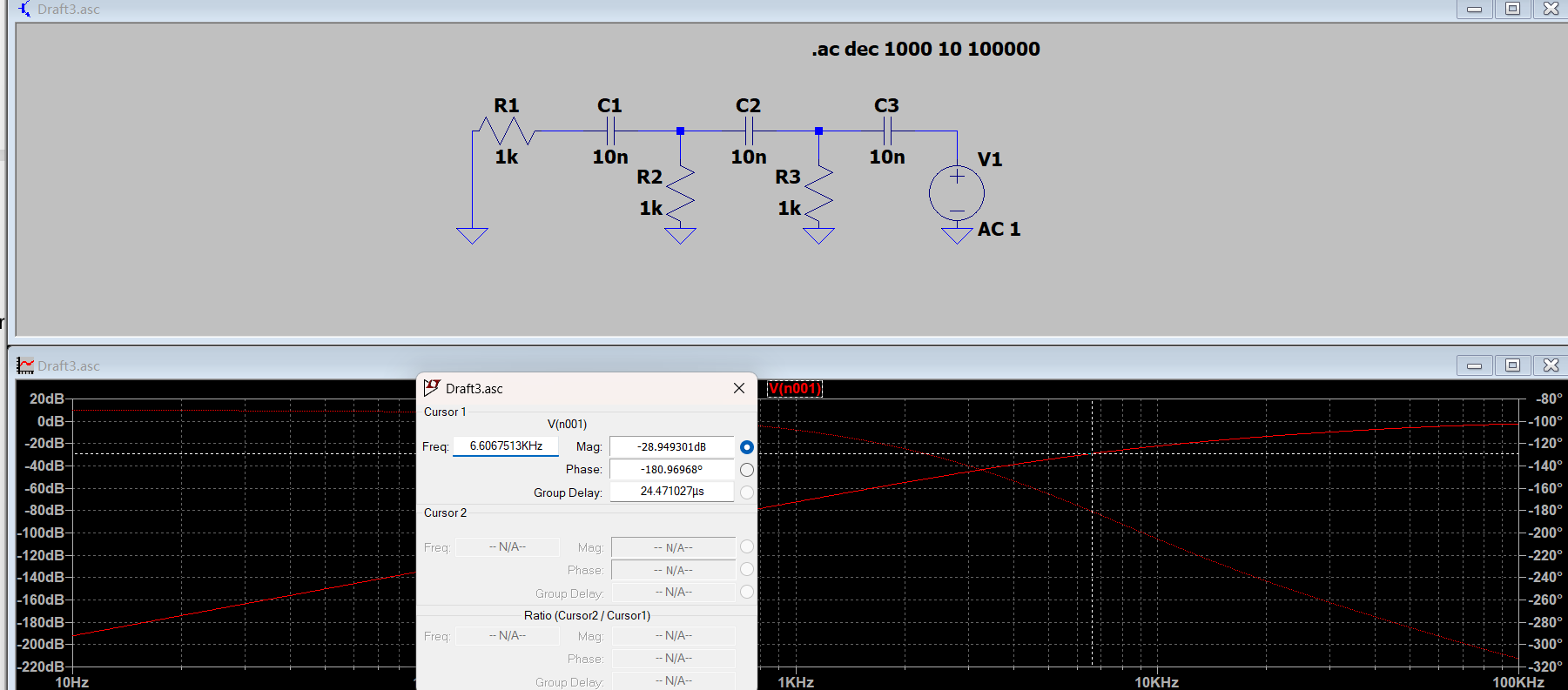
注意:当相移为 \(-\pi\) 时,幅度达到 \(-29\,\)dB(约为 \(1/29\)),对应频率约为 \(6.5\,\)kHz。
理论推导:令 \(\beta(j\omega_0)\in\mathbb{R}\),得
\[
\frac{6}{\omega_0 R C} = \frac{1}{(\omega_0 R C)^3}
\quad\Longrightarrow\quad
\omega_0 = \frac{1}{\sqrt{6 R C}},\quad
f_0 = \frac{1}{2\pi\sqrt{6 R C}} = 6.5\text{ kHz}.
\]
振荡条件 \(A\,\beta(j\omega_0)=1\),可得
\[
A = \frac{1}{|\beta(j\omega_0)|} = 29,
\]
与仿真结果一致。
取靠近 \(f_0\) 的两点:
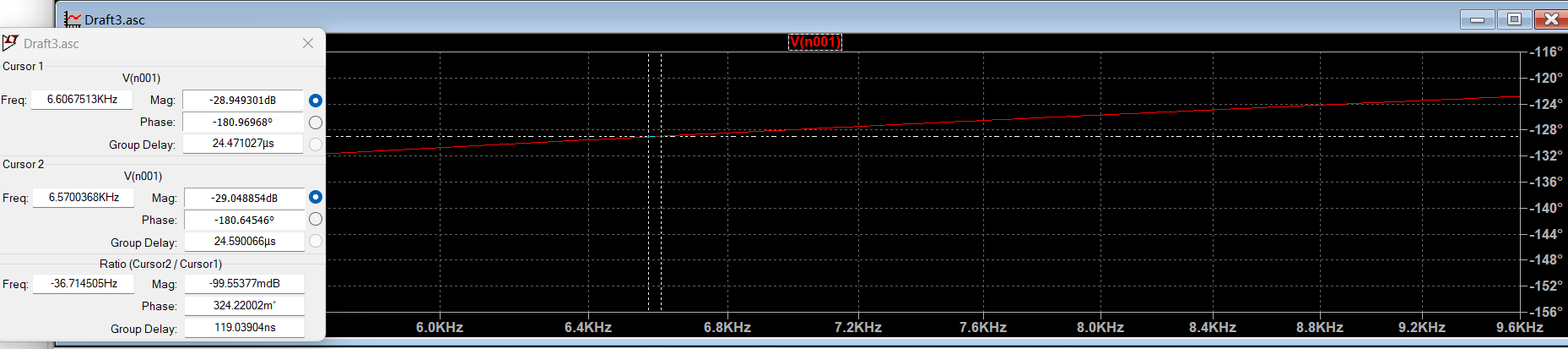
相位差
\[
\begin{aligned}
\Delta\phi &= \phi_1 - \phi_2 \\
&= -180.96968^\circ - (-180.64546^\circ) \\
&= -0.32422^\circ \approx -0.0056597\text{ rad}.
\end{aligned}
\]
频率差
\[
\begin{aligned}
\Delta f &= f_1 - f_2 = 6606.7513 - 6570.0368 = 36.7145\text{ Hz},\\
\Delta\omega &= 2\pi\,\Delta f \approx 230.74\text{ rad/s}.
\end{aligned}
\]
相位斜率
\[
\frac{d\phi}{d\omega} \approx \frac{-0.0056597}{230.74} \approx
-2.45\times10^{-5}\text{ s}.
\]
稳定性指标
\[
S(\omega_0) = \bigl|\omega_0\,\frac{d\phi}{d\omega}\bigr|
\approx 4.1398\times10^4 \times 2.45\times10^{-5} \approx 1.015.
\]

注意:当相移为 \(0\) 时,幅度达到 \(-9.5\,\)dB(约为 \(1/3\)),对应频率约为 \(1.64\,\)kHz。
理论推导:令 \(\beta(j\omega_0)\in\mathbb{R}\),得
\[
1 - \omega_0 R C = 0
\quad\Longrightarrow\quad
\omega_0 = \frac{1}{R C}.
\]
振荡条件
\[
A_0 = \frac{1}{\beta(j\omega_0)} = 3,
\]
由此得电阻比
\[
R_2 = 2\,R_1.
\]
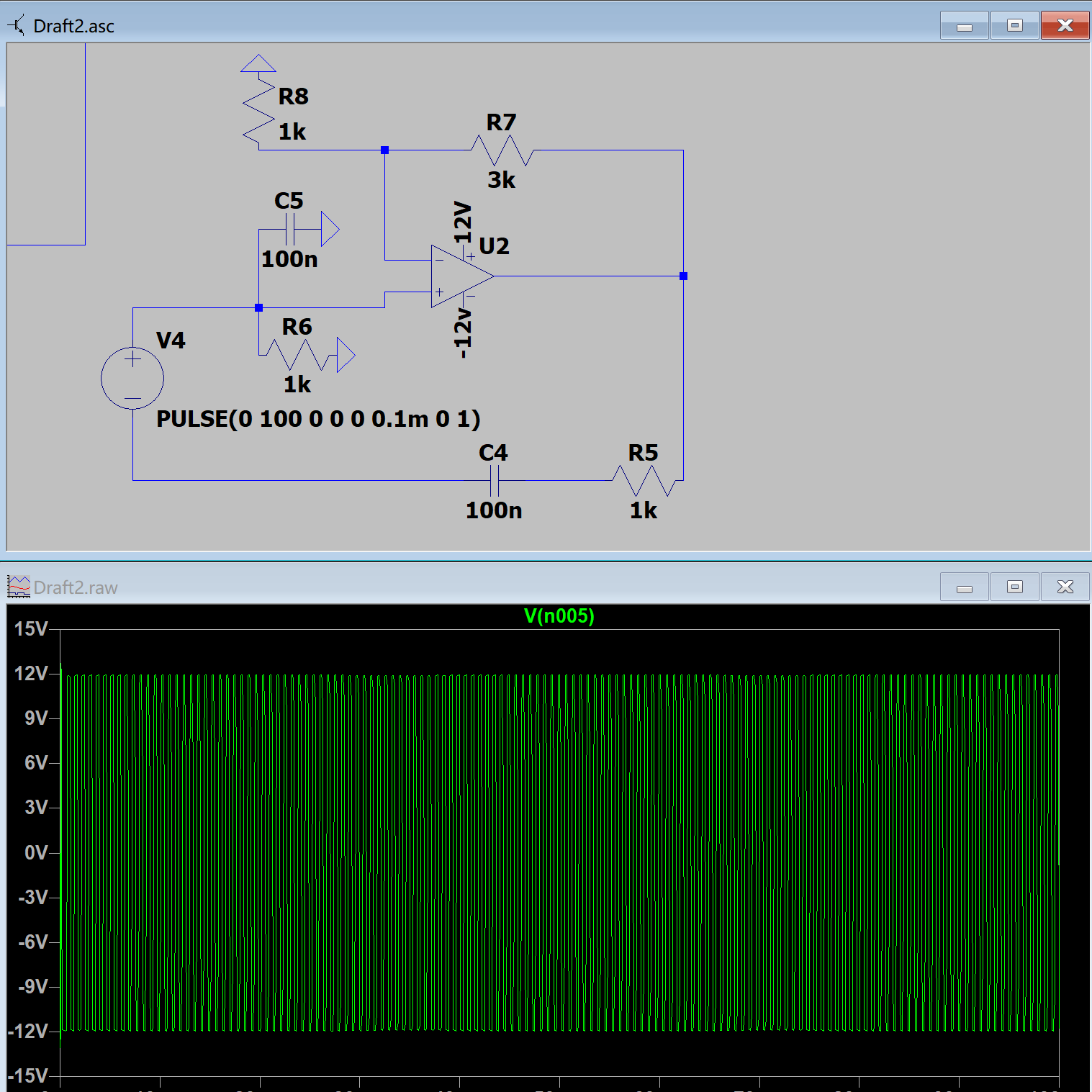
启动条件研究
在本节中,研究三种启动状态,针对 RC 移相振荡器。
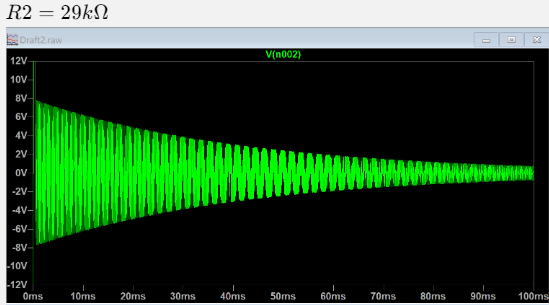

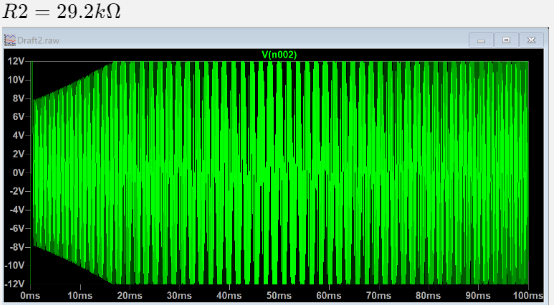
测量稳定状态下振荡频率:
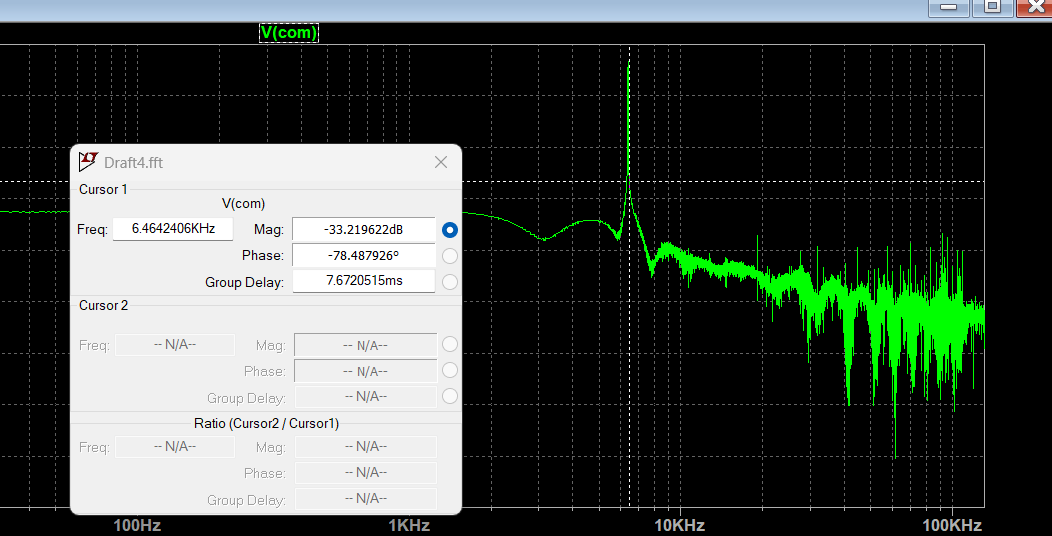
可见振荡频率与理论计算一致。
增益非线性
本节简要观察二极管引入的增益非线性。仿真电路及结果如下,可从波形图中分析非线性来源:
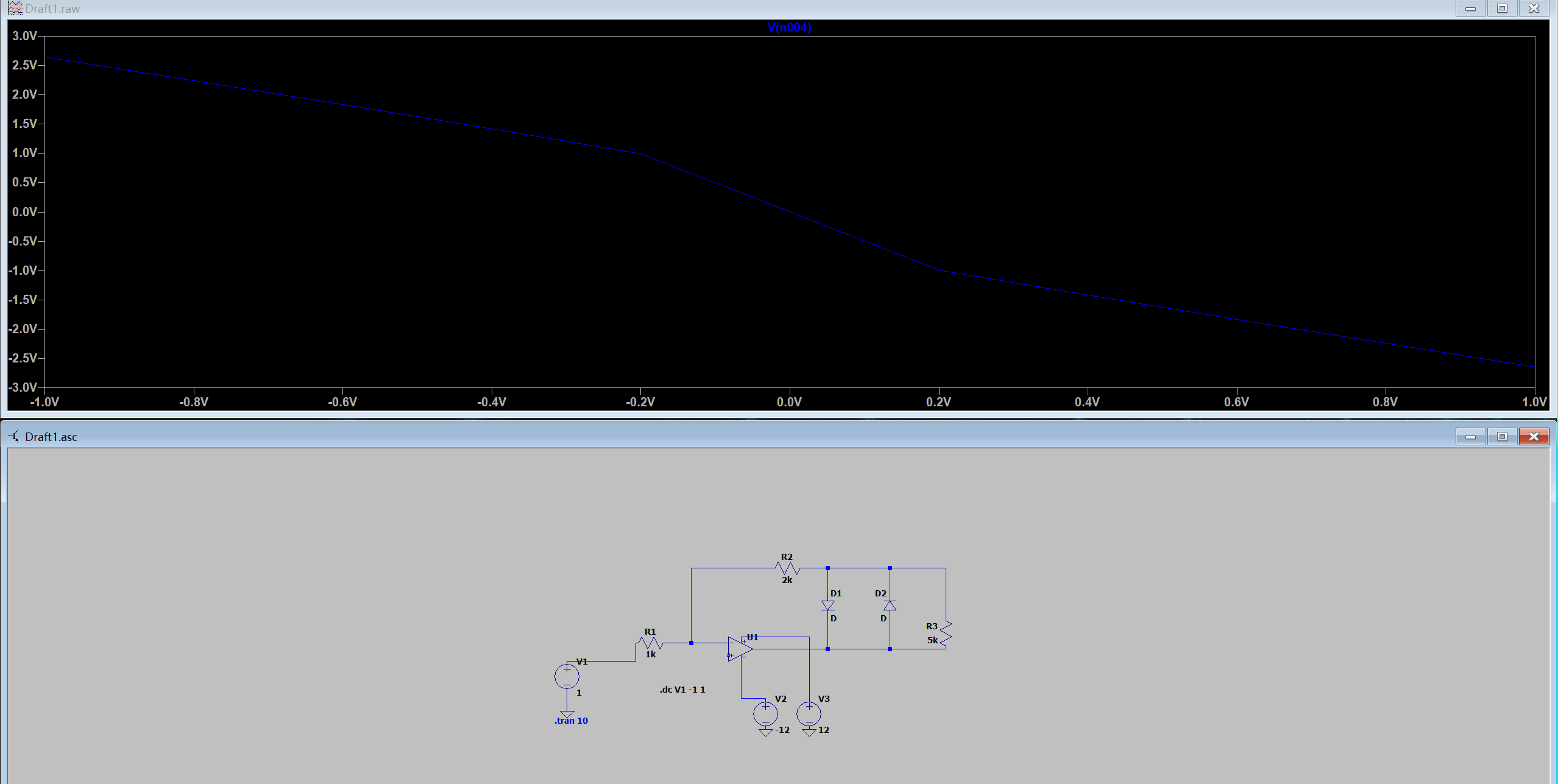
TP:CD4046B 锁相环研究
本节中,我们将利用并验证 CD4046B 锁相环的多项特性。首先确定工作频率范围;然后探讨压控振荡器与输出频率之间的关系;接着测量捕获范围和锁定范围;最后研究阶跃响应并分析动态性能。
工作频率范围
在 \(C_1 = 1\,\mathrm{nF}\)、\(R_1 = 10\,\mathrm{k\Omega}\)、\(R_2 = \infty\) 的条件下,确认 VCO 的工作频率范围。题中假设 \(V_{DD} = 10\,\mathrm{V}\)、\(V_{SS} = 0\,\mathrm{V}\),且 VCO 输入电压范围为 \([V_{SS},\,V_{DD}]\)。参照典型中心频率与电容关系图(环境温度 \(25^\circ\mathrm{C}\),\(VCO\_IN = \tfrac12 V_{DD}\),\(INH = V_{SS}\),\(R_2 = \infty\)),可得 \[ f_0 = 8\times10^4\ \mathrm{Hz}. \] 由于 \(R_2 = \infty\),处于无频偏模式,故 \[ f_{\max} = 2\,f_0 = 1.6\times10^5\ \mathrm{Hz},\quad f_{\min} = 0\ \mathrm{Hz}. \]
VCO 特性
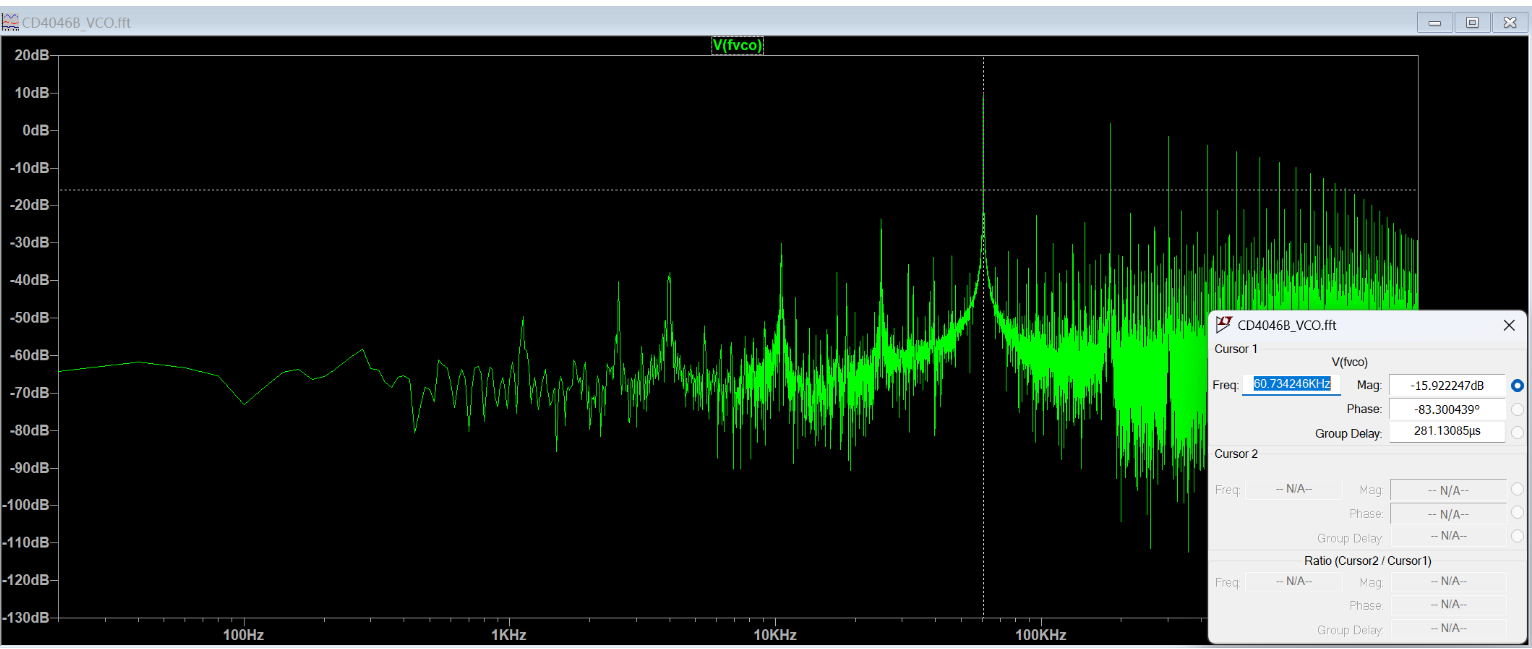
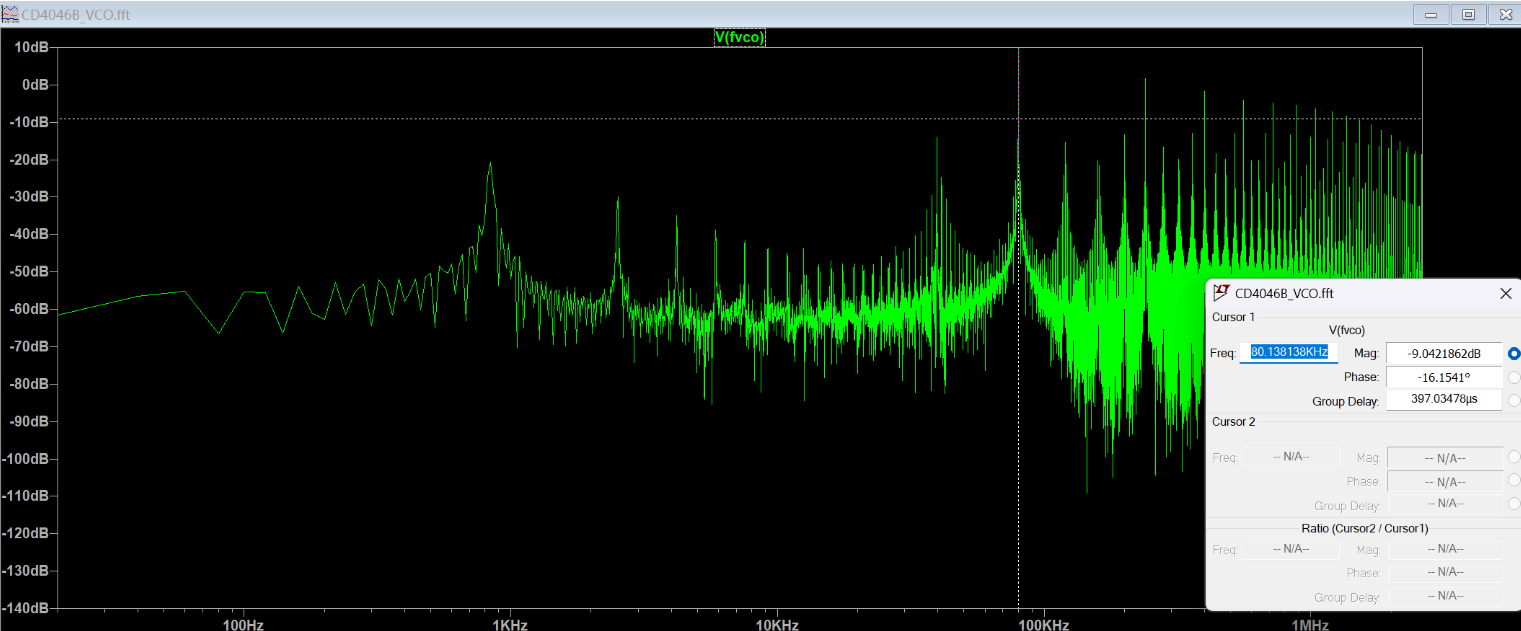
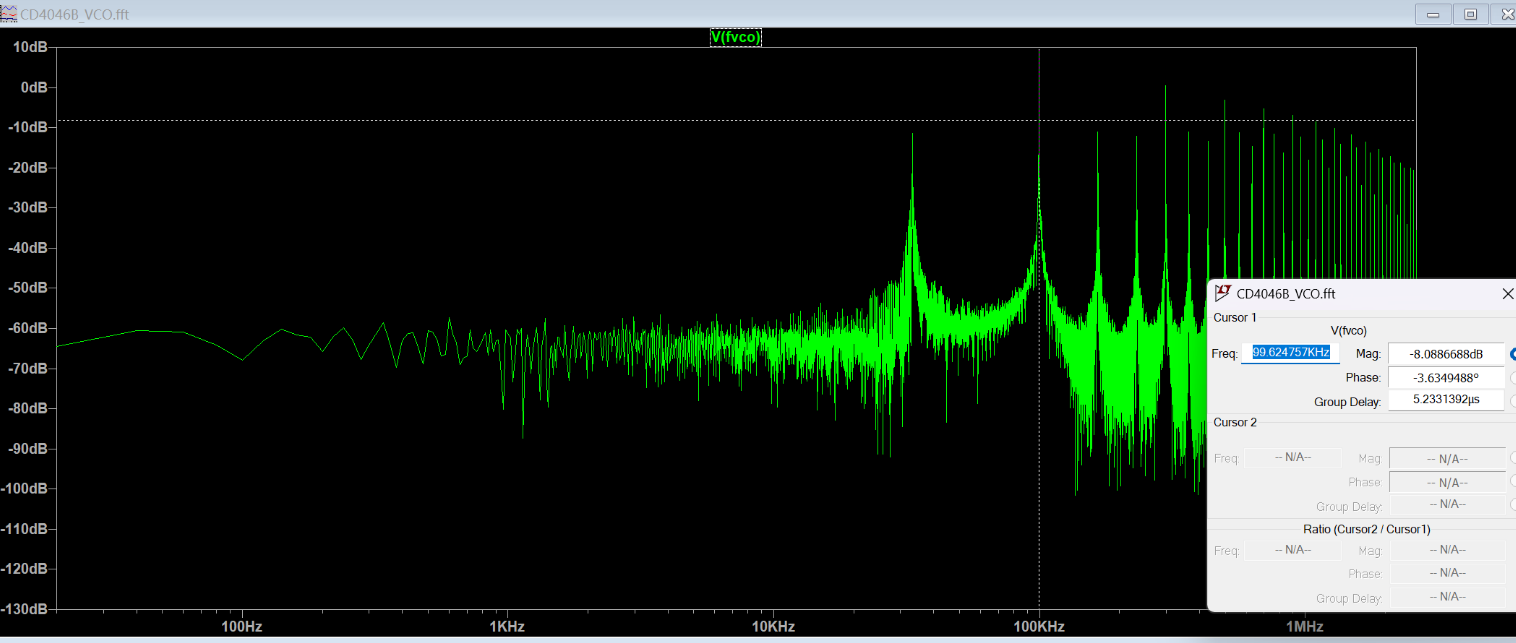
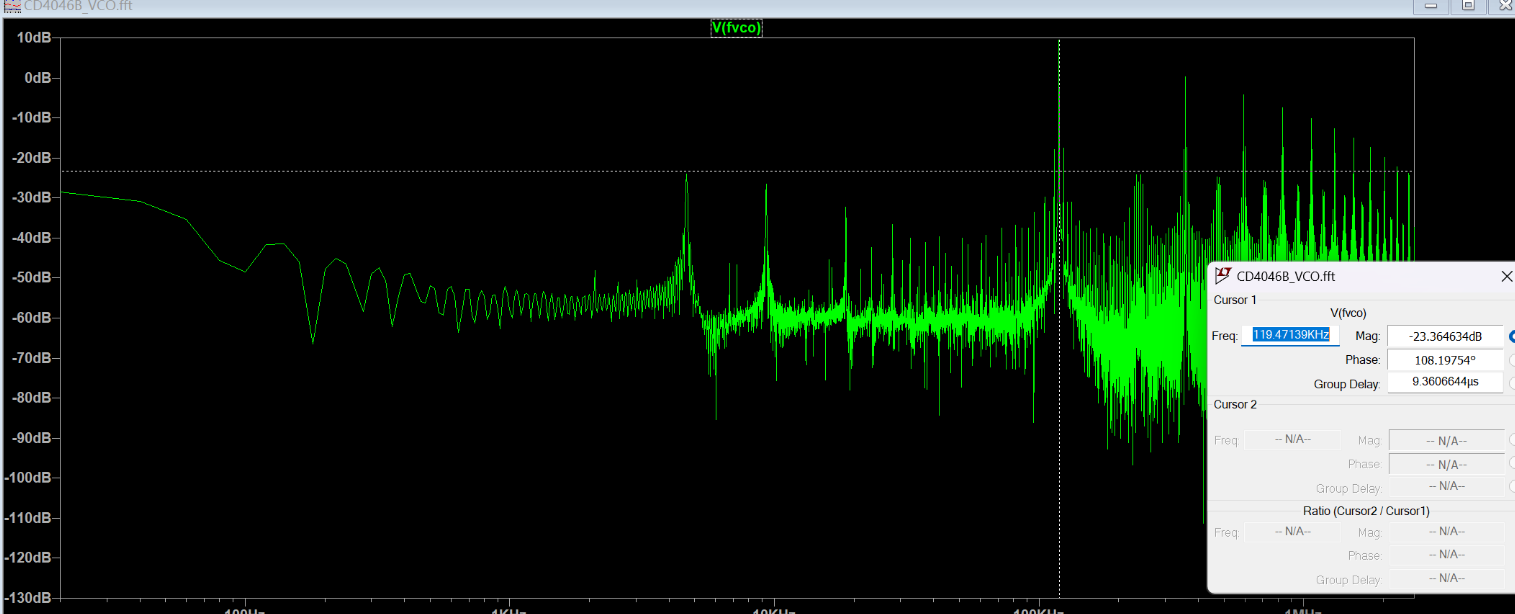
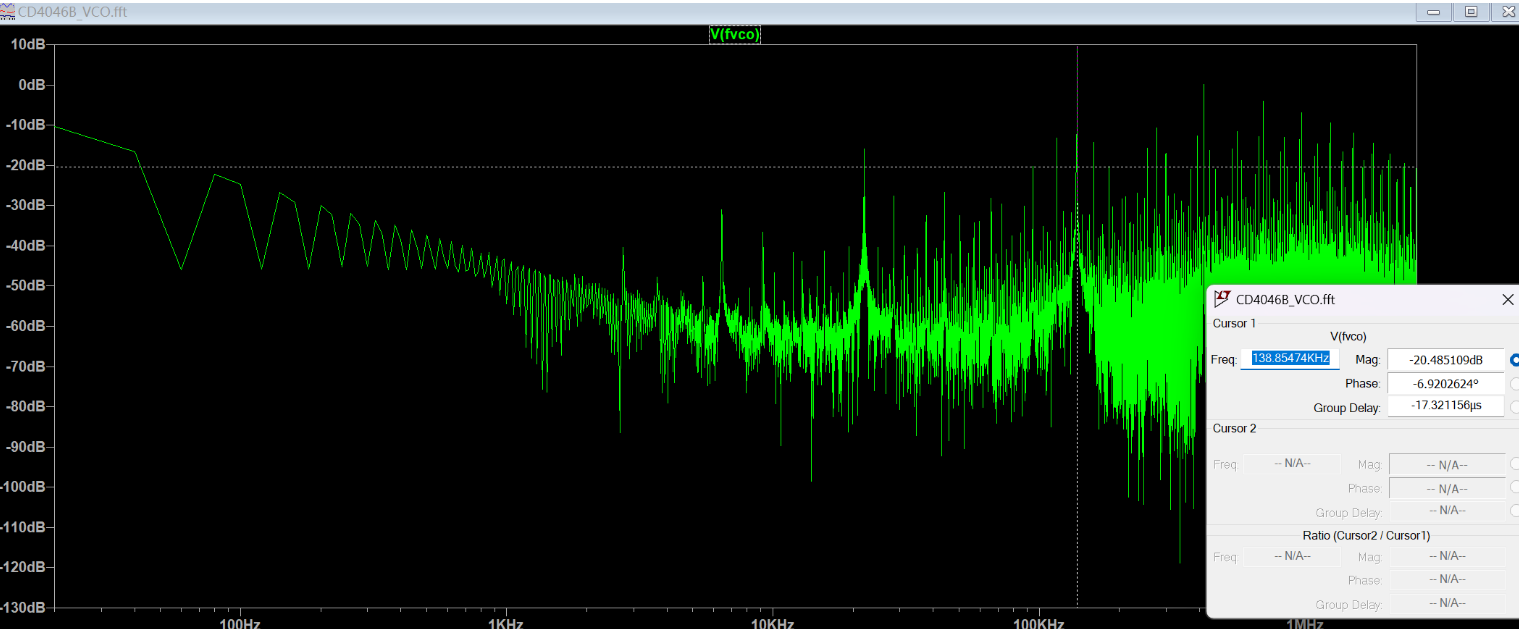
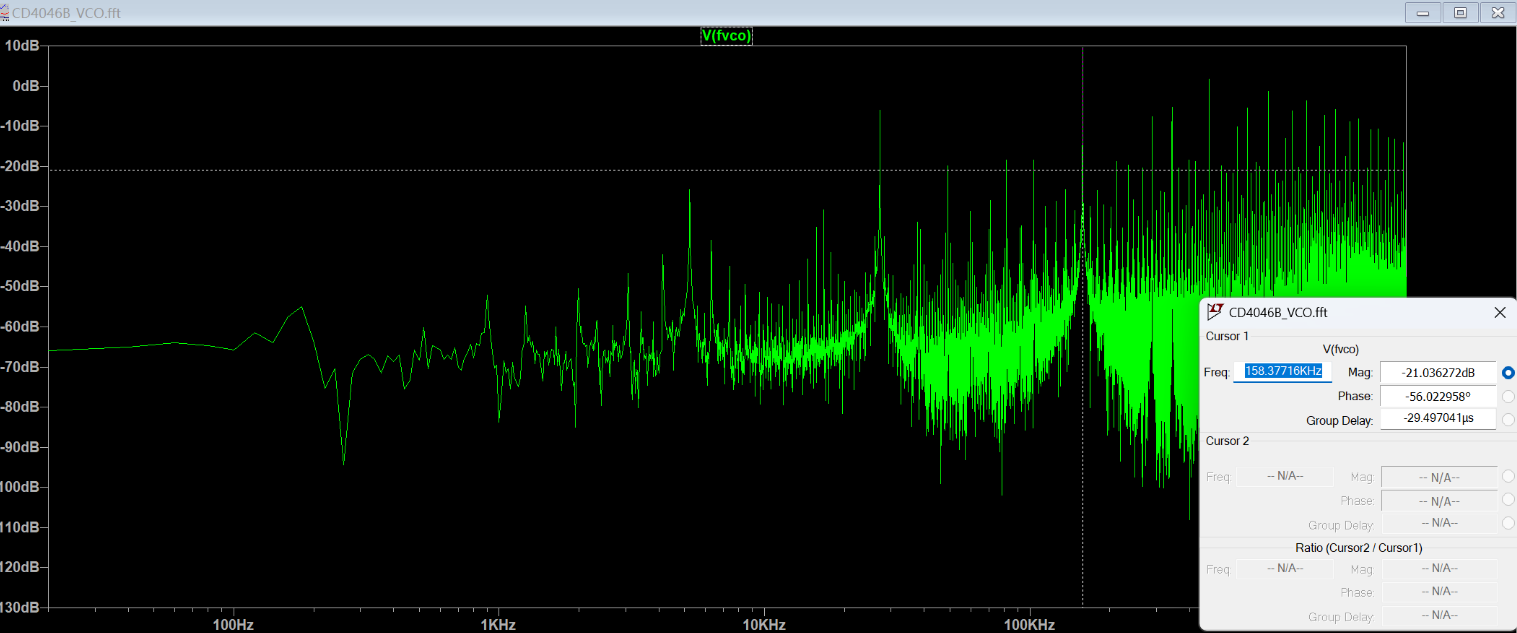
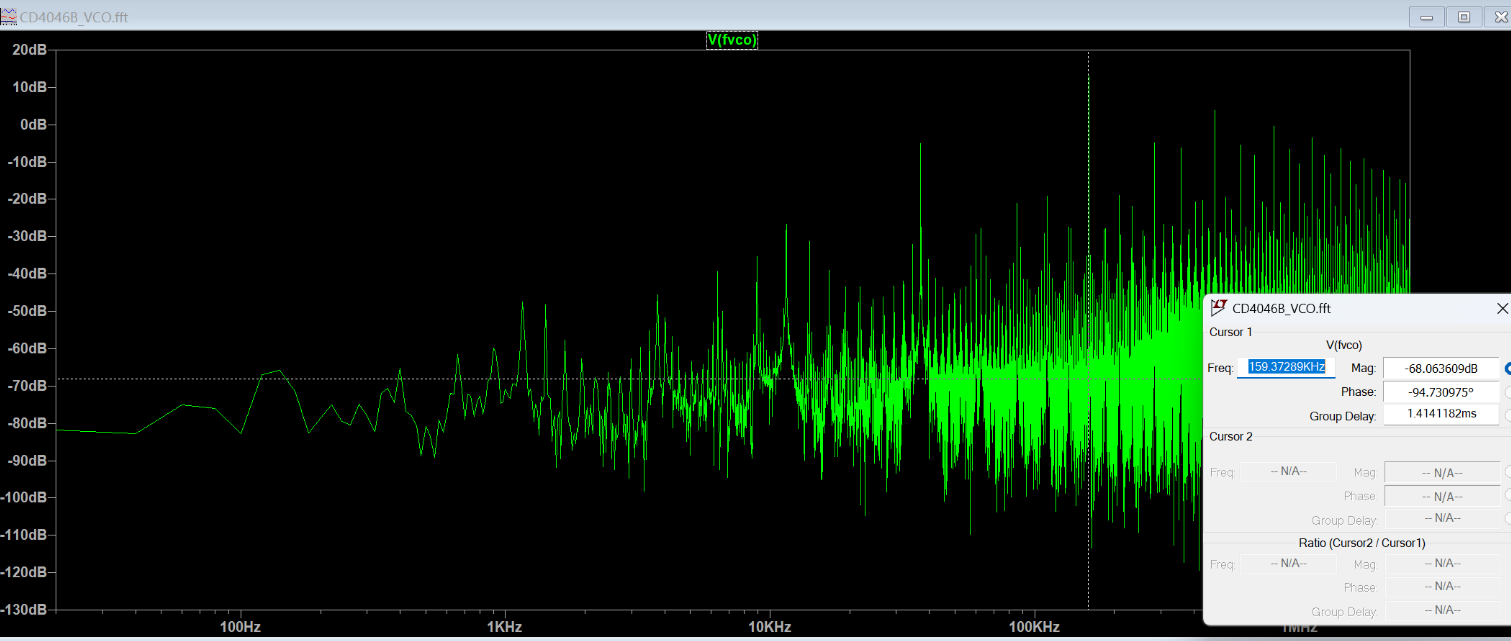
在 LTspice VCO 模型(CD4046B VCO.asc)中,设置 \(f_{\min}=1\times10^2\)、\(f_{\max}=1.6\times10^5\),并添加题中指定的电阻与电容元件。通过将输入电压
\(V_1\) 从 \(0\,\mathrm{V}\) 以 \(1\,\mathrm{V}\) 步长扫描至 \(10\,\mathrm{V}\),并使用 FFT 测量输出频率
\(f_{\mathrm{VCO}}\),导出仿真结果并绘制电压–频率关系图。结果如下:
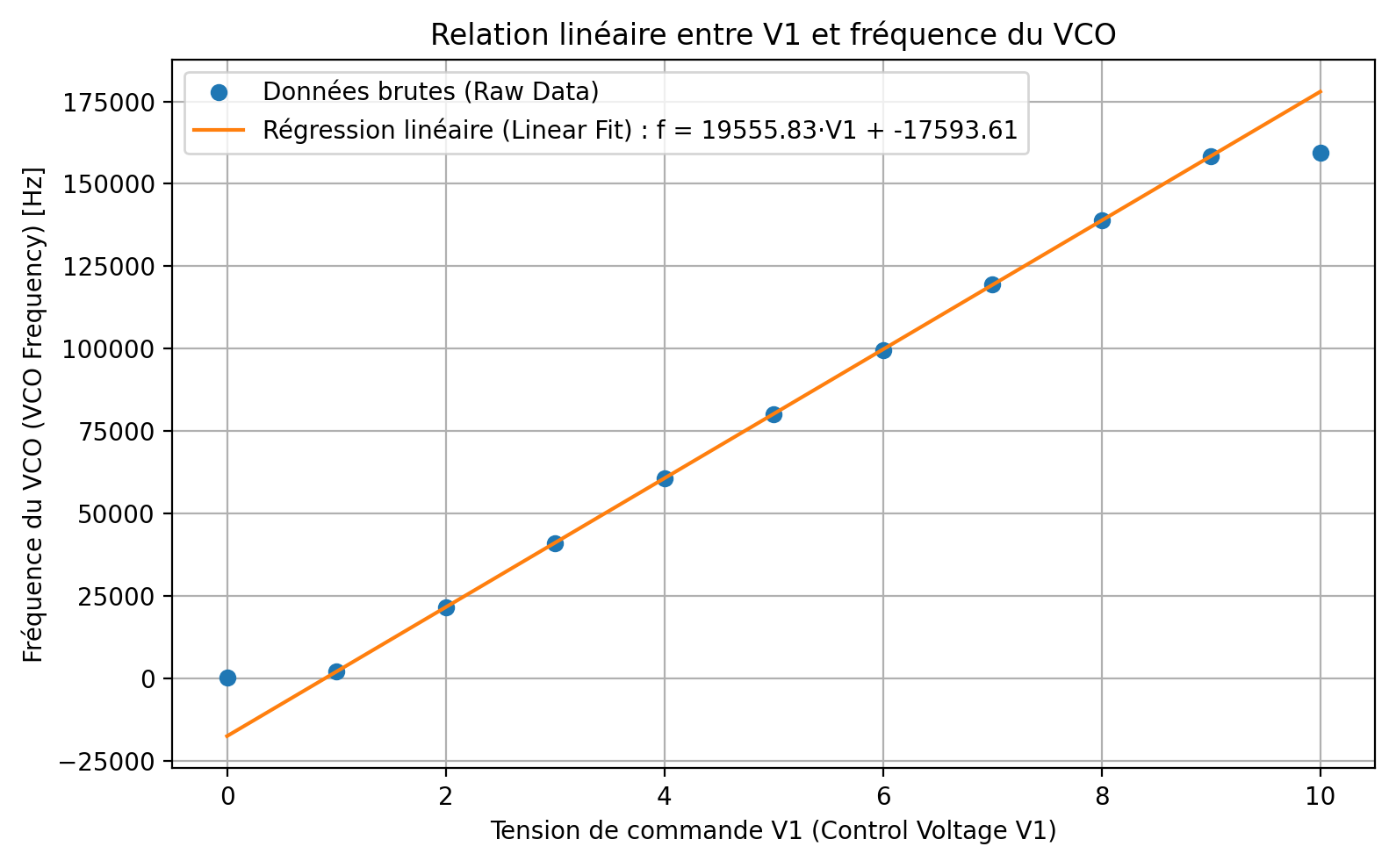
可见,当输入电压 \(V_1\) 在 \(1\,\mathrm{V}\) 至 \(9\,\mathrm{V}\) 范围内时,输出频率与输入电压呈线性关系;超出该范围后出现饱和现象。线性关系可表示为 \[ f_{\mathrm{VCO}} = 19.56\,\mathrm{kHz}\times V_{1} - 17.59. \]
捕获范围和锁定范围
使用 CD4046B sweep croissant.asc 和
CD4046B sweep décroissant.asc 进行仿真。原计划测试 \(C_2 = 10\,\mathrm{nF}\)、\(C_2 = 100\,\mathrm{nF}\)
及两种比较器,共四组;但在 \(C_2 =
10\,\mathrm{nF}\) 且使用 PC2
时仿真失败,最终仅得六组数据;后续使用信号发生器和 PC1
补充两组,总计八组数据。导出 .txt 后使用 Python
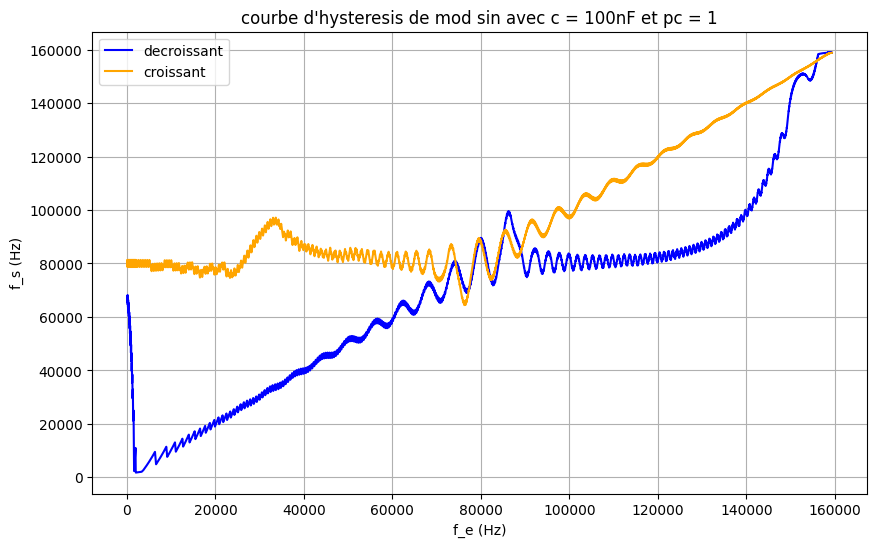
重绘,结果见附录。此处给出 \(C_2 =
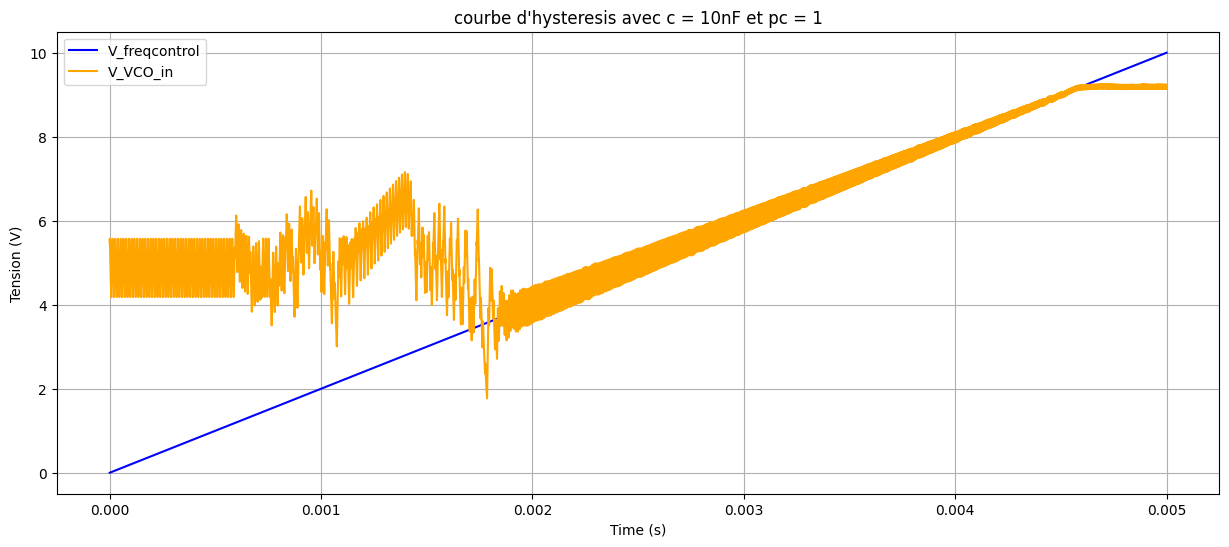
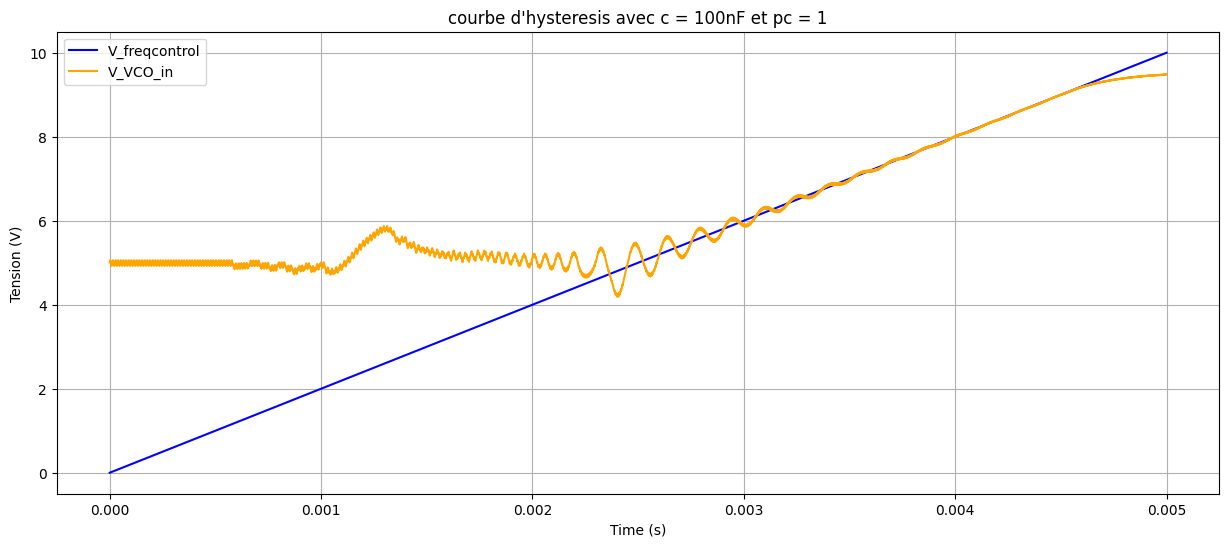
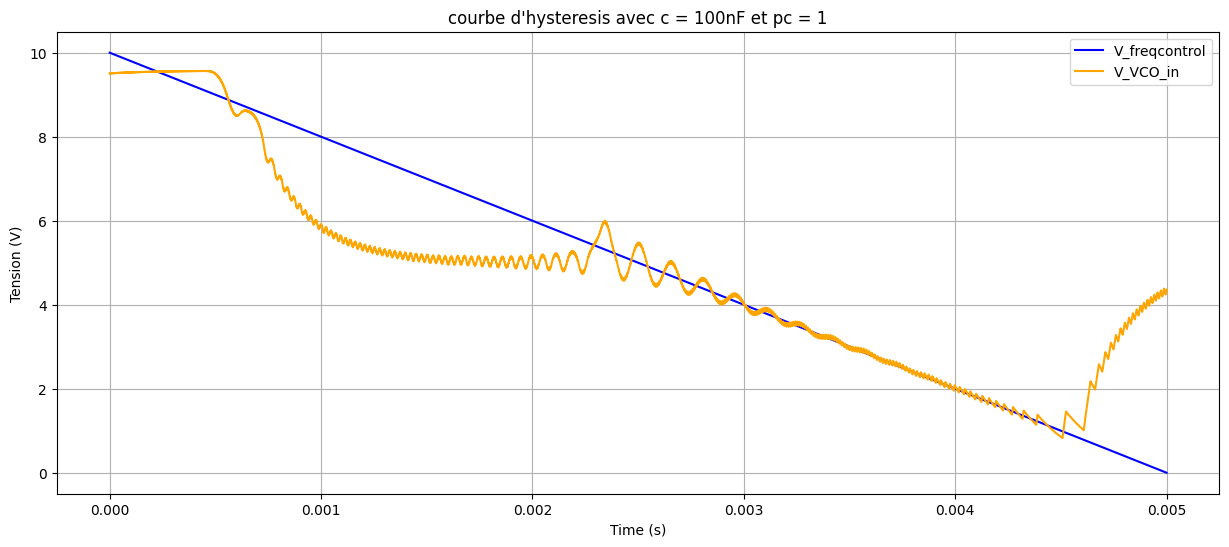
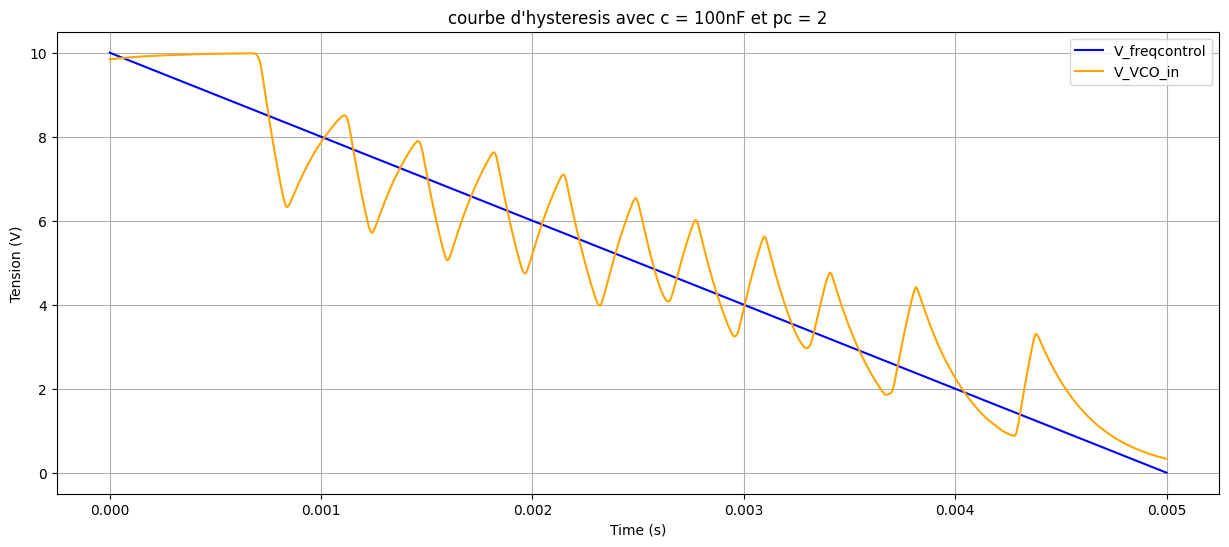
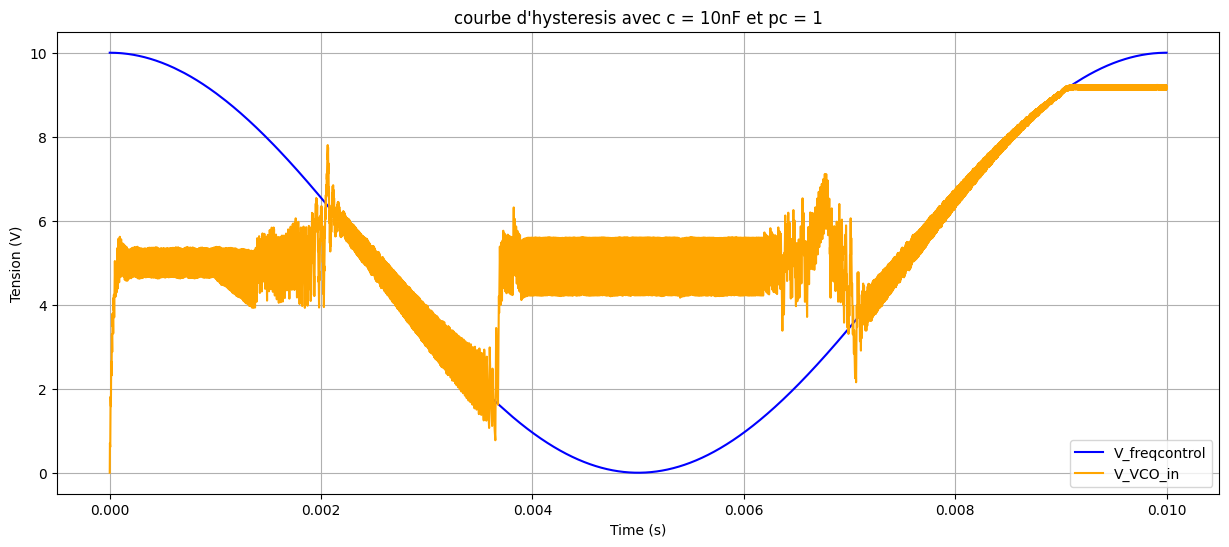
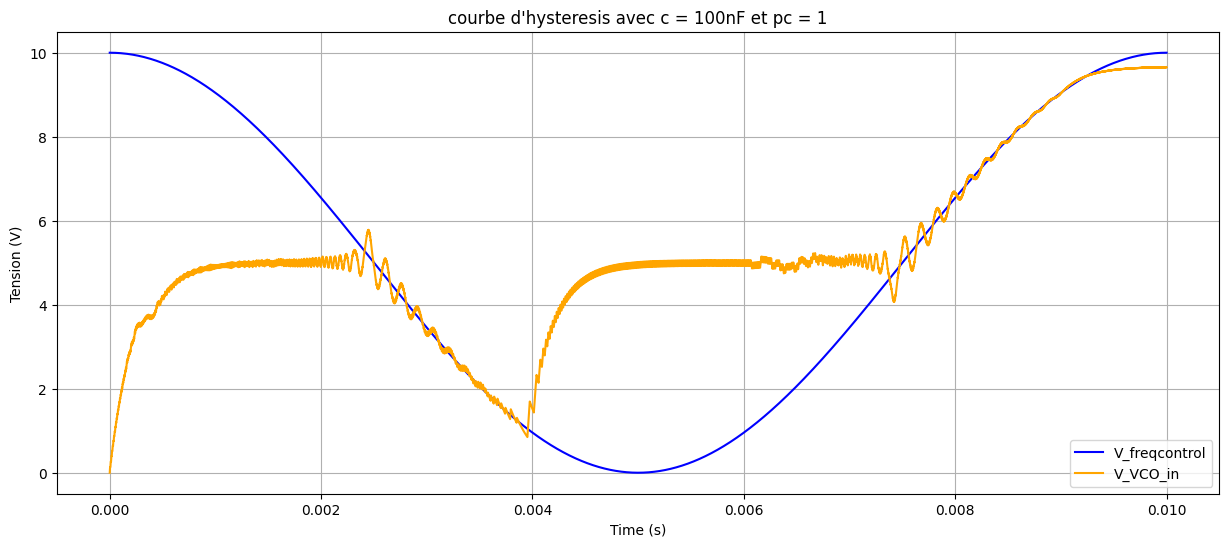
100\,\mathrm{nF}\) 时的捕获与锁定范围仿真:
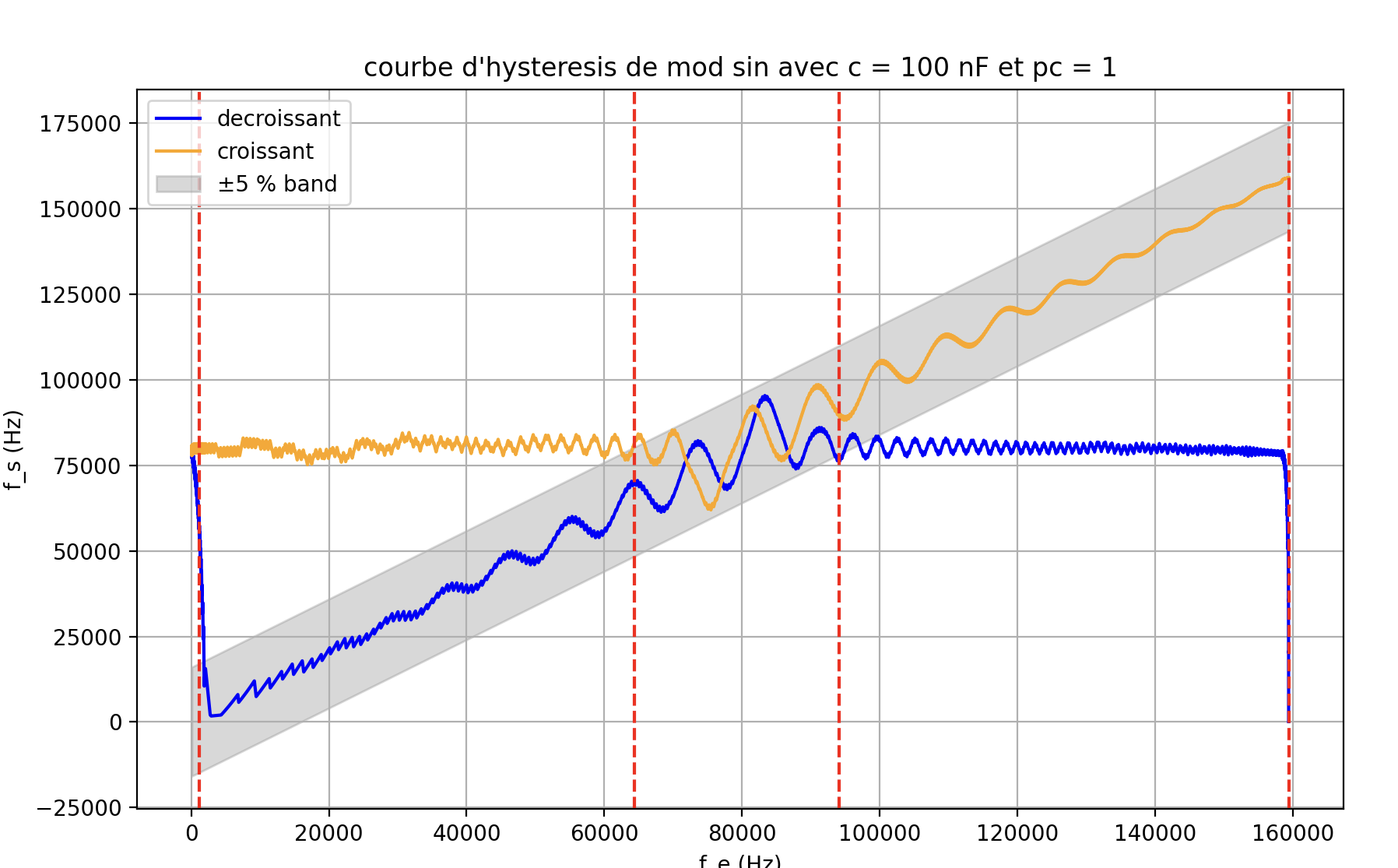
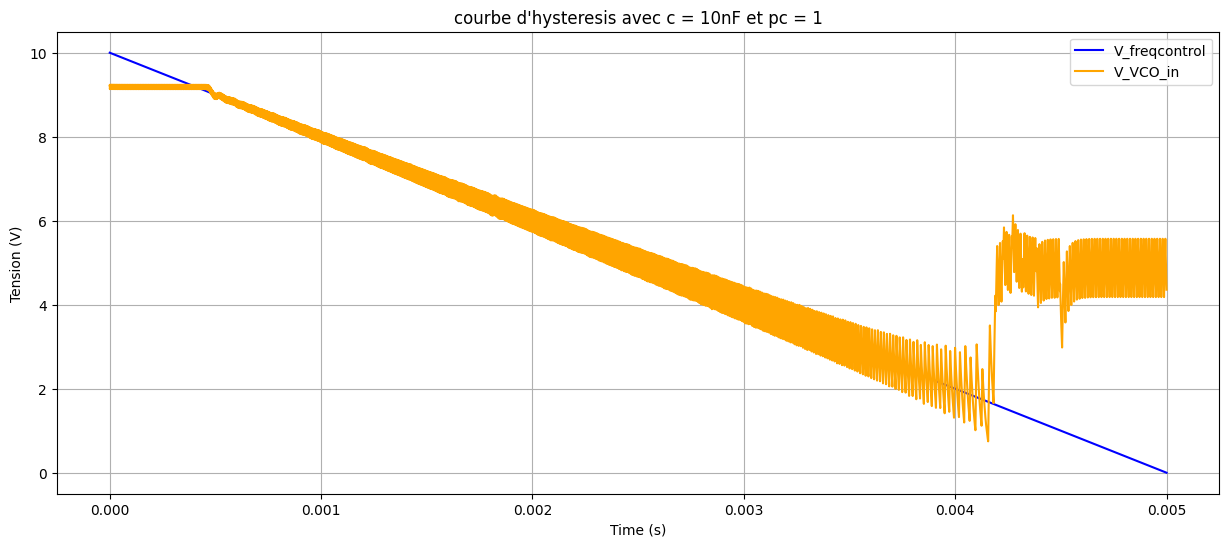
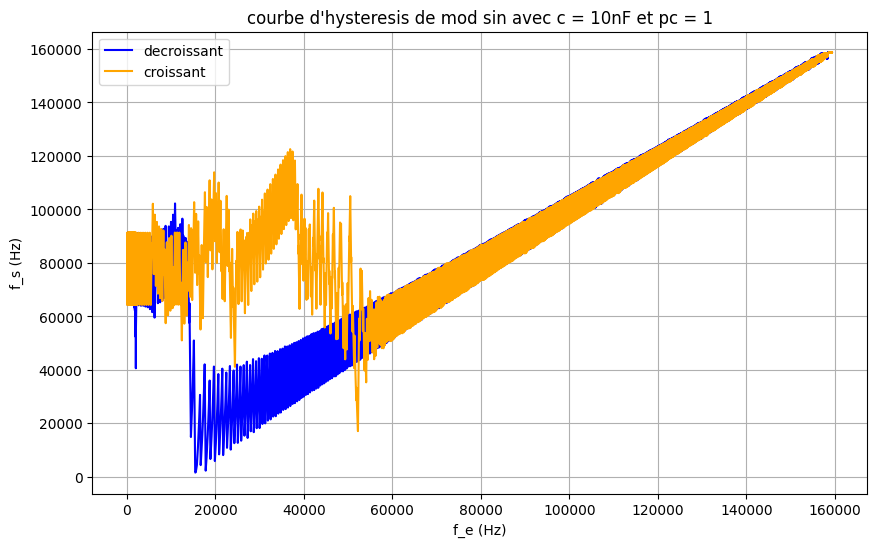
\(C_2 = 10\,\mathrm{nF}\) 时的捕获与锁定范围仿真:
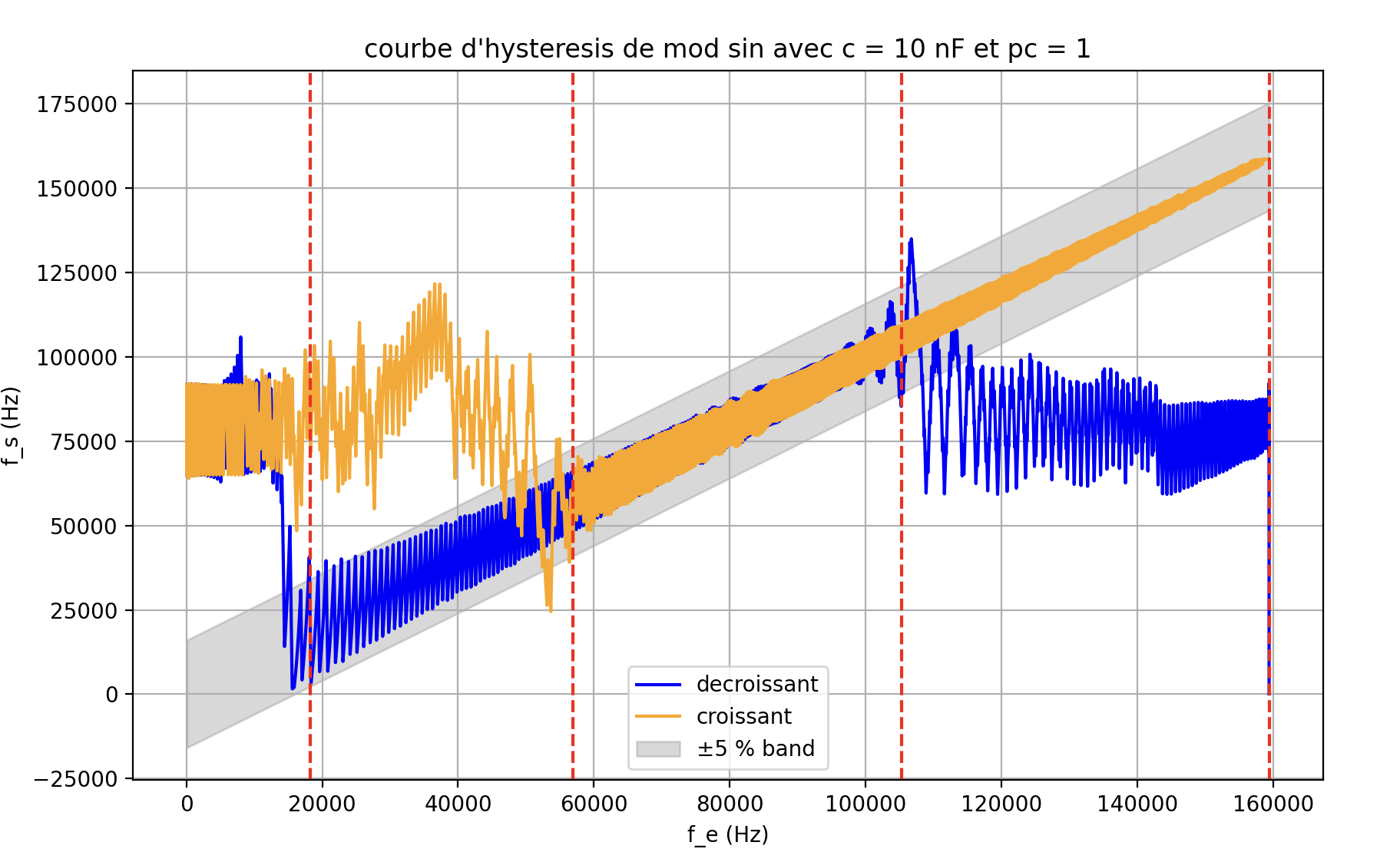
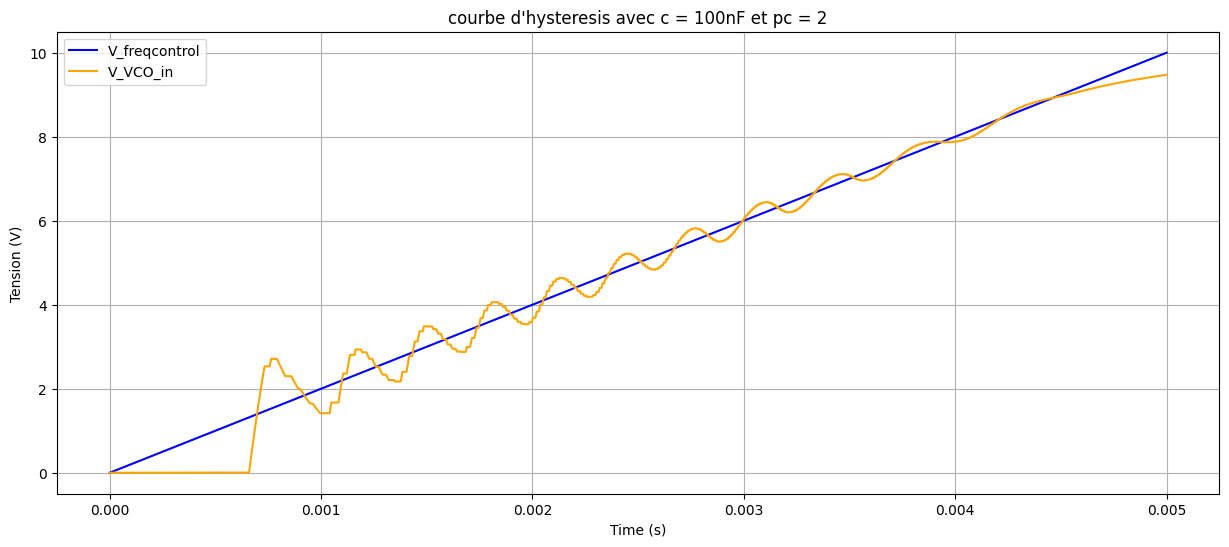
由此,对于 \(C_2 = 10\,\mathrm{nF}\),捕获范围约为 \([77\,\mathrm{kHz},\,105\,\mathrm{kHz}]\),锁定范围约为 \([19.7\,\mathrm{kHz},\,160\,\mathrm{kHz}]\);对于 \(C_2 = 100\,\mathrm{nF}\),捕获范围约为 \([65\,\mathrm{kHz},\,95\,\mathrm{kHz}]\),锁定范围约为 \([0\,\mathrm{kHz},\,160\,\mathrm{kHz}]\)。由于上升与下降过程数据异常且仿真频繁阻塞,难以解释其特性。使用 PC2 得到的唯一结果如下:
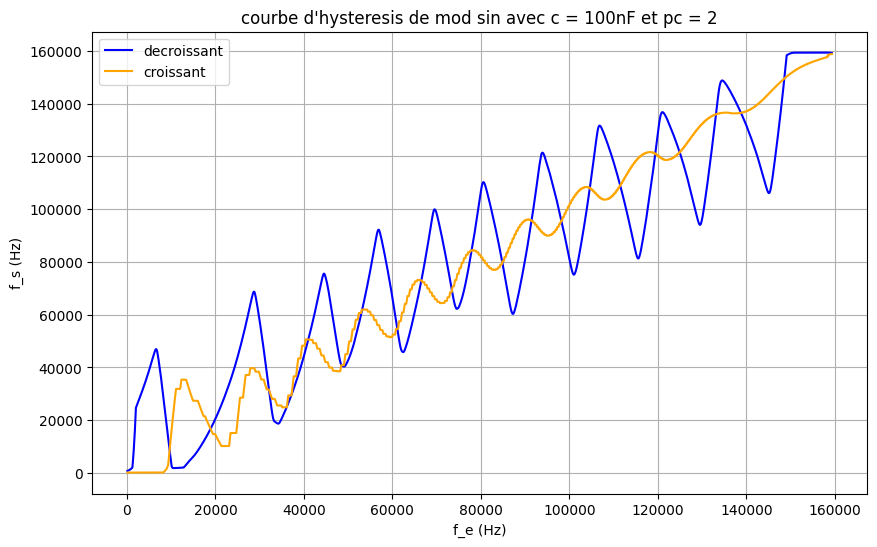
在此情况下,捕获范围与锁定范围可视为 \([0\,\mathrm{kHz},\,160\,\mathrm{kHz}]\)。
阶跃响应
仿真 CD4046B 锁相环的阶跃响应以分析动态性能。由于仿真同样阻塞,仅得 \(C_2 = 100\,\mathrm{nF}\) 且 PC1 的结果:
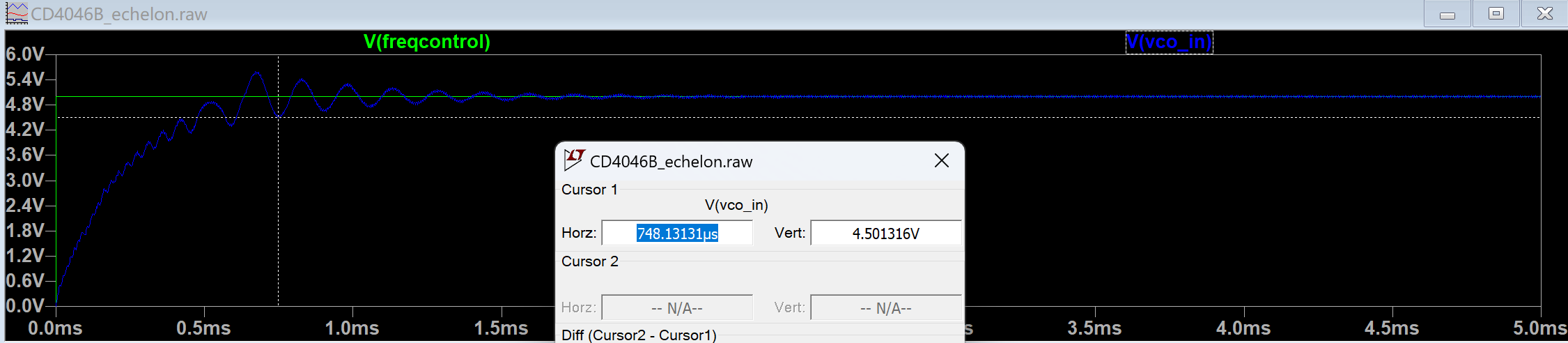
由图可知 \[ t_{10\%} = 748.13\,\mu\mathrm{s}. \] 选用一阶 RC 低通滤波器,其传递函数为 \[ H(s) = \frac{1}{1 + s\tau},\quad \tau = R_3 C_2. \] 因此 \[ \tau = 1.8\,\mathrm{k\Omega} \times 100\,\mathrm{nF} = 180\,\mu\mathrm{s}. \] 对于该滤波器,有 \[ 1 - \exp\Bigl(-\frac{t_{10\%}}{\tau}\Bigr) = 0.9 \quad\Rightarrow\quad t_{10\%} = 414\,\mu\mathrm{s}. \] 可见锁相环响应明显迟缓。
附录
工作频率范围结果
电路原理图:
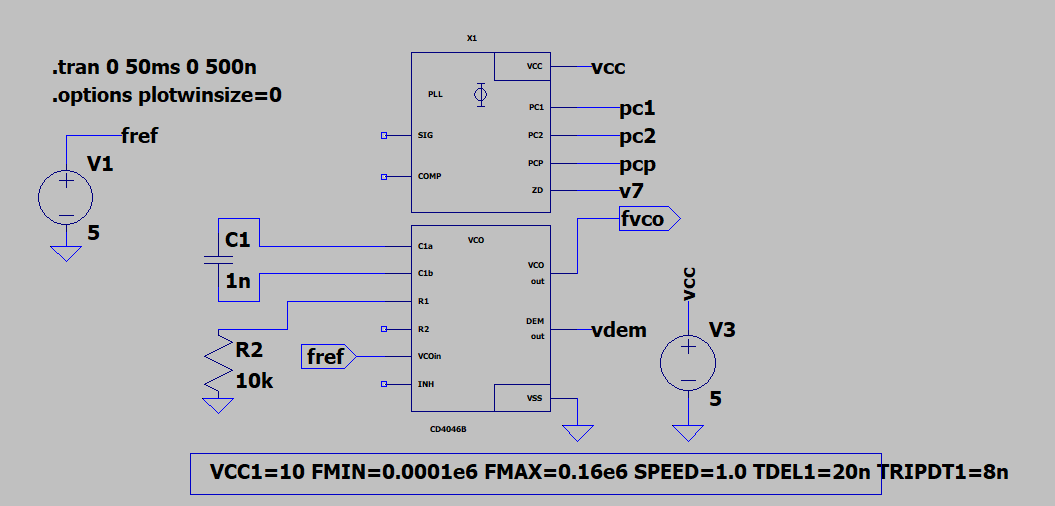
仿真结果:

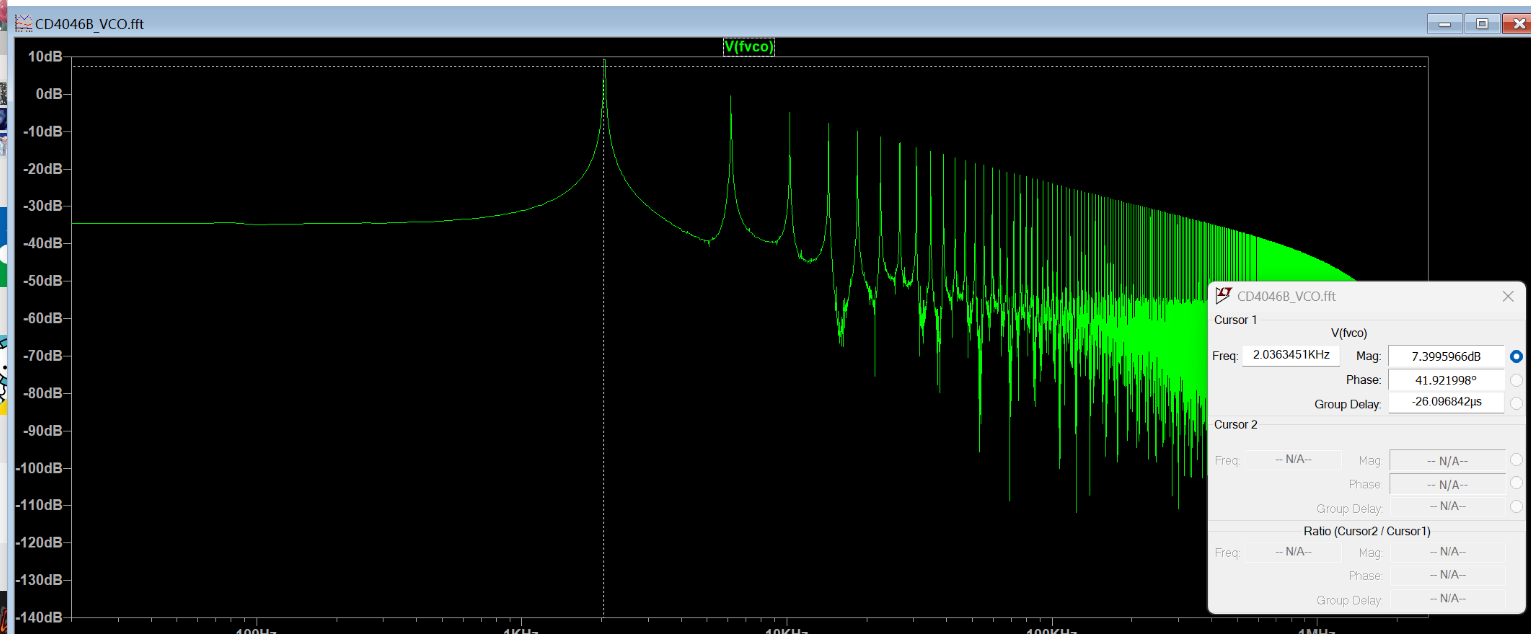
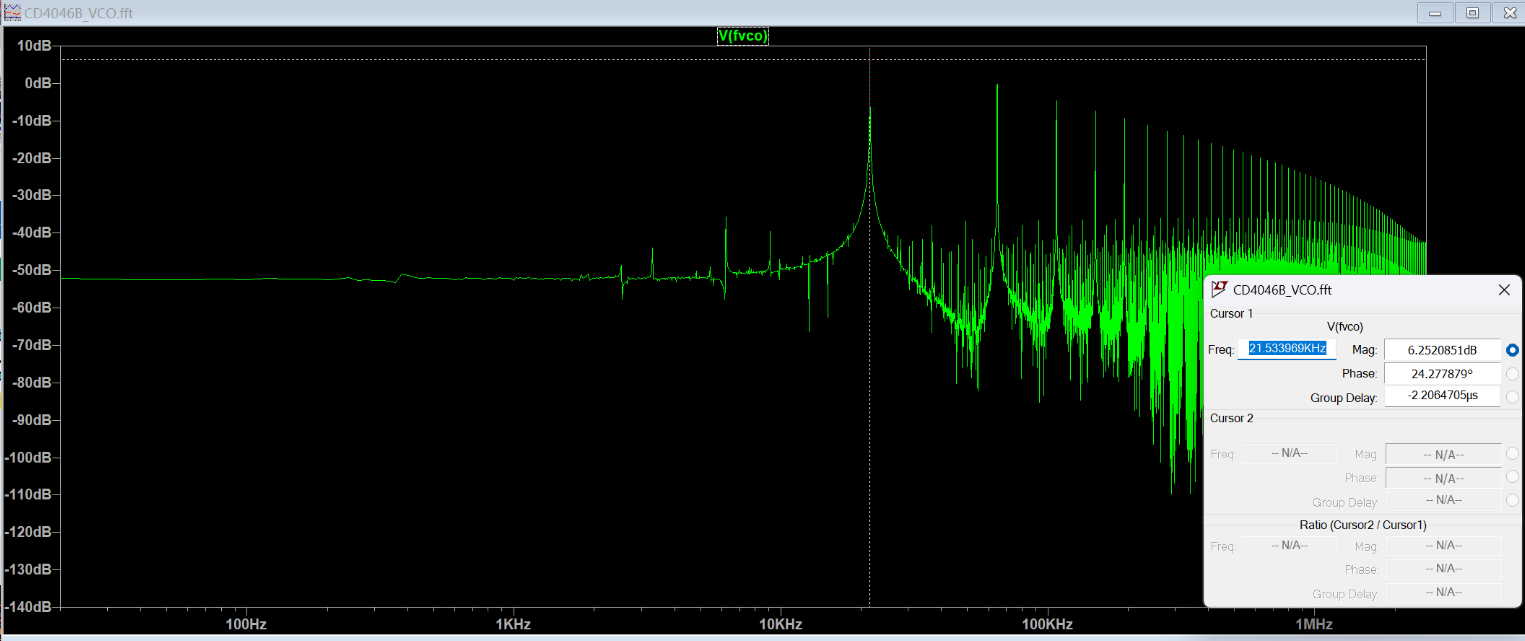
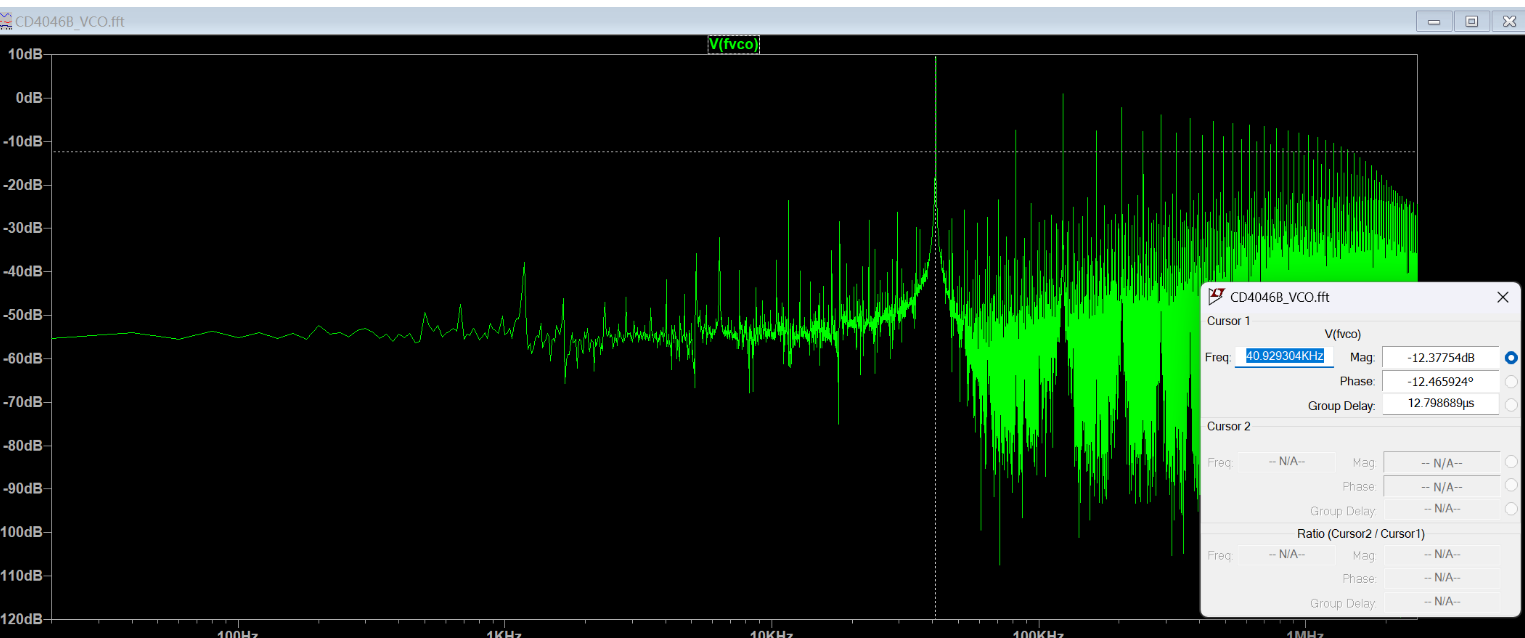
捕获范围和锁定范围结果