锁相环 Phase Locked Loop, PLL

简介

锁相环（Phase Locked Loop，PLL）是一种用于同步信号的电子电路。

它可以将输入信号的相位与参考信号的相位进行比较，并通过反馈控制来调整输出信号的频率和相位，使其与参考信号保持一致。

原理

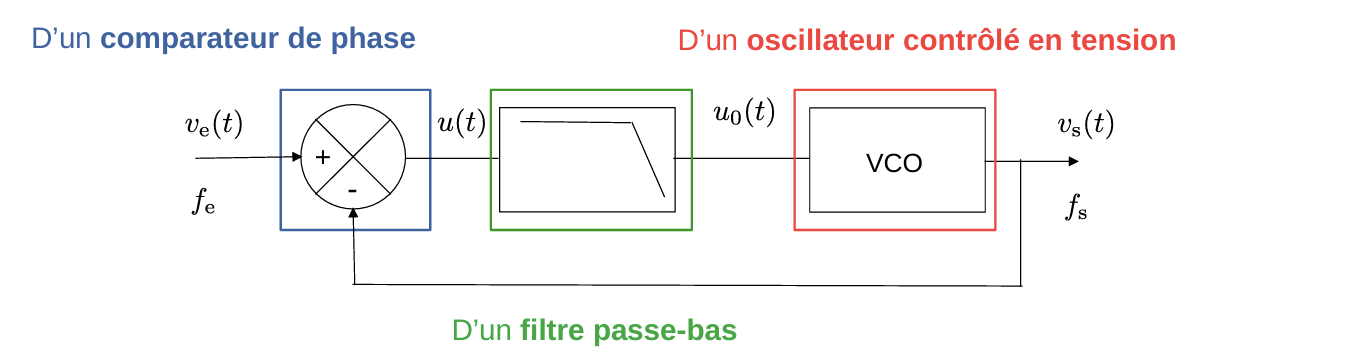
锁相环一般由一个相位比较器，一个低通绿农其和一个由电压控制的振荡器（VCO）组成。

正弦信号 正弦信号的一般形式为：$v(t)=V \sin (\phi(t))$ 频率固定时，信号可以写做：$v(t)=V \sin \left(\omega_0 t+\varphi\right)$ 如果信号频率可能随时间变化，信号可以写做：$v(t)=V \sin \left[\left(\omega_0+2 \pi f(t)\right) t\right]$ 对于两个频率不变，如果他们的$\omega_0$相等，则有它们的相位差为常数。 \[ \phi(t)=\phi_1(t)-\phi_1(t)=\left(\omega_0 t+\varphi_1\right)+\left(\omega_0 t+\varphi_2\right)=\varphi_1-\varphi_2=\text { constante } \]

如果它们的$\omega_{0,1}\neq \omega_{0,2}$，则他们的相位差为：$\phi(t)=\phi_1(t)-\phi_1(t)=\left(\omega_1-\omega_2\right) t+\left(\varphi_1-\varphi_2\right)$。其中，$(_1-_2) $被称为拍频 Battement。

相位比较器 Comparateur de phase

相位比较器的作用是比较输入信号和参考信号的相位差，并输出一个与相位差成正比的电压信号：$u=K_d g\left(\varphi_{\mathrm{e}}-\varphi_{\mathrm{s}}\right)$。

理想情况下，输出电压$u(t)$在$[-\frac{\pi}{2},\frac{\pi}{2}]$的范围内与输入信号的相位差成线性关系,超出此范围后,输出进入饱和或者周期性延拓。

比较器可以通过使参考信号和输入信号直接相乘来实现。

低通滤波器 Filtre passe-bas

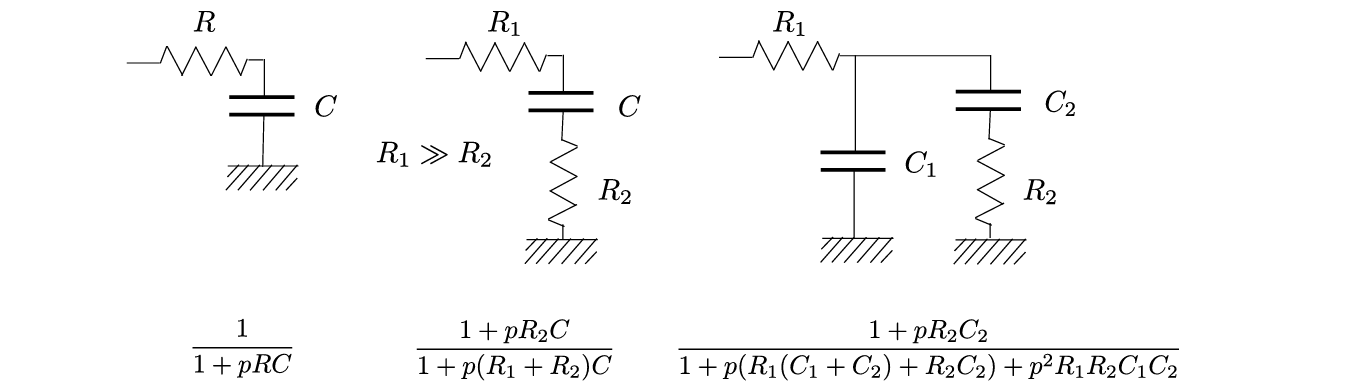
一般来说，相位比较器中通常包括了高频谐波，其中主要包括载波频率之和$f_s+f_e$和更高次分量。

我们希望使用低通滤波器仅保留电压$u(t)$的直流分量，衰减所有超出$\pm \frac \pi 2$相位范围的交流成分。

通过低通滤波器之后,输出电压更接近于比较器的理想输出电压。

电压控制振荡器 VCO

VCO是一个频率可调的振荡器，其输出频率与输入电压在一定区域内呈成线性关系，超出区域之后达到饱和。

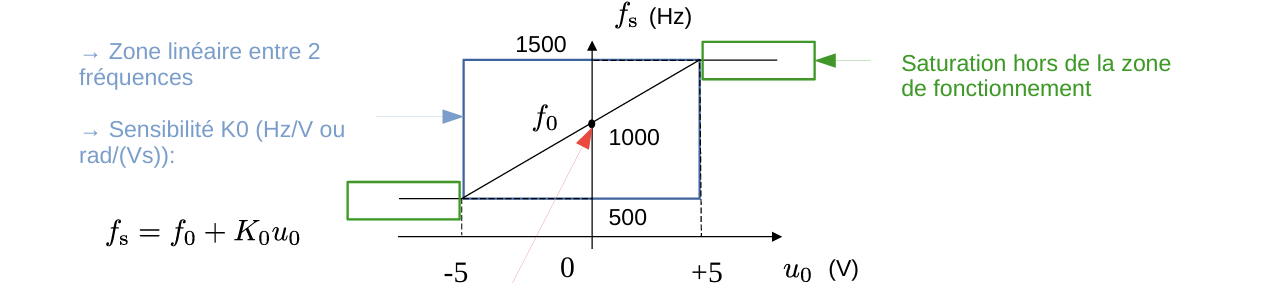
工作原理

情况1：参考输入为0

在这种情况下，VCO的输出频率为$f_0$。相位差为$\omega_0 t$，经过滤波器之后直流分量为0，系统状态保持不变。

情况1的扩展：参考输入为直流电平

与情况1同理，相位差始终为$\omega_0 t$，经过滤波器之后直流分量为0，系统状态保持不变。

情况2：参考输入为正弦信号

在这种情况下，参考输入假设为$v_e=V_e \cos \left(\omega_e t\right)$。

乘法比较器的输出为： \[ u(t)=V_e \cos \left(\omega_e t\right) \times V_s \cos \left(\omega_0 t\right)=\frac{V_e V_s}{2}\left[\cos \left(\left(\omega_e-\omega_0\right) t\right)+\cos \left(\left(\omega_e+\omega_0\right) t\right)\right] \] 经过低通滤波器之后，输出只保留差频项$cos((\omega_e-\omega_0)t)$。当差值较大时，输出仍为交流项，滤波后直流分量为0，PLL不能实现相位锁定。当$\omega_e$足够接近$\omega_0$时，差频交流成分经过环路动态作用可转化为直流控制电压，从而驱动VCO频率向$\omega_e$调节。

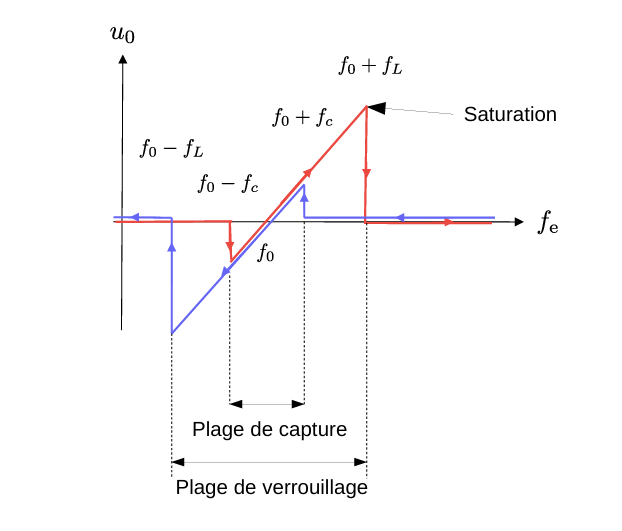
上图标出了捕获范围 Plage de capture和锁定范围 Plage de verrouillage。

捕获范围：
PLL在初始未锁定状态下，能被“捕获”并最终锁定的参考频率区间，即：
\[ f_e \in [f_0 - f_c, f_0 + f_c] \]
保持范围：
PLL在已锁定状态下，能维持锁定不被解锁的参考频率区间，即：
\[ f_e \in [f_0 - f_L, f_0 + f_L] \]
且通常有：
\[ f_L > f_c \]