Génération de signaux 信号发生器
Génération de signaux 信号发生器
简介
信号发生器（Générateur de signal）是一种能够自主产生特定电压波形（如正弦波、方波、锯齿波等）的电路，其核心工作原理基于振荡器（Oscillateur）。
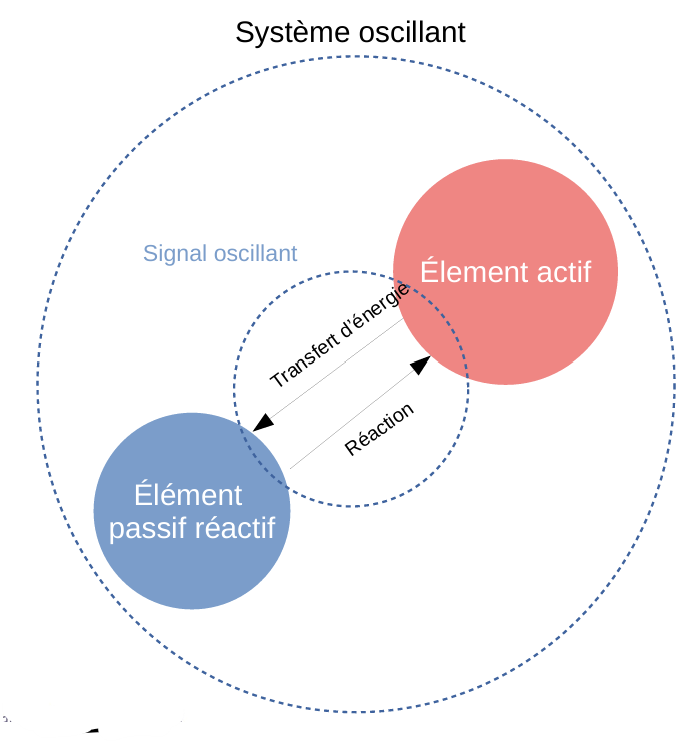
一个完整的振荡系统（Système oscillant由两个关键组件构成：
主动元件（Élément actif）：提供能量的源头，如晶体管或运算放大器，用于放大或补偿能量损耗。
被动反应元件（Élément passif réactif）：通常由电感（L）、电容（C）或电阻（R）组成，用于储存和释放能量，控制频率特性。
这两者之间形成能量的转移和反应，从而维持持续的振荡。
两类常见的振荡器：
线性振荡器（Oscillateurs linéaires/sinusoïdaux）：如RC、LC或石英振荡器，产生的是连续波形（例如正弦波）。
弛张振荡器（Oscillateurs à relaxation）：例如施密特触发器或多谐振荡器，输出的是非连续的波形（例如方波、锯齿波），原理是能量储存与突释放的循环
正弦振荡器 Oscillateurs sinusoïdaux
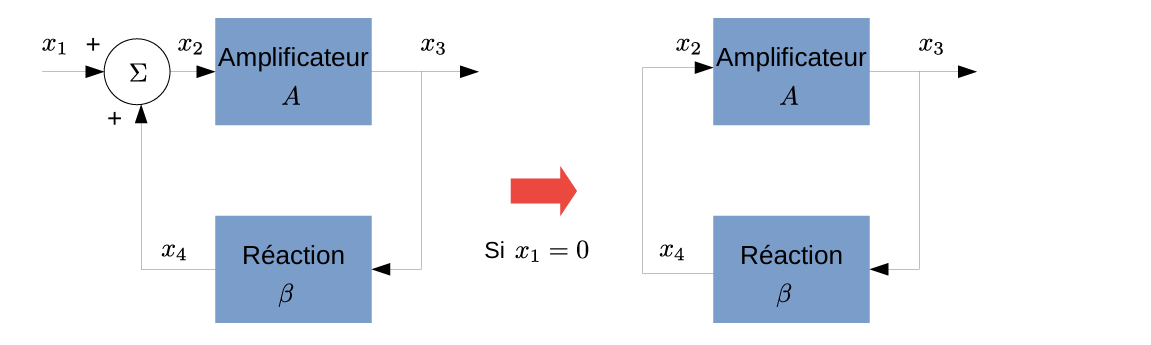
振荡器由一个放大器和一个反馈网络组成。如果希望系统无外部输入即可持续震荡，必须满足：
- 反馈为正 （contre-réaction positive）
- 放大器增益\(A\)与反馈网络传递函数\(\beta(j\omega)\)满足一定关系。
假设A在频率上恒定，则系统的传递函数：
\[ H(j \omega)=\frac{x_3}{x_1}=\frac{A}{1-A \beta(j \omega)} \]
振荡器的三种工作状态
根据\(A\)和\(\beta(j\omega)\)的关系，可将振荡器的工作状态分为三类:
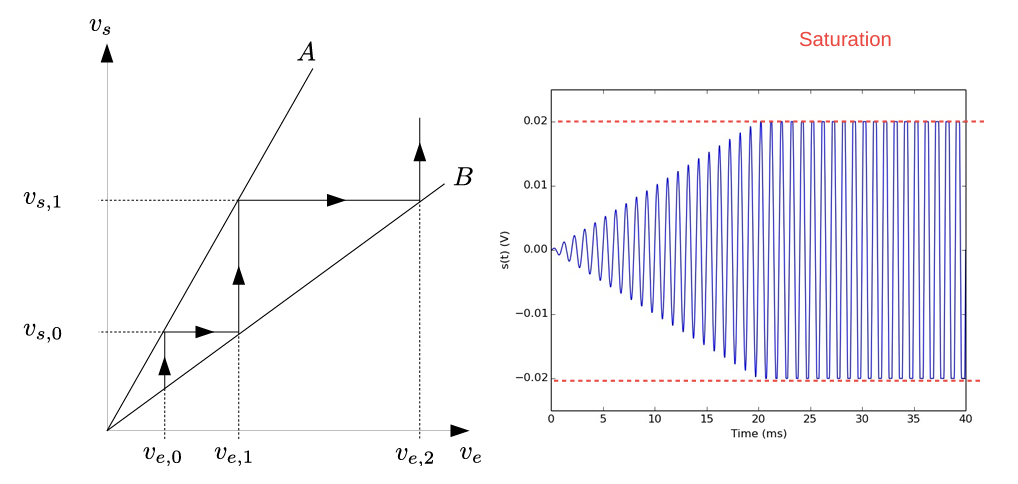
- 增益反馈过强： \(A \beta(j \omega) >
1\)，系统不稳定，输出信号会无限增大，直到饱和。但其非线性特性也可以用在方形信号发生器中。
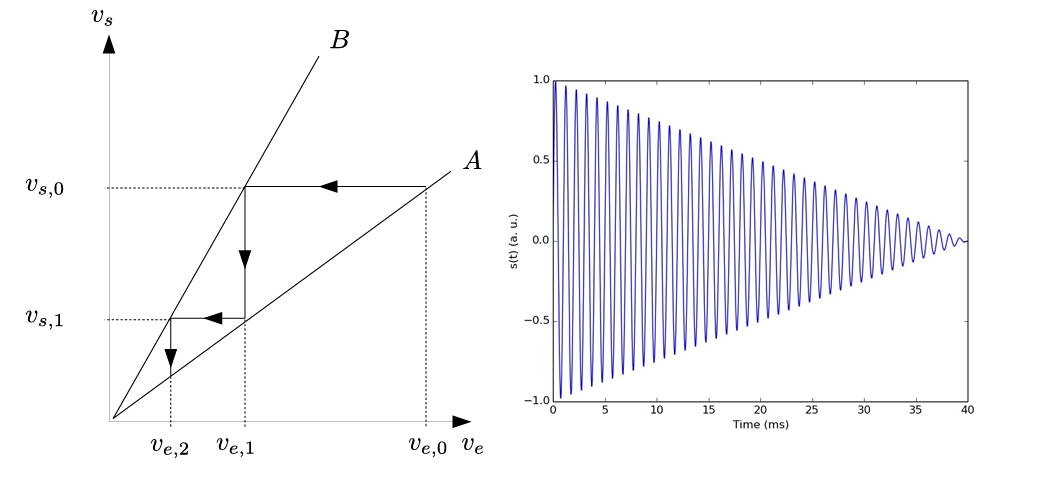
- 增益反馈不足： \(A \beta(j \omega) <
1\)，系统稳定，输出信号会衰减到0。
- 增益反馈适中： \(A \beta(j \omega) =
1\)，系统处于临界状态，输出信号保持恒定幅度。可以用来构建正弦振荡器（线性振荡器）
巴克豪森条件和震荡频率
为了使得电路持续自激振荡，需要满足以下条件： \[ 1-A \beta(j \omega)=0 \Longleftrightarrow A \beta(j \omega)=1 \]
换言之：
\[ |A \beta(j \omega)|=1 \quad \text { 且 } \quad \varphi(A \beta(j \omega))=2 n \pi, \quad n \in \mathbb{N} \]
振荡频率\(f_0\)是使得贿赂相位为\(n\pi\)的频率点。即： \[ \beta\left(j \omega_0\right) \in \mathbb{R} \Leftrightarrow \varphi\left(\beta\left(j \omega_0\right)\right)=n \pi, n \in \mathbb{N} \] 也就是说，震荡频率由反馈网络确定。此时，增益应该满足： \[ A=\frac{1}{\left|\beta\left(j \omega_0\right)\right|} \]
因此，反馈电路应该满足幅度和相位为频率的函数，并且通过相位应该为0或\(\pm\pi\)。
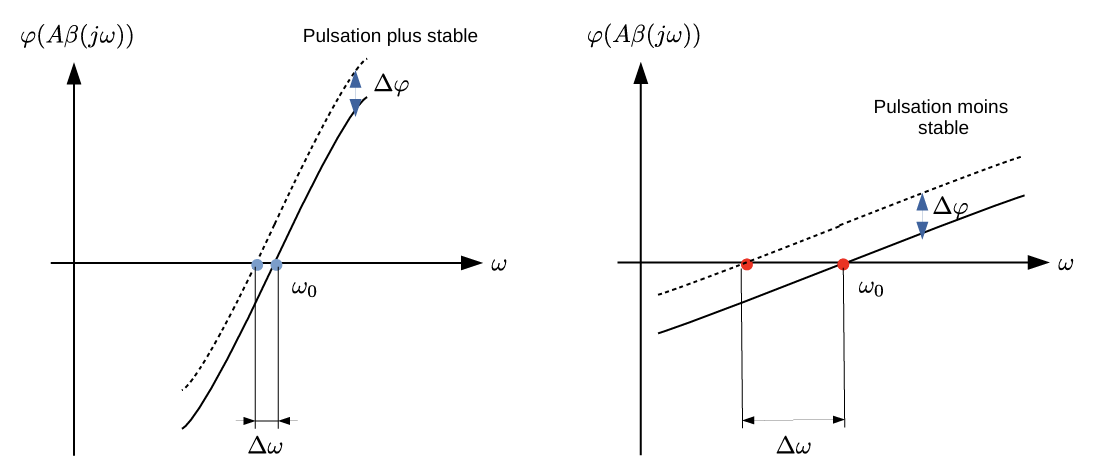
频率稳定性
振荡器通常是实现成本和振荡频率稳定性的折中考虑。
频率稳定性一般定义为：
\[ S\left(\omega_0\right)=\left|\frac{d \varphi(\beta(j \omega))}{d\left(\omega / \omega_0\right)}\right|_{\omega=\omega_0} \]
即相位在振荡频率周围的变化越大，振荡器越稳定。
对于一个使用二阶带通滤波器实现的振荡器的反馈电路，其传递函数为：
\[ H_{B P 2}(s)=K \frac{s \frac{\omega_0}{Q}}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} \]
此时，频率稳定性为：\(S(\omega_0) = 2Q\)。
CR移相振荡器
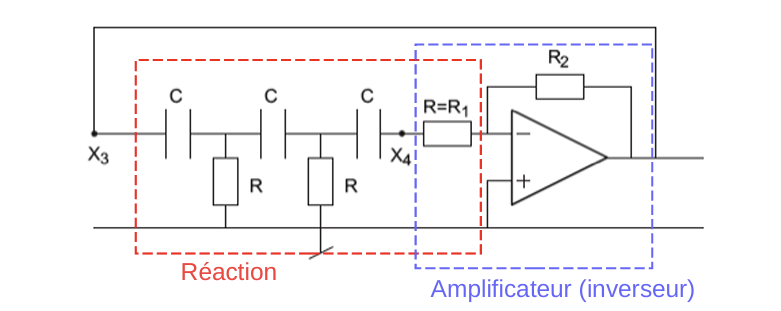CR移相振荡器由以下两个部分组成：
一个反相放大器（Amplificateur inverseur）
一个由三个CR单元组成的反馈电路（三级高通结构）
其反馈电路传递函数为：
\[ \beta(j \omega)=\frac{1}{1-\frac{5}{(\omega R C)^2}-j\left(\frac{6}{\omega R C}-\frac{1}{(\omega R C)^3}\right)} \]
这里进行简要证明：
节点定义
电路中共有四个节点 (node)：
- 输入节点：设输入电压为 \(V_0\)；
- 两个中间节点：分别为 \(V_1\) 和 \(V_2\)；
- 输出节点：输出电压为 \(V_3\)。
因此有 \(\beta = V_3 / V_0\)。基尔霍夫定律 (Kirchhoff’s laws) 建立方程
令 \(x = j\omega RC\)，根据基尔霍夫电流定律 (KCL)，可得：
\[ \begin{cases} (1 + 2x)\,V_1 - x\,V_2 = x\,V_0, \\[6pt] x\,V_1 - (1 + 2x)\,V_2 + x\,V_3 = 0, \\[6pt] x\,V_2 - (1 + x)\,V_3 = 0. \end{cases} \]以下以节点 \(V_1\) 的方程推导为例，其余节点同理。
节点 \(V_1\) 的电流分析
节点 \(V_1\) 有三条支路：
- 左侧电容分支：电流记为 \(I_1\)；
- 右侧电容分支：电流记为 \(I_2\)；
- 下方电阻分支：电流记为 \(I_3\)。根据电容电流公式及拉普拉斯变换：
\[ I_1 = C\frac{d(V_1 - V_0)}{dt} \quad\xrightarrow{\mathcal{L}}\quad I_1 = j\omega C\,(V_1 - V_0), \]
同理：
\[ I_2 = j\omega C\,(V_1 - V_2), \quad I_3 = \frac{V_1}{R}. \]
由基尔霍夫电流定律：
\[ I_1 + I_2 + I_3 = 0, \]
即
\[ \frac{V_1}{R} + j\omega C\,(V_1 - V_0) + j\omega C\,(V_1 - V_2) = 0. \]
令 \(x = j\omega RC\)，即可化简为第一条方程。对其他节点重复相同过程，可得第二、三条方程。
矩阵形式与求解 将上述线性方程组写成矩阵形式：
\[ \begin{pmatrix} 1+2x & -x & 0 \\ x & -(1+2x) & x \\ 0 & x & -(1+x) \end{pmatrix} \begin{pmatrix} V_1 \\ V_2 \\ V_3 \end{pmatrix} = \begin{pmatrix} x\,V_0 \\ 0 \\ 0 \end{pmatrix}. \]
解得：
\[ V_3 = \frac{x^3}{x^3 + 6x^2 + 5x + 1}\,V_0, \quad \beta = \frac{V_3}{V_0} = \frac{x^3}{x^3 + 6x^2 + 5x + 1}. \]替换 \(x = j\omega RC\)** 最后令 \(x = j\omega RC\)，得到：
\[ \beta(j\omega) = \frac{1} {1 - \frac{5}{(\omega RC)^2} - j\Bigl(\frac{6}{\omega RC} - \frac{1}{(\omega RC)^3}\Bigr)}. \]
性能指标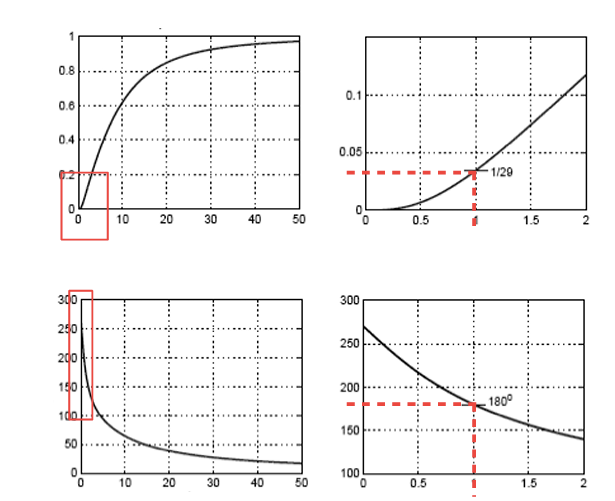 
- 振荡频率：\(f_0=\frac{1}{2 \pi \sqrt{6} R
C}\) - 频率稳定性：\(S\left(\omega_0\right)=\frac{12}{29} \sqrt{6}
\approx 1.01\) - 起振条件：\(A=-\frac{R_2}{R_1}=-29\)
