filtre 滤波器
filtre 滤波器
概述
滤波器用以选择性地通过或阻止信号的频率成分,以及删除信号中的噪声。
按照频率响应特性,滤波器可分为低通(Filtre passe-bas)、高通(Filtre passe-haut)、带通(Filtre passe-bande)和带阻(Filtre coupe-bande)滤波器。
按照不同的技术,可分为电子滤波器和机械与物理滤波器。
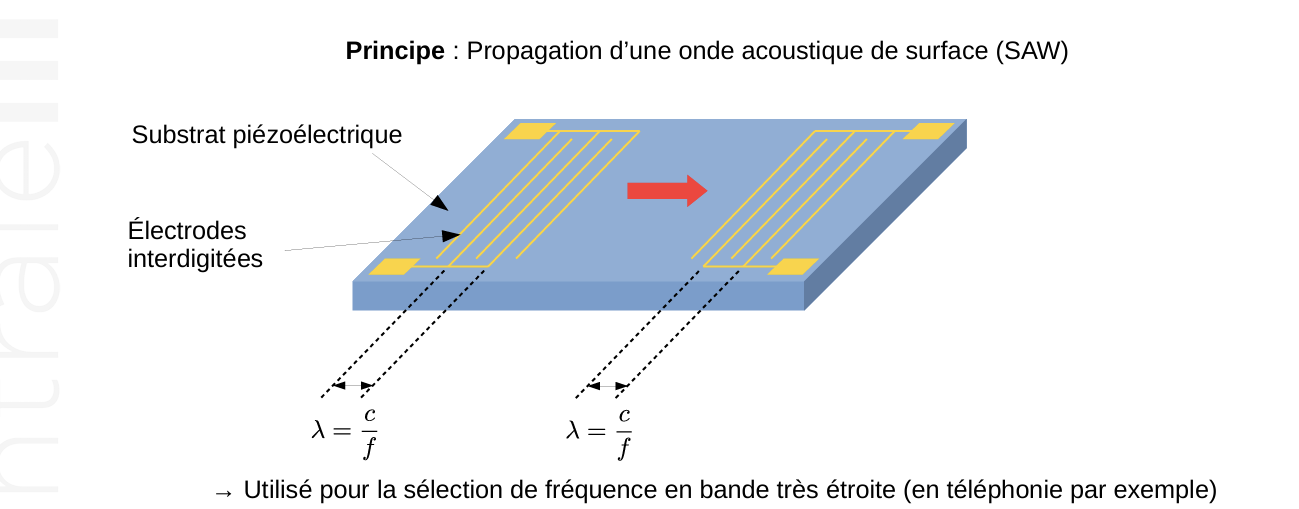
> 图为表面声波滤波器(SAW
Filter)。当一个射频信号加在左侧交指电极上时,会激励出沿压电材料表面传播的表面声波。表面声波在材料表面传播的波长满足公式\(\lambda =
c/f\)。由于电极之间的间距固定(决定了某一波长),只有特定频率的声波能有效激发与接收,因此实现了对信号频率的窄带选择性滤波。不符合频率条件的信号将不会有效传播或被转换,从而被抑制。
理想滤波器是指不引起信号失真的滤波器,其作用仅是放大或延迟信号,而不改变信号的频谱结构。
理想滤波器在现实中不存在!
滤波器的传递函数
在频域上,滤波器的传递函数\(H(f)\)是输入信号\(X(f)\)和输出信号\(Y(f)\)的比值:\(Y(p) = H(p)X(p)\)。
对于一个线性滤波器,其传递函数可以写作:
\[ H(p)=\frac{\sum_{i=0}^k b_i p^i}{\sum_{j=0}^m a_j p^j} \]
与之前课程中提到的传递函数相同,一个线性系统仅当其所有极点的实部为负时才稳定。
渐进行为 考虑上述传递函数在低频和高频时的渐进。
在低频时,\(H(0)\to\frac{b_0}{a_0}\)
在高频时: - \(H(j \omega) \rightarrow \frac{b_k}{a_m}(j \omega)^{k-m}\) - 模长 \(|H(j \omega)| \rightarrow\left|\frac{b_k}{a_m}\right| \omega^{k-m}\) - 相位 \(\varphi(H(j \omega)) \rightarrow n \frac{\pi}{2}\)
正则传递函数
一阶滤波器
低通滤波器: \(H_{L P}(j \omega)=K \frac{1}{1+j \frac{\omega}{\omega_0}} \ or \ H_{L P}(s)=K \frac{\omega_0}{\omega_0+s}\)
高通滤波器: \(H_{H P}(j \omega)=K \frac{j \frac{\omega}{\omega_0}}{1+j \frac{\omega}{\omega_0}} \ or \ H_{H P}(s)=K \frac{s}{\omega_0+s}\)
二阶滤波器
\[ \begin{array}{ll} H_{L P 2}(j \omega)=K \frac{1}{1+2 \xi j \frac{\omega}{\omega_0}-\left(\frac{\omega}{\omega_0}\right)^2} & H_{L P 2}(s)=K \frac{\omega_0^2}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} \\ H_{H P 2}(j \omega)=K \frac{-\left(\frac{\omega}{\omega_0}\right)^2}{1+2 \xi j \frac{\omega}{\omega_0}-\left(\frac{\omega}{\omega_0}\right)^2} & H_{H P 2}(s)=K \frac{s^2}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} \\ H_{B P 2}(j \omega)=K \frac{2 \xi j \frac{\omega}{\omega_0}}{1+2 \xi j \frac{\omega}{\omega_0}-\left(\frac{\omega}{\omega_0}\right)^2} & H_{B P 2}(s)=K \frac{s \frac{\omega_0}{Q}}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} \\ H_{B S 2}(j \omega)=K \frac{1-\left(\frac{\omega}{\omega_0}\right)^2}{1+2 \xi j \frac{\omega}{\omega_0}-\left(\frac{\omega}{\omega_0}\right)^2} & H_{B S 2}(s)=K \frac{s^2+\omega_0^2}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} \end{array} \]
其中,复频率\(s=jω\),品质因数\(Q=\frac{1}{2\xi}\)。
滤波器设计
gabarit 滤波器模板
滤波器的“gabarit”(模板曲线)是用于定义其性能指标的图形工具,通常在频率响应图中标出不同区域的允许误差范围和性能要求。
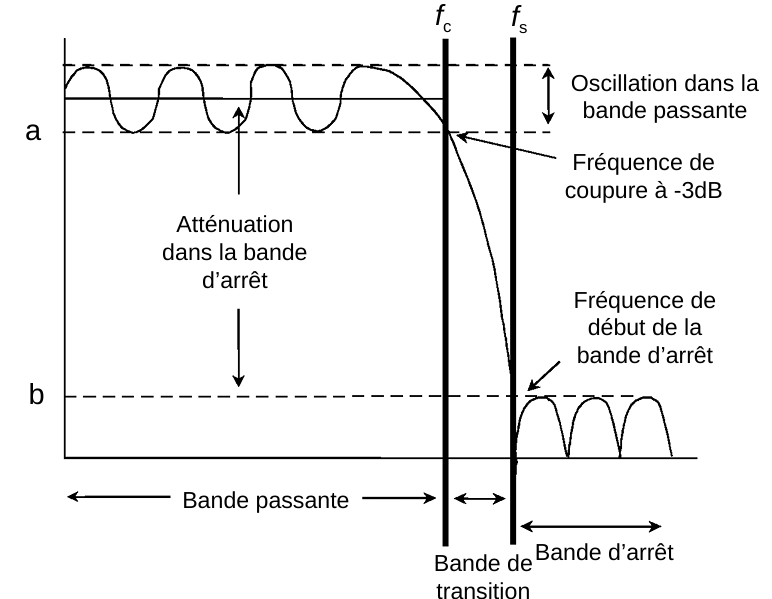
关键参数
\(f_c\):-3dB截止频率(频率响应下降3dB处)。
\(f_s\):阻带起始频率(定义阻带的开始)。
带通区(Bande passante):滤波器主要工作频率范围,信号能无明显衰减通过。
带阻区(Bande d’arrêt):需要抑制的频率范围,信号被大幅衰减。
过渡带(Bande de transition):从通带过渡到阻带的区域,滤波器特性快速变化。
阻带衰减(Atténuation dans la bande d’arrêt):表示滤波器在阻带中抑制信号的能力。
通带波动(Oscillation dans la bande passante):通带内的增益可能不是完全平坦,会存在微小起伏。
a、b 水平线:定义了通带最大增益与阻带最大允许增益,称为“模板边界”。
- a:通带最大增益。
- b:阻带最大允许增益。
模板边界用于明确滤波器性能要求,通常在频率响应图中标出。
设计方法
编写技术指标(Cahier des charges)
归一化与转换:将实际问题转换为标准归一化低通滤波器(Passe-bas normalisé, PBN)问题。
选择响应类型 根据需求选择滤波器响应特性:
Butterworth(平滑响应,无波纹)
Chebyshev(具有通带或阻带波纹,过渡带更陡)
Bessel(群延迟最小,保形性好)
选择电路结构
被动结构(passif):仅使用电感、电容、电阻
有源结构(actif):含运算放大器等有源元件
多项式确定:使用标准表格(1阶和2阶)确定归一化低通滤波器的传递函数 \[ H_{L P N}(S)=\prod_i \frac{\left|s_i\right|^2}{\left(S-s_i\right)\left(S-\overline{s_i}\right)} \]
反归一化,计算实际的传递函数形式
确定电路结构:选择合适的电路拓扑结构(如Sallen-Key、Biquad等)。
确定电路元件参数:电感、电容和电阻的值
滤波器的归一化
将各种不同类型的滤波器统一转化为标准低通滤波器(PBN)进行分析,从而简化设计与计算。
PBN的传递函数应该为:
\[ H_{P B N}(S)=\prod_i \frac{\left|s_i\right|^2}{\left(S-s_i\right)\left(S-\overline{s_i}\right)} \]
低通滤波器
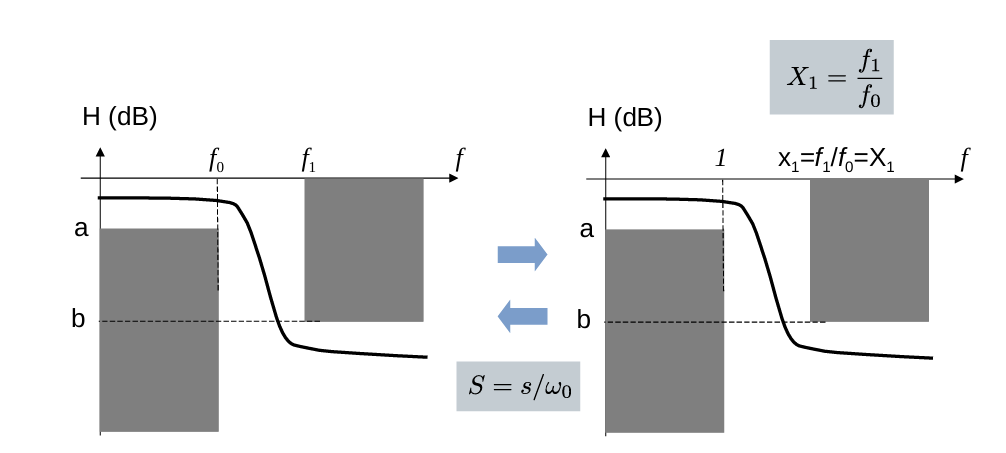
归一化操作将滤波器的截止频率\(f_0\)映射为1,其余频率按比例缩放。具体公式为:
\[ S = \frac{s}{\omega_0}, \quad X_1 = \frac{f_1}{f_0} \]
映射后,截止频率为1,带阻起始频率为\(X_1\)。
高通滤波器
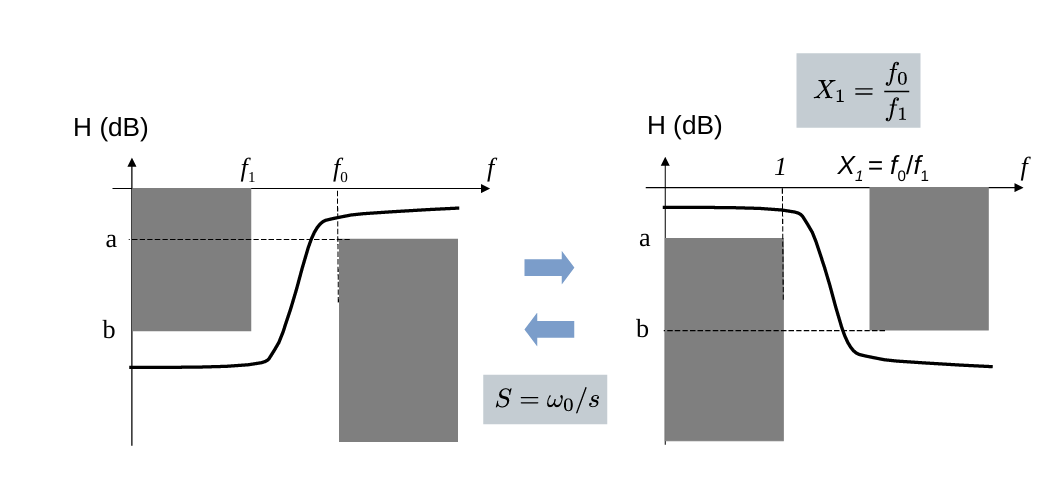
与低通滤波器类似。具体公式为: \[ S = \frac{\omega_0}{s}, \quad X_1 = \frac{f_0}{f_1} \]
通过将\(p替换为\frac{\omega_0}{p}\),可以实现高通滤波器和低通滤波器互换。
\[ H(p)=\frac{\left(\frac{p}{\omega_0}\right)^2}{1+\left(\frac{p}{Q \omega_0}\right)+\left(\frac{p}{\omega_0}\right)^2} \quad \stackrel{p \Rightarrow \frac{\omega_0}{p}}{\longrightarrow} \quad H(p)=\frac{1}{1+\frac{p}{Q}+p^2} \]
带通滤波器
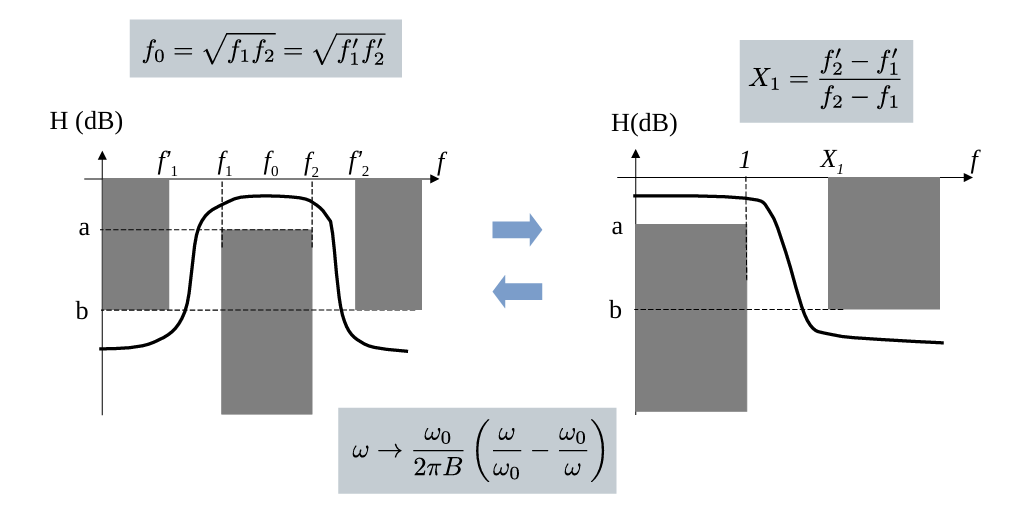
需要同时考虑两个截止频率\(f_1\)和\(f_2\),其中心频率为:
\[ f_0 = \sqrt{f_1 f_2} = \sqrt{f_1'f_2'} \]
带宽标准化变换公式为:
\[ \omega \to \frac{\omega_0}{2\pi B} \left( \frac{\omega}{\omega_0} - \frac{\omega_0}{\omega} \right) \]
其中,带宽\(B\)为:
\[ B = f_2 - f_1 \]
归一化后截止频率为:
\[ X_1 = \frac{f_2' - f_1'}{f_2 - f_1} \]
归一化低通滤波器的阶数为\(n\),对应的带通滤波器的阶数为\(2n\)。
带阻滤波器 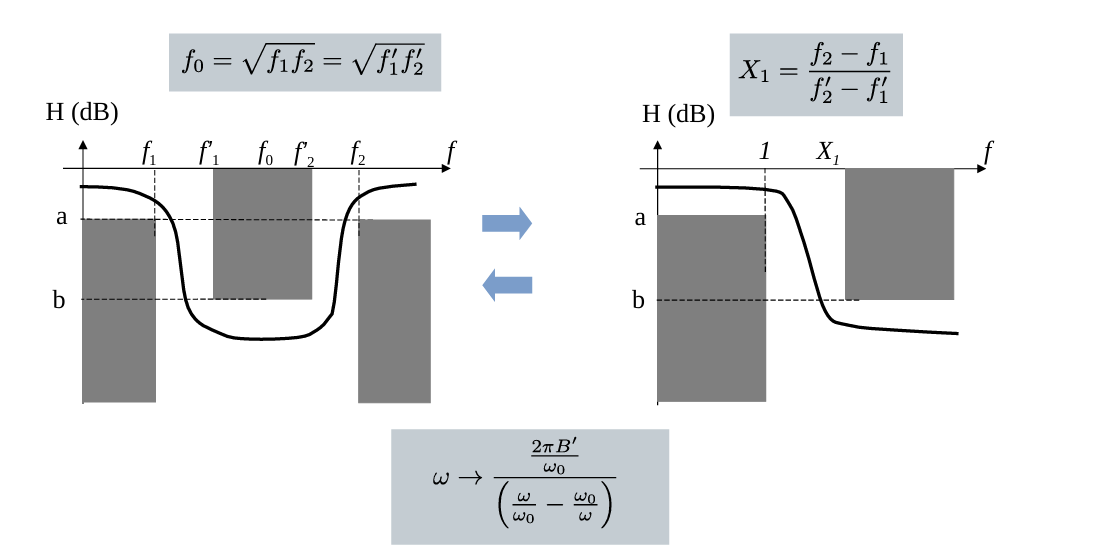
带阻滤波器的归一化与带通滤波器类似。公式为:
\[ \begin{gathered} f_0=\sqrt{f_1 f_2} \\ \omega \rightarrow \frac{2 \pi B^{\prime}}{\omega_0} \cdot\left(\frac{\omega}{\omega_0}-\frac{\omega_0}{\omega}\right)^{-1} \\ X_1=\frac{f_2-f_1}{f_2^{\prime}-f_1^{\prime}} \end{gathered} \]
响应类型的选择
巴特沃斯滤波器(Filtre de Butterworth) \[ H(p)=\frac{K}{1+(-1)^n p^{2 n}} \]
在零频处增益最大;
通带中保持最大平坦度(critère de méplat),无波动;
衰减随频率单调增加。
切比雪夫滤波器(Filtre de Chebyshev)
\[ |H(\omega)|^2=\frac{1}{1+\varepsilon^2 T_n^2(\omega)} \begin{cases}T_n(x)=\cos (\arccos x) & \mathrm{x} \leq 1 \\ T_n(x)=\operatorname{ch}(\arg \operatorname{ch} x) & \mathrm{x}>1\end{cases} \]
通带中允许等波纹(ripples)
相比Butterworth,过渡带更陡峭,选择性更强;
衰减速度快于Butterworth,但不平坦。
贝塞尔滤波器(Filtre de Bessel)
\[ H(p) \approx e^{-p} \quad \longrightarrow \quad H(p)=\frac{1}{B_n(p)} \]
- 最为线性的相位响应,适用于对相位敏感的应用。
| 类别 | 巴特沃斯滤波器(Butterworth) | 切比雪夫滤波器(Chebyshev) | 贝塞尔滤波器(Bessel) |
|---|---|---|---|
| 优点 | - 通带内响应曲线非常平坦 - 良好的传播时间特性 - 计算简便 |
- 对于同阶滤波器,具有最陡峭的截止特性 | - 在给定阶数下,通带内相位最线性 |
| 缺点 | - 截止陡峭程度中等 - 归一化通带内衰减固定为 -3dB |
- 通带内存在波动 - 通带传播时间依赖于频率 |
- 截止陡峭性差 |
| 阶数计算 | \(n \ge \dfrac{\ln \left(10^{b/10} - 1 \right)}{2 \ln(X_1)}\) | \(n \ge \dfrac{\cosh^{-1} \left( \sqrt{\dfrac{10^{b/10} - 1}{10^{a/10} - 1}} \right)}{\cosh^{-1}(X_1)}\) | — |
| 应用 | - 测量设备(如电压表) | - 抑制靠近有用信号频率的干扰信号 | - 信号传输系统 |
有源/无源滤波器
| 无源滤波器(Filtres passifs) | 有源滤波器(Filtres actifs) | |
|---|---|---|
| 组件 | 使用 R、L、C:体积大、昂贵、调节困难 | R、C 即可:体积小、成本低、易于集成与调节 |
| 增益 | 无放大功能,Q 值较低 | 可放大,Q 值更高 |
| 负载依赖性 | 滤波器特性依赖于负载 | 滤波器特性与负载无关 |
| 电源 | 不需要电源 | 必须要有电源 |
| 噪声性能 | 被动元件噪声小 | 有源器件可能带来噪声干扰 |
| 对元件的敏感性 | 对元件变化不太敏感(低或中) | 对元件变化更敏感 |
有源滤波器结构
Structure Biquad 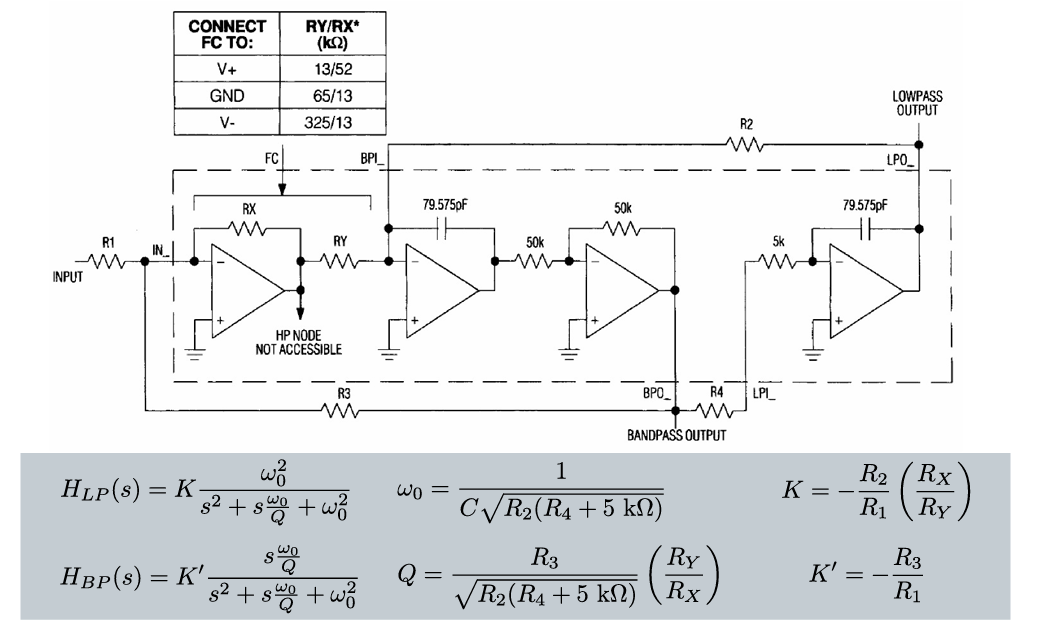
\[ \begin{array}{llc} H_{L P}(s)=K \frac{\omega_0^2}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} & \omega_0=\frac{1}{C \sqrt{R_2\left(R_4+5 \mathrm{k} \Omega\right)}} & K=-\frac{R_2}{R_1}\left(\frac{R_X}{R_Y}\right) \\ H_{B P}(s)=K^{\prime} \frac{s \frac{\omega_0}{Q}}{s^2+s \frac{\omega_0}{Q}+\omega_0^2} & Q=\frac{R_3}{\sqrt{R_2\left(R_4+5 \mathrm{k} \Omega\right)}}\left(\frac{R_Y}{R_X}\right) & K^{\prime}=-\frac{R_3}{R_1} \end{array} \]
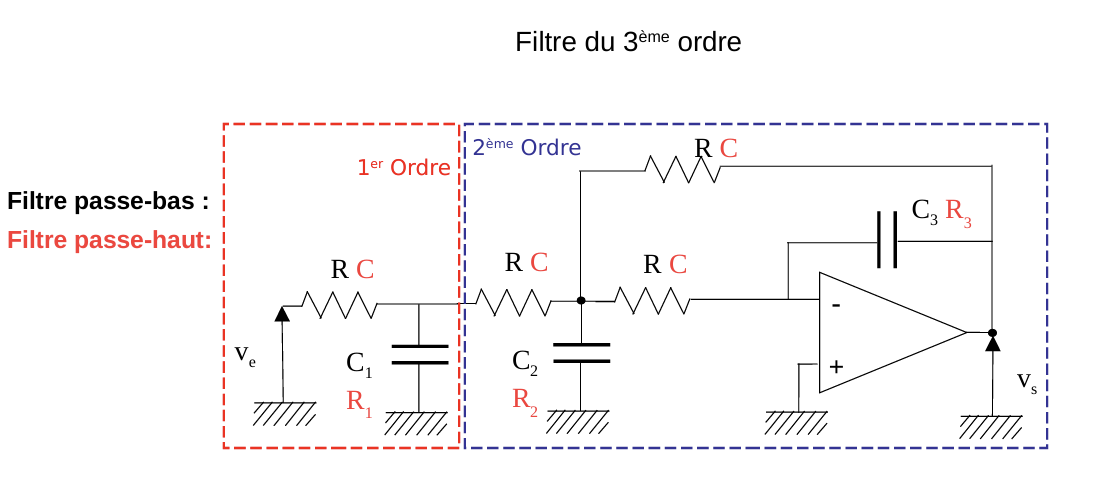
Structure Sallen-Key
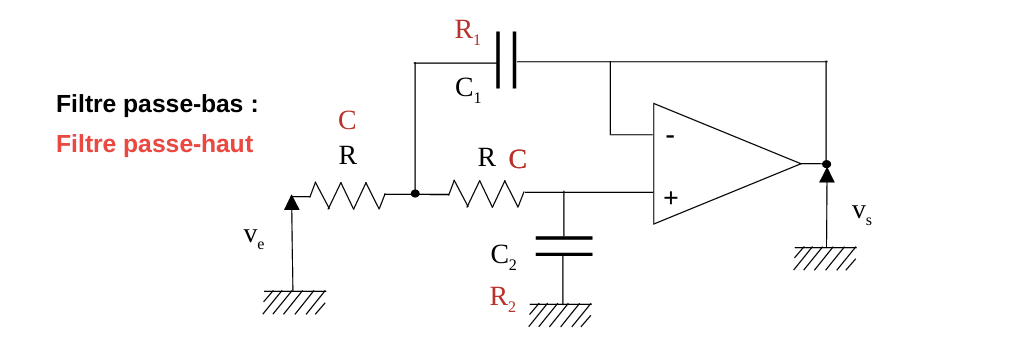
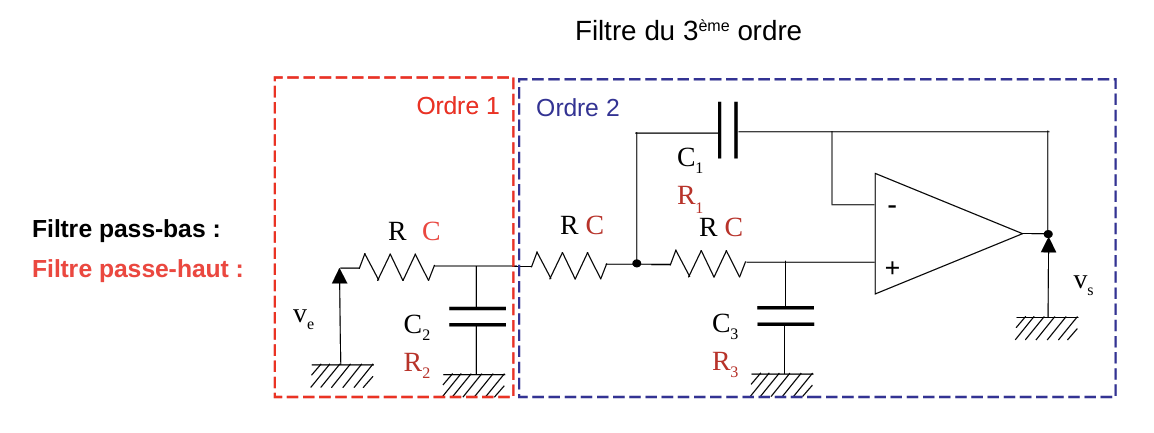
Passe-bas:
\[ C_{n, i}=\frac{K_{n, i}}{R \omega_0} \]
Passe-haut :
\[ R_{n, i}=\frac{1}{K_{n, i} C \omega_0} \]
Structure de Rauch
\[ H(p)=-\frac{R^2 C p}{C^2 R_1 R_2 p^2+C R_1 p+1+\frac{R_1}{R_3}} \quad \longrightarrow\left\{\begin{array}{l} \omega_0=\frac{\sqrt{1+\frac{R_1}{R_3}}}{C \sqrt{R_1 R_2}} \\ Q=\frac{1}{2} \sqrt{\frac{R_2}{R_1}\left(1+\frac{R_1}{R_3}\right)} \end{array}\right. \]






