Amplification 放大器
Amplification 放大器
概述
放大器
电子系统中,传感器或信号源输出电平非常微弱。为了满足后续电路(如滤波、模数转换、功率驱动等)的动态范围与信噪比要求,需在信号链中加入电压放大环节。
理想运算放大器在设计上追求以下性能指标:
- 开环电压增益无限大(\(\displaystyle A_0\to\infty\)),以保证微小输入差值也能被放大;
- 输入阻抗无限大(\(\displaystyle Z_\text{in}\to\infty\)),避免对信号源造成负载;
- 输出阻抗为零(\(\displaystyle Z_\text{out}\to0\)),确保对后级负载的电压传输;
- 带宽宽广,覆盖从直流到几十兆赫甚至更高频段。
在评价放大器性能时,通常关注以下几个指标:
- 增益 Gain
- 输入与输出阻抗 impédances d’entrée et de sortie
- 带宽 bande passante
- 噪声因子及噪声温度 facteur et la température de bruit
- 失真 distorsions
- 效率 rendement
- 动态范围 dynamique
放大器主要特性
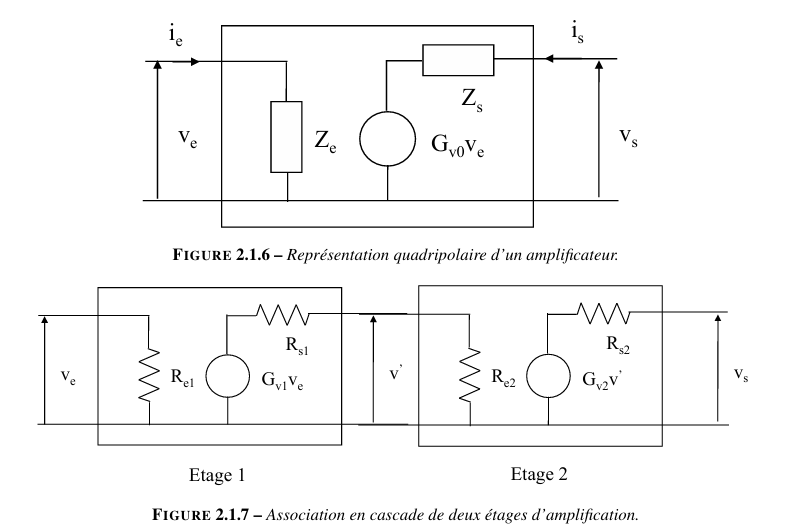
放大器在小信号线性工作情况下,可等效为图中所示的四端口网络。有:
- 电压增益 gain en tension \(G = V_s/V_e\)
- 输入阻抗 impédance d’entrée \(Z_e = V_e/i_e|_{i_s = 0}\)
- 输出阻抗 impédance de sortie \(Z_s = V_s/i_s|_{V_e= 0}\)
理想放大器特征:
- 输入阻抗无限大,避免对前级信号源造成负载;
- 输出阻抗为零,使输出电压不受负载影响;
- 增益在整个工作频带内保持常数。
实际放大器则具有有限的输入和输出阻抗,增益随频率变化。 增益随频率变化,增益带宽积保持不变。
放大器在级联放大模式下:
等效输入阻抗 impédance d'entrée \(R_{e,eq} = R_{e1}\)
等效输出阻抗 impédance de sortie \(R_{s,eq} = R_{s2}\)
空载总增益 gain de tension à vide \(G_{eq} = G_1 \cdot G_2 \cdot Att_{12}\)
其中,电压分配因子 Atténuation \(Att_{12} = \frac{R_{s1}}{R_{s1} + R_{e2}}\),\(R_{s1}\)为第一级输出阻抗,\(R_{e2}\)为第二级输入阻抗。
放大器的增益包括电压增益 \(G_v\)、电流增益 \(G_i\) 和功率增益 \(G_p\)。 - 电压增益 \(G_v = \frac{V_s}{V_e}\),单位为 V/V 或 dB - 电流增益 \(G_i = \frac{i_s}{i_e}\),单位为 A/A 或 dB - 功率增益 \(G_p = \frac{P_s}{P_e}\),单位为 W/W 或 dB
放大器的带宽(Bande passante)是因为实际放大器电压增益随频率变化而引起的。带宽是指增益大于某一特定值的频率范围。通常取增益下降到最大值的 -3dB 点时的频率范围。

从低频截止频率 \(f_{L}\) 到高频截止频率 \(f_{H}\),带宽为: \[ B = f_H - f_L \]
带宽的单位为赫兹(Hz),也可以用千赫兹(kHz)或兆赫(MHz)表示。
放大器的噪音因子和噪音温度(Facteur de bruit, Température de bruit)是用来描述放大器在工作时产生的噪音水平。噪音因子是指放大器输出端的信号噪声功率与输入端的信号噪声功率之比。噪音温度是指放大器在工作时产生的噪音等效于一个特定温度下的热噪声。
热噪音功率(Puissance de bruit thermique) \(P_n = k_B \cdot T \cdot B\),其中 \(k_B\) 为玻尔兹曼常数,\(T\) 为绝对温度,\(B\) 为带宽。
热噪音电压方差(Variance de bruit thermique) \(<v_{bruit}>^2 = 4 \cdot k_B \cdot T \cdot R_e\),其中 \(R_e\) 为输入阻抗。
噪音因子(Facteur de bruit) \(F = \frac{(SNR)_{in}}{(SNR)_{out}}\), 其中 \(SNR\) 为信噪比。
噪音温度(Température de bruit) \(T_n = \frac{F - 1}{F} \cdot T_0\),其中 \(T_0\) 为参考温度。
当多级放大器级联时,整体噪音因子可以有Friis公式计算: \[ \begin{aligned} &F_{\text {total }}=F_1+\frac{F_2-1}{G_1}+\frac{F_3-1}{G_1 G_2}+\ldots+\frac{F_n-1}{G_1 G_2 \ldots G_{n-1}}\\ &\text { or }\\ &T_{\text {total }}=T_1+\frac{T_2}{G_1}+\frac{T_3}{G_1 G_2}+\ldots+\frac{T_n}{G_1 G_2 \ldots G_{n-1}} \end{aligned} \]
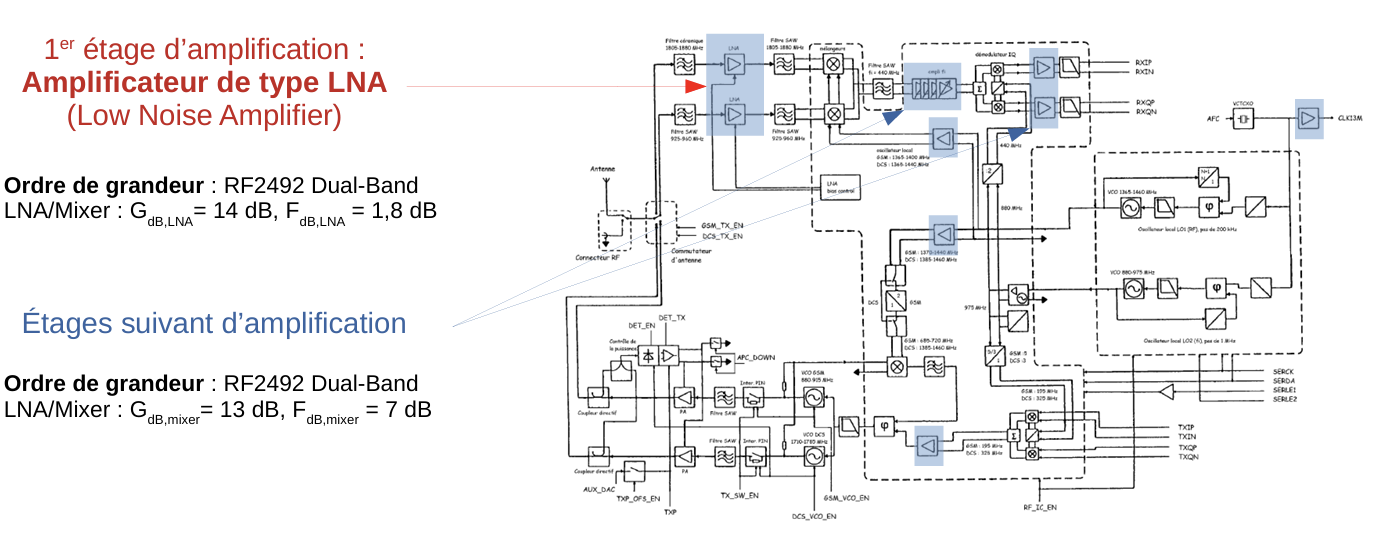
在射频前端,首级往往采用低噪声放大器(LNA)以提高系统灵敏度。
由于LNA的增益通常较大,因此后续级的噪声因子对系统整体噪声影响较小。即\(F_{\text {total }} \approx F_{\text {LNA }} .\)
低噪声放大器主要用于弱信号采集(如传感器读出、射频接收前端),其噪声因子和等效噪声温度是关键指标.
放大器的效率(Rendement)是指放大器输出功率与输入功率之比。效率通常用百分比表示。
- 效率(η) = \(\frac{P_{s}}{P_{f}}=\frac{P_{s}}{P_{s}+P_{d}}\),其中 \(P_{f}\) 为输入功率,\(P_{d}\) 为功耗。
放大器的失真(Distorsion)是指放大器输出信号与输入信号之间的差异。失真通常用百分比表示。
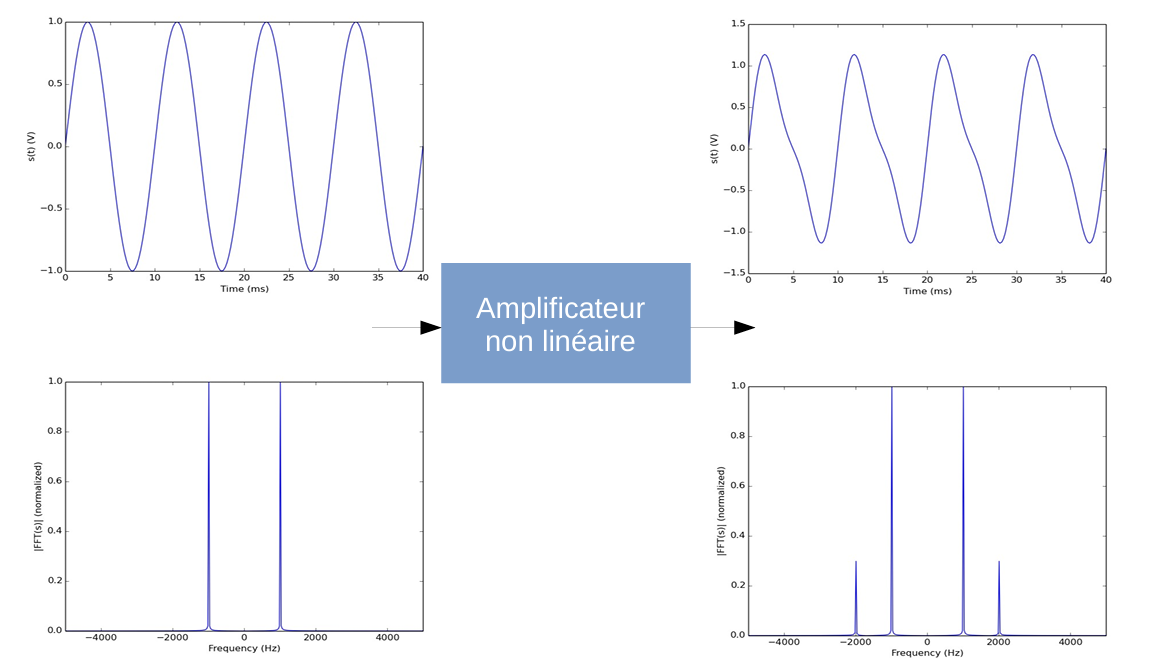
如上图,输入为正弦波,输出为失真波形。考虑信号的傅里叶级数展开:
\[ s(t)=a_0+\sum_{n=1}^{+\infty} a_n \cos \left(n \omega_0 t\right)+\sum_{n=1}^{+\infty} b_n \sin \left(n \omega_0 t\right) \] 其中,\(a_n\) 和 \(b_n\) 为傅里叶系数: \[ \begin{aligned} &a_n=\frac{1}{T} \int_0^T s(t) \cos \left(n \omega_0 t\right) d t \\& b_n=\frac{1}{T} \int_0^T s(t) \sin \left(n \omega_0 t\right) d t \\& a_0=\frac{1}{T} \int_0^T s(t) d t \end{aligned} \]
失真率(Taux de distorsion)可以表示为:
\[ d=\frac{\sqrt{A_2^2+A_3^2+\ldots+A_n^2}}{A_1} \quad A_n=\frac{a_n}{\sqrt{2}} \quad B_n=\frac{b_n}{\sqrt{2}} \]
即,失真率与高次谐波幅值成正比。
从另一个角度,考虑泰勒级数展开: \[ v_s=f\left(\Delta v_e\right)=f\left(v_{e 0}\right)+\Delta v_e \frac{f^{\prime}\left(v_{e 0}\right)}{1!}+\left(\Delta v_e\right)^2 \frac{f^{\prime \prime}\left(v_{e 0}\right)}{2!}+\left(\Delta v_e\right)^3 \frac{f^{\prime \prime \prime}\left(v_{e 0}\right)}{3!}+\ldots \]
其中一次项负责期望放大,二次、三次及更高次项引入谐波与互调产物,这导致了非线性失真。
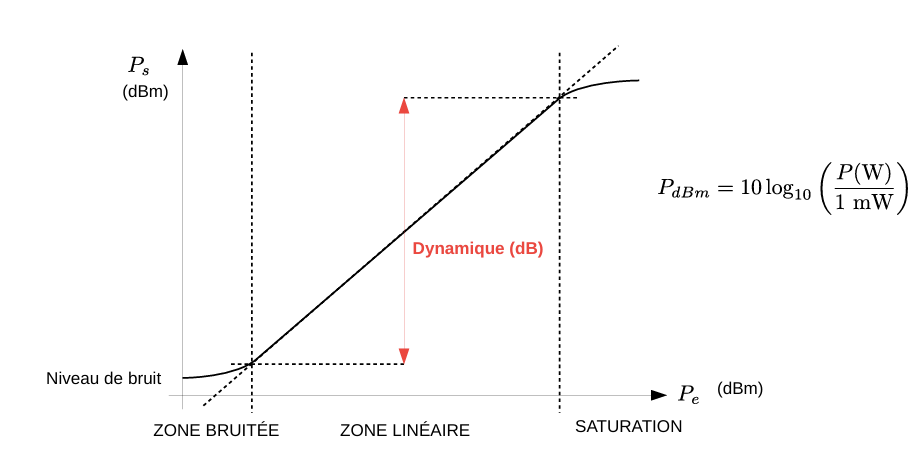
以输入功率为横坐标,输出功率为纵坐标,可以将功率曲线分为三个区域:
噪声区 (Zone Bruitée):输入极低时,输出被噪声底淹没;
线性区 (Zone Linéaire):输出与输入成正比,曲线斜率约为 1;
饱和区 (Saruration):放大器输出不再随输入线性增大。
其中,动态范围(Dynamique)定义为线性区顶部与噪声底功率之比。动态范围通常用分贝表示。
\[ \text { Dynamique }=P_{s, \max }-P_{\text {bruit }}(\mathrm{dB}) \]
运算放大器 Operational Amplifier, Op-Amp
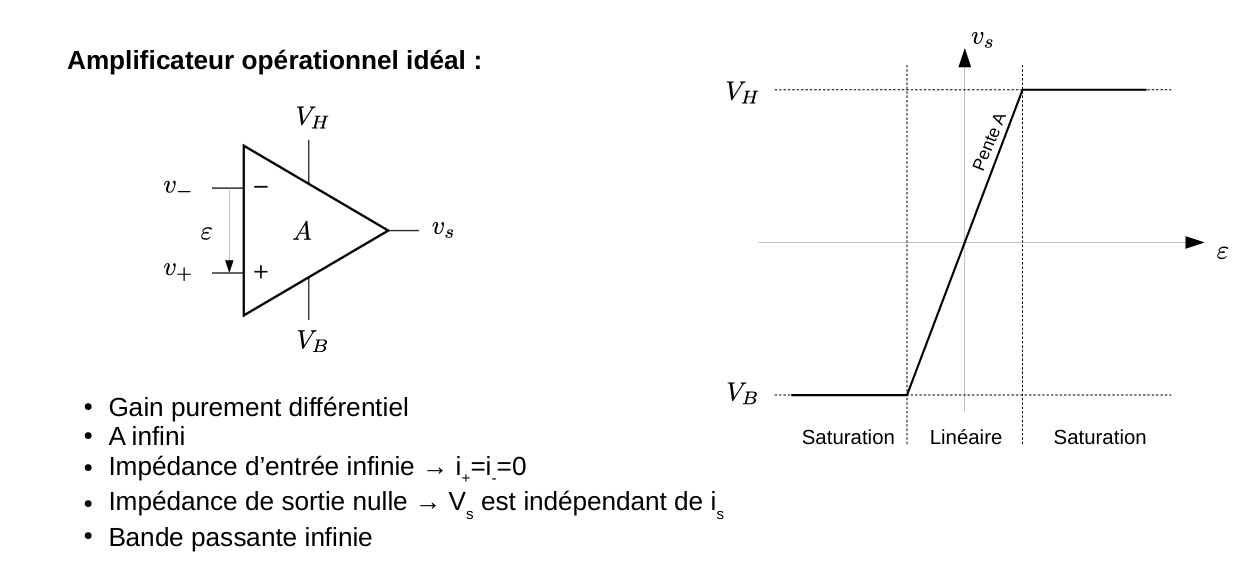
运算放大器(Operational Amplifier)是一种高增益差分放大器,设计之初用于模拟算术运算和精密信号处理。运算放大器具有高输入阻抗、低输出阻抗和宽带宽等特点,广泛应用于模拟信号处理、滤波、放大、比较等领域。
运算放大器的基本结构包括输入级、增益级和输出级。具有以下参数: - 电源电压 (Supply Voltages): \(V_H\), \(V_B\) —— 运算放大器两端的正负电源,可对称或不对称。
反相输入端 (Inverting Input): \(v^-\)
同相输入端 (Non‑inverting Input): \(v^+\)
输入差分电压 (Differential Input Voltage): \(\varepsilon = v^+ - v^-\)
开环增益 (Open‑loop Gain): \(A\)
输出电压 (Output Voltage): \(v_s = A \cdot \varepsilon\)(未考虑饱和时)。
理想运算放大器
理想运算放大器是一个理论模型,具有以下特性: - 纯差动放大 (Pure Differential Amplification):仅对两输入端差分电压放大,公共模式信号不放大。
开环增益无穷大 (Open-loop Gain \(A \to \infty\)):确保微小输入差分电压也能被放大。
输入阻抗无穷大 (Input Impedance \(\to \infty\)):输入电流 \(i^+ = i^- = 0\),避免对信号源造成负载。
输出阻抗为零 (Output Impedance \(\to 0\)):输出电压 \(v_s\) 不受负载电流 \(i_s\) 影响。
带宽无限 (Infinite Bandwidth):所有频率成分均可无衰减放大。
在理想模型下,输出 \(v_s\) 与差分电压 \(\varepsilon\) 之间呈线性关系,此区域称为线性区(Linear Region): \[ v_s = A \cdot \varepsilon \] 但当 \(A \cdot \varepsilon\) 超过电源限幅时,进入饱和区(Saturation)。
理想的运算放大器与实际运算放大器相比有以下差异: | 性质 | 理想模型 | 实际器件 | |-------------------------|---------------------------|--------------------------------| | 输入电阻 (Input Resistance) | \(R_e = +\infty\) | \(R_e > 10 \, R_i\) | | 输出电阻 (Output Resistance) | \(R_s = 0\) | \(R_s < \frac{R_L}{10}\) |
为了使得实际运算放大器接近理想模型,通常需要满足\(R_e \gg R_i, R_s \ll R_L\),以保证对前级信号源影响极小,同时能向后级负载提供足够电流而不致压降过大。
负反馈
在实际运算放大器应用中,存在两个主要问题: 1. 开环增益 \(A \gg 1\):即便极小的输入差分电压也会导致放大器输出饱和(Saturation),无法工作在线性区(Linear Region)。
- 不同器件间 \(A\) 大幅波动:电路性能对器件批次或温度漂移敏感。
为此,采用负反馈(Negative Feedback),将输出信号的一部分反馈到输入端,并从输入端减去,使得差分电压的维持在接近零的微小值,以保证放大器工作在线性区,并降低增益对器件参数的敏感性。
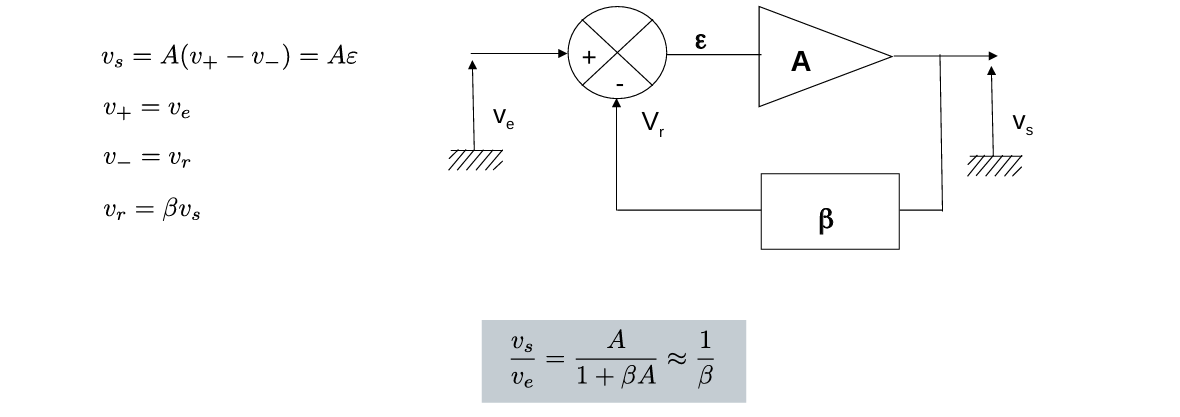
具体来说,引入负反馈系统之后,输入电压分别为\(v_+ = v_e, v_- = v_r = \beta v_s\);输出电压为\(V_s = A \cdot \varepsilon = A \cdot (V^+ - V^-)\)。
由此,负反馈使得闭环增益不再依赖于开环增益 \(A\),而是由反馈系数 \(\beta\) 决定: \[ \frac{v_s}{v_e}=\frac{A}{1+\beta A} \approx \frac{1}{\beta} \]
于此同时,引入负反馈将改善输入阻抗和输出阻抗: \[ Z_e^{\prime}=(1+\beta A) Z_e>Z_e, \quad Z_s^{\prime}=\frac{Z_s}{1+\beta A}<Z_s . \]
输入阻抗(Input Impedance):\(Z_e^{\prime} = (1 + \beta A) Z_e\),输入阻抗被放大 \((1 + \beta A)\) 倍,从而减少对前级信号源的负载影响。
输出阻抗(Output Impedance):\(Z_s^{\prime} = \frac{Z_s}{1 + \beta A}\),输出阻抗被缩小相同倍数,提高了驱动能力,减小了输出电压随负载变化的波动。
综上,负反馈稳定增益,优化阻抗,使得放大器性能更加接近理想模型。
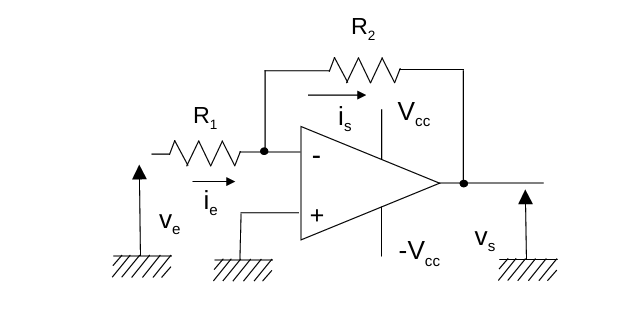
使用负反馈时,反向连接运算放大器,因此被称为反相放大器(Inverting Amplifier)。
- 输入电阻 \(R_1\)(Input Resistor)连接至反相输入端 \(v^-\)
- 反馈电阻 \(R_2\)(Feedback Resistor)从输出 \(v_s\) 接回到反相输入端
- 同相输入端 \(v^+\) 接地(地参考,\(0 \, \text{V}\))。
存在理想假设:
虚断(virtual open)由于输入阻抗趋于无穷大,输入电流几乎为零,即 \(i^+ = i^- = 0\),因此所有输入电流均流经反馈网络。
虚短(Virtual Short):由于开环增益 \(A \to \infty\),保持两输入端电压相等,即 \(v^- = v^+ = 0 \, \text{V}\)。
增益-带宽积 Gain-Bandwidth Product
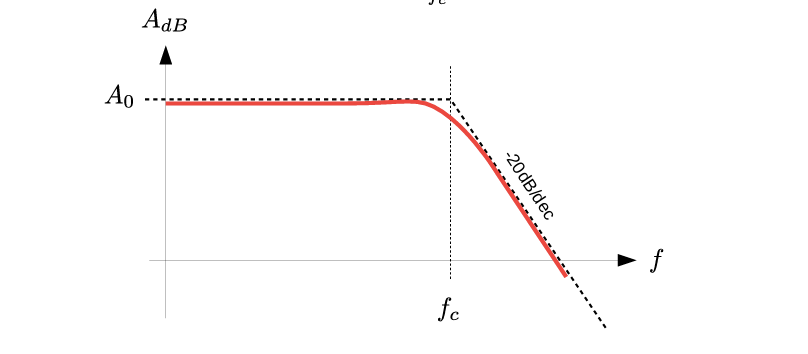
运算放大器内部往往集成有补偿电容(Compensation Capacitor),使其开环增益随频率表现为一阶低通滤波器特性。
\[ A(f)=\frac{A_0}{1+\frac{f}{f_c}} \] 其中,\(A_0\) 为直流增益(DC Open‑Loop Gain),\(f_c\) 为截止频率(Cut‑off Frequency)。
在负反馈模式下,有:
\[ \frac{v_s}{v_e}=\frac{A}{1+\beta A}=\frac{A_0^{\prime}}{1+j \frac{f}{f_c^{\prime}}} \]
故有,\(f\to 0\)时 $$
A_0^{}= , f_c^{}=f_c(1+A_0) $$
因此有,增益和带宽的乘积应使用为常数:
$$
A_0^{} f_c^{}=A_0 f_c $$
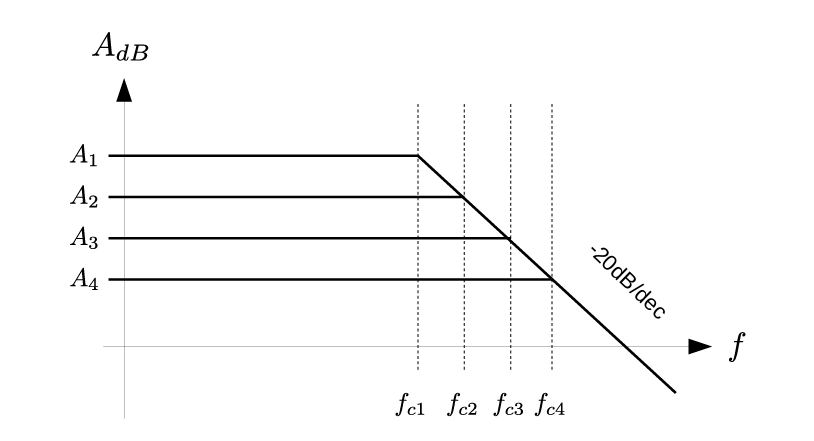
该常数决定了运放在不同闭环增益下的最大带宽。
传递函数 fonction de transfert

根据Millman 定理,对于任意节点电压,有:
\[ V=\frac{\sum_{i=1}^N \frac{V_i}{Z_i}}{\sum_{i=1}^N \frac{1}{Z_i}} \] 其中,\(V_i\) 为各个支路电压,\(Z_i\) 为各个阻抗。
考虑以下电路: 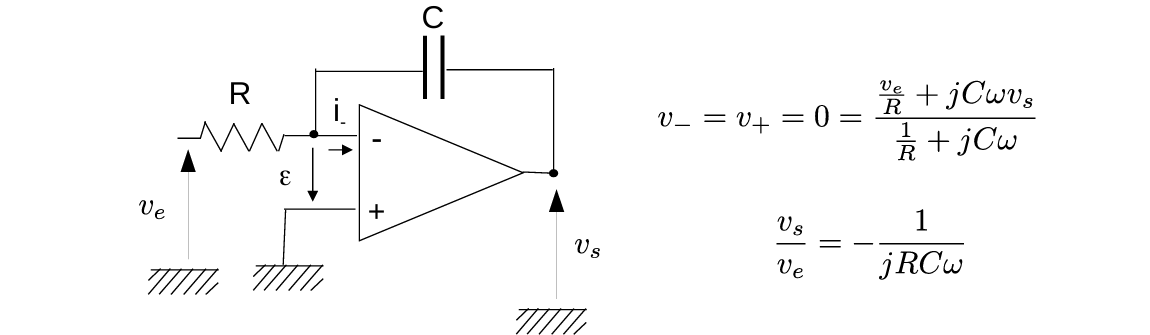
根据Millman 定理,在图中标出的点上有: \[ v_{-}=v_{+}=0=\frac{\frac{v_e}{R}+j C \omega v_s}{\frac{1}{R}+j C \omega} \] 因此可得, \[ \frac{v_s}{v_e}=-\frac{1}{j R C \omega} \] 即为该电路的运算放大器传递函数。
基于导纳(Admittance)的方法
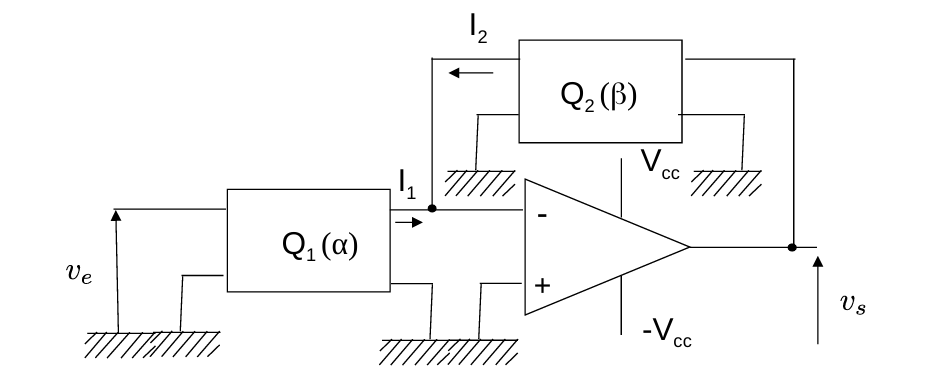
引入两个导纳块,电路可以如上表示。此时,标示点两端的电流和电压存在关系: \[ \begin{aligned} & i_1=\alpha(p) v_e(p) \\ & i_2=\beta(p) v_s(p) \end{aligned} \] 因此,此时的传递函数为: \[ A_v=-\frac{\alpha(p)}{\beta(p)} \] 其中,\(\alpha(p)\) 和 \(\beta(p)\) 分别为输入和输出导纳。
对于不同模块,其导纳如图所示: 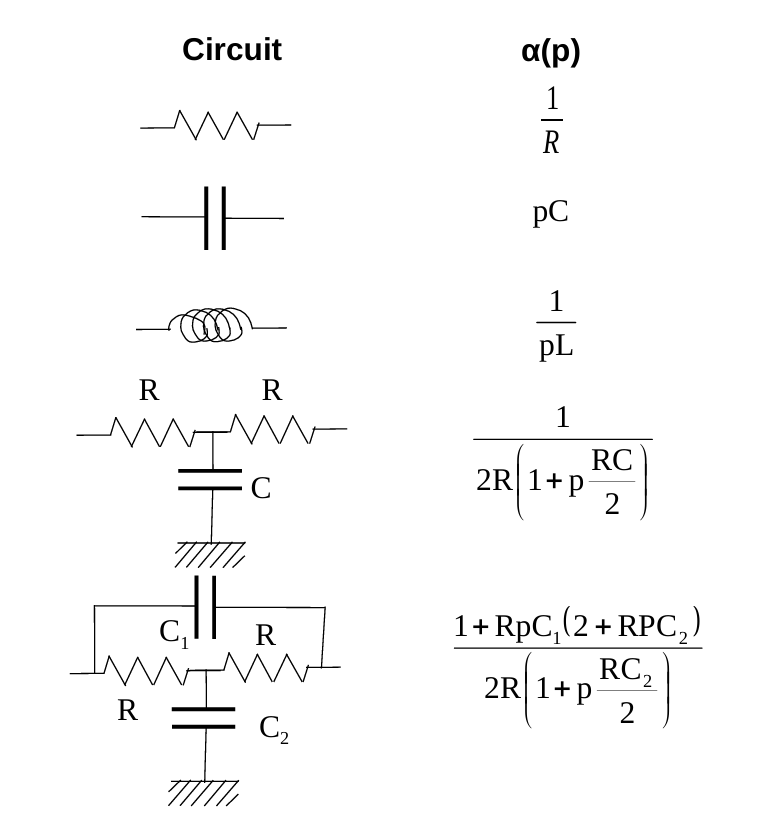
示例1:反向放大器 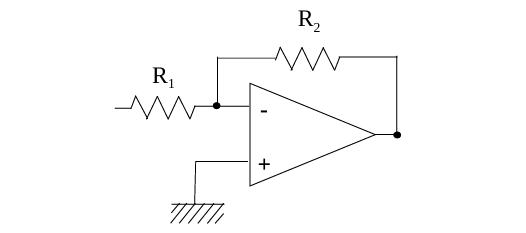
此时系统增益为\(R2/R1\)。
示例2:积分器(Integrator) 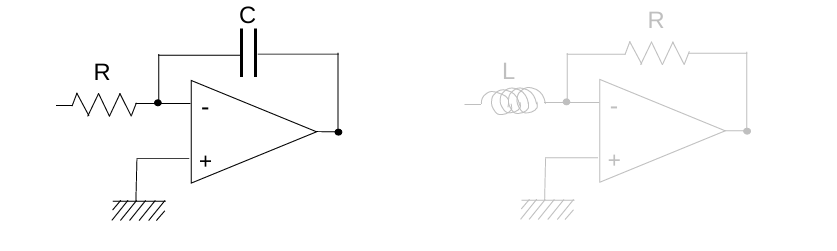 此时系统增益为\(-\frac{pC}{R}\)或\(pLR\)。
此时系统增益为\(-\frac{pC}{R}\)或\(pLR\)。
功率放大器 amplificateur de puissance
信号放大原理
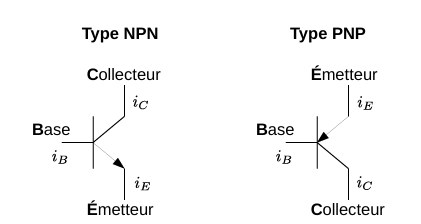 当输入的小信号在基极(base)施加电流\(i_B\)时,晶体管导通程度随之变化,从而控制来自电源的较大电流
\(i_C\)或 \(i_E\)(流经集电极(collector)或流向发射极(emitter))。这一过程使得输出端的功率\(P_out\)大大超过输入信号自身所携带的功率,实现功率放大(power
amplification)。
当输入的小信号在基极(base)施加电流\(i_B\)时,晶体管导通程度随之变化,从而控制来自电源的较大电流
\(i_C\)或 \(i_E\)(流经集电极(collector)或流向发射极(emitter))。这一过程使得输出端的功率\(P_out\)大大超过输入信号自身所携带的功率,实现功率放大(power
amplification)。
双极型晶体管 (Bipolar Transistor)可以分为NPN型和PNP型,如上图所示。
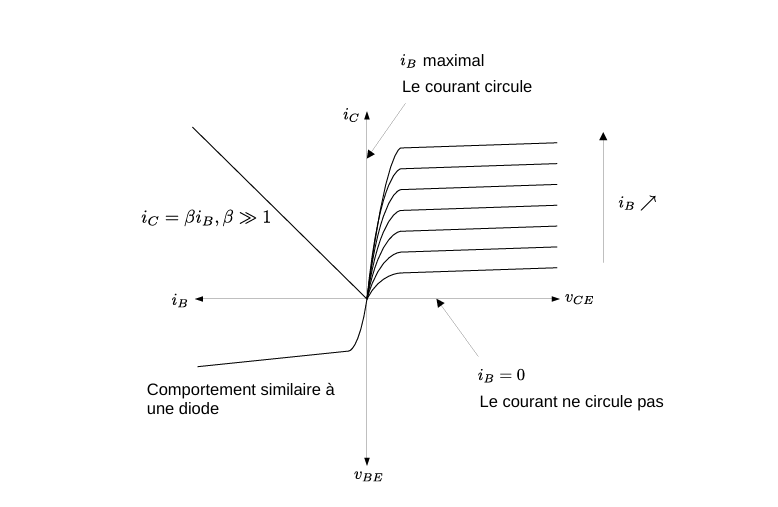
一般来说,输出电流与输出电流成正比关系: \[ i_C = \beta \cdot i_B \]
其中,\(\beta\)为电流增益(Current Gain),通常在100到1000之间。
功率放大器的工作类别
A类放大器 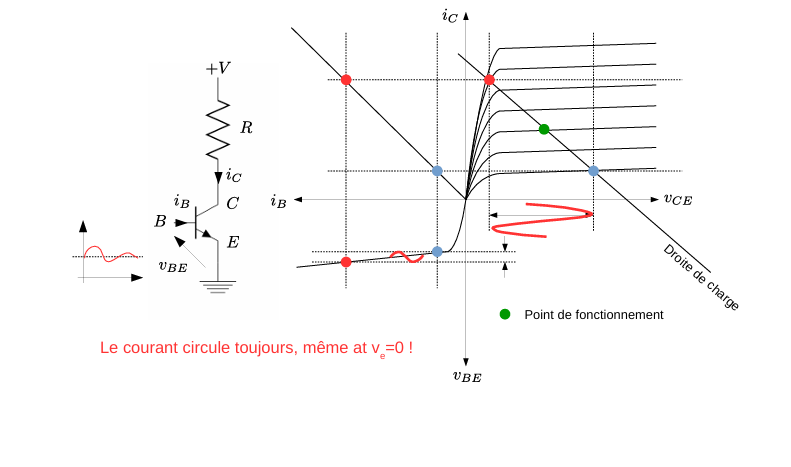
A 类放大器通过将晶体管持续偏置在导通区域,输入信号的正半周和负半周都能被放大。由于输出晶体管始终处于导通状态,因此功率损耗较大,效率较低。
负载线(Load Line):由 \(+V\) 与 \(R\) 决定的斜直线,用以限定集电极–发射极电压 \(v_{CE}\) 与电流 \(i_C\) 的关系。
偏置点(Bias Point):选择在特性曲线中点(绿色标记),确保输入信号正负半周均在放大区(active region)内变化,避免交越失真。
放大区(Active Region):在此区间,\(i_C \approx \beta \, i_B, \, \beta \gg 1\),基极微小电流 \(i_B\) 控制集电极电流 \(i_C\) 的大幅摆动。
饱和区与截止区:
- 截止区(Cutoff):当 \(v_{BE}\) 低于 PN 结导通电压(≈0.7 V)时,晶体管切断,只有静态电流。
- 饱和区(Saturation):当 \(v_{CE}\) 过低,晶体管完全导通,输出受限于外部负载。
优点:线性度高,失真小,全波放大,适合高保真音频放大。
缺点:效率低,发热量大,功耗高。
B类放大器
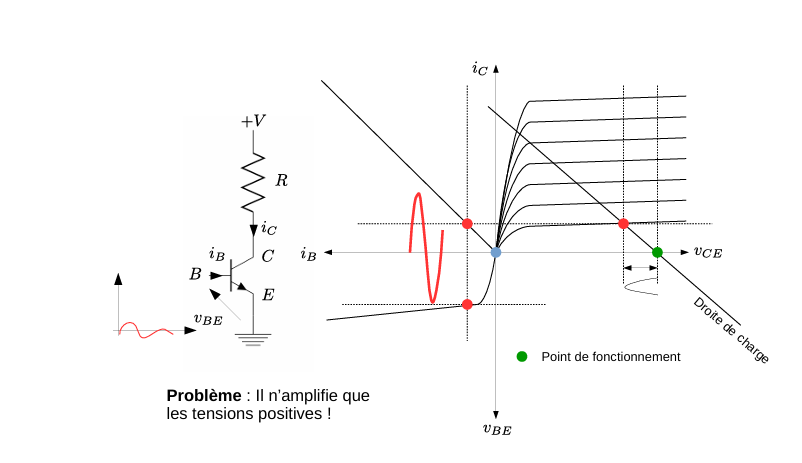
Class B 放大器中,晶体管(transistor)的基极–发射极电压 \(v_{BE}\)被偏置到截止点(cutoff point),即静态时无电流流过。仅当输入信号使\(v_{BE}\)过约 0.7 V(PN 结导通阈值)时,晶体管才导通(conduction),对输入信号的**正半周(positive half‑cycle)进行放大
负载线 (Load Line):由电源电压 \(+V\) 和负载电阻 \(R\) 决定,图中以斜直线表示。
截止区 (Cutoff Region):对应基极电流 \(i_B = 0\),集电极电流 \(i_C \approx 0\)(图中蓝色点)。
放大区 (Active Region):当 \(v_{BE}\) 超过阈值时,沿负载线与不同 \(i_B\) 值的 I–V 曲线交点移动,形成输出电流脉动(图中绿色点为信号最大正峰工作点)。
输入–输出映射:红色波形示意基极电压变化,只有上半部在集电极产生对应电流。
优点
- 效率高:在单端单管工作模式下,理论最高效率可达 \(𝜂≈78\%\),适合中等功率应用。
- 结构简单:单管即可放大半周信号。
缺点
- 半波放大:单管只能放大正半周信号,若需全波输出,需采用推挽式结构,至少两只晶体管分别放大正负半周信号。
- 交越失真:正负半周切换处的信号重构会产生失真,影响线性度。
- 附加电路需求:需要偏置电路和信号复位网络以减小失真,增加了电路复杂度。
C类放大器 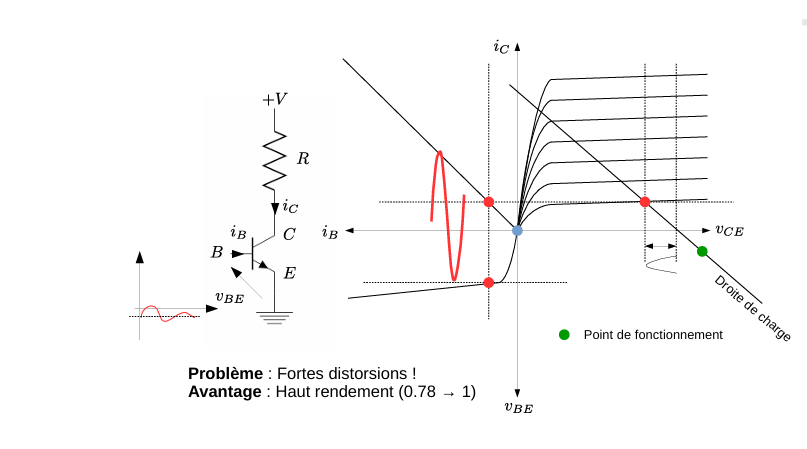
限幅放大 (Pulse Amplification):Class C 放大器的输入信号仅在正峰超过阈值时触发,输出为窄脉冲。这种工作模式直接驱动负载会产生严重失真(distortion),无法满足高保真信号放大的需求。
谐振负载 (Resonant Load):实际应用中,Class C 放大器常配合谐振电路(resonant circuit)或调谐电路(tuned circuit)使用。谐振器(tank circuit)由电感和电容组成,能够滤除高次谐波,仅保留基频成分,从而在输出端恢复正弦波形。
优点:效率高,适合高频信号放大,如射频功率放大器。
缺点:失真严重,需要谐振负载;导通角小,需精确谐振调谐 (tuning) 增加设计复杂度
Class C 放大器因其高效率和低功耗,广泛应用于无线通信中的射频功率放大器和发射机中。






