从小波到压缩
从小波到压缩
PLAN
- 小波的实际应用
- 压缩特性
- 如何选择小波
小波的实际应用
前置内容的小结
多分辨率分析
定义为一系列嵌套的希尔伯特子空间 \(\{V_j\}_{j \in \mathbb{Z}}\),描述了尺度 \(2^j\) 上的函数行为,配备一个函数 \(\theta\),它在 \(V_0\) 上生成一个 Riesz 基。
由 \(\theta\) 推导出一个尺度函数 \(\phi\),满足如下性质:
对于每个 \(j \in \mathbb{Z}\),
\[ \left\{ \frac{1}{\sqrt{2^j}} \phi \left( \cdot - \frac{2^j n}{2^j} \right) \right\}_{n \in \mathbb{Z}} \]
是 \(V_j\) 的希尔伯特基。
共轭镜像滤波器
\(h = (h_n)_{n \in \mathbb{Z}}\) (低通滤波器)和 \(g = (g_n)_{n \in \mathbb{Z}}\) (高通滤波器),满足以下条件:
\[ \begin{cases} h_n = \left(\frac{1}{\sqrt{2}} \phi(\cdot / 2), \phi(\cdot-n)\right), \\ \widehat{\phi}(2\omega) = \widehat{\phi}(\omega) \frac{\widehat{h}(\omega)}{\sqrt{2}}, & \omega \in \mathbb{R}, \end{cases} \]
并且
\[ \begin{cases} g_n = (-1)^{1-n} h_{1-n}, \\ \widehat{g}(\omega) = e^{-i\omega} \widehat{h}(\omega + \pi), \end{cases} \]
小波函数
选定小波函数 \(\psi\)以满足:
\[ \begin{cases} g_n = \left(\frac{1}{\sqrt{2}} \psi(\cdot / 2), \phi(\cdot - n)\right), \\ \widehat{\psi}(2\omega) = \widehat{\phi}(\omega) \frac{\widehat{g}(\omega)}{\sqrt{2}}, \end{cases} \]
从而使
\[ \left\{ \frac{1}{2^j} \psi \left( \cdot - \frac{2^j n}{2^j} \right) \right\}{n \in \mathbb{Z}} \]
是 \(W_j\) 的希尔伯特基(其中 \(V_j \oplus W_j = V_{j-1}\))。
由于 \(V_j = V_{j+1} \oplus W_{j+1}\),我们可以写为: 对于 \(L < J\),
\[ V_L = V_J \oplus W_J \oplus W_{J-1} \oplus \cdots \oplus W_{L+2} \oplus W_{L+1}, \]
因此对于任何 \(L^2\) 中的函数,
\[ P_{V_L} f = P_{V_J} f + \sum_{j=L+1}^{J} P_{W_j} f. \]
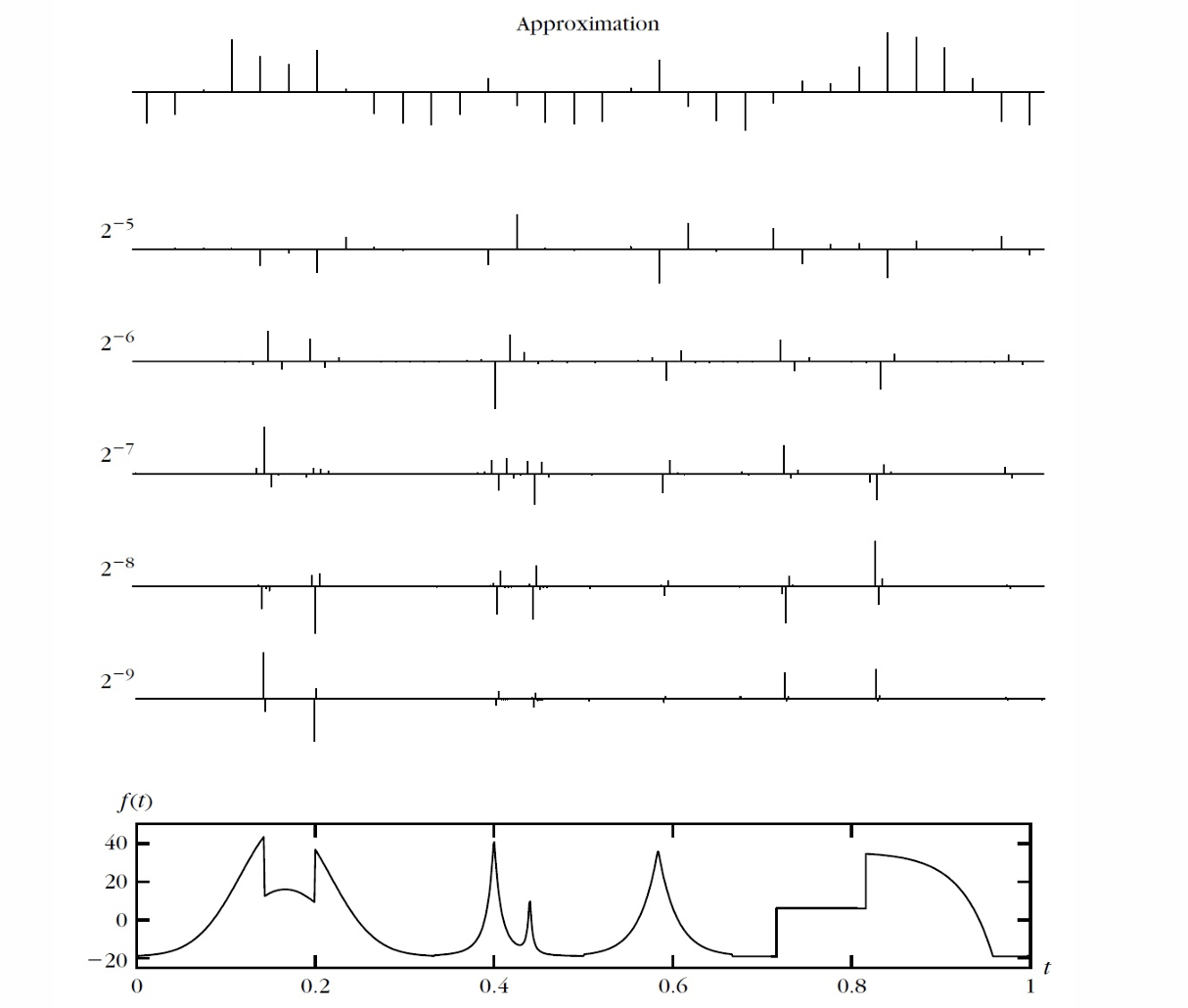
快速小波变换算法 Fast wavelet transform algorithm
假设我们知道\(P_{V_0} f\),即假设:
\[ P_{V_0} f = \sum_{-\infty}^{\infty}a_{0,n} \phi_{0, n}= \sum_{-\infty}^{\infty}\left(f, \phi_{0, n}\right) \phi_{0, n} \]
根据之前的假设:\(P_{V_j}f = P_{V_{j+1}}f + P_{W_{j+1}}f\),可以计算对应\(P_{V_1} f\) 和 \(P_{W_1} f\) 的内积 \((a_{1,p})_{p \in \mathbb{Z}}\) **和 \((d_{1,p})_{p \in \mathbb{Z}}\):
\[ P_{V_0} f = \sum_p a_{1,p} \phi_{1,p} + \sum_p d_{1,p} \psi_{1,p} \]
递归分解 Recursive decomposition
根据上式计算 \((a_{1,p})_{p \in \mathbb{Z}}\) **和 \((d_{1,p})_{p \in \mathbb{Z}}\):
\[ \begin{aligned} a_{1, p} & =\left(\phi_{1, p}, P_{V_0} f\right) =\sum_n a_{0, n}\left(\phi_{1, p}, \phi_{0, n}\right) =\sum_n a_{0, n}\left(\phi_{1,0}, \phi_{0, n-2 p}\right) \\ & =\sum_n a_{0, n} h_{n-2 p} =\left(a_0 \star \bar{h}\right)_{2 p} \end{aligned} \]
\[ \begin{aligned}d_{1, p} & =\left(\psi_{1, p}, P_{V_0} f\right) =\sum_n a_{0, n}\left(\psi_{1, p}, \phi_{0, n}\right) =\sum_n a_{0, n}\left(\psi_{1,0}, \phi_{0, n-2 p}\right) \\& =\sum_n a_{0, n} g_{n-2 p} =\left(a_0 \star \bar{g}\right)_{2 p}\end{aligned} \]

因此,无需知道 \(\psi\) 和 \(\phi\) 的复杂表达式即可完成分解。
初始化
从定义在区间 \([0,1]\) 上的函数 \(f \colon [0,1] \to \mathbb{R}\) 开始,假设其在 \(N = 2^{-L}\) 个点上均匀采样(采样间隔为 \(T = 2^L\))。计算初始系数:
\[ a_{L,n} = \int f(t) \phi_{L,n}(t) \, dt = \int f(t) \frac{1}{\sqrt{N}} \phi \left( \frac{t - (N^{-1}n)}{N^{-1}} \right) \, dt \approx N^{-1/2} f(N^{-1}n). \]
快速逆变换
根据之前的公式:
\[ P_{V_0} f = \sum_p a_{1,p} \phi_{1,p} + \sum_p d_{1,p} \psi_{1,p} = \sum_p a_{0,p} \phi_{0,p}. \]
有:
\[ a_{0,p} = (\phi_{0,p}, P_{V_0} f) = \sum_n a_{1,n} (\phi_{0,p}, \phi_{1,n}) + \sum_n d_{1,n} (\phi_{0,p}, \psi_{1,n}). \]
使用特性展开:
\[ a_{0,p} = \sum_n a_{1,n} h_{p-2n} + \sum_n d_{1,n} g_{p-2n}. \]
表示为卷积和上采样:
\[ a_{0,p} = \left(a_1^{\uparrow} \star h\right)_p+\left(d_1^{\uparrow} \star g\right)_p \]
其中,上采样 \(u^\uparrow\) 满足 \(u^\uparrow_{2n} = u_n\) 且 \(u^\uparrow_{2n+1} = 0\)。

算法复杂度
- 假设滤波器 \(h\) 和 \(g\) 的支持集大小为 \(K\)(即 \(K\) 个非零元素)。
- 假设 \(a_L\) 的支持集大小为 \(N\)。
- 因此,从尺度 \(2^L\) 到 \(2^{L-1}\) 的变换需要 \(2KN\) 次加法和乘法。
- 当 \(K\) 很小时,该算法比 FFT(快速傅里叶变换)更快。
处理定义域的边界
- 一个实际问题是,小波对不连续非常敏感 → 需要避免定义域边界的人工不连续性。
- 两种解决思路:
- 在区间 \([0, 2]\) 上采用对称性和“周期化 periodization”处理。
- 使用专门的边界小波。
图像小波
张量积的概念将一维扩展到二维
命题
设 \(V_1\) 和 \(V_2\) 是 \(L^2(\mathbb{R})\) 的两个希尔伯特子空间,其希尔伯特基为 \(\{e_n^i\}{n \in \mathbb{Z}}, \, i = 1, 2\)。 定义乘积空间:
\[ V = V_1 \otimes V_2 = \mathrm{clos}\{f : \mathbb{R} \times \mathbb{R} \to \mathbb{R}, \, f(x_1, x_2) = \sum_n \lambda_n f_n^1(x_1) f_n^2(x_2), \, f_n^1 \in V_1, \, f_n^2 \in V_2\}. \]
则集合
\[ \left\{e_{n_1}^1\left(x_1\right) \cdot e_{n_2}^2\left(x_2\right)\right\}_{\left(n_1, n_2\right) \in \mathbb{Z}^2} \]
是 \(V\) 的一个希尔伯特基。
当然,同样的原理可用于二维傅里叶变换:
\[ \begin{array}{ll} e^{\mathrm{i} 2 \pi n t} & \rightarrow 1 D \\ e^{\mathrm{i} 2 \pi\left(n_1 x_1+n_2 x_2\right)} & \rightarrow 2 D \end{array} \]
对于小波分析

对每个 \(j \in \mathbb{Z}\),定义
\[ V_j^2 = V_j \otimes V_j, \]
并定义空间 \(W_j^2\),使得
\[ V_{j-1}^2 = V_j^2 \oplus W_j^2. \]
定义三种类型的小波:
\[ \begin{cases} \psi^1(x_1, x_2) = \phi(x_1) \psi(x_2), \\ \psi^2(x_1, x_2) = \psi(x_1) \phi(x_2), \\ \psi^3(x_1, x_2) = \psi(x_1) \psi(x_2). \end{cases} \]
然后定义:
\[ \psi_{j, n_1, n_2}^k(x_1, x_2) = \frac{1}{2^j} \psi^k\left(\frac{x_1 - 2^j n_1}{2^j}, \frac{x_2 - 2^j n_2}{2^j}\right). \]
集合
\[ \{\psi_{j, n_1, n_2}^1, \psi_{j, n_1, n_2}^2, \psi_{j, n_1, n_2}^3\}_{(n_1, n_2) \in \mathbb{Z}^2} \]
是 \(W_j^2\) 的一个希尔伯特基。

压缩 Compression
全局和局部正则化
傅里叶变换的正则性与衰减
函数 \(f\) 的正则性 \(↔\) \(f\) 可微分的次数。
如果 \(\hat{f} \in L^1(\mathbb{R})\),则傅里叶反演公式表明:
\[ |f(t)| \leq \frac{1}{2\pi} \int_{-\infty}^\infty |e^{i\omega t} \hat{f}(\omega)| d\omega = \frac{1}{2\pi} \int_{-\infty}^\infty |\hat{f}(\omega)| d\omega < +\infty, \quad t \in \mathbb{R}. \]
此外,若 \(f\) 有界并且 \(p\) 次连续可微且导数有界,则需满足:
\[ \int_{-\infty}^\infty |\hat{f}(\omega)| (1 + |\omega|^p) d\omega < +\infty. \]
特别地,若存在 \(K > 0, \epsilon > 0\),使得:
\[ |\hat{f}(\omega)| \leq \frac{K}{1 + |\omega|^{p+1+\epsilon}}, \quad \forall \omega \in \mathbb{R}, \]
则 \(f \in C^p\)。
此外,还可以将可微性扩展到非整数阶。
Sobolev意义下的正则性
定义 1:
若函数 \(f \in L^2(\mathbb{R})\) 满足
\[ \int (1 + |\omega|)^2 |\hat{f}(\omega)|^2 d\omega < +\infty, \]
则 \(f\) 在 Sobolev 意义下可微。
定义 2:
令 \(s \in \mathbb{R}\)。若分布 \(u\) 在 \(\mathbb{R}^d\) 上满足以下条件,则称其属于 Sobolev 空间 \(H^s(\mathbb{R}^d)\):
- \(u \in S'\)(分布空间的对偶);
- \(\hat{u} \in L^1_{\text{loc}}(\mathbb{R}^d)\);
- \(u\) 满足正则性条件:
\[ \int (1 + |\omega|^2)^s |\hat{u}(\omega)|^2 d\omega < +\infty. \]
- 函数傅里叶变换的衰减是理解小波近似效率的重要概念。
- 然而,仅依赖全局正则性是不够精确的。
- \(\hat{f}\) 在无穷远处的衰减取决于 \(f\) 最严重的奇异性行为。
例如:
- \(f = \mathbb{1}_{[-1,1]}\) 在两个点不连续,因此 \(\hat{f}\) 的衰减为 \(\omega^{-1}\)。
- 然而,\(f\) 在两个奇异性点之外是正则的。
- 因此,我们需要引入局部正则性的概念。
Lipschitz 正则性
假设 \(f\) 在区间 \(]u-h, u+h[ \subset \mathbb{R}\) 中 \(m\) 次可微,其中 \(h > 0\)。
泰勒公式表明,\(f\) 可表示为:
\[ f(t) = p_u(t) + \epsilon_u(t), \quad t \in ]u-h, u+h[, \]
其中:
\[ p_u(t) = \sum_{k=0}^{m-1} \frac{f^{(k)}(u)}{k!} (t-u)^k, \]
并且
\[ |\epsilon_u(t)| \leq \frac{|t-u|^m}{m!} \sup_{v \in ]u-h, u+h[} |f^{(m)}(v)|. \]
因此,\(f\) 的 \(m\)-阶可微性为 \(\epsilon_u\) 提供了一个上界,这引出了 Lipschitz 正则性 的概念。
定义
令 \(\alpha \geq 0\)。
若存在一个多项式 \(p_u\)(次数 \(m < \alpha\))和一个常数 \(K > 0\),使得对任意 \(t \in \mathbb{R}\):
\[ |f(t) - p_u(t)| \leq K |t-u|^\alpha, \]
则称函数 \(f\) 在 \(u\) 处是 Lipschitz \(\alpha\)。
若存在 \(K > 0\),使得 \(f\) 在区间 \([a,b]\) 上每一点 \(u\) 都是 Lipschitz \(\alpha\),并且具有相同的 Lipschitz 常数 \(K\),则称 \(f\) 在 \([a,b]\) 上是统一的 Lipschitz \(\alpha\)。
- 一个在 \(u\) 处有界但不连续的函数是 Lipschitz 0。
- 如果 \(f\) 在 \(u\) 的邻域内是统一 Lipschitz \(\alpha > m\),则 \(f\) 在该邻域内 \(m\) 次连续可微。
小波的消失矩 Vanishing moments of a wavelet
对于一个小波 \(\psi\)、位置参数 \(u \in \mathbb{R}\) 和尺度因子 \(s > 0\),定义:
\[ \psi_{u,s} : t \mapsto \frac{1}{\sqrt{s}} \psi\left(\frac{t-u}{s}\right). \]
假设 \(f\) 在 \(u\) 处是 Lipschitz \(\alpha\),则 \(f = p_u + \epsilon_u\),其中 \(p_u\) 是一个次数 \(m < \alpha\) 的多项式。
是否可能满足以下性质?
\[ (f, \psi_{u,s}) = (p_u, \psi_{u,s}) + (\epsilon_u, \psi_{u,s}) = 0 + (\epsilon_u, \psi_{u,s}). \]
→ 换句话说,\(\psi_{u,s}\) 不“感知”多项式。
- 如果 \(f\) 足够正则并在局部表现得像多项式,则内积会非常小。
定义
若 \(\psi\) 满足
\[ \int t^k \psi(t) dt = 0, \quad \forall 0 \leq k < m, \]
则称 \(\psi\) 具有 \(m\) 阶消失矩。
这表明 \(\psi\) 与任意次数小于 \(m\) 的多项式正交:
若 \(p \in \mathbb{R}[X], \deg p < m\),则 \((\psi, p) = 0\)。
而且,正交性在尺度和平移下具有不变性:
\[ \int p(t) \frac{1}{\sqrt{s}} \psi\left(\frac{t-u}{s}\right) dt = 0, \quad \forall u \in \mathbb{R}, s > 0. \]
假设与结论
假设 \(\psi\) 具有 \(m\) 阶消失矩。
假设 \(f\) 在 \(v\) 处是 Lipschitz \(\alpha\),则存在次数 \(\deg p_v < \alpha\) 的多项式 \(p_v\),且有
\[ |f(t) - p_v(t)| \leq K |t-v|^\alpha. \]
当 \(\alpha \leq m\) 时,
\[ (p_v, \psi_{u,s}) = 0, \quad \forall u \in \mathbb{R}, s > 0. \]
因此:
\[ \begin{aligned}&\left|\left(f, \psi_{u, s}\right)\right|=\left|\int\left(f(t)-p_v(t)\right) \frac{1}{\sqrt{s}} \psi\left(\frac{t-u}{s}\right) \mathrm{d} t\right| \\& \leq \int K|t-v|^\alpha \frac{1}{\sqrt{s}}\left|\psi\left(\frac{t-u}{s}\right)\right| \mathrm{d} t \\& x=(t-u) / s \\& \leq \sqrt{s} \int K|s x+u-v|^\alpha|\psi(x)| \mathrm{d} x\end{aligned} \]
特别的,\(u = v\)时,有:
\[ \begin{aligned}\left|\left(f, \psi_{v, s}\right)\right| & \leq K s^{\alpha+1 / 2} \int|x|^\alpha|\psi(x)| \mathrm{d} x \\& \leq K^{\prime} s^{\alpha+1 / 2}\end{aligned} \]
当\(f\)的局部正则性增加,且小波具有消失矩时,内积衰减速度更快。
逼近率 Approximation rates
线性逼近 linear approximation
令 \(B = (e_n)_{n \in \mathbb{N}}\) 为一个可分希尔伯特空间的希尔伯特基。对于 \(f \in E\) 的线性逼近,定义为 \(f_N\),它是 \(f\) 在由 \(B\) 的前 \(N\) 个元素(通常无需失一般性)所张成的有限维空间上的正交投影:
\[ f_N = \sum_{n=0}^{N-1} (f, e_n)e_n. \]
逼近的误差为:
\[ \varepsilon_1(N) = \| f - f_N \|^2 = \sum_{n=N}^{+\infty} |(f, e_n)|^2. \]
非线性逼近 Non-linear approximation
对于 \(f \in E\) 的非线性逼近,定义为 \(f_N\),它是 \(f\) 在由 \(B\) 的 \(N\) 个向量 \(e_n\)(对应于最大的 \((f, e_n)\) 内积的索引 \(i_N = \{i_1, \dots, i_N\} \in \mathbb{N}^N\)所张成的有限维空间上的正交投影。
- 非线性逼近 \(\implies f_N + g_N \neq (f + g)_N\)
- 思路:自适应网格,在 \(f\) 的奇异性邻域更细化。
关于 \(L^2[0,1]\) 的一些理论结果
- 回忆信号处理课程中的知识:集合 \(\{t \mapsto e^{i 2\pi n t}\}_{n \in \mathbb{Z}}\) 是 \(L^2([0,1])\) 的一个希尔伯特基。
- 如果 \(f \in L^2([0,1])\),那么 \(f\) 可以写成一个傅里叶级数:
\[ f(t) = \sum_{k=-\infty}^{+\infty} (f, e^{i 2\pi k t}) e^{i 2\pi k t}, \]
- 其中:
\[ (f, e^{i 2\pi k t}) = \int_0^1 f(t) e^{-i 2\pi k t} \, dt. \]
- 定义 \(W^s([0,1])\) 为 \(L^2([0,1])\) 的子集,其元素在 Sobolev 意义上 \(s\) 次可微,且支持集在 \([0,1]\) 中。
\(f \in W^s([0,1])\) 当且仅当以下断言之一成立:
- \(\sum_{k \in \mathbb{Z}} |k|^{2s} |(f, e^{i2\pi kt})|^2 < \infty\)
- \(\sum_{N=1}^\infty N^{2s} \frac{\varepsilon_1(N)}{N} < \infty \implies \varepsilon_1(N) = o(N^{-2s})\)
- 线性逼近的误差:在线性逼近中,傅里叶基下的误差仅在 \(f\) 具有较高的 Sobolev 正则性 \(s\) 时快速衰减。
- 如果 \(f\) 在某处不连续,则 \(f \notin W^s([0,1])\),无论 \(s > 1/2\)。
- 因此 \(\varepsilon_1(N) = O(N^{-1})\)(缓慢衰减 + Gibbs 振荡)。
小波情形
在 \(V_L \cap W^s([0,1])\) 中,有 \(N = 2^{-L} + 1\) 个定义在 \([0,1]\) 上的尺度函数,因此:
\[ f_N = P_{V_L} f = \sum_{n=0}^{2^{-L}} (f, \phi_{L,n}) \phi_{L,n}. \]
逼近误差可写为:
\[ \varepsilon_1 = \|f - f_N\|^2 = \sum_{j=-\infty}^L \sum_{n=0}^{2^{-j}} |(f, \psi_{j,n})|^2. \]
假设小波 \(\psi\) 具有 \(m\) 个消失矩,\(0 < s < m\)。则函数 \(f \in W^s([0,1])\) 当且仅当:
\[ \sum_{N=1}^\infty N^{2s} \frac{\varepsilon_1(N)}{N} < \infty \implies \varepsilon_1(N) = o(N^{-2s}). \]
相较于傅里叶逼近没有收益
非线性逼近速率
假设小波函数具有 \(m\) 个消失矩。假设 \(f\) 在 \([0,1]\) 上有有限个间断点,并且在间断点之间的 \([0,1]\) 上是一致的 Lipschitz \(\alpha\)(其中 \(1/2 < \alpha < m\))。则线性逼近的误差上界为:
\[ \varepsilon_1(N) = O(N^{-1}). \]
然而,非线性上界:
\[ \varepsilon_{nl}(N) = O(N^{-2\alpha}). \]
选择小波
小波的构造
我们希望选择具有消失矩的 \(\psi\)。
我们希望:
\[ \begin{aligned}\int t^k \psi(t) \mathrm{d} t & =0, & 0 \leq k<m \\\Longrightarrow \quad \widehat{\psi}^{(k)}(0) & =0, & 0 \leq k<m\end{aligned} \]
- 因为 \(\hat{\psi}^{(k)}(0) = \int (-it)^k \psi(t) dt\)。
因此,当 \(|\hat{\psi}(\omega)| \underset{\omega \to 0}{=} O(\omega^m)\) 时,\(\psi\) 具有 \(m\) 个消失矩。
(由于 \(\hat{\psi}(\omega) \underset{\omega \to 0}{=} \hat{\psi}(0) + \omega \hat{\psi}^{(1)}(0) + \frac{\omega^2}{2!} \hat{\psi}^{(2)}(0) + \cdots\))
回忆以下公式:
\[ \hat{\psi}(\omega) = \frac{\hat{g}(\omega)}{\sqrt{2}} \hat{\phi}(\omega/2) \]
- 且 \(\hat{\phi}(\omega/2) \underset{\omega \to 0}{=} O(1)\)。
因此:
\[ |\hat{g}(\omega)| \underset{\omega \to 0}{=} O(\omega^m) \]
由于 \(|\hat{g}(\omega)| = |\hat{h}(\omega + \pi)|\),\(\psi\) 在 \(\omega = \pi\) 处有 \(m\) 阶零点当且仅当 \(\hat{h}\) 在 \(\omega = \pi\) 处有 \(m\) 阶零点。
支集的大小
另一个要求:\(\psi\) 的支集应足够小,以便内积仅捕获局部奇异性。
例如,我们可以要求 \(\psi\) 是紧支撑的。
- 若 \(\psi\) 是紧支撑的 \(\implies g = (g_n){n \in \mathbb{Z}}\) 和 \(\phi\) 是紧支撑的,因为:
\[ \frac{1}{\sqrt{2}} \psi(t/2) = \sum_{n=-\infty}^\infty g_n \phi(t - n) \]
- 若 \(g\) 是紧支撑的 \(\implies h = (h_n){n \in \mathbb{Z}}\) **是紧支撑的,因为:
\[ g_n = (-1)^{1-n} h{1-n}. \]
回忆以下公式:
\[ \frac{1}{\sqrt{2}} \phi(t/2) = \sum_{n=-\infty}^\infty h_n \phi(t - n) \]
假设 \(\text{supp } h = [N_1, N_2]\) 且 \(\text{supp } \phi = [K_1, K_2]\),应有\(\text{supp } \phi(\cdot/2) \subset [2K_1, 2K_2].\)
此外:\(\text{supp} \sum_{N_1}^{N_2} h_n \phi(t - n) \subset [N_1 + K_1, N_2 + K_2].\)
因此 \(K_1 = N_1\) 且 \(K_2 = N_2\)。
由于\(\frac{1}{\sqrt{2}} \psi(t/2) = \sum_n (-1)^{1-n} h_{1-n} \phi(t - n)\),小波\(\psi(\cdot/2)\) 的支集为 \([N_1 - N_2 + 1, N_2 - N_1 + 1]\)。
因此:
\[ \text{supp } \psi = [(N_1 - N_2 + 1)/2, (N_2 - N_1 + 1)/2], \]
\(\psi\) 的支集大小为 \(N_2 - N_1\),以 \(1/2\) 为中心。
Mallat 和 Meyer 定理
定理
令 \(\hat{h}\) 为 \(2\pi\) 周期函数,并满足以下要求:
- \(\hat{h}\) 在零的邻域内是 \(C^1\) 的;
- \(\inf_{\omega \in [-2\pi, 2\pi]} |\hat{h}(\omega)| > 0\);
- \(\forall \omega \in \mathbb{R}, \ |\hat{h}(\omega)|^2 + |\hat{h}(\omega + \pi)|^2 = 2\);
- \(\hat{h}(0) = \sqrt{2}\)。
则函数 \(\phi \in L^2(\mathbb{R})\),其傅里叶变换为:
\[ \hat{\phi}(\omega) = \prod_{j=1}^\infty \frac{\hat{h}(2^{-j}\omega)}{\sqrt{2}}, \quad \omega \in \mathbb{R}, \]
是一个尺度函数。
- 由于 \(\hat{h}(\omega) = \sum_{N_1}^{N_2} h_n e^{i\omega n}\),我们可以将 \(\hat{h}\) 写成 \(e^{i\omega}\) 的多项式,使用少量项。
- 此外\(\omega \mapsto \left(\frac{1 + e^{i\omega}}{2}\right)^k\)在 \(\omega = \pi\) 处具有 \(k\) 阶零点。
- 因此我们可以写为:
\[ \hat{h}(\omega) = \left(\frac{1 + e^{i\omega}}{2}\right)^m \gamma(\omega), \]
- 并优化 \(\gamma\),以保证 \(|\hat{h}(\omega)|^2 + |\hat{h}(\omega + \pi)|^2 = 2\),同时保持 \(N_2 - N_1\) 小。
- 通过此原则可以构造出大量小波。
经典小波
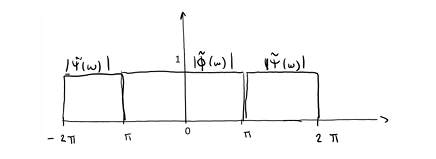
Shannon 小波
- \(\hat{\psi}\) 是紧支撑的 \(\implies \psi\) 具有无限多个消失矩。
- 然而,\(\psi\) 也是 \(C^\infty\) 的,在时域中具有较慢的衰减,这不利于逼近。
- 对于含间断点的函数 \(f\) 的逼近,会出现 Gibbs 效应。
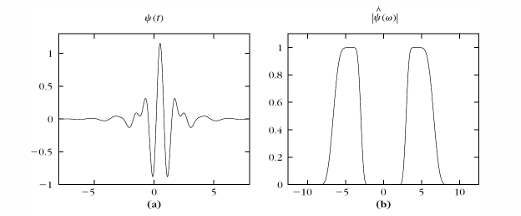
Meyer 小波
- 修复 Shannon 小波的问题:\(\hat{\psi}\) 是紧支撑且光滑的 \(\implies \psi\) 衰减更快。
Battle-Lemarié 小波
- 基于样条多分辨率导出的多项式样条小波。
- \(\psi\) 具有指数衰减。
- 对于 \(m\) 阶样条,\(\psi\) 具有 \(m+1\) 个消失矩。
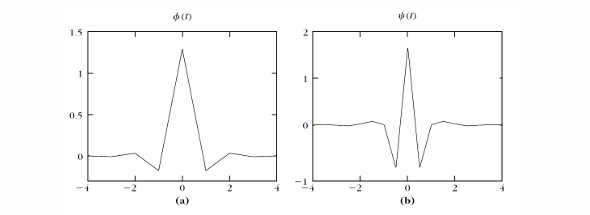
Daubechies 紧支撑小波
- 设计为在指定的消失矩数量下,具有最小的支撑大小。
- 对于 \(m = 1\) 的消失矩,得到 Haar 小波(所有小波中支撑最短)。
- 缺点:由于 \(h\) 的非线性相位,Daubechies 小波非常不对称。
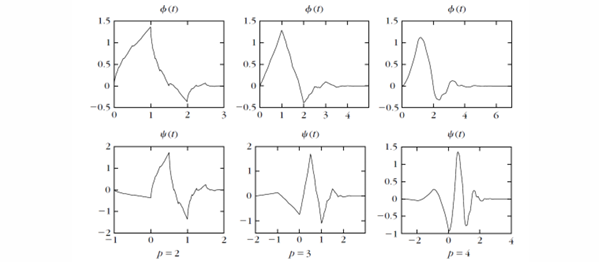
Symmlets 小波
- 修复 Daubechies 小波的问题: 提供短紧支撑,同时满足指定的消失矩数量,并具有近似线性相位(因此具有对称性)。
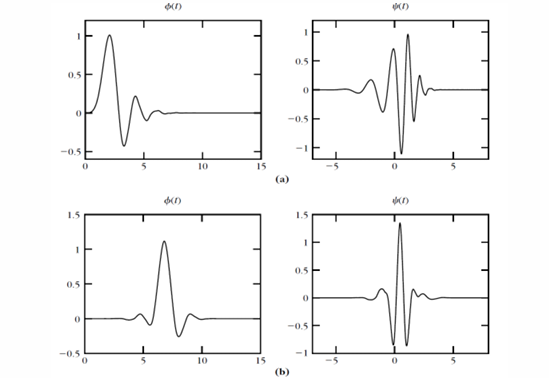
Coiflets 小波
- 提供短紧支撑,同时满足指定的消失矩数量,并具有近似线性相位(因此具有对称性)。
- \(\phi\)(尺度函数)也具有消失矩。

