从多分辨率到小波
从多分辨率到小波
PLAN
- 尺度函数(Scaling functions)
- 小波(Wavelets)
- Mallat 和 Meyer 定理的证明(Proof of the Mallat and Meyer’s theorem)
遗留问题
- Riesz 基没有正交性质 → 正交投影到 \(P_{V_j}\) 上是不实际的。
- 如何从 Riesz 基构造一个希尔伯特基(Hilbert basis)?
- 我们希望构造一个函数序列 \(\phi_{j, n}\),使得
\[ P_{V_j} f = \sum_{-\infty}^{\infty}\left(f, \phi_{j, n}\right) \phi_{j, n} \]
尺度函数 Scaling functions
定理
设 \((V_j)_{j ∈ ℤ}\) 是一个多分辨率,并定义一个尺度函数(scaling function) \(φ ∈ L^2(ℝ)\),其傅里叶变换满足:对于所有 \(ω ∈ ℝ\),
\[ \hat{\phi}(\omega) = \frac{\hat{\theta}(\omega)}{\left(\sum_{k=-\infty}^{+\infty} |\hat{\theta}(\omega + 2k\pi)|^2\right)^{1/2}} \]
同时定义函数
\[ \phi_{j,n} = \frac{1}{\sqrt{2^j}} \phi\left(\cdot - \frac{2^j n}{2^j}\right) \]
则,对于所有 \(j ∈ ℤ\),序列 \((\phi_{j,n})_{n ∈ ℤ}\) 是 \(V_j\) 的一个希尔伯特基。
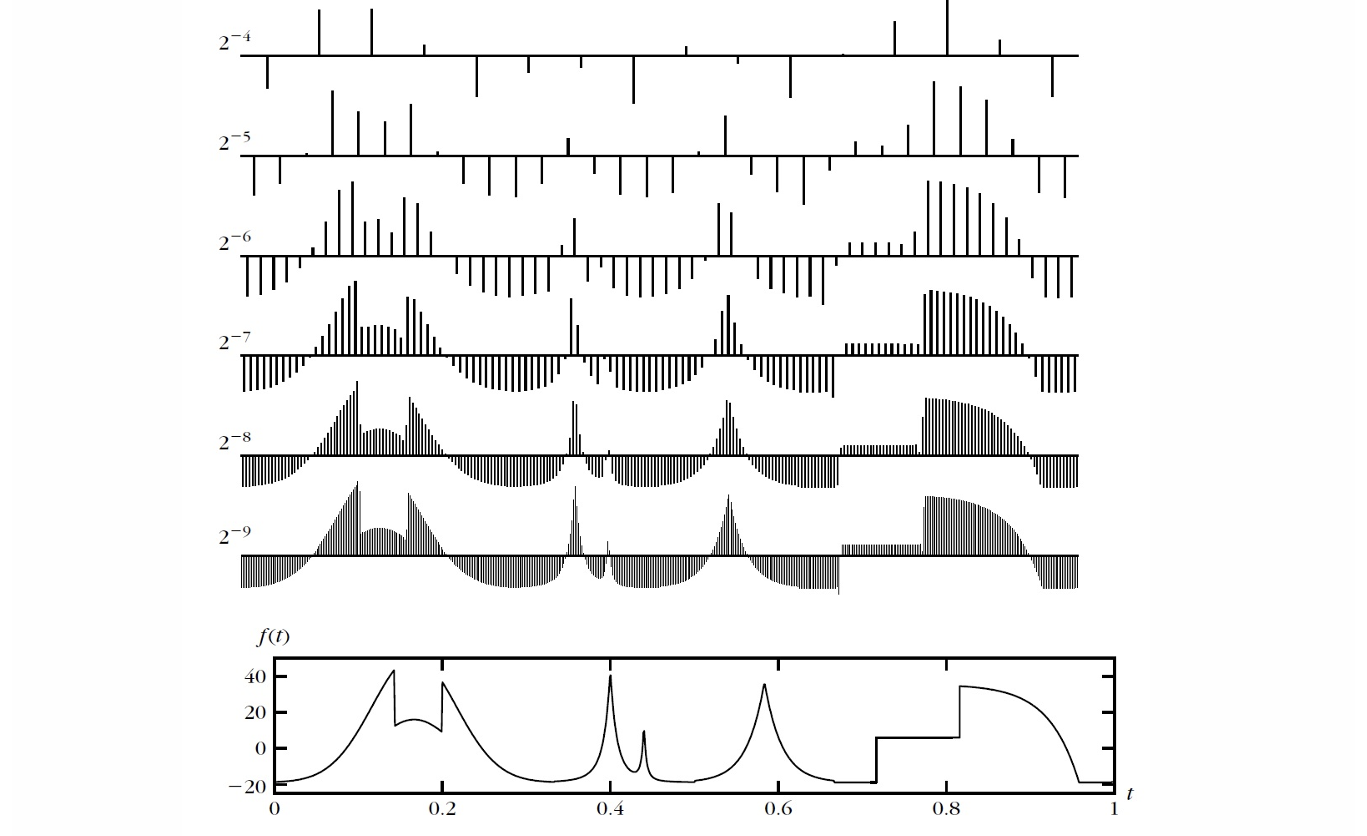
证明思路
根据多分辨率的定义,有:
\[ \phi \in V_0 \Longrightarrow \exists\left(a_n\right)_{n \in \mathbb{Z}} \text { 使得 } \phi=\sum_{n \in \mathbb{Z}} a_n \theta(\cdot-n) \]
通过傅里叶变换可得:
\[ \hat{\phi}(\omega)=\hat{a}(\omega) \hat{\theta}(\omega), \quad \omega \in \mathbb{R}, \]
其中:
\[ \hat{a}(\omega)=\sum_{n \in \mathbb{Z}} a_n e^{-i n \omega} \]
接下来需要在傅里叶域中表达 \((\phi(\cdot - n))_{n \in \mathbb{Z}}\) 的正交性。
定义 \(\tilde{\phi}\) 使得 \(\tilde{\phi}(t) = \overline{\phi}(-t)\)。于是,对于所有 \((n, p) \in \mathbb{Z}^2\),有:
\[ (\phi(\cdot - n), \phi(\cdot - p)) = \int_{-\infty}^\infty \phi(t - n) \overline{\phi}(t - p) \, dt = (\phi \ast \tilde{\phi})(n - p). \]
因此,\((\phi(\cdot - n))_{n \in \mathbb{Z}}\) 正交当且仅当:
\[ (\phi \ast \tilde{\phi})(n) = 1_{n = 0}. \]
注意:\(\phi \ast \tilde{\phi}\) 的傅里叶变换为:
\[ \omega \mapsto |\hat{\phi}(\omega)|^2. \]
通过采样 \(\gamma = \phi \ast \tilde{\phi}\),得到一个分布 \(\gamma_1\),其傅里叶变换为:
\[ \widehat{\gamma}_1(\omega)=\sum_{k=-\infty}^{\infty} \widehat{\gamma}(\omega-2 k \pi) \]
因此,正交性等价于:
\[ \sum_{k = -\infty}^\infty |\hat{\phi}(\omega + 2k\pi)|^2 = 1, \quad \omega \in \mathbb{R}. \]
这意味着我们必须选择:
\[ \hat{a}(\omega) = \left( \sum_{k = -\infty}^\infty |\hat{\theta}(\omega + 2k\pi)|^2 \right)^{-1/2}. \]
示例
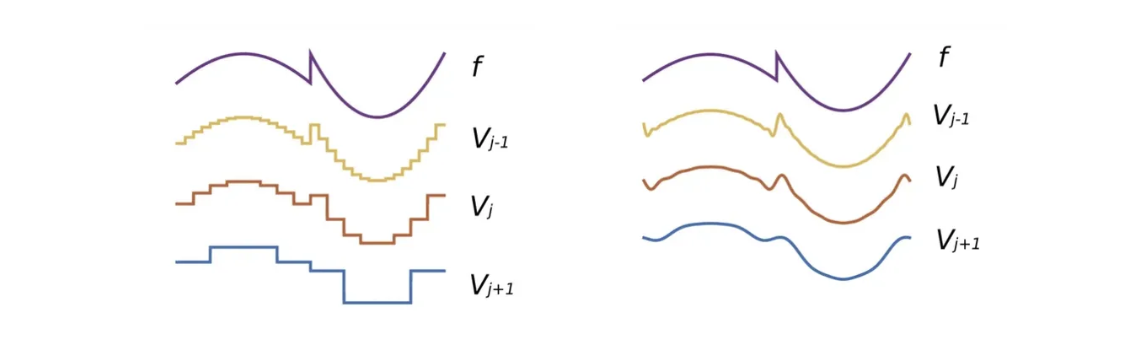
分段常数多分辨率
\(\theta=\mathbb{1}_{[0,1[ }\), 导致 Riesz 基 \((\theta(\cdot - n)){n \in \mathbb{Z}}\) 是正交的。
因此,\(\phi = \theta\),并且生成的函数 \(\phi_{j,n}\) 形成 \(V_j\) 的希尔伯特基,如前所示。
Shannon 多分辨率
\(\theta : t \mapsto \frac{\sin(\pi t)}{\pi t}\), 导致 \((\theta(\cdot - n))_{n \in \mathbb{Z}}\) 是正交 Riesz 基。
因此,设 \(\phi = \theta\)。
样条多分辨率
通过卷积/乘积规则计算傅里叶变换,并应用上述定理。
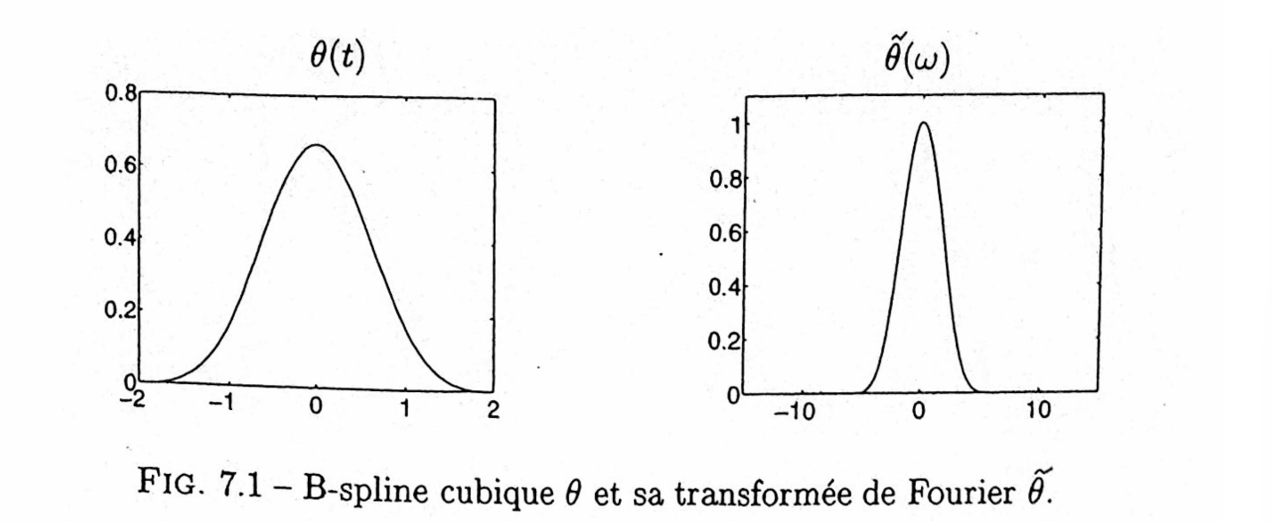
\[ \tilde{\theta}_m(\omega) = \left( \frac{\sin(\omega/2)}{\omega/2} \right)^{m+1} \exp \left( -i \varepsilon \frac{\omega}{2} \right), \]
其中:
\[ \varepsilon = \begin{cases} 1, & m \text{ 为偶数}, \\ 0, & m \text{ 为奇数}. \end{cases} \]
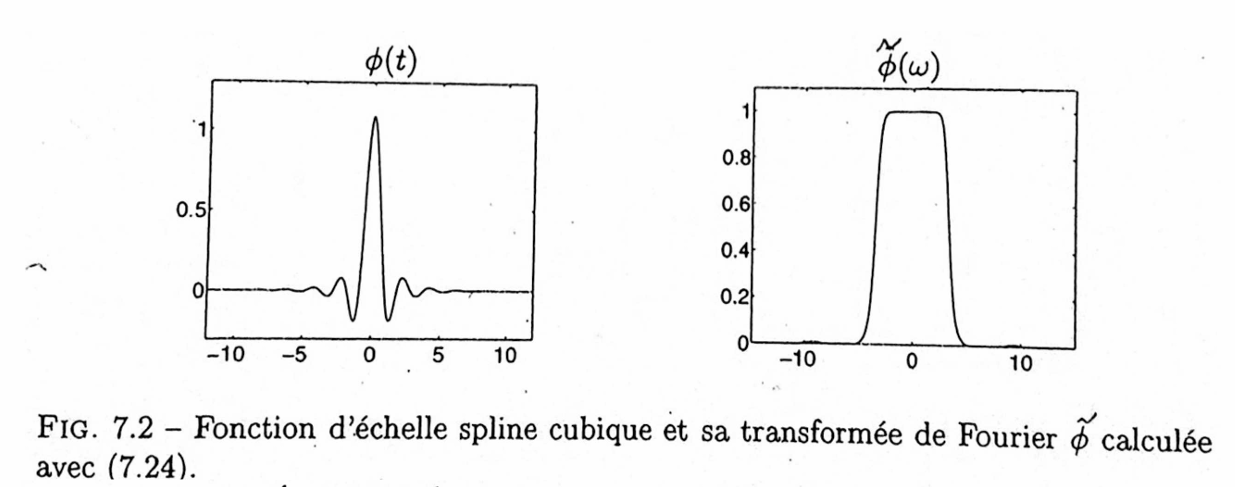
\[ \hat{\phi}(\omega) = \frac{\exp \left( -i \varepsilon \frac{\omega}{2} \right)}{\omega^{m+1} \sqrt{S_{2,m+2}(\omega)}}, \]
其中:
\[ S_m(\omega) = \sum_{\ell = -\infty}^\infty \frac{1}{(\omega + 2\ell\pi)^m}. \]
具体示例:对于 \(S_8(2\omega)\),有:
\[ S_8(2\omega) = \frac{5 + 30 \cos^2(\omega) + 30 \sin^2(\omega) \cos^2(\omega)}{105 \cdot 2^8 \sin^8(\omega)} + \frac{70 \cos^4(\omega) + 2 \sin^4(\omega) \cos^2(\omega) + \frac{2}{3} \sin^6(\omega)}{105 \cdot 2^8 \sin^8(\omega)}. \]
总结
多分辨率
多分辨率是一系列希尔伯特子空间 \((V_j)_{j \in \mathbb{Z}}\),用于描述在尺度 \(2^j\) 下的函数。
子空间的特性
每个 \(V_j\) 由 \(V_0\) 的一个 Riesz 基 \((\theta(\cdot - n))_{n \in \mathbb{Z}}\) 所表征,例如分段常数、样条等。
尺度函数
通过对 \((\theta(\cdot - n)),{n \in \mathbb{Z}}\) 进行正交化,我们可以导出一个尺度函数 \(\phi\),它生成 \(V_j\) 的希尔伯特基 \(\{\phi_{j,n}\}_{n \in \mathbb{Z}}\)。这些基函数由 \(\phi\) 通过尺度和平移得到:
\[ \phi_{j,n} = \frac{1}{\sqrt{2^j}} \phi\left(\cdot - \frac{2^j n}{2^j}\right). \]
多分辨率的意义
多分辨率的概念使得我们可以在不同尺度下构建 \(f\) 的近似层次结构,从而保证无信息丢失。但这对压缩有何用处?
小波 Wavelets
主要思想 main idea
对于 \(j \in \mathbb{Z}\),构造一个 Hilbert 子空间 \(W_{j+1}\),使得
\[ V_{j+1} \oplus W_{j+1} = V_j \]
因此,对于任意 \(f \in L^2(\mathbb{R})\),满足
\[ P_{V_j}f = P_{V_{j+1}}f + P_{W_{j+1}}f \]
即,\(P_{W_{j+1}}f\) 包含了 \(f\) 在尺度 \(2^j\) 存在但在尺度 \(2^{j+1}\) 消失的细节信息。
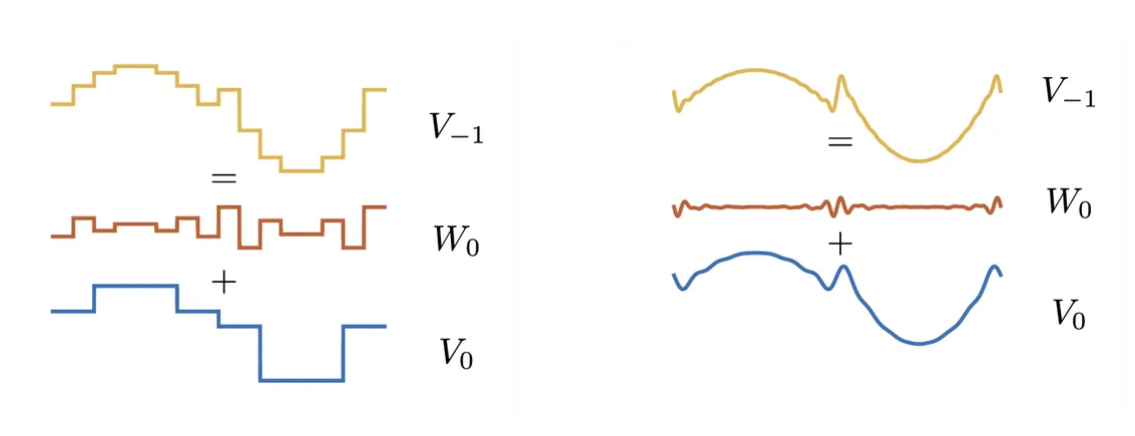
事实上,我们可以理解为:
- \(P_{V_{j+1}}f\) 对应于通过低通滤波器 (low-pass filter) 对 \(P_{V_j}f\) 进行滤波。
- \(P_{W_{j+1}}f\) 对应于通过高通滤波器 (high-pass filter) 对 \(P_{V_j}f\) 进行滤波。
共轭镜像滤波器 Conjugate Mirror Filter
定义
令 \(\phi \in L^2(\mathbb{R})\) 是一个尺度函数。对所有 \(n \in \mathbb{Z}\),定义:
\[ h_n = \left( \frac{1}{\sqrt{2}} \phi(\cdot / 2), \phi(\cdot - n) \right) \]
这些是 \(\frac{1}{\sqrt{2}} \phi(\cdot / 2)\) 在 \(V_1\) 上投影到 \(V_0\) 的系数:
\[ \frac{1}{\sqrt{2}} \phi(\cdot / 2) = \sum_n h_n \phi(\cdot - n) \]
序列 \((h_n)_{n \in \mathbb{Z}}\) 是一个低通滤波器 (low-pass filter) 的冲激响应,称为共轭镜像滤波器 (conjugate mirror filter)。
注记
\[ \frac{1}{\sqrt{2}} \phi(\cdot / 2) = \sum_n h_n \phi(\cdot - n) \implies \sqrt{2} \widehat{\phi}(2\omega) = \widehat{\phi}(\omega) \cdot \left( \sum_n h_n e^{-i n \omega} \right), \quad \omega \in \mathbb{R} \tag{1} \]
通过对两边取傅里叶变换,考虑傅里叶级数
\[ \widehat{h}(\omega) = \sum_n h_n e^{-i n \omega}, \quad \omega \in \mathbb{R} \]
傅里叶级数是 \(2\pi\)-周期的)。
我们可以将 \((1)\) 重写为:
\[ \widehat{\phi}(2\omega) = \widehat{\phi}(\omega) \frac{\widehat{h}(\omega)}{\sqrt{2}}, \quad \omega \in \mathbb{R} \]
示例
Shannon 多分辨率 (Shannon Multiresolution):
- \(\widehat{\phi} = \mathbf{1}_{[-\pi, \pi]}\)。
- 因此,\(\forall \omega \in [-\pi, \pi]\):
\[ \mathbb{1}_{[-\pi / 2, \pi / 2]}=\mathbb{1}_{[-\pi, \pi]} \widehat{h}(\omega) / \sqrt{2} \]
- 由此可得,\(\forall \omega \in [-\pi, \pi]\):
\[ \widehat{h}(\omega) = \sqrt{2} \cdot \mathbf{1}_{[-\pi/2, \pi/2]}(\omega). \]
分段常值多分辨率 (Piecewise Constant Multiresolution):
\(\phi = \mathbf{1}_{[0, 1]}\)。
由
\[ h_n = \left( \frac{1}{\sqrt{2}} \phi(\cdot / 2), \phi(\cdot - n) \right), \]
得
\[ h_n = \begin{cases} 2^{-1/2}, & \text{如果 } n = 0, 1, \\ 0, & \text{其他情况}. \end{cases} \]
这有时被称为局部平均 (local average)。
样条多分辨率 (Spline Multiresolution):
对于 \(m\) 阶 box 样条, \(\widehat{\phi}\) 的表达式
\[ \hat{\phi}(\omega) = \frac{\exp \left( -i \varepsilon \frac{\omega}{2} \right)}{\omega^{m+1} \sqrt{S_{2,m+2}(\omega)}}, \]
代入\(\widehat{\phi}(2\omega) = \widehat{\phi}(\omega) \frac{\widehat{h}(\omega)}{\sqrt{2}}, \quad \omega \in \mathbb{R}.\)
得,\(\forall \omega \in \mathbb{R}\):
\[ \widehat{h}(\omega) = \exp\left(-\frac{i \omega}{2}\right) \sqrt{\frac{S_{2m+2}(\omega)}{2^{m+1} S_{2m+2}(2\omega)}}. \]

高通滤波器的构造
- 令 \(\phi \in L^2(\mathbb{R})\) 为一个尺度函数,\((h_n)_{n \in \mathbb{Z}}\) 为相应的共轭镜像滤波器。
- 定义一个滤波器 \((g_n)_{n \in \mathbb{Z}}\),其傅里叶变换满足以下条件:
\[ \widehat{g}(\omega) = e^{-i\omega} \widehat{h}(\omega + \pi), \quad \forall \omega \in \mathbb{R}. \]
注记
- 根据傅里叶变换的性质:
\[ g_n = (-1)^{1-n} h_{1-n}, \quad \forall n \in \mathbb{Z}. \]
\((g_n)\) 是一个高通滤波器 (high-pass filter),因为:
\[ |\widehat{g}(\omega)| = |\widehat{h}(\omega + \pi)|, \]
且 \(\widehat{h}\) 是 \(2\pi\)-周期函数。
Mallat-Meyer定理
令 \(\phi \in L^2(\mathbb{R})\) 为一个尺度函数,\((g_n)_{n \in \mathbb{Z}}\) 为对应的滤波器(如前述定义)。考虑函数 \(\psi \in L^2(\mathbb{R})\),称为小波函数 (wavelet function),其傅里叶变换满足:
\[ \widehat{\psi}(2\omega) = \frac{\widehat{\phi}(\omega) \widehat{g}(\omega)}{\sqrt{2}}, \quad \forall \omega \in \mathbb{R}. \]
此外,对于所有 \((j, n) \in \mathbb{Z}^2\),定义:
\[ \psi_{j, n}(t) = \frac{1}{\sqrt{2^j}} \psi \left( \frac{t - 2^j n}{2^j} \right). \]
则,对于任意 \(j \in \mathbb{Z}\) 和对应的尺度 \(s = 2^j\),集合 \(\{\psi_{j, n}\}_{n \in \mathbb{Z}}\) 是子空间 \(W_j\) 的一个Hilbert 基。
此外,对于整体尺度范围,集合 \(\{\psi_{j, n}\}_{(j, n) \in \mathbb{Z}^2}\) 是 \(L^2(\mathbb{R})\) 的一个称为小波基 (wavelet basis) 的 Hilbert 基。
\(\psi(\cdot / 2) \in W_1 \subset V_0\),因此存在 \((g_n){n \in \mathbb{Z}}\) 使得:
\[ \frac{1}{\sqrt{2}} \psi(\cdot / 2) = \sum{n = -\infty}^\infty g_n \phi(\cdot - n), \]
其中:
\[ g_n = \left( \frac{1}{\sqrt{2}} \psi(\cdot / 2), \phi(\cdot - n) \right). \]
取傅里叶变换:
\[ \widehat{\psi}(2\omega) = \frac{\widehat{\phi}(\omega) \widehat{g}(\omega)}{\sqrt{2}}, \quad \omega \in \mathbb{R}. \]
示例
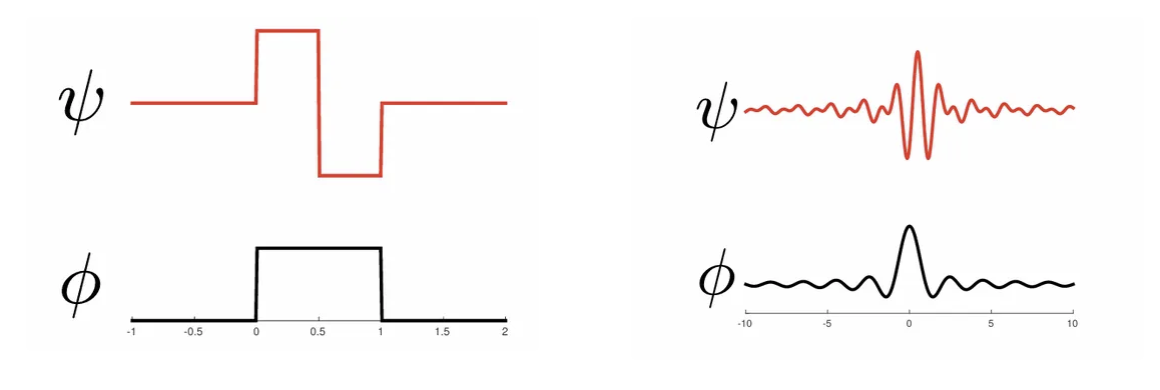
Haar 小波 (Haar Wavelets)
尺度函数 (Scaling Function):
\[ \phi = \mathbf{1}_{[0, 1]} \]
共轭镜像滤波器 (Conjugate Mirror Filter):
\[ h_n = \begin{cases} 2^{-1/2}, & \text{if } n = 0, 1, \\ 0, & \text{otherwise.} \end{cases} \]
滤波器 \((g_n)\):
\[ g_n = \begin{cases} -2^{-1/2}, & \text{if } n = 0, \\ 2^{-1/2}, & \text{if } n = 1, \\ 0, & \text{otherwise.} \end{cases} \]
小波函数 (Wavelet):
\[ \psi(t) = \begin{cases} -1, & \text{if } 0 \leq t < 1/2, \\ 1, & \text{if } 1/2 \leq t < 1, \\ 0, & \text{otherwise.} \end{cases} \]
Shannon 小波 (Shannon Wavelets)
尺度函数 (Scaling Function):
\[ \phi(t) = \frac{\sin(\pi t)}{\pi t} \]
共轭镜像滤波器 (Conjugate Mirror Filter):
\[ \widehat{h}(\omega) = \sqrt{2} \cdot \mathbf{1}_{[-\pi/2, \pi/2]}(\omega) \]
滤波器 \((g_n)\):
\[ \widehat{g}(\omega) = \begin{cases} e^{-i\omega/2}, & \text{if } \omega \in [-2\pi, \pi] \cup [\pi, 2\pi], \\ 0, & \text{otherwise.} \end{cases} \]
小波函数 (Wavelet):
\[ \psi(t) = \frac{\sin(2\pi(t - 1/2))}{\pi(t - 1/2)} - \frac{\sin(\pi(t - 1/2))}{\pi(t - 1/2)}. \]
Battle-Lemarié / Cubic Spline 小波
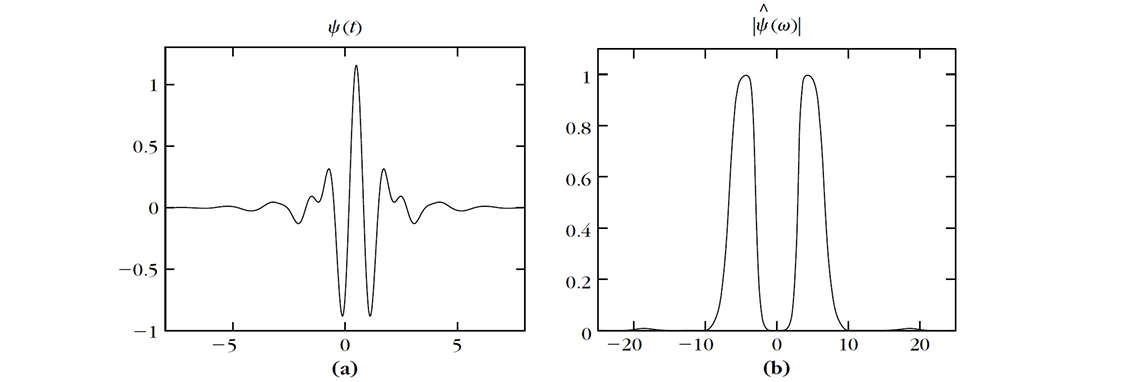
\(L^2(\mathbb{R})\) 的分解
Parseval 等式: 对于 \(f \in L^2(\mathbb{R})\),
\[ f = \sum_{j \in \mathbb{Z}} P_{W_j}f = \sum_j \sum_n \langle f, \psi_{j,n} \rangle \psi_{j,n}. \]
\(f\) 是通过不同尺度的子空间 \(W_j\) 分解成多个分量的和。
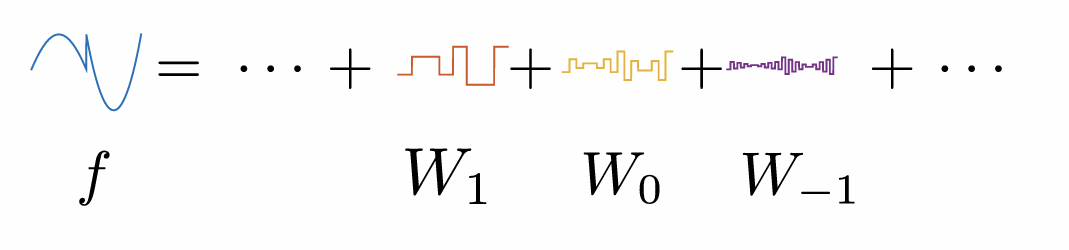
另一种 Hilbert 空间分解
Hilbert 空间的表达:
\[ L^2(\mathbb{R}) = V_J \oplus \bigoplus_{j=J}^{\infty} W_j, \]
其中 \(J\) 是某个粗略尺度。
对于任意 \(f \in L^2(\mathbb{R})\),
\[ \begin{aligned} f & =P_{V_J} f+\sum_{j=-\infty}^J P_{W_j} f \\ & =\sum_{n=-\infty}^{\infty}\left(f, \phi_{J, n}\right) \phi_{J, n}+\sum_{j=-\infty}^J \sum_{n=-\infty}^{\infty}\left(f, \psi_{j, n}\right) \psi_{j, n} \end{aligned} \]
Mallat-Meyer定理的证明
定理1
对于共轭镜像滤波器 \((h_n)_{n \in \mathbb{Z}}\),其傅里叶变换(傅里叶级数形式)表示为:
\[ \widehat{h}(\omega) = \sum{n} h_n e^{-i n \omega}, \quad \omega \in \mathbb{R}, \]
满足以下性质:
对于任意 \(\omega \in \mathbb{R}\):
\[ |\widehat{h}(\omega)|^2 + |\widehat{h}(\omega + \pi)|^2 = 2. \]
\(\widehat{h}(0) = \sqrt{2}.\)
定理 2
反之,令 \(\widehat{h}\) 是一个 \(2\pi\)-周期函数,并满足以下条件:
\(\widehat{h} \in C^1\) 在零点邻域中连续可导;
在 \(\omega \in [-2\pi, 2\pi]\) 内有 \(\inf |\widehat{h}(\omega)| > 0\);
对于任意 \(\omega \in \mathbb{R}\):
\[ |\widehat{h}(\omega)|^2 + |\widehat{h}(\omega + \pi)|^2 = 2; \]
\(\widehat{h}(0) = \sqrt{2}.\)
则傅里叶变换为
\[ \widehat{\phi}(\omega) = \prod_{j=1}^\infty \frac{\widehat{h}(2^{-j}\omega)}{\sqrt{2}}, \quad \omega \in \mathbb{R}, \]
的函数 \(\phi \in L^2(\mathbb{R})\) 是一个尺度函数。
证明
假设 \((h_n)\) 是一个共轭镜像滤波器:
\[ \widehat{\phi}(2\omega) = \frac{\widehat{\phi}(\omega) \widehat{h}(\omega)}{\sqrt{2}}, \quad \omega \in \mathbb{R}. \]
对任意 \(p \in \mathbb{Z}\),有:
\[ \widehat{\phi}(2^{p+1}\omega) = \frac{\widehat{\phi}(2^p\omega)\widehat{h}(2^p\omega)}{\sqrt{2}}. \]
- 反复迭代,得到
\[ \widehat{\phi}(\omega) = \prod_{p=1}^K \frac{\widehat{h}(2^{-p}\omega)}{\sqrt{2}} \cdot \widehat{\phi}(2^{-K}\omega). \]
- 当 \(K \to \infty\) 时,\(\widehat{\phi}(2^{-K}\omega) \to 1\),因此:
\[ \widehat{\phi}(\omega) = \prod_{p=1}^\infty \frac{\widehat{h}(2^{-p}\omega)}{\sqrt{2}}. \]
Hilbert 基的正交归一性
- 归一性关系
\[ \sum_{k=-\infty}^\infty |\widehat{\phi}(\omega + 2k\pi)|^2 = 1, \quad \omega \in \mathbb{R}. \]
该公式表达了 \((\phi(\cdot - n))_{n \in \mathbb{Z}}\) 的 Hilbert 基正交归一性。
带入 \(\widehat{\phi}(2\omega) = \frac{\widehat{\phi}(\omega)\widehat{h}(\omega)}{\sqrt{2}}\):
\[ \sum_{k=-\infty}^\infty \left| \widehat{h}\left(\frac{\omega}{2} + k\pi\right) \right|^2 \cdot \left| \widehat{\phi}\left(\frac{\omega}{2} + k\pi\right) \right|^2 = 2. \]
使用 \(k = 2p\) 或 \(k = 2p+1\) 进行拆分,重新排列得到:
\[ \left|\widehat{h}\left(\frac{\omega}{2}\right)\right|^2 \sum_{p=-\infty}^\infty \left|\widehat{\phi}\left(\frac{\omega}{2} + 2p\pi\right)\right|^2 + \left|\widehat{h}\left(\frac{\omega}{2} + \pi\right)\right|^2 \sum_{p=-\infty}^\infty \left|\widehat{\phi}\left(\frac{\omega}{2} + (2p+1)\pi\right)\right|^2 = 2. \]
再次带入
对 \(\omega' = \frac{\omega}{2}\) 或 \(\omega' = \frac{\omega}{2} + \pi\),最终得到:
\[ |\widehat{h}(\omega')|^2 + |\widehat{h}(\omega' + \pi)|^2 = 2. \]
- 结论 \(|\widehat{h}(\omega)|^2 + |\widehat{h}(\omega + \pi)|^2 = 2\) 是 \((\phi(\cdot - n))_{n \in \mathbb{Z}}\) 成为 Hilbert 基的必要条件。
- 它对应于正交归一要求,保证尺度函数 \(\phi\) 的构造正确。
Hilbert 基的构造
为了证明 \((\psi(\cdot - n))_{n \in \mathbb{Z}}\) 是 \(W_0\) 的 Hilbert 基,需要使用以下引理。
引理
- 序列 \((\psi_{j,n})_{n \in
\mathbb{Z}}\) 是 \(W_j\) 的
Hilbert 基,当且仅当以下两个条件成立:
\(\widehat{g}(\omega)\) 满足归一性:
\[ |\widehat{g}(\omega)|^2 + |\widehat{g}(\omega + \pi)|^2 = 2. \]
\(\widehat{g}(\omega)\) 与 \(\widehat{h}(\omega)\) 的正交性条件:
\[ \widehat{g}(\omega) \widehat{h}^*(\omega)+\widehat{g}(\omega+\pi) \widehat{h}^*(\omega+\pi)=0 \]
- 解释:
- 条件 (i) 对应于 \((\psi(\cdot - n))_{n \in \mathbb{Z}}\) 的正交归一性。
- 条件 (ii) 保证 \(W_0\) 与 \(V_0\) 正交,即 \((\psi, \phi(\cdot - n)) = 0\) 对于所有 \(n \in \mathbb{Z}\)。

