块傅里叶基和JPEG

块傅里叶基，是一种用于表示信号的时间-频率基。这些基的使用有两种主要的理由：其一，基于函数分解的正则性，系数呈递减趋势；其二，可将其解释为卡尔霍宁-洛厄夫 (Karhunen-Loève) 基（或某种近似），用于特定的随机过程建模。

连续时间

傅里叶级数

复指数函数族 \(e_n(t)=\exp (i 2 \pi n t)\) （其中 \(n \in \mathbb{Z}\) ) 是定义在 \(L_2(0,1)\) 上的一个正交基。这使得可以在 \(L_2(0,1)\) 空间中定义傅里叶级数:

$$

F_n=_0^1 f e_n^* d t =_0^1 f(t) (-i 2 n t) d t

$$

重建公式 (Reconstruction)：

\[ f=\sum_{n \in \mathbb{Z}} F_n e_n \]

傅里叶级数按 \(L_2\) 意义上收敛，即：

\[ \lim _{N \rightarrow \infty}\left\|f-\sum_{n=-N}^N F_n e_n\right\|_2^2=0 \]

但这并不保证简单或一致收敛。 分解系数 \(F_n\) 的递减速度至少与 \(f\) 的 Sobolev意义下的正则性相关。

回顾：如果一个函数 \(f\) 属于 Sobolev空间 \(H_s\) ，则它属于 \(L_2\) ，并且它的导数直到 \(s\) 阶都是可定义的。此外，如果 \(f\) 的支撑严格包含在 \(] 0,1[\) 中，则:

\[ \sum_{n \in \mathbb{Z}} n^{2 s}\left|F_n\right|^2<\infty \]

我们有：\(F_n^{(s)}=(-2 i \pi n)^s F_n\)，且\(f^{(s)} \in L_2(0,1)\)。假设\(f\)的支撑严格包含在\(]0,1[\)。观察：

\[ \varepsilon_N=\left\|f-f_N\right\|_2^2=o\left(N^{-2 s}\right) \]

块傅里叶基

为了从 \(L_2(0,1)\) 上的基扩展到 \(L_2(\mathbb{R})\) ，需要在整个实数轴上表示函数。具体方法是将定义在 \([0,1]\) 区间内的函数 \(f\) 进行分段扩展：将其分割为多个区间 \([m, m+1]\) 的函数片段，每个片段由函数 \(f\) 在 \([0,1]\) 上的行为通过平移实现：

\[ g = f_{1,[m, m+1]}, \ g\in L_2(\mathbb{R}) \]

由于函数通常没有理由满足周期性条件，因此系数的递减通常非常缓慢。

余弦基 Bases de cosinus

为了获得令人满意的递减性质，可以使用余弦基。

Neumann-Neumann 余弦基

\[ c_n(t)=\lambda_n \sqrt{2} \cos (\pi n t), \quad avec \quad \lambda_0=\sqrt{2} , \ \lambda_n=1 \text { si } n>0 \text {. } \]

Neumann-Neumann 余弦基满足 Neumann 边界条件，即基函数的导数在边界处为零。这对应于函数的平滑延拓，避免了周期性假设下可能出现的不连续性问题。

由于余弦基在边界处是平滑的，分解的系数\(F_n\)能以较快速度递减。这种性质弥补了块式傅里叶基在边界处引入不连续性的问题

Neumann-Dirichlet 余弦基

\[ c_n(t)=\sqrt{2} \cos (\pi(n+1 / 2) t), \quad n \geq 0 \]

该余弦基在 \([0,1]\) 的两端分别满足不同的边界条件：

  • 在 \(t=0\) ，满足 Neumann 边界条件（导数为零）。
  • 在 \(t=1\) ，满足 Dirichlet 边界条件（函数值为零）。
  • 这意味着函数在一端光滑，但在另一端具有较强的约束（函数值为零）。

Neumann-Dirichlet 余弦基通常无法恢复快速递减的傅里叶系数，因为它在边界 \(t=1\) 的 Dirichlet 条件会引入较大的不连续性。这种不连续性影响了系数的平滑性和递减速度。

有限维度

在本文中，向量的索引从 0 开始。

离散傅里叶变换（Transformée de Fourier discrète，简称 TFD）

向量族 \(\left(e_m\right)_{m=0, \ldots, N-1}\) 的定义为:

\[ e_m=(1, \ldots, \exp (i 2 \pi n m / N), \ldots, \exp (i 2 \pi(N-1) m / N)), \]

该族在常数因子上是复数域 \(\mathbb{C}^N\) 中的一个正交基。 维度为 \(N\) 的向量 \(\mathbf{x}\) 的离散傅里叶变换（TFD）通过以下基变换给出：

\[ \begin{gathered} \mathbf{F}_{n m}=\exp (-i 2 \pi n m / N) \\ \mathbf{X}=\mathbf{F} \mathbf{x}, \\ X_m=\sum_{n=0}^{N-1} x_n \exp \left(-i 2 \pi n m / N\right), \\ x_n=\frac{1}{N} \sum_{k=0}^{N-1} X_m \exp (i 2 \pi n m / N) \end{gathered} \]

其中\(F\)有\(FF^H = NI\)

离散傅里叶变换可以看作一种 Karhunen-Loève 基。对于协方差矩阵是循环矩阵的随机向量，傅里叶基正是其 Karhunen-Loève 基。

DCT-I 和 DCT-III：DCT-I 和 DCT-III 的性质与 DCT-II 和 DCT-IV 相似，但它们的对称性和索引定义不同。例如，DCT-I 的对称点为 \(0\) 而非 \(-1 / 2\) 。

DCT-II 是最常用的变换类型，广泛用于图像压缩（如 JPEG）和信号处理。

DCT-IV 的应用相对较少，但在某些特定场景下，如需要额外的紧凑性或特定边界条件时，是一种有效的选择。

DCT-II 离散余弦变换-II

DCT-II的基向量为：

\[ c_{m n}^{\mathrm{II}}=\lambda_m \sqrt{\frac{2}{N}} \cos \left(\frac{m \pi}{N}\left(n+\frac{1}{2}\right)\right) \]

其中:

  • \(\lambda_0=\sqrt{2}\) ，此外 \(\lambda_m=1\) ；
  • \(N\) 是向量维度；
  • \(m, n\) 分别是基向量和数据的索引。
  • 对于大的 \(N\) ，DCT-II 基逐渐接近于平稳过程的 Karhunen-Loève 基。这表明，DCT-II 在统计意义上是最优的，用于分解和表示平稳信号。
  • 类似于 Neumann-Neumann 余弦基，DCT-II 通过改变基，可以有效处理非周期信号，且分解系数 \(c_{m n}\) 的递减性质依然良好。

DCT-IV（离散余弦变换-IV）

DCT-IV的基向量为：

\[ c_{m n}^{\mathrm{IV}}=\sqrt{\frac{2}{N}} \cos \left(\frac{\pi}{N}\left(m+\frac{1}{2}\right)\left(n+\frac{1}{2}\right)\right) \]

  • DCT-IV 通常不会单独使用，而是用于更紧凑地计算 DCT-II，或者用于 Neumann-Dirichlet 基的连续版本。

JPEG编码

JPEG格式是目前最常用的有损图像压缩格式之一。

编码算法分为以下步骤：

  • 基于减少熵的分解信号；
  • 量化；
  • 编码。

每个编码器因这三个步骤的实现选择而有所不同。

为了进行图像编码，添加了一个颜色处理的初始步骤。

颜色处理

描述像素的三个RGB（红、绿、蓝）值被替换为 \(Y^{\prime}, C_B, C_R\) (亮度和两个色度值），定义如下：

\[ \begin{gathered} Y^{\prime}=\left(0.299 \cdot R_D^{\prime}\right)+\left(0.587 \cdot G_D^{\prime}\right)+\left(0.114 \cdot B_D^{\prime}\right) \\ C_B=128-\left(0.168736 \cdot R_D^{\prime}\right)-\left(0.331264 \cdot G_D^{\prime}\right)+\left(0.5 \cdot B_D^{\prime}\right) \\ C_R=128+\left(0.5 \cdot R_D^{\prime}\right)-\left(0.418688 \cdot G_D^{\prime}\right)-\left(0.081312 \cdot B_D^{\prime}\right) \end{gathered} \]

逆变换为：

\[ \begin{gathered} R_D^{\prime}=Y^{\prime}+1.402 \cdot\left(C_R-128\right) \\ G_D^{\prime}=Y^{\prime}-0.344136 \cdot\left(C_B-128\right)-0.714136 \cdot\left(C_R-128\right) \\ B_D^{\prime}=Y^{\prime}+1.772 \cdot\left(C_B-128\right) \end{gathered} \]

这里的RGB值经过了非线性校正，因此标记为'。 这种转换可以部分解耦三个通道，并将人眼非常敏感的亮度信息与颜色信息分开。颜色信息随后可以以因子2进行下采样。

信号分解

用于信号分解的最优基是 Karhunen-Loève（卡尔霍宁-洛伊夫）基。然而，它取决于图像模型，并且通常没有允许快速计算的结构。

因此，一般更倾向于使用基于 \(8 \times 8\) 块的二维DCT-II（离散余弦变换II）。如上所述，DCT对于平稳过程近似于Karhunen-Loève基，并且可以高效计算。

下面的代码提供了一个例子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def dct8(img):
    step = 8
    d = np.zeros(img.shape)
    Nx = img.shape[0]//step
    Ny = img.shape[1]//step
    
    for n in range(Nx):
        for m in range(Ny):
            patch = img[step * n : step * (n + 1), step * m : step * (m+ 1)]
            d[step * n : step * (n + 1), step * m : step * (m+ 1)] = fft.dctn(patch, norm='ortho')
            
    return d

def idct8(img):
    step = 8
    d = np.zeros(img.shape)
    Nx = img.shape[0]//step
    Ny = img.shape[1]//step
    
    for n in range(Nx):
        for m in range(Ny):
            patch = img[step * n : step * (n + 1), step * m : step * (m+ 1)]
            d[step * n : step * (n + 1), step * m : step * (m+ 1)] = fft.idctn(patch, norm='ortho')
            
    return d

分解后的熵将有效减少

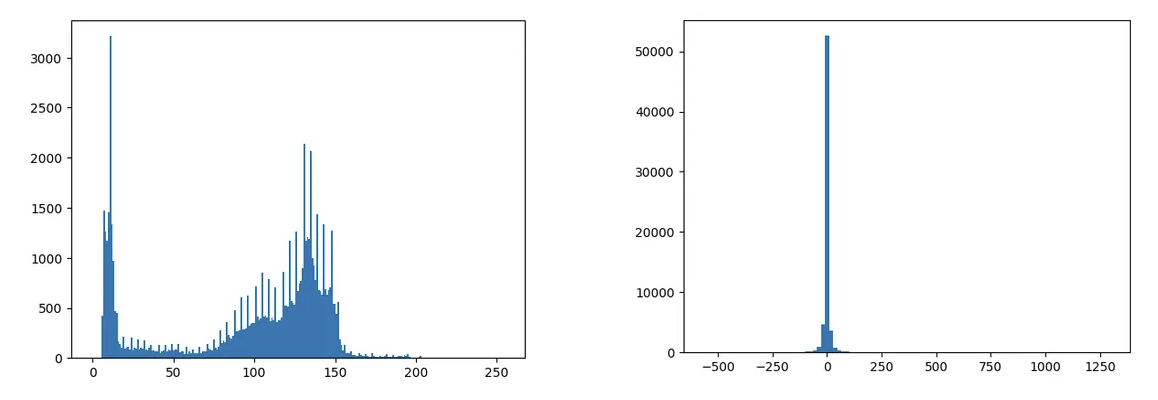
量化

在JPEG格式中，量化可以根据系数使用不同的权重。这是为了考虑人眼对不同频率的敏感性。

实际上，定义具有权重 \(w_n^2\) 的量化误差为:

\[ d=\sum_{n=1}^N \frac{d_n}{w_n^2}, \]

这等价于将前面课程中的定理应用于加权系数 \(X_n^w=X_n / w_n\) 。 因此，量化步长为 \(\Delta_n=w_n \Delta\)。 对总误差影响最小的系数被粗略量化。 这些量化步长由编码器根据用户提供的质量目标确定，并存储在文件中。 通常，量化步长随频率增加。每个编码器使用的量化参数不同，因此不同编码器的参数并不具有相同的效果。

编码

目的是降低系数的熵，但必须很好地对其进行编码才能实现这一目的。

DCT（离散余弦变换）中平均值系数（第一个系数）单独编码，方法是对连续系数之间的差值进行编码。

对于其他系数，由于系数递减与量化步长随频率增大的结合，会出现大量零系数。这些系数按照之字形顺序存储，以使零序列尽可能长。

使用以下编码规则：

  • 4位编码系数数量 \(Z\)，即在第一个非零系数前的零数量；
  • 4位编码用于编码系数的位数 \(L\)；
  • \(L\) 位用于编码系数的值。

特例：

  • \(（15, 0）\)编码16个零系数的序列；
  • \(（0, 0）\)表示一个块的结束，当最后的系数全为零时。

成对的 \((Z,L)\)使用由编码器确定的霍夫曼编码（Huffman code）存储在文件中（或使用算术编码）。

通常，解码器是完全特定的。编码算法由其设计者自行决定，但需确保文件可以被解码。

在颜色信息的子采样、量化等操作允许的范围内，可以选择最佳的质量、位数与计算复杂度的折中方案。