从多分辨率到小波

PLAN

---

• 尺度函数（Scaling functions）
• 小波（Wavelets）
• Mallat 和 Meyer 定理的证明（Proof of the Mallat and Meyer’s theorem）

遗留问题

---

• Riesz 基没有正交性质 → 正交投影到 $P_{V_j}$ 上是不实际的。
• 如何从 Riesz 基构造一个希尔伯特基（Hilbert basis）？
• 我们希望构造一个函数序列 ${\varphi }_{j,n}$，使得

$$P_{V_j}f=\sum _{-\mathrm{\infty }}^{\mathrm{\infty }}(f,{\varphi }_{j,n}){\varphi }_{j,n}$$

尺度函数 Scaling functions

---

定理

---

设 $(V_j{)}_{j\in \mathbb{Z}}$ 是一个多分辨率，并定义一个尺度函数（scaling function） $\phi \in L^2(ℝ)$，其傅里叶变换满足：对于所有 $\omega \in ℝ$，

$$\hat{\varphi }(\omega )=\frac{\hat{\theta }(\omega )}{{(\sum _{k=-\mathrm{\infty }}^{+\mathrm{\infty }}|\hat{\theta }(\omega +2k\pi ){|}^2)}^{1/2}}$$

同时定义函数

$${\varphi }_{j,n}=\frac{1}{\sqrt{2^j}}\varphi (\cdot -\frac{2^{j}n}{2^j})$$

则，对于所有 $j\in \mathbb{Z}$，序列 $({\varphi }_{j,n}{)}_{n\in \mathbb{Z}}$ 是 $V_j$ 的一个希尔伯特基。

---

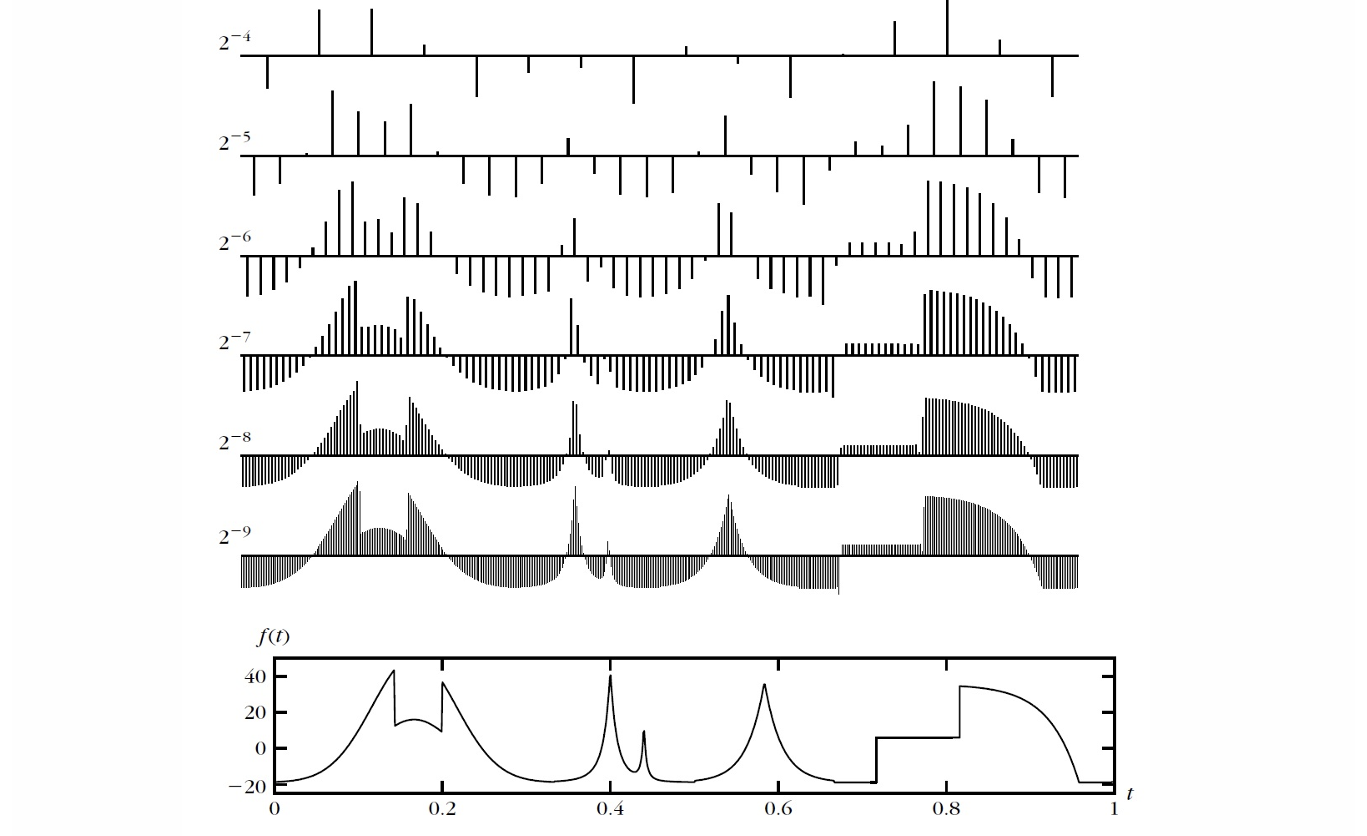
证明思路

根据多分辨率的定义，有：

$$\varphi \in V_0⟹\mathrm{\exists }{\left(a_n\right)}_{n\in \mathbb{Z}}\text{ 使得 }\varphi =\sum _{n\in \mathbb{Z}}{a}_n\theta (\cdot -n)$$

通过傅里叶变换可得：

$$\hat{\varphi }(\omega )=\hat{a}(\omega )\hat{\theta }(\omega ),\omega \in \mathbb{R},$$

其中：

$$\hat{a}(\omega )=\sum _{n\in \mathbb{Z}}{a}_n{e}^{-in\omega }$$

接下来需要在傅里叶域中表达 $(\varphi (\cdot -n){)}_{n\in \mathbb{Z}}$ 的正交性。

定义 $\tilde{\varphi }$ 使得 $\tilde{\varphi }(t)=\bar{\varphi }(-t)$。于是，对于所有 $(n,p)\in {\mathbb{Z}}^2$，有：

$$(\varphi (\cdot -n),\varphi (\cdot -p))={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (t-n)\bar{\varphi }(t-p)dt=(\varphi \ast \tilde{\varphi })(n-p).$$

因此，$(\varphi (\cdot -n){)}_{n\in \mathbb{Z}}$ 正交当且仅当：

$$(\varphi \ast \tilde{\varphi })(n)=1_{n=0}.$$

注意：$\varphi \ast \tilde{\varphi }$ 的傅里叶变换为：

$$\omega \mapsto |\hat{\varphi }(\omega ){|}^2.$$

通过采样 $\gamma =\varphi \ast \tilde{\varphi }$，得到一个分布 ${\gamma }_1$，其傅里叶变换为：

$${\hat{\gamma }}_1(\omega )=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}\hat{\gamma }(\omega -2k\pi )$$

因此，正交性等价于：

$$\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}|\hat{\varphi }(\omega +2k\pi ){|}^2=1,\omega \in \mathbb{R}.$$

这意味着我们必须选择：

$$\hat{a}(\omega )={(\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}|\hat{\theta }(\omega +2k\pi ){|}^2)}^{-1/2}.$$

示例

---

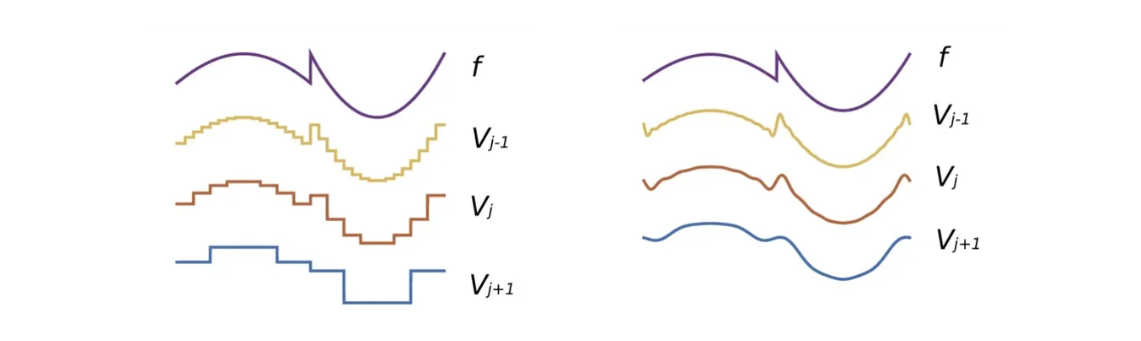
分段常数多分辨率

$\theta ={\mathbb{1}}_{[0,1[}$， 导致 Riesz 基 $(\theta (\cdot -n))n\in \mathbb{Z}$ 是正交的。

因此，$\varphi =\theta$，并且生成的函数 ${\varphi }_{j,n}$ 形成 $V_j$ 的希尔伯特基，如前所示。

Shannon 多分辨率

$\theta :t\mapsto \frac{\sin (\pi t)}{\pi t}$， 导致 $(\theta (\cdot -n){)}_{n\in \mathbb{Z}}$ 是正交 Riesz 基。

因此，设 $\varphi =\theta$。

样条多分辨率

通过卷积/乘积规则计算傅里叶变换，并应用上述定理。

---

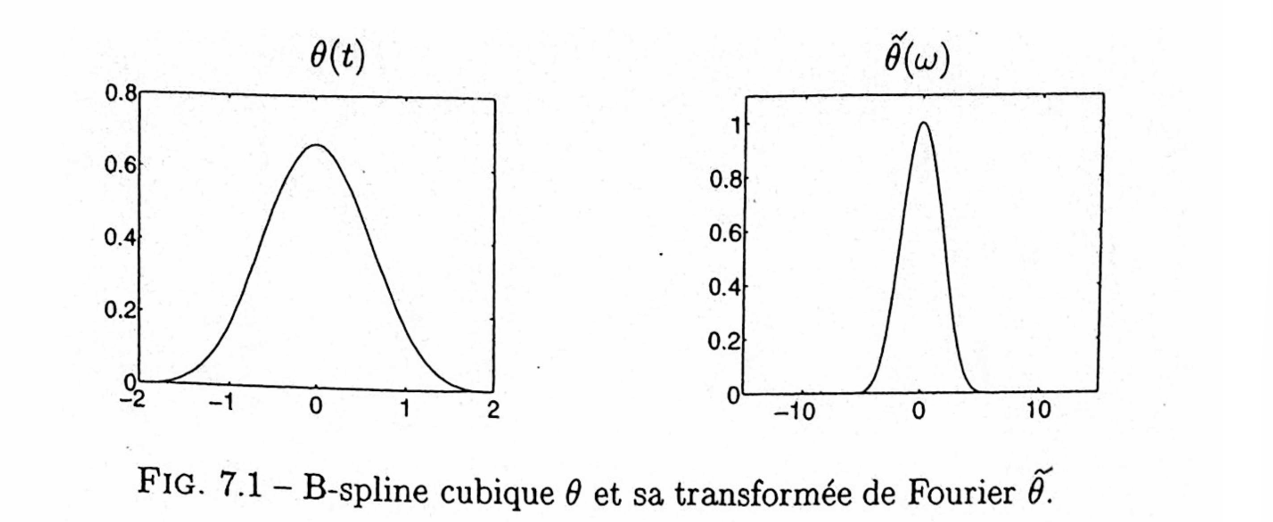
$${\tilde{\theta }}_m(\omega )={\left(\frac{\sin (\omega /2)}{\omega /2}\right)}^{m+1}\exp (-i\epsilon \frac{\omega }{2}),$$

其中：

$$\epsilon =\{\begin{array}{ll}1,& m\text{ 为偶数},\\ 0,& m\text{ 为奇数}.\end{array}$$

---

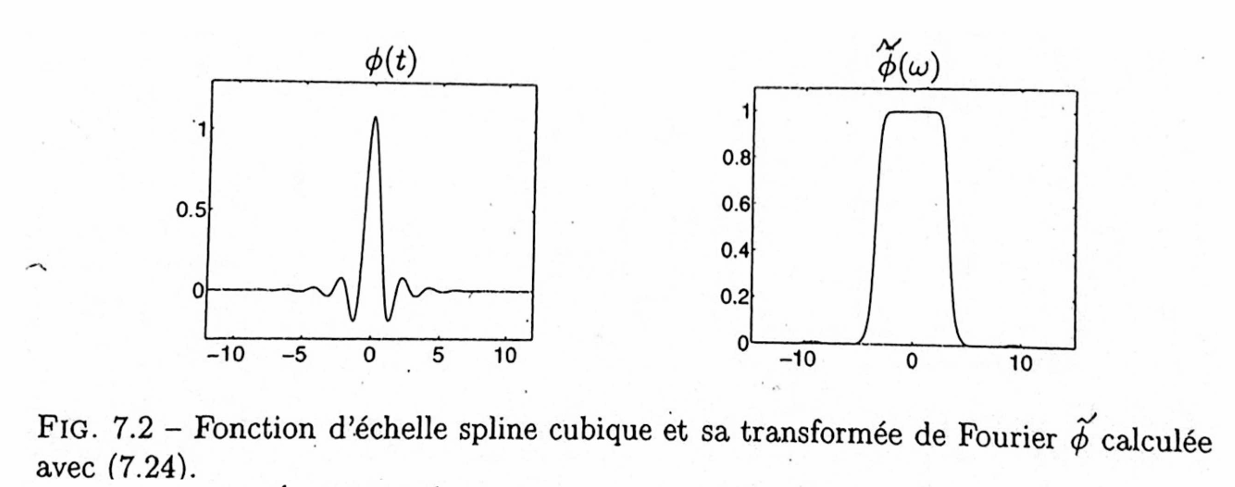
$$\hat{\varphi }(\omega )=\frac{\exp (-i\epsilon \frac{\omega }{2})}{{\omega }^{m+1}\sqrt{S_{2,m+2}(\omega )}},$$

其中：

$$S_m(\omega )=\sum _{\ell =-\mathrm{\infty }}^{\mathrm{\infty }}\frac{1}{(\omega +2\ell \pi {)}^m}.$$

具体示例：对于 $S_8(2\omega )$，有：

$$S_8(2\omega )=\frac{5+30{\cos }^2(\omega )+30{\sin }^2(\omega ){\cos }^2(\omega )}{105\cdot 2^8{\sin }^8(\omega )}+\frac{70{\cos }^4(\omega )+2{\sin }^4(\omega ){\cos }^2(\omega )+\frac{2}{3}{\sin }^6(\omega )}{105\cdot 2^8{\sin }^8(\omega )}.$$

总结

---

• 多分辨率

  多分辨率是一系列希尔伯特子空间 $(V_j{)}_{j\in \mathbb{Z}}$，用于描述在尺度 $2^j$ 下的函数。

• 子空间的特性

  每个 $V_j$ 由 $V_0$ 的一个 Riesz 基 $(\theta (\cdot -n){)}_{n\in \mathbb{Z}}$ 所表征，例如分段常数、样条等。

• 尺度函数

  通过对 $(\theta (\cdot -n)),n\in \mathbb{Z}$ 进行正交化，我们可以导出一个尺度函数 $\varphi$，它生成 $V_j$ 的希尔伯特基 $\{{\varphi }_{j,n}{\}}_{n\in \mathbb{Z}}$。这些基函数由 $\varphi$ 通过尺度和平移得到：

  $${\varphi }_{j,n}=\frac{1}{\sqrt{2^j}}\varphi (\cdot -\frac{2^{j}n}{2^j}).$$

• 多分辨率的意义

  多分辨率的概念使得我们可以在不同尺度下构建 $f$ 的近似层次结构，从而保证无信息丢失。但这对压缩有何用处？

小波 Wavelets

---

主要思想 main idea

---

对于 $j\in \mathbb{Z}$，构造一个 Hilbert 子空间 $W_{j+1}$，使得

$$V_{j+1}\oplus W_{j+1}=V_j$$

因此，对于任意 $f\in L^2(\mathbb{R})$，满足

$$P_{V_j}f=P_{V_{j+1}}f+P_{W_{j+1}}f$$

即，$P_{W_{j+1}}f$ 包含了 $f$ 在尺度 $2^j$ 存在但在尺度 $2^{j+1}$ 消失的细节信息。

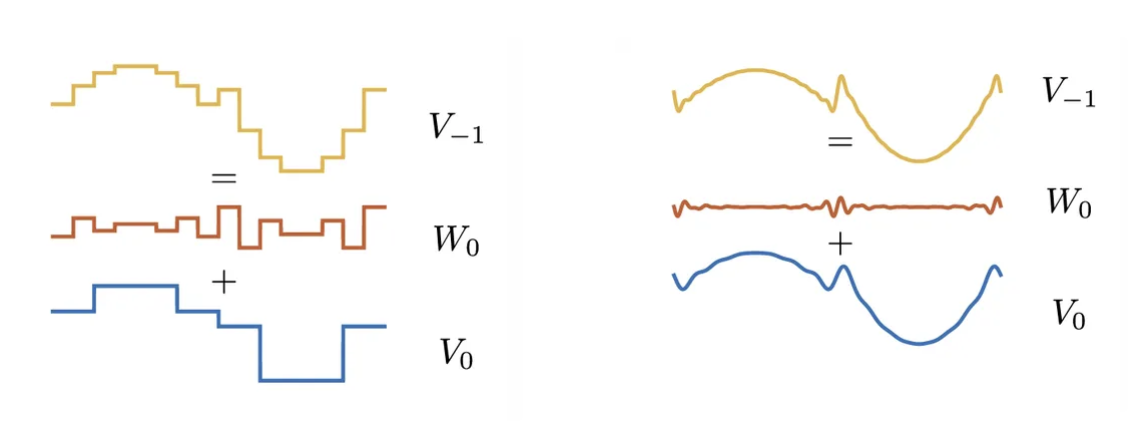
事实上，我们可以理解为：

• $P_{V_{j+1}}f$ 对应于通过低通滤波器 (low-pass filter) 对 $P_{V_j}f$ 进行滤波。
• $P_{W_{j+1}}f$ 对应于通过高通滤波器 (high-pass filter) 对 $P_{V_j}f$ 进行滤波。

共轭镜像滤波器 Conjugate Mirror Filter

---

定义

令 $\varphi \in L^2(\mathbb{R})$ 是一个尺度函数。对所有 $n\in \mathbb{Z}$，定义：

$$h_n=(\frac{1}{\sqrt{2}}\varphi (\cdot /2),\varphi (\cdot -n))$$

这些是 $\frac{1}{\sqrt{2}}\varphi (\cdot /2)$ 在 $V_1$ 上投影到 $V_0$ 的系数：

$$\frac{1}{\sqrt{2}}\varphi (\cdot /2)=\sum _n{h}_n\varphi (\cdot -n)$$

序列 $(h_n{)}_{n\in \mathbb{Z}}$ 是一个低通滤波器 (low-pass filter) 的冲激响应，称为共轭镜像滤波器 (conjugate mirror filter)。

---

注记

$$\begin{array}{}\text{(1)}& \frac{1}{\sqrt{2}}\varphi (\cdot /2)=\sum _n{h}_n\varphi (\cdot -n)⟹\sqrt{2}\hat{\varphi }(2\omega )=\hat{\varphi }(\omega )\cdot \left(\sum _n{h}_n{e}^{-in\omega }\right),\omega \in \mathbb{R}\end{array}$$

• 通过对两边取傅里叶变换，考虑傅里叶级数

  $$\hat{h}(\omega )=\sum _n{h}_n{e}^{-in\omega },\omega \in \mathbb{R}$$

• 傅里叶级数是 $2\pi$-周期的)。

• 我们可以将 $(1)$ 重写为：

$$\hat{\varphi }(2\omega )=\hat{\varphi }(\omega )\frac{\hat{h}(\omega )}{\sqrt{2}},\omega \in \mathbb{R}$$

---

示例

1. Shannon 多分辨率 (Shannon Multiresolution):

   • $\hat{\varphi }={\mathbf{1}}_{[-\pi ,\pi ]}$。
   • 因此，$\mathrm{\forall }\omega \in [-\pi ,\pi ]$：

   $${\mathbb{1}}_{[-\pi /2,\pi /2]}={\mathbb{1}}_{[-\pi ,\pi ]}\hat{h}(\omega )/\sqrt{2}$$

   • 由此可得，$\mathrm{\forall }\omega \in [-\pi ,\pi ]$：

   $$\hat{h}(\omega )=\sqrt{2}\cdot {\mathbf{1}}_{[-\pi /2,\pi /2]}(\omega ).$$

2. 分段常值多分辨率 (Piecewise Constant Multiresolution):

   • $\varphi ={\mathbf{1}}_{[0,1]}$。

   • 由

     $$h_n=(\frac{1}{\sqrt{2}}\varphi (\cdot /2),\varphi (\cdot -n)),$$

   • 得

     $$h_n=\{\begin{array}{ll}{2}^{-1/2},& \text{如果 }n=0,1,\\ 0,& \text{其他情况}.\end{array}$$

   • 这有时被称为局部平均 (local average)。

3. 样条多分辨率 (Spline Multiresolution):

   • 对于 $m$ 阶 box 样条， $\hat{\varphi }$ 的表达式

     $$\hat{\varphi }(\omega )=\frac{\exp (-i\epsilon \frac{\omega }{2})}{{\omega }^{m+1}\sqrt{S_{2,m+2}(\omega )}},$$

   • 代入$\hat{\varphi }(2\omega )=\hat{\varphi }(\omega )\frac{\hat{h}(\omega )}{\sqrt{2}},\omega \in \mathbb{R}.$

   • 得，$\mathrm{\forall }\omega \in \mathbb{R}$：

   $$\hat{h}(\omega )=\exp (-\frac{i\omega }{2})\sqrt{\frac{S_{2m+2}(\omega )}{2^{m+1}{S}_{2m+2}(2\omega )}}.$$

高通滤波器的构造

---

• 令 $\varphi \in L^2(\mathbb{R})$ 为一个尺度函数，$(h_n{)}_{n\in \mathbb{Z}}$ 为相应的共轭镜像滤波器。
• 定义一个滤波器 $(g_n{)}_{n\in \mathbb{Z}}$，其傅里叶变换满足以下条件：

$$\hat{g}(\omega )=e^{-i\omega }\hat{h}(\omega +\pi ),\mathrm{\forall }\omega \in \mathbb{R}.$$

---

注记

• 根据傅里叶变换的性质：

$$g_n=(-1{)}^{1-n}{h}_{1-n},\mathrm{\forall }n\in \mathbb{Z}.$$

• $(g_n)$ 是一个高通滤波器 (high-pass filter)，因为：

  $$|\hat{g}(\omega )|=|\hat{h}(\omega +\pi )|,$$

  且 $\hat{h}$ 是 $2\pi$-周期函数。

Mallat-Meyer定理

---

令 $\varphi \in L^2(\mathbb{R})$ 为一个尺度函数，$(g_n{)}_{n\in \mathbb{Z}}$ 为对应的滤波器（如前述定义）。考虑函数 $\psi \in L^2(\mathbb{R})$，称为小波函数 (wavelet function)，其傅里叶变换满足：

$$\hat{\psi }(2\omega )=\frac{\hat{\varphi }(\omega )\hat{g}(\omega )}{\sqrt{2}},\mathrm{\forall }\omega \in \mathbb{R}.$$

此外，对于所有 $(j,n)\in {\mathbb{Z}}^2$，定义：

$${\psi }_{j,n}(t)=\frac{1}{\sqrt{2^j}}\psi \left(\frac{t-2^{j}n}{2^j}\right).$$

则，对于任意 $j\in \mathbb{Z}$ 和对应的尺度 $s=2^j$，集合 $\{{\psi }_{j,n}{\}}_{n\in \mathbb{Z}}$ 是子空间 $W_j$ 的一个Hilbert 基。

此外，对于整体尺度范围，集合 $\{{\psi }_{j,n}{\}}_{(j,n)\in {\mathbb{Z}}^2}$ 是 $L^2(\mathbb{R})$ 的一个称为小波基 (wavelet basis) 的 Hilbert 基。

---

1. $\psi (\cdot /2)\in W_1\subset V_0$，因此存在 $(g_n)n\in \mathbb{Z}$ 使得：

   $$\frac{1}{\sqrt{2}}\psi (\cdot /2)=\sum {n=-\mathrm{\infty }}^{\mathrm{\infty }}{g}_n\varphi (\cdot -n),$$

   其中：

   $$g_n=(\frac{1}{\sqrt{2}}\psi (\cdot /2),\varphi (\cdot -n)).$$

2. 取傅里叶变换：

   $$\hat{\psi }(2\omega )=\frac{\hat{\varphi }(\omega )\hat{g}(\omega )}{\sqrt{2}},\omega \in \mathbb{R}.$$

---

示例

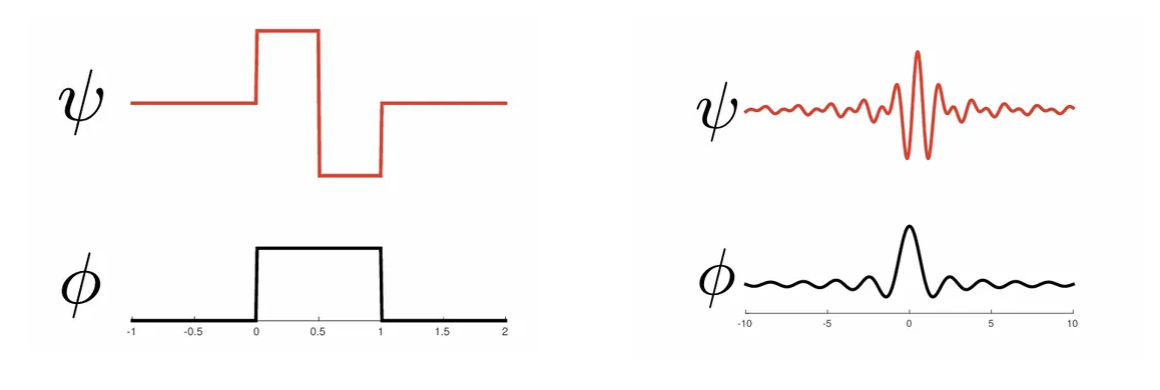
Haar 小波 (Haar Wavelets)

1. 尺度函数 (Scaling Function):

   $$\varphi ={\mathbf{1}}_{[0,1]}$$

2. 共轭镜像滤波器 (Conjugate Mirror Filter):

   $$h_n=\{\begin{array}{ll}{2}^{-1/2},& \text{if }n=0,1,\\ 0,& \text{otherwise.}\end{array}$$

3. 滤波器 $(g_n)$:

   $$g_n=\{\begin{array}{ll}-2^{-1/2},& \text{if }n=0,\\ 2^{-1/2},& \text{if }n=1,\\ 0,& \text{otherwise.}\end{array}$$

4. 小波函数 (Wavelet):

   $$\psi (t)=\{\begin{array}{ll}-1,& \text{if }0\le t<1/2,\\ 1,& \text{if }1/2\le t<1,\\ 0,& \text{otherwise.}\end{array}$$

Shannon 小波 (Shannon Wavelets)

1. 尺度函数 (Scaling Function):

   $$\varphi (t)=\frac{\sin (\pi t)}{\pi t}$$

2. 共轭镜像滤波器 (Conjugate Mirror Filter):

   $$\hat{h}(\omega )=\sqrt{2}\cdot {\mathbf{1}}_{[-\pi /2,\pi /2]}(\omega )$$

3. 滤波器 $(g_n)$:

   $$\hat{g}(\omega )=\{\begin{array}{ll}{e}^{-i\omega /2},& \text{if }\omega \in [-2\pi ,\pi ]\cup [\pi ,2\pi ],\\ 0,& \text{otherwise.}\end{array}$$

4. 小波函数 (Wavelet):

   $$\psi (t)=\frac{\sin (2\pi (t-1/2))}{\pi (t-1/2)}-\frac{\sin (\pi (t-1/2))}{\pi (t-1/2)}.$$

Battle-Lemarié / Cubic Spline 小波

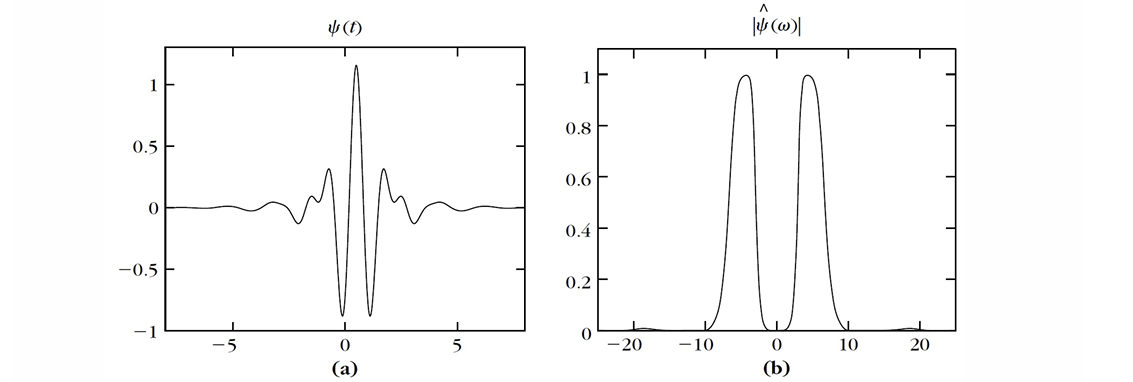
$L^2(\mathbb{R})$ 的分解

---

Parseval 等式: 对于 $f\in L^2(\mathbb{R})$，

$$f=\sum _{j\in \mathbb{Z}}{P}_{W_j}f=\sum _j\sum _n⟨f,{\psi }_{j,n}⟩{\psi }_{j,n}.$$

$f$ 是通过不同尺度的子空间 $W_j$ 分解成多个分量的和。

---

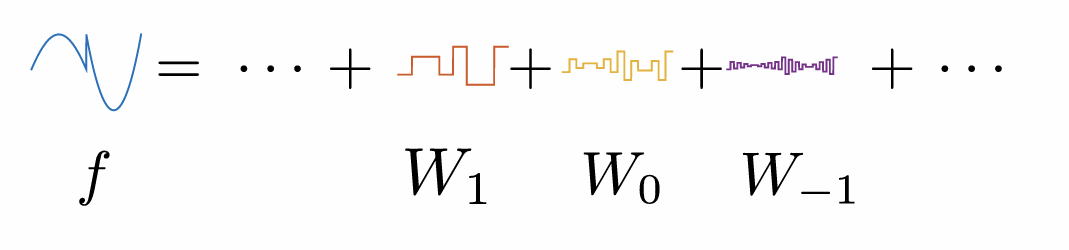
另一种 Hilbert 空间分解

• Hilbert 空间的表达:

  $$L^2(\mathbb{R})=V_J\oplus \underset{j=J}{\overset{\mathrm{\infty }}{⨁}}{W}_j,$$

  其中 $J$ 是某个粗略尺度。

• 对于任意 $f\in L^2(\mathbb{R})$，

  $$\begin{array}{rl}f& =P_{V_J}f+\sum _{j=-\mathrm{\infty }}^J{P}_{W_j}f\\ & =\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}(f,{\varphi }_{J,n}){\varphi }_{J,n}+\sum _{j=-\mathrm{\infty }}^J\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}(f,{\psi }_{j,n}){\psi }_{j,n}\end{array}$$

Mallat-Meyer定理的证明

---

定理1

对于共轭镜像滤波器 $(h_n{)}_{n\in \mathbb{Z}}$，其傅里叶变换（傅里叶级数形式）表示为：

$$\hat{h}(\omega )=\sum n{h}_n{e}^{-in\omega },\omega \in \mathbb{R},$$

满足以下性质：

1. 对于任意 $\omega \in \mathbb{R}$：

   $$|\hat{h}(\omega ){|}^2+|\hat{h}(\omega +\pi ){|}^2=2.$$

2. $\hat{h}(0)=\sqrt{2}.$

---

定理 2

反之，令 $\hat{h}$ 是一个 $2\pi$-周期函数，并满足以下条件：

1. $\hat{h}\in C^1$ 在零点邻域中连续可导；

2. 在 $\omega \in [-2\pi ,2\pi ]$ 内有 $inf|\hat{h}(\omega )|>0$；

3. 对于任意 $\omega \in \mathbb{R}$：

   $$|\hat{h}(\omega ){|}^2+|\hat{h}(\omega +\pi ){|}^2=2;$$

4. $\hat{h}(0)=\sqrt{2}.$

则傅里叶变换为

$$\hat{\varphi }(\omega )=\prod _{j=1}^{\mathrm{\infty }}\frac{\hat{h}(2^{-j}\omega )}{\sqrt{2}},\omega \in \mathbb{R},$$

的函数 $\varphi \in L^2(\mathbb{R})$ 是一个尺度函数。

---

证明

• 假设 $(h_n)$ 是一个共轭镜像滤波器：

  $$\hat{\varphi }(2\omega )=\frac{\hat{\varphi }(\omega )\hat{h}(\omega )}{\sqrt{2}},\omega \in \mathbb{R}.$$

• 对任意 $p\in \mathbb{Z}$，有：

$$\hat{\varphi }(2^{p+1}\omega )=\frac{\hat{\varphi }(2^p\omega )\hat{h}(2^p\omega )}{\sqrt{2}}.$$

• 反复迭代，得到

$$\hat{\varphi }(\omega )=\prod _{p=1}^K\frac{\hat{h}(2^{-p}\omega )}{\sqrt{2}}\cdot \hat{\varphi }(2^{-K}\omega ).$$

• 当 $K\to \mathrm{\infty }$ 时，$\hat{\varphi }(2^{-K}\omega )\to 1$，因此：

$$\hat{\varphi }(\omega )=\prod _{p=1}^{\mathrm{\infty }}\frac{\hat{h}(2^{-p}\omega )}{\sqrt{2}}.$$

---

Hilbert 基的正交归一性

• 归一性关系

$$\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}|\hat{\varphi }(\omega +2k\pi ){|}^2=1,\omega \in \mathbb{R}.$$

• 该公式表达了 $(\varphi (\cdot -n){)}_{n\in \mathbb{Z}}$ 的 Hilbert 基正交归一性。

• 带入 $\hat{\varphi }(2\omega )=\frac{\hat{\varphi }(\omega )\hat{h}(\omega )}{\sqrt{2}}$:

  $$\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}{\left|\hat{h}(\frac{\omega }{2}+k\pi )\right|}^2\cdot {\left|\hat{\varphi }(\frac{\omega }{2}+k\pi )\right|}^2=2.$$

• 使用 $k=2p$ 或 $k=2p+1$ 进行拆分，重新排列得到：

$${\left|\hat{h}\left(\frac{\omega }{2}\right)\right|}^2\sum _{p=-\mathrm{\infty }}^{\mathrm{\infty }}{\left|\hat{\varphi }(\frac{\omega }{2}+2p\pi )\right|}^2+{\left|\hat{h}(\frac{\omega }{2}+\pi )\right|}^2\sum _{p=-\mathrm{\infty }}^{\mathrm{\infty }}{\left|\hat{\varphi }(\frac{\omega }{2}+(2p+1)\pi )\right|}^2=2.$$

• 再次带入

  对 ${\omega }^{\prime }=\frac{\omega }{2}$ 或 ${\omega }^{\prime }=\frac{\omega }{2}+\pi$，最终得到：

  $$|\hat{h}({\omega }^{\prime }){|}^2+|\hat{h}({\omega }^{\prime }+\pi ){|}^2=2.$$

---

• 结论 $|\hat{h}(\omega ){|}^2+|\hat{h}(\omega +\pi ){|}^2=2$ 是 $(\varphi (\cdot -n){)}_{n\in \mathbb{Z}}$ 成为 Hilbert 基的必要条件。
• 它对应于正交归一要求，保证尺度函数 $\varphi$ 的构造正确。

---

Hilbert 基的构造

为了证明 $(\psi (\cdot -n){)}_{n\in \mathbb{Z}}$ 是 $W_0$ 的 Hilbert 基，需要使用以下引理。

引理

• 序列 $({\psi }_{j,n}{)}_{n\in \mathbb{Z}}$ 是 $W_j$ 的 Hilbert 基，当且仅当以下两个条件成立：

  1. $\hat{g}(\omega )$ 满足归一性：

     $$|\hat{g}(\omega ){|}^2+|\hat{g}(\omega +\pi ){|}^2=2.$$

  2. $\hat{g}(\omega )$ 与 $\hat{h}(\omega )$ 的正交性条件：

     $$\hat{g}(\omega ){\hat{h}}^{\ast }(\omega )+\hat{g}(\omega +\pi ){\hat{h}}^{\ast }(\omega +\pi )=0$$

• 解释：
  • 条件 (i) 对应于 $(\psi (\cdot -n){)}_{n\in \mathbb{Z}}$ 的正交归一性。
  • 条件 (ii) 保证 $W_0$ 与 $V_0$ 正交，即 $(\psi ,\varphi (\cdot -n))=0$ 对于所有 $n\in \mathbb{Z}$。

---