基于线性预测的编码
基于线性预测的编码
编码是存储或者传输语音信号,同时保证其可理解性的一种方式。在电话通信,语音合成中都有应用。 基于线性预测的语音编码是以语音物理生成模型为基础的。这些是从模型中估计出的参数,它们被传输、存储,然后用于重建。这种重建并不是为了重新合成与输入信号非常接近的信号,而是为了生成一个具有与原始信号相似统计属性(尤其是功率谱密度)的信号。这种方法足以让编码在感知上保持真实。
PLAN
- 语音研究(信号,音系学 phonologique,语义学 sémantique)
- 构建参数化模型
- 参数估计
- 实现细节
- 限制与扩展
- 应用
语音生成模型
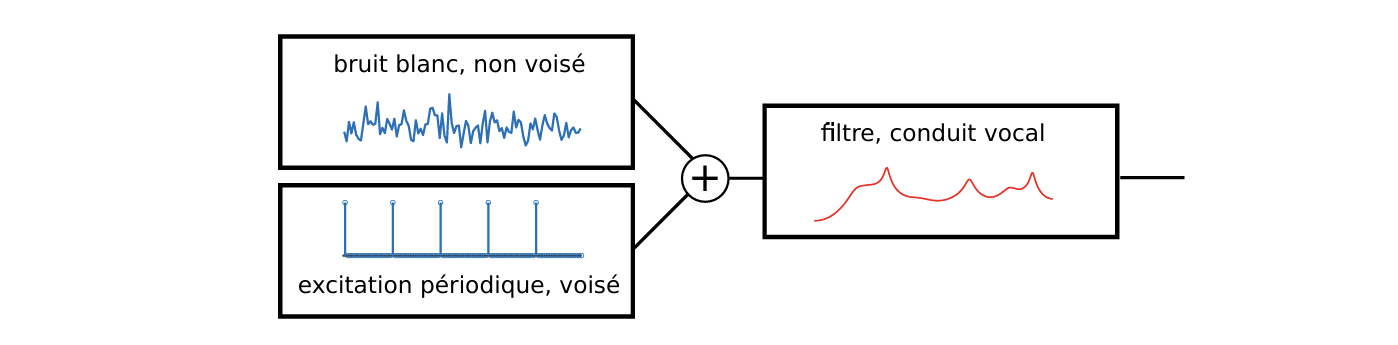
语音的生成可以建模为:
- 一个源,产生一个通常是周期性或随机的信号;有声的声音对应于周期性情况,无声的声音则对应于随机情况。
- 一个滤波器,作用于该信号。
常见的声源是气流通过声带的运动(频率周期性的开合产生的声音,或者如果声带接近但未闭合则会产生随机湍流),以及由于气流通过声道狭窄区域(例如舌头和上颚、牙齿之间、舌头等)而产生的湍流。
滤波器是通过声道(嘴、鼻等)的传播,这种传播形式是可变的。
模型及参数估计
我们优先关注无声的情况,可以很好地用随机过程建模。目标是估计和表示过程的功率谱密度。
通常基于自回归(Auto-Regressive, AR)模型,其中过程\(X\) 由其阶数\(p\)、系数\(a_p\) 和以下公式定义:
\[ X[n]=W[n]+\sum_{p=1}^P a_p X[n-p] \]
其中\(W[n]\)是方差为\(\sigma^2\)的白噪音,且独立于\(X[k]\)。
考虑如何从\(W[n]\)得到\(X[n]\),变换公式得到:
\[ X[n]-\sum_{p=1}^P a_p X[n-p] = X[n]*[1,-a_1,-a_2,...,-a_p]=W[n] \]
等价于:
\[ A(z) \cdot X(z)=E(z) \]
由此,可得传递函数:
\[ H(z)=\frac{X(z)}{E(z)}=\frac{1}{A(z)} \]
为了得到这个结果,可以通过如下python代码实现。其中si.lfilter的前两个参数代表传递函数的分子和分母,后一个参数代表原始信号。
1 | A = np.concatenate(([1], -a)) |
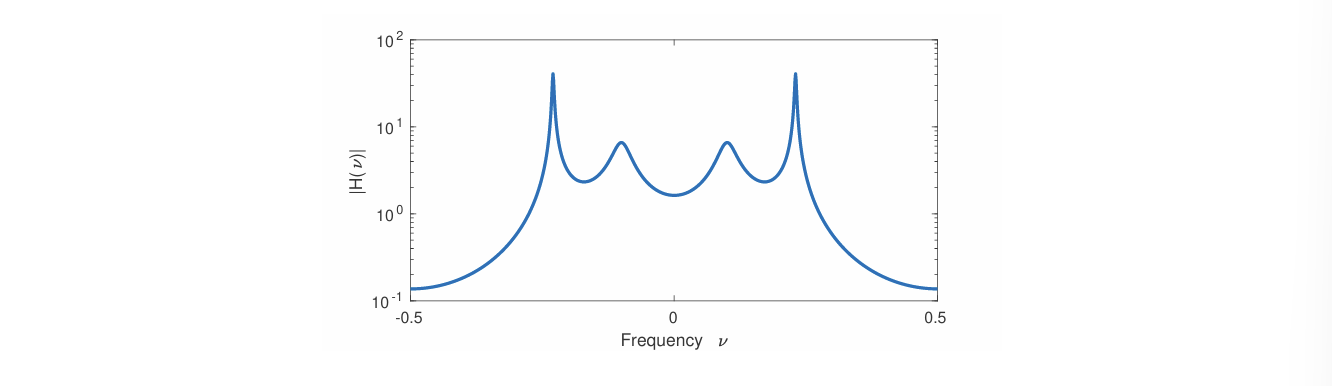
使用此模型的理由是其能够创建共振峰(formants),这些共振峰对应于声道的谐振频率强度带。
上图显示了由以下 AR 过程定义的功率谱密度(DSP):
\[ X[n]=1.70 X[n-1]-2.15 X[n-2]-1.62 X[n-3]+0.79 X[n-4]+W[n] . \]
该模型的传递函数的极点为 \(0.9 e^{i 2 \pi \times( \pm 0.1)}\) 和 \(0.99 e^{i 2 \pi \times( \pm 0.23)}\) ,分别表示为峰值的中心频率(相位)及其宽度(模值)。
参数估计
我们选择矩估计法(méthode des moments)来进行参数估计:寻找参数与随机模型矩(此处为自相关)的关系,然后通过求解该关系,并使用这些矩的估计值进行参数反演。
计算\(E(X[n]X[n-k])\),对于\(k\ge1\):
\[ \begin{aligned}\mathbf{E}(X[n] X[n-k]) & =\mathbf{E}\left(\left(\sum_{p=1}^P a_p X[n-p]+W[n]\right) X[n-k]\right) \\& =\sum_{p=1}^P a_p \gamma_{X X}[k-p] \\& =\gamma_{X X}[k]\end{aligned} \]
同时对于\(k = 0\):
\[ \mathbf{E}\left(X[n]^2\right)=\gamma_{X X}[0]=\sum_{p=1}^P a_p \gamma_{X X}[p]+\sigma^2 \]
因此,对于\(1\le k \le P\),\(a_p\)的解可以通过Yule-Walker方程组获得:
\[ \left(\begin{array}{cccc}\gamma_{X X}[0] & \gamma_{X X}[1] & \cdots & \gamma_{X X}[P-1] \\\gamma_{X X}[1] & \gamma_{X X}[0] & \cdots & \gamma_{X X}[P-2] \\\vdots & \vdots & \ddots & \vdots \\\gamma_{X X}[P-1] & \gamma_{X X}[P-2] & \cdots & \gamma_{X X}[0]\end{array}\right)\left(\begin{array}{c}a_1 \\a_2 \\\vdots \\a_P\end{array}\right)=\left(\begin{array}{c}\gamma_{X X}[1] \\\gamma_{X X}[2] \\\vdots \\\gamma_{X X}[P]\end{array}\right) \]
通过构建该系统并使用自相关估计值 \(\hat{\gamma}_{X X}\) 求解,参数 \(\hat{a}_p\) **被估计出来。 模型阶数可以通过检验信号估计 \(\hat{W}[n]=X[n]-\sum_{p=1}^P \hat{a}_p X[n-p]\) 来估计,其应当(近似)为白噪声,前提是阶数足够大。
\(\gamma_{XX}=\frac{1}{N} \sum_{n=0}^{N-1} X[n] \cdot X[n-k], \quad k=-(N-1), \ldots, N-1\)是信号\(X\)的自相关。全部的计算在python中可以如下实现。
1 | r = np.correlate(X, X, mode='full') / len(X) |

