Transformer01 gpt模型的原理与实现

从RNN到Transformer

---

2017年，谷歌的研究人员发表了一篇论文，提出了一种用于序列建模的新型神经网络架构，称为Transformer。这种架构在机器翻译任务中，在翻译质量和训练成本方面都优于循环神经网络（RNN）。

与此同时，一种名为ULMFiT的有效迁移学习方法展示了在一个非常大且多样的语料库上训练长短期记忆（LSTM）网络，能够在仅有少量标注数据的情况下生成最先进的文本分类器。

这些进展成为了当今两个最著名的Transformer模型的催化剂：生成式预训练Transformer（GPT）和双向编码器表示Transformer（BERT）。通过将Transformer架构与无监督学习相结合，这些模型消除了从头开始训练特定任务架构的需求，并在几乎所有的自然语言处理基准

Transformer的诞生依赖于三项技术的先后开创：

• 编码器-解码器架构
• 注意力机制
• 迁移学习

编码器-解码器架构 Encoder-Decoder Framework

---

编码器-解码器架构早在循环神经网络中iu已经得到广泛应用。循环神经网络是一种“有记忆的”网络。具体的内容和实现方式可以参照之前的生成式神经网络笔记的相应部分。简单来说，这是一种满足\(y_i = f(x_i,y_{i-1})\)的神经网络结构，最终的输出\(y_t\)理论上能包含所有输入的信息，称为最后的隐藏状态。

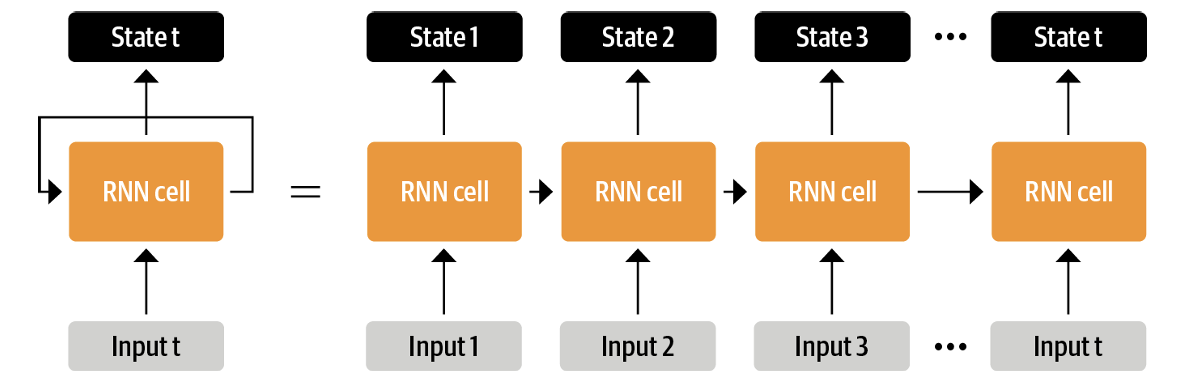
这个过程将输入信息转化为一个向量，可以将其称之为编码。

用相同的方式，将包含所有信息的最后的隐藏状态进行逐步解码，即可实现如翻译等自然语言处理任务。

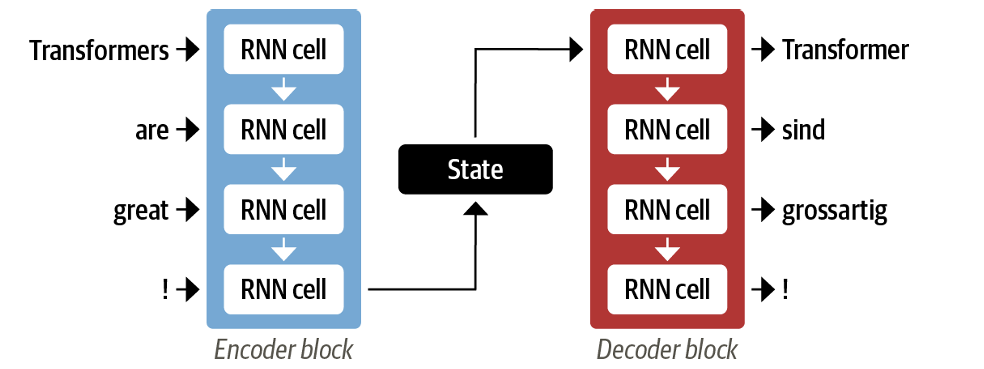
但是，在这样的做法中，由于只有最终隐藏状态被解码器获值，可能会造成部分内容在压缩过程中的丢失。

注意力机制

---

注意力机制是解决上述问题的一个“显而易见的方法”。其核心思想是，将编码器每一步生成的状态都作为输入给予解码器，并为每一个状态赋予相应的权重。

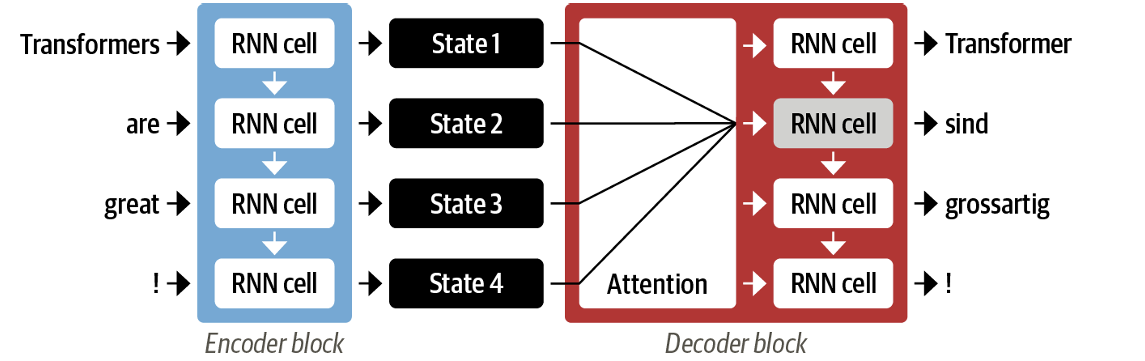
如此训练的注意力模型应该可以理解输入与生成的复杂对应关系，比如一个翻译方面的例子：

一个合格的注意力块正确的给认识了法语和英语在形容词位置上的差异。但是，我们可能会注意到这样做的一种不合理之处：例如对于State 4，注意力衡量的并非！的对结果的影响大小，而是前四个单词提供的所有信息的影响。这显然会造成每一个state中包含的信息是不平等的。同时，计算本质上是顺序进行的，无法在输入序列上并行化处理。

Transformer引入了一种新的建模范式：完全放弃循环结构，转而完全依赖一种特殊形式的注意力机制，称为自注意力机制。在这里我们先不详细涉及这种机制的具体实现，首先关注其原理。

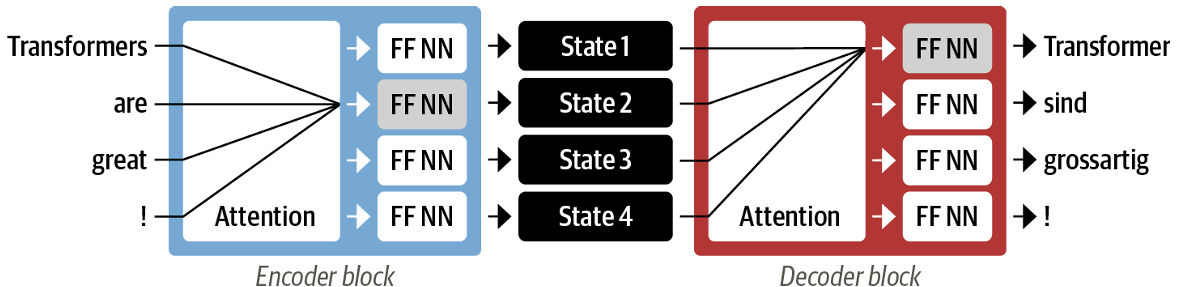
上图展现了这种模型的工作原理。首先，编码器注意力头会将输入信息转化为多个状态，每个状态都是平等的，他们拥有对输入的不同权重分配和一个线性神经网络用于进一步的处理。然后，解码器再根据不同的任务（如对单词Transformer的翻译）决定不同状态的权重，并再次经过线性神经网络得到输出。

迁移学习 Transfer Learning

---

迁移学习原理十分简单，即训练一个极其泛化的模型，然后为使用这个模型进行进一步的后续任务。

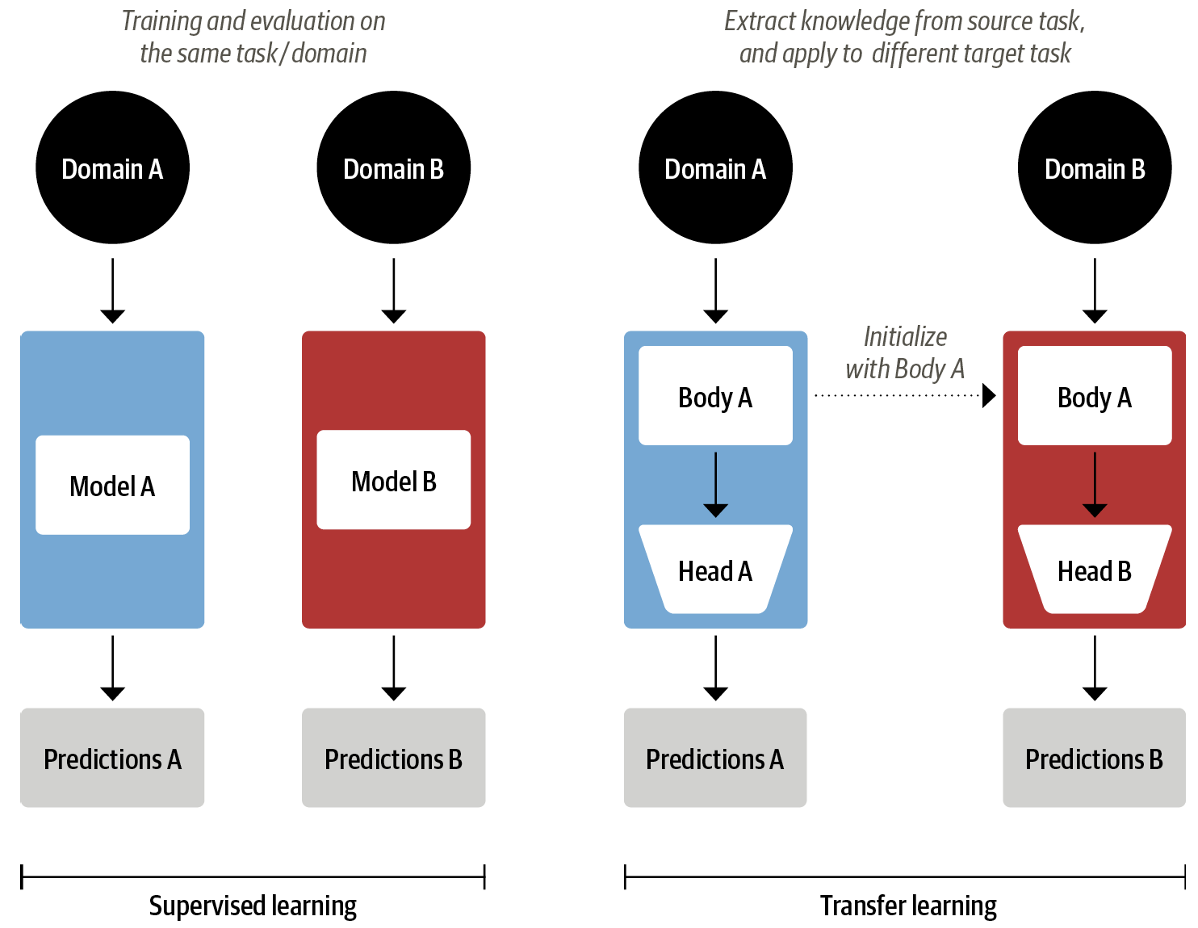
具体来说，在早期的迁移学习模型c中，作者提出通用的迁移学习狂降，将训练大致分为三个部分：

• 预训练 Pretraining：对于ULMFiT，预训练进行根据前面的词预测下一个词的简单任务，称之为语言建模。在这个过程中进行无监督训练。
• 领域适应 Domain adaption：将预训练完成的模型适用于领域内的语料库，依然使用语言建模。实际上对于较小的任务，这一步可能并非必要的。
• 微调 Fine-tuning：通过监督学习，为语言模型增加一个任务层，以实行目标任务。

数据

---

字符编码 token encoding

---

相比于图像，文本并非由连续的数值表示。计算机显然不能直接识别字母，因此需要进行分词Tokenization。分词是将字符串拆解成模型使用的基本单位的步骤。另外，关于编码encoding，嵌入embedding ，本文认为：

• Encoding 是一种更通用的表示，用于将输入数据转换为适合模型处理的某种内部表示。这种表示可能是稠密的或稀疏的，低维或高维的。Encoding可以包括Embedding 。
• Embedding 是特定的编码方法，主要用于将离散的输入映射为低维稠密向量，目的是生成一种可训练的向量表示。

字符分词

---

字符分词是最简单的分词方式。这种方法将一句话分为由单个字符组成的数组，如对于输入"Tokenizing text is a core task of NLP." ，分词后的结果是：

text = "Tokenizing text is a core task of NLP."
tokenized_text = list(text)
---`
['T', 'o', 'k', 'e', 'n', 'i', 'z', 'i', 'n', 'g', ' ', 't', 'e', 'x', 't', ' ', 'i', 's', ' ', 'a', ' ', 'c', 'o', 'r', 'e', ' ', 't', 'a', 's', 'k', ' ', 'o', 'f', ' ', 'N', 'L', 'P', '.']`

然后为每一个字符分配一个唯一的整数。如：

token2idx = {ch: idx for idx, ch in enumerate(sorted(set(tokenized_text)))}
---
{' ': 0, '.': 1, 'L': 2, 'N': 3, 'P': 4, 'T': 5, 'a': 6, 'c': 7, 'e': 8, 'f': 9, 'g': 10, 'i': 11, 'k': 12, 'n': 13, 'o': 14, 'r': 15, 's': 16, 't': 17, 'x': 18, 'z': 19}

如此，输入转化为：

input_ids = [token2idx[token] for token in tokenized_text]
---
[5, 14, 12, 8, 13, 11, 19, 11, 13, 10, 0, 17, 8, 18, 17, 0, 11, 16, 0, 6, 0, 7, 14, 15, 8, 0, 17, 6, 16, 12, 0, 14, 9, 0, 3, 2, 4, 1]

然后，可以将输入转化为独热向量one-hot vectors ，这种表示方法中，每一个与字符集大小等长的向量代表一个字符，而向量中只有字符对应的整数为1，其余为0：

import torch
import torch.nn.functional as F
input_ids = torch.tensor(input_ids)
one_hot_encodings = F.one_hot(input_ids, num_classes=len(token2idx))

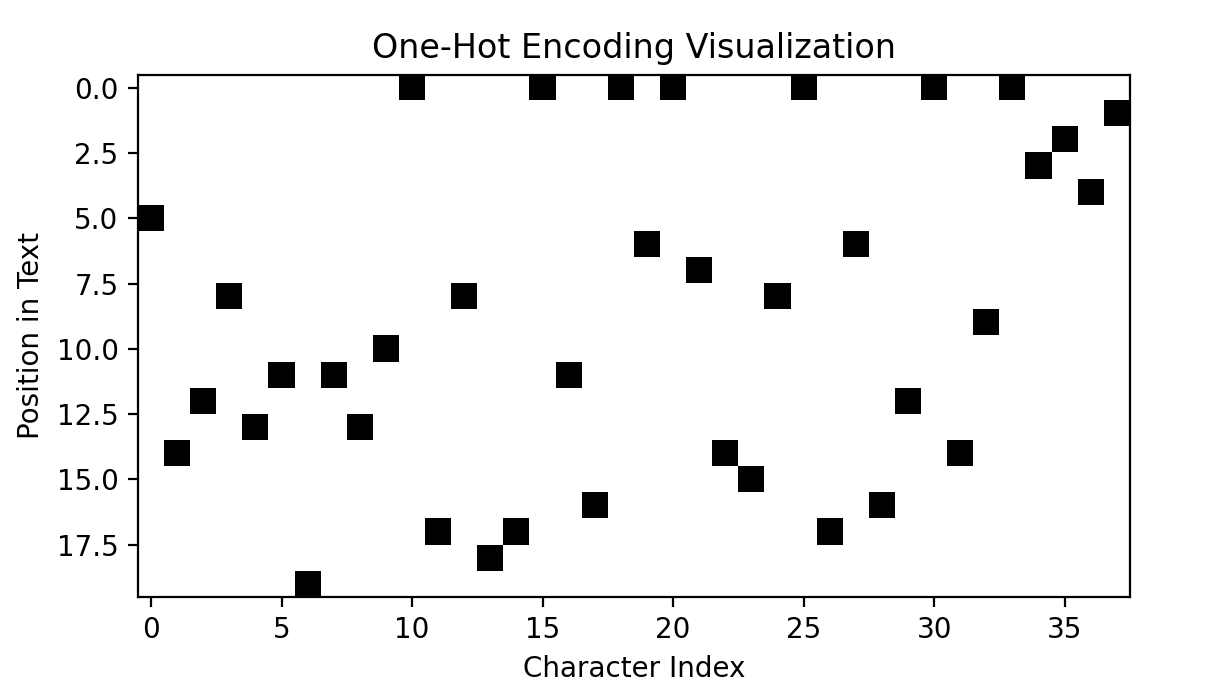
字符分词忽略了文本中的任何结构，把整个字符串视为字符流。虽然这对处理拼写错误和稀有词有帮助，但主要缺点是需要从数据中学习像词这样的语言结构。这需要大量的计算资源、内存和数据，因此字符分词在实践中很少使用。相反，在分词过程中保留一些文本结构是更常见的做法。

另外，对于中文语料，字符分词会更加常见一点。一方面中文中的字本身就是类似词的语言结构；另一方面，对中文的单词分词过于困难。

单词分词

---

顾名思义，单词分词简单的方法就是使用空格来分割文本。

tokenized_text = text.split()
---
['Tokenizing', 'text', 'is', 'a', 'core', 'task', 'of', 'NLP'，'.']

然后，像字符分词一样，将每个单词映射到一个唯一的ID。这样做有许多潜在问题：

• 显而易见的，词汇表大小很容易极其庞大
• 在分词时，'.' 被认为与单词等价，一些词级分词器会对标点符号有额外的规则处理。
• 单词可能由各种变形，可能需要应用词干提取或词形还原，将单词归一化为词干（例如，“great”、“greater”和“greatest”都会变成“great”）

关于大词汇表，有两种常见的解决方案：

• 假设我们有100万个唯一单词，我们会在神经网络的第一层将这100万维的输入向量压缩为1000维向量。这是大多数NLP架构中的标准步骤，这一层的权重矩阵大小将是100万 × 1000 = 10亿个权重。但这种方法依然过于浪费参数。
• 另一个常见的做法是限制词汇表的大小，例如只考虑语料库中最常见的10万个单词。词汇表之外的单词被分类为“未知”并映射到一个共享的UNK（未知）token。但会导致部分信息的丢失。

---

子词分词

子词分词的核心思想是将常见的高频词保持完整，而低频词或复杂单词被拆分为多个子词。NLP中常用的几种子词分词算法包括WordPiece、Byte Pair Encoding（BPE）等，这里以前者为例。

from transformers import AutoTokenizer
model_ckpt = "distilbert-base-uncased"
tokenizer = AutoTokenizer.from_pretrained(model_ckpt)
encoded_text = tokenizer(text)
okens = tokenizer.convert_ids_to_tokens(encoded_text.input_ids)
---
 ['[CLS]', 'token', '##izing', 'text', 'is', 'a', 'core', 'task', 'of', 'nl',
 '##p', '.', '[SEP]']

观察上述例子，可见：

• 在序列的开头和结尾分别添加了特殊的[CLS]和[SEP] token，用于指示序列的开始和结束。
• 每个token都被转为了小写，这是这个具体模型检查点的一个特性。
• 像“tokenizing”和“NLP”这样的单词被拆分成了两个token，这是因为它们不是常见词汇。子词前缀##表明该token不是以空格开头，表示它需要与前面的token合并回字符串。

代码实现：数据库

---

为了避免可能的错误，在本章中使用原书使用的红酒评论数据库。在后续的笔记中可能会尝试使用更多其他的数据库。

Wine Reviews

Dataset

---

本笔记的重点不在于编程，所以代码部分会简略。代码如下：

• WineDataset

  import json
  import re
  import string
  import torch
  from torch.utils.data import Dataset, DataLoader
  from collections import Counter
  from torchtext.vocab import vocab
  import torch.nn as nn
  from nltk.stem import WordNetLemmatizer
  
  class WineDataset(Dataset):
      def __init__(self, data_path, max_len, min_freq=100):
          self.data_path = data_path
          self.filtered_data = None
          self.vocab = None
          self.max_len = max_len
          self.min_freq = min_freq
          self.load_data()
          self.filter_data()
          self.data_preprocessing()
          self.transforme()
  
      def __len__(self):
          return len(self.filtered_data)
  
      def __getitem__(self, idx):
          input_ids = self.tokens[idx]
          target = self.targets[idx]
          return input_ids, target
  
      def transforme(self):
          self.tokens = []
          self.targets = []
          for text in self.filtered_data:
              tokens = (
                  [self.vocab["<bos>"]]
                  + [self.vocab[token] for token in text]
                  + [self.vocab["<eos>"]]
              )
              tokens = tokens[: self.max_len]
              tokens += [self.vocab["<pad>"]] * (self.max_len - len(tokens))
              input_ids = torch.tensor(tokens[:-1])
              target = torch.tensor(tokens[1:])
              self.tokens.append(input_ids)
              self.targets.append(target)
  
      def load_data(self):
          with open(self.data_path, encoding='UTF-8') as f:
              data = json.load(f)
          self.data = data
  
      def filter_data(self):
          '''
          确保 country（国家）、province（省份）、variety（葡萄品种）以及 description（描述）字段都不为空
          '''
          self.filtered_data = [
              "wine review : "
              + x["country"]
              + " : "
              + x["province"]
              + " : "
              + x["variety"]
              + " : "
              + x["description"]
              for x in self.data
              if x["country"] is not None
              and x["province"] is not None
              and x["variety"] is not None
              and x["description"] is not None
          ]
          n_wines = len(self.filtered_data)
          examples = self.filtered_data[25]
          print(f"{n_wines} recipes loaded, e.g. {examples}")
  
      def pad_punctuation(self, text):
          '''
          用空格替换标点符号
          '''
          s = re.sub(f"[{re.escape(string.punctuation)}]", " ", text)
          s = re.sub(" +", " ", s)
          return s
  
      def data_preprocessing(self):
          '''
          对数据进行预处理
          '''
          self.filtered_data = [
              self.pad_punctuation(x).lower() for x in self.filtered_data
          ]
          self.filtered_data = [x.split() for x in self.filtered_data]
          # wnl = WordNetLemmatizer()
          # self.filtered_data = [[wnl.lemmatize(word) for word in x] for x in self.filtered_data]
  
          # 创建词汇表，将词转换为词频
          counter = Counter()
          for x in self.filtered_data:
              counter.update(x)
  
          # 手动将特殊标记加入 Counter
          special_tokens = ["<unk>", "<pad>", "<bos>", "<eos>"]
          for token in special_tokens:
              counter[token] = float(
                  'inf'
              )  # 确保这些特殊标记有最高的频率，从而排在词表最前面
  
          # 创建词汇表, 创建四种特殊标记，分别是代表未知词的<unk>，填充标记<pad>，序列开始标记<bos>，序列结束标记<eos>
          self.vocab = vocab(
              counter,
              min_freq=self.min_freq,
              specials=["<unk>", "<pad>", "<bos>", "<eos>"],
          )
          # 设置默认索引为未知词索引
          self.vocab.set_default_index(self.vocab["<unk>"])

具体来说，我定义了WineDataset类，这是一个继承自torch.utils.data.Dataset类的子类。除了Dataset要求的__len__和__getitem__之外，该类使用load_data从json文件中读取数据；使用filter_data筛选可靠的数据；使用data_preprocessing函数删除标点和多余的空格，并使用Counter类创建词汇频次表，使用torchtext.vocab的vocab函数创建词汇表【这里注意，使用的是函数vocab而不是类Vocab，尽管前者的返回值是Vocab类】，并设置特殊标记；最后使用transfome函数完成从句子向向量的转变。

最终的结果将类似下面给出的例子，这里展示了两组输入输出。可以看到每组输入都以2：<bos>开始，都以3：<eos>结束，所有的向量都由1：<pad>补充到了举例时设置的最大长度100：

• 编码的结果

  Inputs: tensor([[   2,    4,    5,   66,  636,   89,   36,    4,   37,   40,  670,  528,
             41,   37,  834,   78,    0, 1803,  194, 2145,   19,   11,  839,   99,
             73, 1122,   16,    0,   19,   72,   48,  518,   16, 1780,  497,   55,
            563,  593,   73, 1557,  157,  642,    0,  179,  194, 1189,  956,   55,
            882,  602,  883,    3,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1],
          [   2,    4,    5,  170,  659,  659,   10,   64,  194, 1093,  145,    0,
             36,  415,    0,    0,  533,   64,   40,  273,   73,    0,   36, 2215,
              4,   37,  169,   51,   40,   82,  444,   16,  376,   31,  679,   16,
            149,   73,    9,   14,  258,   19,  108,   55,   56,  353,  105,  197,
              3,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1]])
  Targets: tensor([[   4,    5,   66,  636,   89,   36,    4,   37,   40,  670,  528,   41,
             37,  834,   78,    0, 1803,  194, 2145,   19,   11,  839,   99,   73,
           1122,   16,    0,   19,   72,   48,  518,   16, 1780,  497,   55,  563,
            593,   73, 1557,  157,  642,    0,  179,  194, 1189,  956,   55,  882,
            602,  883,    3,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1],
          [   4,    5,  170,  659,  659,   10,   64,  194, 1093,  145,    0,   36,
            415,    0,    0,  533,   64,   40,  273,   73,    0,   36, 2215,    4,
             37,  169,   51,   40,   82,  444,   16,  376,   31,  679,   16,  149,
             73,    9,   14,  258,   19,  108,   55,   56,  353,  105,  197,    3,
  				    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,    1,
              1,    1,    1]])

此外，如以下例子，直接应用词汇表将被映射为第二行的数字，brimstone 一词被映射为0：<unk>，这是因为在常见词汇表时设置了最低频率为100 ，这将有效减少词汇表。事实上，当min_freq设置为1时，词汇表大小为35972；当min_freq设置为10时，词大小为9390；设置为100时将减少到3041。

['wine', 'review', 'italy', 'sicily', 'sardinia', 'white', 'blend', 'aromas', 'include', 'tropical', 'fruit', 'broom', 'brimstone', 'and', 'dried', 'herb', 'the', 'palate', 'isn', 't', 'overly', 'expressive', 'offering', 'unripened', 'apple', 'citrus', 'and', 'dried', 'sage', 'alongside', 'brisk', 'acidity']
[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 0, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 0, 26, 27, 16, 17, 28, 29, 30, 31]

需要注意的是，如此得到的结果被称为encoding 编码而不是embedding 嵌入，而模型接受的输入是后者。可以使用nn.Embedding 完成前者向后者的转换。这一点在之后还会提到。

位置编码 Positional Encoding

---

注意力机制中，所有的键和查询之间是并行计算的，并不像循环神经网络那样从数据处理方式上体现了不同语速出现的次序。这会导致如下问题：

• 狗看着男孩然后……（吠叫？）
• 男孩看着狗然后……（微笑？）

为此，我们将每个token的位置也进行编码，与字符编码相加后输入后续的神经网络。

位置编码存在许多不同的的方式，Transformer中采用了被称为正弦曲线位置编码的一种绝对位置编码方式，GPT则采用了可学习位置编码，同样为绝对位置编码。除此之外还有相对位置编码和旋转位置编码。在本节中将讨论较为简单的前两种绝对编码，其他编码方式可能会在后续补充。

正弦曲线位置编码 Sinusoidal Positional Encoding

---

这是《Attention Is All You Need》中使用的编码方式，作者假设了这种编码方式可以使模型学到相对位置的信息。同时作者也尝试了可学习位置编码，并得到了几乎相同的结果。有着这种编码方式可以允许序列长度的外推，作者选择了这种方式。

在这种编码模式中，位置pos 和维度i 被考虑：

\[ \begin{aligned}P E_{(p o s, 2 i)} & =\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \\P E_{(p o s, 2 i+1)} & =\cos \left(p o s / 10000^{2 i / d_{\text {model }}}\right)\end{aligned} \]

由于使用了绝对编码，这种编码的实现完全可以不依赖于输入，十分容易实现：

• SinusoidualPositionEncoding

  class SinusoidualPositionEncoding(nn.Module):
      def __init__(self, embed_dim, max_len=512):
          super(SinusoidualPositionEncoding, self).__init__()
          self.embed_dim = embed_dim
          self.max_len = max_len
  
          position_encoding_table = torch.zeros(max_len, embed_dim)
          position = torch.arange(0, max_len).unsqueeze(1).float()
          div_term = torch.exp(torch.arange(0, embed_dim, 2).float() * -(math.log(10000.0) / embed_dim))
          position_encoding_table[:, 0::2] = torch.sin(position * div_term)
          position_encoding_table[:, 1::2] = torch.cos(position * div_term)
          position_encoding_table = position_encoding_table.unsqueeze(0)
          self.register_buffer('position_encoding_table', position_encoding_table)
      
      def forward(self, x):
          batch_size, seq_len, _ = x.size()
          return x + self.position_encoding_table[:,:seq_len, :]

使用随机生成的输入来测试代码，分别绘制输入，position_encoding_table和输出，结果如下：

正弦曲线位置编码可以提供一定的相对位置信息。为了方便计算，考虑embed_dim = 2 的情况，此时\(i = 0\)，有：

\[ \begin{aligned}P E_{(p o s, 0)} & =\sin \left(p o s \right) \\P E_{(p o s, 1)} & =\cos \left(p o s\right)\end{aligned} \]

根据和差化积公式，有：

\[ \begin{aligned}P E_{(p o s, 0)} & =\sin \left(p o s \right) = sin(pos-k)cos(k)+cos(pos-k)sin(k) \\P E_{(p o s, 1)} & =\cos \left(p o s\right) = cos(pos-k)cos(k)-sin(pos-k)sin(k)\end{aligned} \]

即对于任意\(k>0\)，\(PE_{pos}\)和\(PE_{pos-k}\)始终存在相对位置关系：

\[ \binom{P E_{pos, 0}}{P E_{pos, 1}}=\left(\begin{array}{cc}\cos k & \sin k \\-\sin k & \cos k\end{array}\right)\binom{P E_{pos-k, 0}}{P E_{pos-k, 1}} \]

可学习的位置编码 Learnable Positional Encoding

---

所谓可学习的位置编码，就是直接使用位置pos 作为位置信息输入，经过一个可学习的编码层，再与字符编码相加。下图展示了两种绝对编码的对比，前者的位置编码矩阵不会更新，因此可以提前计算，而后者对于输入的嵌入，需要生成其位置编码，然后经过处理转化为位置嵌入然后与字符嵌入相加。

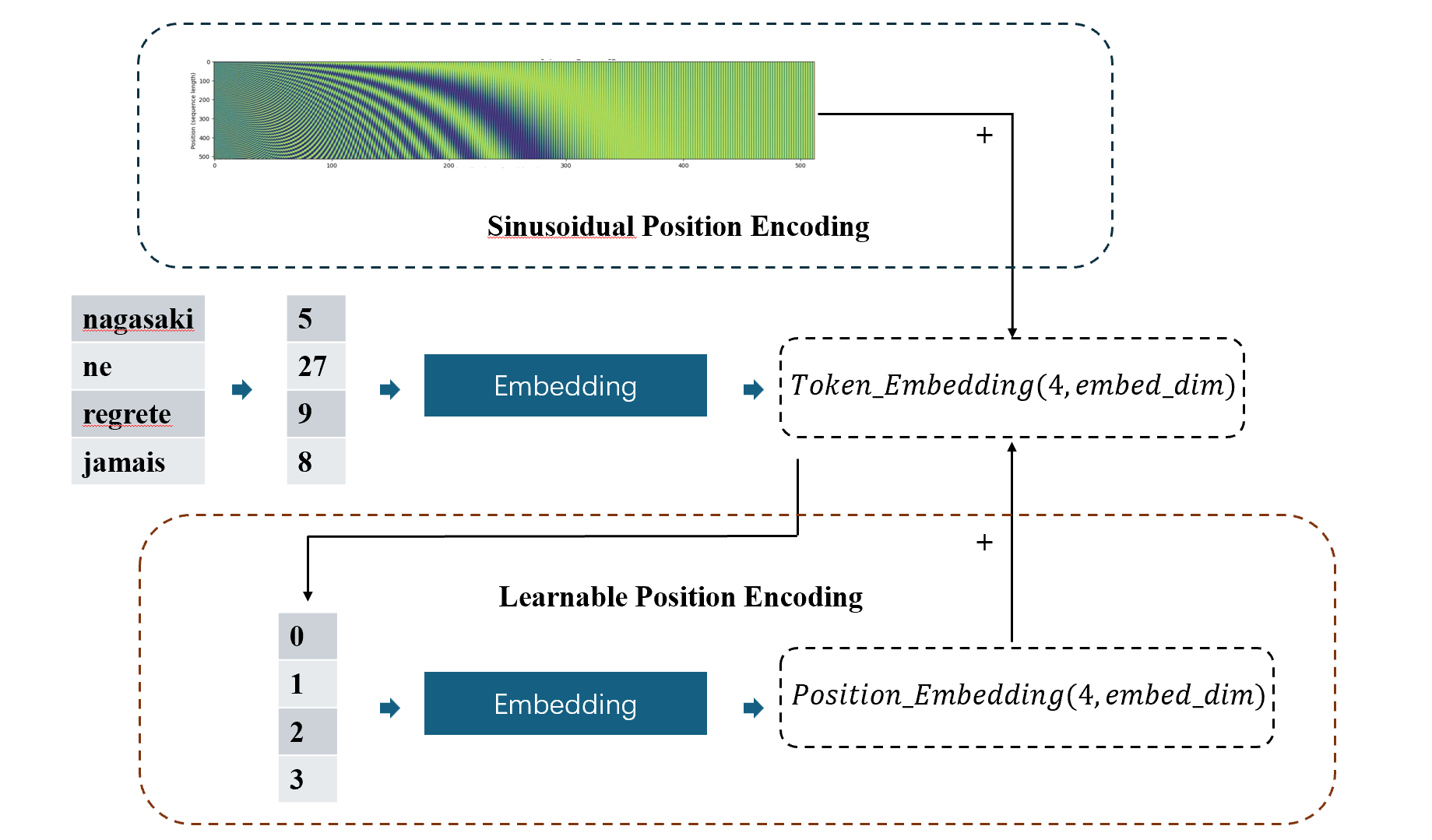
这种编码方式实现也非常简单。

• LearnablePositionEncoding

  class LearnablePositionEncoding(nn.Module):
      def __init__(self, embed_dim, max_len=512, device='cpu'):
          super(LearnablePositionEncoding, self).__init__()
          self.embed_dim = embed_dim
          self.max_len = max_len
          self.position_encoding_table = nn.Embedding(max_len, embed_dim).to(device)
      
      def forward(self, x, return_position_embedding=False):
          batch_size, seq_len, _ = x.size()
          positions = torch.arange(seq_len).long().to(x.device)
          position_embeddings = self.position_encoding_table(positions)
          if return_position_embedding:
              return x + position_embeddings, position_embeddings
          return x + position_embeddings

注意力机制

---

注意力机制 Attention

---

首先可以进行一个小的游戏

• 小游戏的代码，可以尝试在本地运行。

  import pygame
  import sys
  
  # 初始化Pygame
  pygame.init()
  
  # 设置屏幕大小
  screen_width, screen_height = 900, 600
  screen = pygame.display.set_mode((screen_width, screen_height))
  pygame.display.set_caption('猜单词游戏')
  
  # 设置字体和颜色
  font = pygame.font.Font(None, 36)
  large_font = pygame.font.Font(None, 50)
  white = (255, 255, 255)
  black = (0, 0, 0)
  gray = (200, 200, 200)
  blue = (0, 0, 255)
  red = (255, 0, 0)
  green = (0, 255, 0)
  
  # 定义句子和单词
  sentence = "The pink elephant tried to get into the car but it was too"
  words = sentence.split()
  num_words = len(words)
  
  # 定义掩蔽和点击次数
  masks = [True] * num_words
  click_counts = [0] * num_words
  
  # 掩蔽框的大小和位置
  mask_width = 120
  mask_height = 50
  padding_x = 20
  padding_y = 20
  
  # 计算单词位置，自动换行
  def calculate_word_positions():
      positions = []
      x_start, y_start = 50, 50
      x, y = x_start, y_start
      max_width = screen_width - 2 * x_start
      for word in words:
          if x + mask_width > max_width:
              x = x_start
              y += mask_height + padding_y
          positions.append((x, y))
          x += mask_width + padding_x
      return positions
  
  word_positions = calculate_word_positions()
  
  # 输入框
  input_box = pygame.Rect(50, screen_height - 100, 700, 50)
  input_active = False
  input_text = ""
  guess_word = "big"
  game_won = False
  show_result = False
  
  # 记录游戏轮数
  total_clicks = 0
  
  # 显示文本函数
  def display_text(text, font, color, position):
      text_surface = font.render(text, True, color)
      screen.blit(text_surface, position)
  
  # 显示遮蔽或单词
  def display_words():
      for i, word in enumerate(words):
          x, y = word_positions[i]
          if masks[i]:
              pygame.draw.rect(screen, gray, (x, y, mask_width, mask_height))
          else:
              display_text(word, font, black, (x + 10, y + 10))
          # 绘制单词边框
          pygame.draw.rect(screen, black, (x, y, mask_width, mask_height), 2)
  
  # 游戏主循环
  clock = pygame.time.Clock()
  running = True
  
  while running:
      screen.fill(white)
      
      # 显示单词
      display_words()
  
      # 显示输入框
      if input_active:
          pygame.draw.rect(screen, blue, input_box, 3)
      else:
          pygame.draw.rect(screen, black, input_box, 3)
      # 显示输入的文本
      display_text(input_text, font, black, (input_box.x + 10, input_box.y + 10))
  
      # 显示提示信息
      if not game_won and not show_result:
          display_text("click these block to show the word behand it,guess the last word", font, black, (50, screen_height - 150))
      if game_won:
          display_text("You win! R to play again or Q to quit this game", large_font, green if guess_word else red, (200, screen_height - 200))
      if show_result:
          display_text(f"total click times: {total_clicks}", font, black, (50, screen_height - 200))
          for i, count in enumerate(click_counts):
              display_text(f"word '{words[i]}' is clicked: {count}", font, black, (50, screen_height - 170 + i * 30))
      
      # 处理事件
      for event in pygame.event.get():
          if event.type == pygame.QUIT:
              running = False
          
          elif event.type == pygame.MOUSEBUTTONDOWN:
              mouse_x, mouse_y = event.pos
              # 检查是否点击在输入框内
              if input_box.collidepoint(mouse_x, mouse_y):
                  input_active = True
              else:
                  input_active = False
                  if not game_won and not show_result:
                      # 检查是否点击在某个遮蔽单词上
                      for i in range(num_words):
                          x, y = word_positions[i]
                          if x <= mouse_x <= x + mask_width and y <= mouse_y <= y + mask_height:
                              if masks[i]:
                                  masks[i] = False
                                  click_counts[i] += 1
                                  total_clicks += 1
                                  break
          
          elif event.type == pygame.KEYDOWN:
              if input_active and not game_won and not show_result:
                  if event.key == pygame.K_RETURN:
                      if input_text.strip().lower() == guess_word.lower():
                          game_won = True
                      else:
                          display_text("wrong guess again", font, red, (50, screen_height - 60))
                          input_text = ""
                  elif event.key == pygame.K_BACKSPACE:
                      input_text = input_text[:-1]
                  else:
                      # 只允许输入字母
                      if event.unicode.isalpha():
                          input_text += event.unicode
  
              if game_won:
                  if event.key == pygame.K_r:
                      # 重新开始游戏
                      masks = [True] * num_words
                      click_counts = [0] * num_words
                      total_clicks = 0
                      input_text = ""
                      game_won = False
                      show_result = False
                  elif event.key == pygame.K_q:
                      show_result = True
  
      pygame.display.flip()
      clock.tick(30)
  
  pygame.quit()
  sys.exit()

这个游戏界面如下，可以通过点击小块来显示小块背后的单词，以帮助你猜测句子最后的单词。

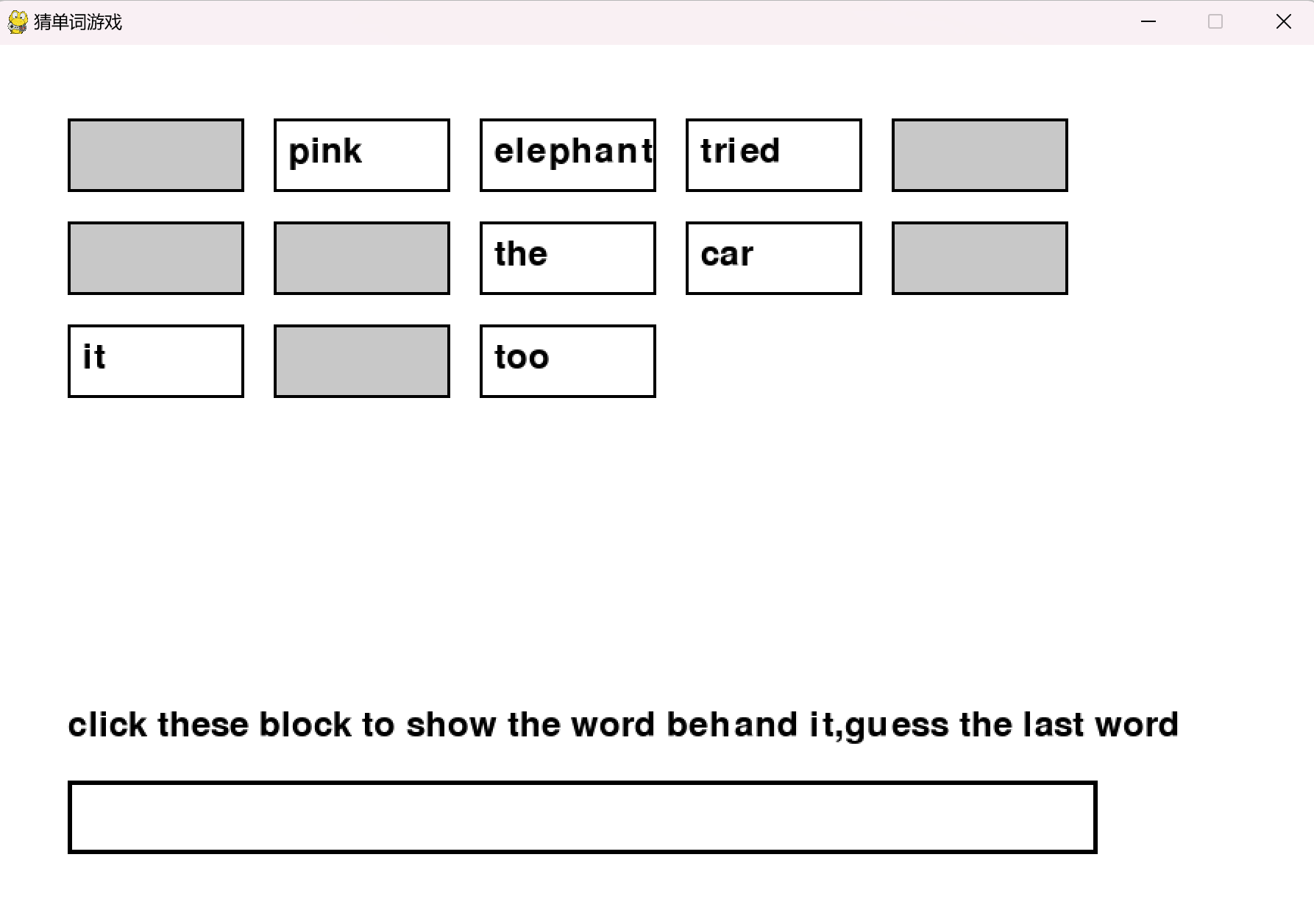
多次尝试或者与朋友一起尝试之后，你或许会发现：每个单词对于猜测出最后一个单词的作用并非等价的。如elephant和car明显比pink和the更有用。事实上，这就是注意力机制。Transformer 中的注意力机制（也称为注意力头）就是为了做到这一点而设计的。

它能够决定要从输入中的哪个位置提取信息，以便有效地提取有用的信息，而不会被不相关的细节所蒙蔽。这使得它对一系列环境具有高度适应性，因为它可以决定在推理时在哪里查找信息。

查询、键和值 Queries, Keys, and Values

---

为了完成这项任务，我们为每个单词赋予一个类似于“信心”的属性。使得elephant这个单词对自己更加自信，为下一个单词提供更多的信息；而was则对自己信心较少，为下一个单词提供更少的信息。

换句话说，我们可以将注意力头理解为一种信息查询机制。下一个单词是什么这个问题被引入到一个键值对存储系统。由查询Q与每一个键K的共振*resonance*决定权重，最终的预测结果为值V得加权求和。如下图所示。

---

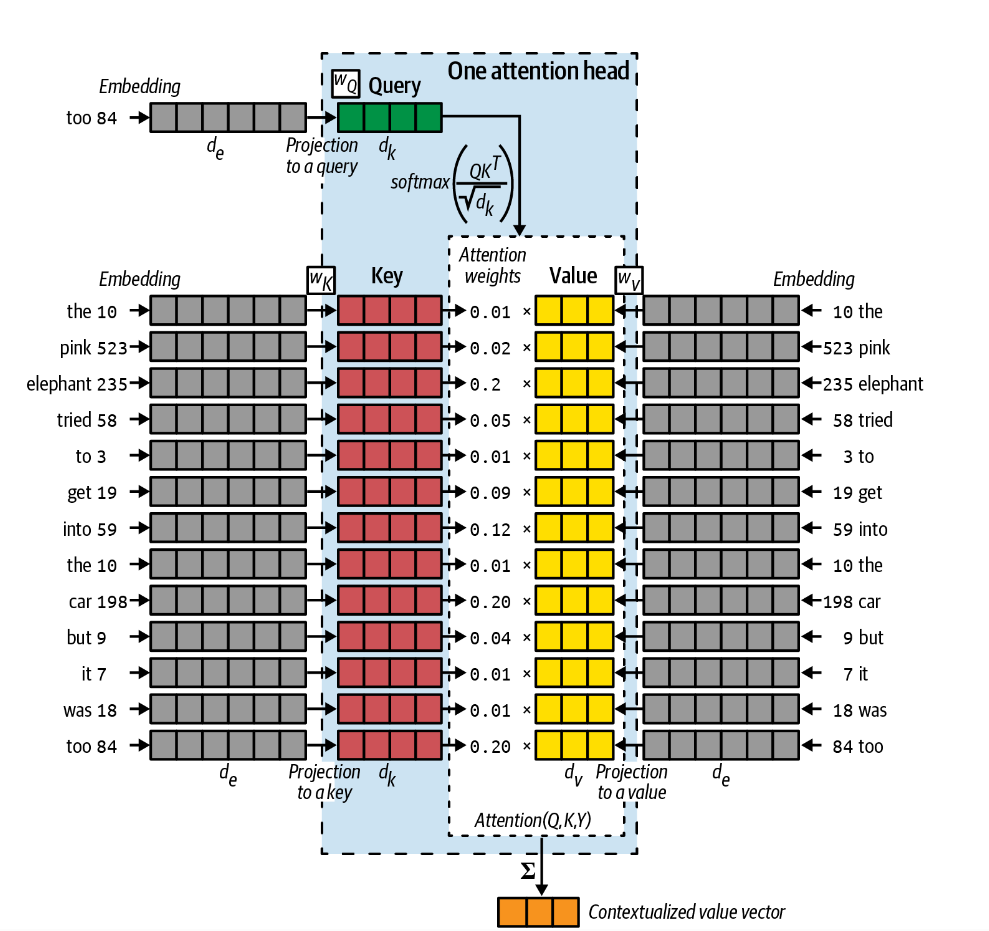
查询向量Q是当前任务得一种表示。如在训练过程中，我们得任务就是简单的预测下一个单词。在上面得例子中，它是一个单词too，与其他单词得输入方式一致，在编码后传递给权重矩阵\(W_Q\)转换为一个\(d_k\)长度的向量\(Q\)。

键向量K是句子中每个单词的表示，在编码后经过权重矩阵\(W_K\)，所有的K都转换为一个\(d_k\times \text{键的数量}\)的矩阵\(K\)。

在注意力头中，使用点积计算权重；按照\(d_k\)缩放以保证方差稳定；最终经过softmax以保证总和为1：

\[ w_i = softmax(\frac{v_k\cdot v_q}{\sqrt{d_k}})；W_V= softmax(\frac{Q\cdot K^T}{\sqrt{d_k}}) \]

值向量V也是句子中单词的表示，可以将它们视为每个单词的未加权贡献。也经过权重矩阵\(W_V\)转化为一个\(d_v\times{值的数量}\)的向量\(V\)。但是值向量不一定必须与键和查询具有相同的长度，只是为了简单起见，通常这样做。

由此，注意力attention被定义为：

\[ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V \]

为了从注意力头获得最终的输出向量，注意力被求和以给出长度为 \(d_v\) 的向量。该上下文向量捕获了句子中单词的混合意见，以预测接下来的单词。

---

我们给出一个这种计算的简略例子，以帮助在数学上的理解，如假设\(Q，K，V\)三个矩阵分别如下：

\[ Q=\left[\begin{array}{llll} 1 & 0 & 2 & 1 \end{array}\right]，K=\left[\begin{array}{llll} 1 & 0 & 2 & 1 \\ 0 & 1 & 1 & 0 \\ 2 & 1 & 0 & 2 \\ 1 & 0 & 2 & 1 \end{array}\right]，V=\left[\begin{array}{lll} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 0 & 1 & 2 \\ 1 & 0 & 1 \end{array}\right] \]

首先计算\(Q K^T\)：

\[ Q K^T=\left[\begin{array}{llll} 1 & 0 & 2 & 1 \end{array}\right] \times\left[\begin{array}{llll} 1 & 0 & 2 & 1 \\ 0 & 1 & 1 & 0 \\ 2 & 1 & 0 & 2 \\ 1 & 0 & 2 & 1 \end{array}\right]=\left[\begin{array}{llll} 6 & 2 & 4 & 6 \end{array}\right] \]

然后进行缩放：

\[ \frac{Q K^T}{\sqrt{d_k}}=\frac{\left[\begin{array}{llll} 6 & 2 & 4 & 6 \end{array}\right]}{2}=\left[\begin{array}{llll} 3 & 1 & 2 & 3 \end{array}\right] \]

并基于softmax 计算注意力权重：

\[ \operatorname{softmax}\left(\left[\begin{array}{llll} 3 & 1 & 2 & 3 \end{array}\right]\right)=\left[\begin{array}{llll} 0.36 & 0.05 & 0.13 & 0.36 \end{array}\right] \]

最后计算值的加权和：

\[ \left[\begin{array}{llll} 0.36 & 0.05 & 0.13 & 0.36 \end{array}\right] \times\left[\begin{array}{lll} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 0 & 1 & 2 \\ 1 & 0 & 1 \end{array}\right] = \begin{array}{ccc} {[1.18} & 0.18 & 1.34] \end{array} \]

因此最终的输出为：

\[ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) V = \begin{array}{ccc} {[1.18} & 0.18 & 1.34] \end{array} \]

多注意力头

---

Transformer架构的一个优势是能够同时在多个设备上并行计算，这很大程度上得益于多注意力头的机制。多注意力头结构如下，即每个注意力头给出自己的输出，然后将结果拼接并进行进一步的处理。

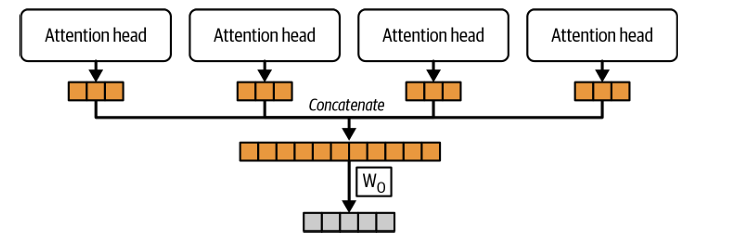
代码实现：多注意力头

---

注意力头

---

实现一个如上所述的注意力头十分简单，很容易发现，整个注意力头中可更新矩阵只包括三个矩阵，即三个线性层。因此我们可以实现以下代码：

我们定义三个函数：

• __init__：用来初始化类，我们接受embed_diam, v_dim=None, k_dim=None, out_proj=False, device="cpu" 这些参数。类中包含三个或者四个线性层，取决于是否进行输出投影。

• forward：用于进行每次注意力计算，计算公式就是已经提到的注意力公式。掩蔽用于阻止某些单词的权重，在未来我们会解释。

• to ：实际上是一个很不负责任的函数，目的是替换注意力头所在的设备。

• AttentionHead

  import torch
  import torch.nn as nn
  import torch.nn.functional as F
  
  class AttentionHead(nn.Module):
      def __init__(self, embed_diam, v_dim=None, k_dim=None, out_proj=False, device="cpu"):
          super(AttentionHead, self).__init__()
          if v_dim is None:
              v_dim = embed_diam
          if k_dim is None:
              k_dim = embed_diam
          q_dim = k_dim
          self.w_K = nn.Linear(embed_diam, k_dim).to(device)
          self.w_v = nn.Linear(embed_diam, v_dim).to(device)
          self.w_q = nn.Linear(embed_diam, q_dim).to(device)
          self.softmax = F.softmax
          self.embed_diam = embed_diam
          self.v_dim = v_dim
          self.q_dim = q_dim
          self.k_dim = k_dim
          self.if_out_proj = out_proj
  
          if out_proj:
              self.out_proj = nn.Linear(
                  v_dim, embed_diam
              ).to(device)  # 为了保证输出的维度和输入的维度一致，所以有时需要一个线性变换
  
      def forward(self, key, value, query, mask=None):
          key = self.w_K(key)
          value = self.w_v(value)
          query = self.w_q(query)
          scores = torch.matmul(query, key.transpose(-2, -1)) / torch.sqrt(
              torch.tensor(self.k_dim, dtype=torch.float32)
          )
          if mask is not None:
              # 如果应用掩蔽
              scores = scores.masked_fill(mask == 0, -torch.inf)
          attention = self.softmax(scores, dim=-1)
          attention = torch.matmul(attention, value)
          if self.if_out_proj:
              attention = self.out_proj(attention)
          return attention
      
      def to(self,device):
          self.w_K.to(device)
          self.w_v.to(device)
          self.w_q.to(device)
          if self.if_out_proj:
              self.out_proj.to(device)
          return self

代码十分简单，有两点需要注意的。其一是out_proj ，这一般被称为输出投影，旨在将输出与输入的维度统一。其二是mask ，一般被称为因果掩蔽，之后我们会讨论。

多注意力头

---

在定义完成注意力头之后，多注意力头也很容易定义，只需要将键，值和查询依次通过所有注意力头，然后拼接在一起即可。

• MultiAttentionHead

  import torch
  import torch.nn as nn
  from attentionHead import AttentionHead
  
  class MultiAttentionHead(nn.Module):
      def __init__(
          self, embed_dim, num_heads, k_dim=None, v_dim=None, out_proj=False, device="cpu"
      ):
          super(MultiAttentionHead, self).__init__()
          self.embed_dim = embed_dim
          self.num_heads = num_heads
          self.device = device
          self.attention_heads = nn.ModuleList(
              [
                  AttentionHead(embed_dim, k_dim=k_dim, v_dim=v_dim, device=device)
                  for _ in range(num_heads)
              ]
          )
          self.out_proj = nn.Linear(num_heads * v_dim, embed_dim).to(device) if out_proj else None
  
      def forward(self, key, value, query, mask=None):
          attention_heads = [
              attention_head(key, value, query, mask)
              for attention_head in self.attention_heads
          ]
          result =  torch.cat(attention_heads, dim=-1)
          if self.out_proj != None:
              result = self.out_proj(result)
          return result
  
      def to(self, device):
          for attention_head in self.attention_heads:
              attention_head.to(device)
          self.device = device
          return self

可以测试类是否正常工作：

if __name__ == "__main__":
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    multi_attention_head = MultiAttentionHead(
        embed_dim=128, num_heads=8, k_dim=64, v_dim=64, device=device
    )
    key = torch.randn(16, 10, 128).to(device)
    value = torch.randn(16, 10, 128).to(device)
    query = torch.randn(16, 10, 128).to(device)
    attention = multi_attention_head(key, value, query)
    print(attention.shape)
---
torch.Size([16, 10, 512])

可以看到512维的向量正是8个64维的向量（没有进行输出投影）拼接而成。有一点需要注意的是embed_dim 是每个注意力头的embed维度。

使用torch.nn.MultiheadAttention

---

事实上，pytorch提供了多注意里头的模块，定义为：

torch.nn.MultiheadAttention(embed_dim, num_heads, dropout=0.0, bias=True, add_bias_kv=False, add_zero_attn=False, kdim=None, vdim=None, batch_first=False, device=None, dtype=None)

• Pytorch提供的文档的翻译

  • embed_dim – 模型的总维度。
  • num_heads – 并行注意力头的数量。注意，embed_dim 将会在这些头之间拆分（即每个头的维度为 embed_dim // num_heads）。
  • dropout – 对注意力输出权重应用的 dropout 概率。默认不使用。
  • bias – 如果指定，将会为输入/输出投影层添加偏置。默认值为 True。
  • add_bias_kv – 如果指定，将会为键和值序列在 dim=0 上添加偏置。默认值为 False。
  • add_zero_attn – 如果指定，将会在键和值序列的 dim=1 上添加一组全零的批次。默认值为 False。
  • kdim – 键的特征总数。默认使用 kdim=embed_dim。
  • vdim – 值的特征总数。默认使用 vdim=embed_dim。
  • batch_first – 如果为 True，则输入和输出张量的形状为 (batch, seq, feature)。默认值为 False，形状为 (seq, batch, feature。

  ---

  forward(query, key, value, key_padding_mask=None, need_weights=True, attn_mask=None, average_attn_weights=True, is_causal=False)

  • query (Tensor) – 查询嵌入，形状为 (L, E_q)（对于未批次输入），或者 (L, N, E_q) 当 batch_first=False 或者 (N, L, E_q) 当 batch_first=True。其中，L 为目标序列长度，N 为批次大小，E_q 为查询嵌入的维度 embed_dim。
  • key (Tensor) – 键嵌入，形状为 (S, E_k)（未批次输入），或者 (S, N, E_k) 当 batch_first=False，或者 (N, S, E_k) 当 batch_first=True。其中，S 为源序列长度，N 为批次大小，E_k 为键嵌入维度 kdim。
  • value (Tensor) – 值嵌入，形状为 (S, E_v)（未批次输入），或者 (S, N, E_v) 当 batch_first=False，或者 (N, S, E_v) 当 batch_first=True。其中，S 为源序列长度，N 为批次大小，E_v 为值嵌入维度 vdim。
  • key_padding_mask (Optional[Tensor]) – 如果指定，则为一个掩码，形状为 (N, S)，表示哪些键在注意力计算时将被忽略。对于未批次的查询，形状应为 (S)。支持二进制掩码和浮点掩码。对于二进制掩码，True 表示对应的键值将被忽略。对于浮点掩码，将会直接加到对应的键值上。
  • need_weights (bool) – 如果指定，将在返回 attn_outputs 的同时返回 attn_output_weights。设置 need_weights=False 可以使用优化后的 scaled_dot_product_attention 并达到最佳性能。默认值为 True。
  • attn_mask (Optional[Tensor]) – 如果指定，将应用于防止某些位置的注意力。形状必须为 (L, S) 或者 (N⋅num_heads, L, S)，其中 N 为批次大小，L 为目标序列长度，S 为源序列长度。2D 掩码将会广播到整个批次，而 3D 掩码允许为批次中的每个条目使用不同的掩码。支持二进制和浮点掩码。二进制掩码中，True 值表示不允许对对应位置进行注意力。对于浮点掩码，掩码值将会加到注意力权重上。如果同时提供 attn_mask 和 key_padding_mask，它们的类型应该匹配。
  • average_attn_weights (bool) – 如果为 True，返回的 attn_weights 将在各个头之间进行平均。否则，attn_weights 将会单独返回每个头的权重。此标志仅在 need_weights=True 时有效。默认值为 True（即在头之间平均权重）。
  • is_causal (bool) – 如果指定，将会应用一个因果掩码作为注意力掩码。默认值为 False。警告：is_causal 提供了一个提示，表明 attn_mask 是因果掩码。提供错误的提示可能导致执行错误，包括正向和反向兼容性问题。

  ---

  • attn_output – 注意力输出，形状为 (L, E)（未批次输入），或者 (L, N, E) 当 batch_first=False，或者 (N, L, E) 当 batch_first=True。其中，L 为目标序列长度，N 为批次大小，E 为嵌入维度 embed_dim。
  • attn_output_weights – 仅在 need_weights=True 时返回。如果 average_attn_weights=True，返回的注意力权重在各个头之间进行平均，形状为 (L, S)（未批次输入）或者 (N, L, S)。如果 average_attn_weights=False，则返回每个头的注意力权重，形状为 (num_heads, L, S)（未批次输入）或者 (N, num_heads, L, S)。

尝试实现一个示例：

torch_multi_attention_head = nn.MultiheadAttention(
        embed_dim=128, num_heads=8, batch_first=True
    ).to(device)
torch_attension = torch_multi_attention_head(query, key, value)
print(torch_attension[0].shape)
---
torch.Size([16, 10, 128])

在使用这个函数的时候必须注意，其参数中的embed_dim, kdim, vdim可能与文档中描述的作用并不相同。具体来说，这个类的计算可能经过一个如下过程：

if self.fused_attn:
    x = F.scaled_dot_product_attention(
        q, k, v,
        dropout_p=self.attn_drop.p if self.training else 0.,
    )
else:
    q = q * self.scale
    attn = q @ k.transpose(-2, -1)
    attn = attn.softmax(dim=-1)
    attn = self.attn_drop(attn)
    x = attn @ v

其中，q,k,v 的形状均为(B, num_heads, N, head_dim) ，其中num_heads*head_dim = embed_dim 。也就是原输入的embedding被拆分到不同的注意力头。

这里有一个比较有争议的地方，那就是线性层的设置问题。原文描述：

we found it beneficial to linearly project the queries, keys and values h times with different, learned linear projections to dk…

也就是说，每个注意力头的线性层可能是不同的，正如在之前的代码中所实现的那样。而如今，很多实现使用的方式则类似于先使用三个线性层完成映射，再将得到的键，值，查询拆分到不同的注意力头，不同的注意力头仅仅计算注意力，不再进行权重计算。

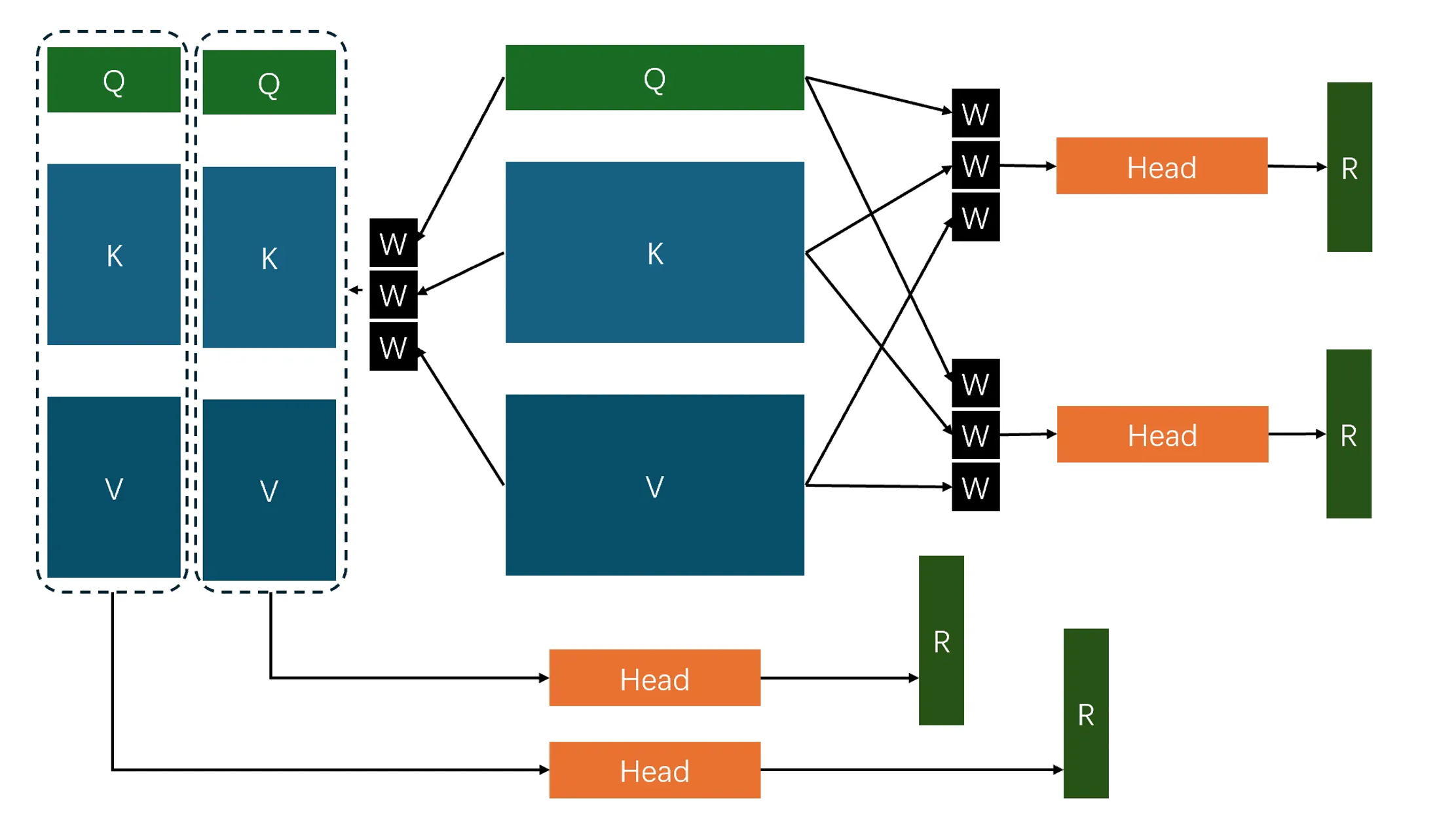
图中向右的路径为第一种实现，向左的路径为第二种实现。

\[ \begin{aligned}& \operatorname{MultiHead}(Q, K, V)=\operatorname{Concat}\left(\text { head }_1, \ldots, \text { head }_{\mathrm{h}}\right) W^O \\& \text { where head }_{\mathrm{i}}=\operatorname{Attention}\left(Q W_i^Q, K W_i^K, V W_i^V\right)\end{aligned} \]

中明确显示了完整的键矩阵，值矩阵和查询向量被输入到每一个头中。

参考torch的实现，优化多注意力头

---

相比于最初直接根据原理实现的多注意力头，有几点优化方向是值得考虑的：

• 增加偏置的选项，这是因为线性层的计算方式为：\(f(x) = Wx+B\)，其中\(B\)即为偏置。在attention的公式中，显然没有使用偏置。为此增加此选项。
• 增加dropout和归一化层的选项，关于其作用比较繁杂，可以自己查询。
• 增加use_fused_attn 选项，允许使用PyTorch 的 scaled_dot_product_attention函数来加速注意力计算。
• 增加is_causal 选项，以实施因果掩蔽，之后会讨论这一部分。
• 将原本的基于多个注意力类计算的过程直接集成在当前类中，理论上不会增加神经网络的计算速度，但将有效提升注意力的计算速度。同时，这种计算方式将允许使用scaled_dot_product_attention 函数。
• 允许使用布尔类型和浮点类型的掩蔽。

优化后的代码如下，这是前文所描述的第一种实现方式的代码。代码中分离了神经网络计算和注意力计算，即分离了\(Q_{im} = Q W_i^Q, K_{im}=K W_i^K, V_{im}=V W_i^V\)和\(\operatorname{head}_{\mathrm{i}}=\operatorname{Attention}\left(Q_{im}, K_{im}, V_{im}\right)\)两个过程。是否使用scaled_dot_product_attention 是可选的，但实际上，这个函数的实现基本上与else 部分描述的计算方式相同。

• MultiAttentionHead_A

  class MultiAttentionHead_A(nn.Module):
      '''
      A版本的多注意力头，这一版本的注意力头将键，值和查询完整的输入每一个注意力头中，每一个注意力头中都有完整的线性层，然后将每一个注意力头的输出拼接在一起，最后通过一个线性层进行输出。
  
      ### 参数：
      - embed_dim (int)：输入嵌入的维度大小。
      - num_heads (int)：注意力头的数量。
      - k_dim (int, 可选)：键（Key）和查询（Query）的维度大小。如果为 None，则使用 embed_dim 作为默认值。
      - v_dim (int, 可选)：值（Value）的维度大小。如果为 None，则使用 embed_dim 作为默认值。
      - out_proj (bool, 默认值为 False)：是否对输出进行线性投影，将输出向量的长度从v_dim映射到embed_dim。如果为 True，则在输出时应用一个线性层。
      - device (str, 默认值为 "cpu")：指定模型运行的设备，如 "cpu" 或 "cuda"。
      - qkv_bias (bool, 默认值为 False)：是否在键、值和查询的线性层中使用偏置（Bias）。
      - attn_drop (float, 默认值为 0.0)：注意力权重的 Dropout 概率。
      - proj_drop (float, 默认值为 0.0)：输出投影的 Dropout 概率。
      - norm_layer (nn.Module, 默认值为 nn.LayerNorm)：用于键和值的归一化层类型，只有在qk_norm为真时norm_layer才会启用。
      - qk_norm (bool, 默认值为 False)：是否对键和查询进行归一化处理，只有在qk_norm为真时norm_layer才会启用。
      - use_fused_attn (bool, 默认值为 False)：是否使用 PyTorch 的 scaled_dot_product_attention 函数来加速注意力计算。
      - is_causal (bool, 默认值为 False)：是否启用因果遮掩，用于防止注意力机制关注未来的时间步，在使用因果掩蔽时必须保证不输入mask，否则会根据mask进行掩蔽。
  
      ### 方法：
      - __init__(self, embed_dim, num_heads, ...)
          初始化 MultiAttentionHead_A 类，实例化内部的多头注意力机制、前馈神经网络、Dropout 和归一化层。
      - forward(self, key, value, query, mask=None, return_attention=False)
          - 输入：
              - key (Tensor)：键（Key）的张量，形状为 (batch_size, sequence_length, k_dim)。
              - value (Tensor)：值（Value）的张量，形状为 (batch_size, sequence_length, v_dim)。
              - query (Tensor)：查询（Query）的张量，形状为 (batch_size, sequence_length, k_dim)。
              - mask (Tensor, 可选)：注意力权重的遮掩张量，形状为 (sequence_length, sequence_length) 或 (batch_size, sequence_length, sequence_length)。
              - return_attention (bool, 可选)：是否返回注意力权重，默认值为 False。
          - 输出：
              - 如果 return_attention=True，返回两项：
                  - result：多注意力头的输出，形状为 (batch_size, sequence_length, v_dim)。
                  - attention：注意力权重的均值，形状为 (batch_size, num_heads, sequence_length, sequence_length)。
              - 如果 return_attention=False，仅返回 result。
      '''
  
      def __init__(
          self,
          embed_dim,
          num_heads,
          k_dim=None,
          v_dim=None,
          out_proj=False,
          device="cpu",
          qkv_bias: bool = False,
          attn_drop: float = 0.0,
          proj_drop: float = 0.0,
          norm_layer: nn.Module = nn.LayerNorm,
          qk_norm: bool = False,
          use_fused_attn: bool = False,
          is_causal: bool = False,
      ):
          super(MultiAttentionHead_A, self).__init__()
          self.embed_dim = embed_dim
          self.k_dim = k_dim if k_dim is not None else embed_dim
          self.v_dim = v_dim if k_dim is not None else embed_dim
          self.if_out_proj = out_proj
  
          self.num_heads = num_heads
  
          self.device = device
  
          self.use_fused_attn = use_fused_attn
  
          self.is_causal = is_causal
  
          self.qk_norm = qk_norm
  
          self.attn_drop = nn.Dropout(attn_drop)
          self.proj_drop = nn.Dropout(proj_drop)
          self.attention_heads = nn.ModuleList(
              [
                  nn.ModuleList(
                      [
                          nn.Linear(embed_dim, k_dim, bias=qkv_bias),
                          nn.Linear(embed_dim, v_dim, bias=qkv_bias),
                          nn.Linear(embed_dim, k_dim, bias=qkv_bias),
                      ]
                  )
                  for _ in range(num_heads)
              ]
          )
          self.out_proj = (
              nn.Linear(num_heads * v_dim, embed_dim) if out_proj else nn.Identity()
          )
  
          self.v_norm_layer = norm_layer(self.v_dim) if qk_norm else nn.Identity()
          self.k_norm_layer = norm_layer(self.k_dim) if qk_norm else nn.Identity()
  
          self.to(device)
  
      def forward(self, key, value, query, mask=None, return_attention=False):
          keys, values, queries = self.before_ultiattention(key, value, query)
          batch_size, seq_len, k_dim = value.shape
  
          if self.qk_norm:
              keys = self.k_norm_layer(keys)
              values = self.v_norm_layer(values)
  
          if self.use_fused_attn:
              x = F.scaled_dot_product_attention(
                  queries,
                  keys,
                  values,
                  dropout_p=self.attn_drop.p if self.training else 0.0,
                  attn_mask=mask,
                  is_causal=self.is_causal,
              )
          else:
              L, S = queries.size(-2), keys.size(-2)
              attn_bias = torch.zeros(L, S, dtype=queries.dtype).to(self.device)
              if self.is_causal and mask is None:
                  assert mask is None
                  temp_mask = torch.ones(L, S, dtype=torch.bool).tril(diagonal=0)
                  attn_bias.masked_fill_(temp_mask.logical_not(), float("-inf"))
                  attn_bias.to(queries.dtype)
              if mask is not None:
                  if mask.dtype == torch.bool:
                      attn_bias.masked_fill_(mask.logical_not(), float("-inf"))
                  else:
                      attn_bias += mask
              scale_factor = 1 / torch.sqrt(torch.tensor(queries.size(-1)))
              attn = queries @ keys.transpose(-2, -1) * scale_factor
              attn += attn_bias
              attn = torch.softmax(attn, dim=-1)
              attn = self.attn_drop(attn)
              x = attn @ values
  
          x = x.transpose(1, 2).reshape(batch_size, -1, self.num_heads * self.v_dim)
          x = self.out_proj(x)
          x = self.proj_drop(x)
          if return_attention and not self.use_fused_attn:
              return x, attn
          return x, None
  
      def before_ultiattention(self, key, value, query):
          keys = torch.zeros(key.shape[0], self.num_heads, key.shape[1], self.k_dim).to(
              self.device
          )
          values = torch.zeros(
              value.shape[0], self.num_heads, value.shape[1], self.k_dim
          ).to(self.device)
          queries = torch.zeros(
              query.shape[0], self.num_heads, query.shape[1], self.k_dim
          ).to(self.device)
          for i in range(self.num_heads):
              m_key = self.attention_heads[i][0](key)
              m_value = self.attention_heads[i][1](value)
              m_query = self.attention_heads[i][2](query)
              keys[:, i] = m_key
              values[:, i] = m_value
              queries[:, i] = m_query
          return keys, values, queries

关于输出映射，实际上在每一个注意力头中使用输出映射和在最终拼接之后使用注意力映射本质上是等价的。

如果不使用输出映射，最终输出的尺寸是\((batch\_size, number \ of \ query's \ tokens,v\_dim\times num\_heads)\)。

key = torch.randn(16, 10, 128).to(device)
value = torch.randn(16, 10, 128).to(device)
query = torch.randn(16, 2, 128).to(device)
multi_attention_head_A = MultiAttentionHead_A(
    embed_dim=128,    num_heads=8,    k_dim=64,    
    v_dim=64,    out_proj=False,    device=device,    
    qkv_bias=True,    attn_drop=0.1,    proj_drop=0.1,    
    norm_layer=nn.LayerNorm,    qk_norm=True,    use_fused_attn=True,
)
result = multi_attention_head_A(key, value, query)
print(result.shape)
---
torch.Size([16, 2, 512])

经过测试，这种实现方式的参数量略多于pytorch中的实现，性能没有太大差异。

---

为了方便之后测试，同样也实现一版第二种实现方式的多注意力头。只需要在第一种多注意力头上做一些调整：

• MultiAttentionHead_B

  class MultiAttentionHead_B(nn.Module):
      '''
      B版本的多注意力头，这一版本的注意力头将键，值和查询完整的输入线性层中，然后将结果平分到每一个注意力头中，每一个注意力头中没有线性层，然后将每一个注意力头的输出拼接在一起，最后通过一个线性层进行输出。
  
      ### 参数：
      - embed_dim (int)：输入嵌入的维度大小，注意如果不使用k_dim和v_dim这个大小必须是注意力头的倍数。
      - num_heads (int)：注意力头的数量。
      - k_dim (int, 可选)：键（Key）和查询（Query）的维度大小，这个大小必须是注意力头的倍数。如果为 None，则使用 embed_dim 作为默认值。
      - v_dim (int, 可选)：值（Value）的维度大小，这个大小必须是注意力头的倍数。如果为 None，则使用 embed_dim 作为默认值。
      - out_proj (bool, 默认值为 False)：是否对输出进行线性投影，将输出向量的长度从v_dim映射到embed_dim。如果为 True，则在输出时应用一个线性层。
      - device (str, 默认值为 "cpu")：指定模型运行的设备，如 "cpu" 或 "cuda"。
      - qkv_bias (bool, 默认值为 False)：是否在键、值和查询的线性层中使用偏置（Bias）。
      - attn_drop (float, 默认值为 0.0)：注意力权重的 Dropout 概率。
      - proj_drop (float, 默认值为 0.0)：输出投影的 Dropout 概率。
      - norm_layer (nn.Module, 默认值为 nn.LayerNorm)：用于键和值的归一化层类型，只有在qk_norm为真时norm_layer才会启用。
      - qk_norm (bool, 默认值为 False)：是否对键和查询进行归一化处理，只有在qk_norm为真时norm_layer才会启用。
      - use_fused_attn (bool, 默认值为 False)：是否使用 PyTorch 的 scaled_dot_product_attention 函数来加速注意力计算。
      - is_causal (bool, 默认值为 False)：是否启用因果遮掩，用于防止注意力机制关注未来的时间步，在使用因果掩蔽时必须保证不输入mask，否则会根据mask进行掩蔽。
  
      ### 方法：
      - __init__(self, embed_dim, num_heads, ...)
          初始化 MultiAttentionHead_B 类，实例化内部的多头注意力机制、前馈神经网络、Dropout 和归一化层。
      - forward(self, key, value, query, mask=None, return_attention=False)
          - 输入：
              - key (Tensor)：键（Key）的张量，形状为 (batch_size, sequence_length, k_dim)。
              - value (Tensor)：值（Value）的张量，形状为 (batch_size, sequence_length, v_dim)。
              - query (Tensor)：查询（Query）的张量，形状为 (batch_size, sequence_length, k_dim)。
              - mask (Tensor, 可选)：注意力权重的遮掩张量，形状为 (sequence_length, sequence_length) 或 (batch_size, sequence_length, sequence_length)。
              - return_attention (bool, 可选)：是否返回注意力权重，默认值为 False。
          - 输出：
              - 如果 return_attention=True，返回两项：
                  - result：多注意力头的输出，形状为 (batch_size, sequence_length, v_dim)。
                  - attention：注意力权重的均值，形状为 (batch_size, num_heads, sequence_length, sequence_length)。
              - 如果 return_attention=False，仅返回 result。
      '''
  
      def __init__(
          self,
          embed_dim,
          num_heads,
          k_dim=None,
          v_dim=None,
          out_proj=False,
          device="cpu",
          qkv_bias: bool = False,
          attn_drop: float = 0.0,
          proj_drop: float = 0.0,
          norm_layer: nn.Module = nn.LayerNorm,
          qk_norm: bool = False,
          use_fused_attn: bool = False,
          is_causal: bool = False,
      ):
          super(MultiAttentionHead_B, self).__init__()
          self.embed_dim = embed_dim
          self.k_dim = k_dim if k_dim is not None else embed_dim
          self.v_dim = v_dim if k_dim is not None else embed_dim
          self.if_out_proj = out_proj
  
          self.num_heads = num_heads
  
          self.device = device
  
          self.use_fused_attn = use_fused_attn
  
          self.is_causal = is_causal
  
          self.qk_norm = qk_norm
  
          self.attn_drop = nn.Dropout(attn_drop)
          self.proj_drop = nn.Dropout(proj_drop)
          self.attention_heads = nn.ModuleList(
              [
                  nn.Linear(embed_dim, k_dim, bias=qkv_bias),
                  nn.Linear(embed_dim, v_dim, bias=qkv_bias),
                  nn.Linear(embed_dim, k_dim, bias=qkv_bias),
              ]
          )
          self.out_proj = nn.Linear(v_dim, embed_dim) if out_proj else nn.Identity()
  
          self.v_norm_layer = norm_layer(self.v_dim//self.num_heads) if qk_norm else nn.Identity()
          self.k_norm_layer = norm_layer(self.k_dim//self.num_heads) if qk_norm else nn.Identity()
  
          self.to(device)
  
      def forward(self, key, value, query, mask=None, return_attention=False):
          keys, values, queries = self.before_ultiattention(key, value, query)
          batch_size, seq_len, k_dim = value.shape
  
          if self.use_fused_attn:
              x = F.scaled_dot_product_attention(
                  queries,
                  keys,
                  values,
                  dropout_p=self.attn_drop.p if self.training else 0.0,
                  attn_mask=mask,
                  is_causal=self.is_causal,
              )
              attn = None
          else:
              L, S = queries.size(-2), keys.size(-2)
              attn_bias = torch.zeros(L, S, dtype=queries.dtype).to(self.device)
              if self.is_causal and mask is None:
                  assert mask is None
                  temp_mask = (
                      torch.ones(L, S, dtype=torch.bool).tril(diagonal=0).to(self.device)
                  )
                  attn_bias.masked_fill_(temp_mask.logical_not(), float("-inf"))
                  attn_bias.to(queries.dtype)
              if mask is not None:
                  if mask.dtype == torch.bool:
                      attn_bias.masked_fill_(mask.logical_not(), float("-inf"))
                  else:
                      attn_bias += mask
              scale_factor = 1 / torch.sqrt(
                  torch.tensor(queries.size(-1), device=self.device)
              )
              attn = queries @ keys.transpose(-2, -1) * scale_factor
              attn += attn_bias
              attn = torch.softmax(attn, dim=-1)
              attn = self.attn_drop(attn)
              x = attn @ values
  
          x = x.transpose(1, 2).reshape(batch_size, -1, self.v_dim)
          x = self.out_proj(x)
          x = self.proj_drop(x)
  
          if return_attention:
              return x, attn
          return x
  
      def before_ultiattention(self, key, value, query):
          m_key = self.attention_heads[0](key)
          m_value = self.attention_heads[1](value)
          m_query = self.attention_heads[2](query)
          keys = m_key.reshape(
              key.shape[0], self.num_heads, key.shape[1], self.k_dim // self.num_heads
          )
          values = m_value.reshape(
              value.shape[0], self.num_heads, value.shape[1], self.v_dim // self.num_heads
          )
          queries = m_query.reshape(
              query.shape[0], self.num_heads, query.shape[1], self.k_dim // self.num_heads
          )
          keys = self.k_norm_layer(keys)
          values = self.v_norm_layer(values)
          return keys, values, queries

这种注意力头要求embed_dim, k_dim, v_dim必须是num_heads的倍数（如果同时使用了后两个，则不要求embed_dim是num_heads的倍数）。如果不使用输出映射，最终输出的尺寸为：\((batch\_size, number \ of \ query's \ tokens,v\_dim)\)

key = torch.randn(16, 10, 128).to(device)
value = torch.randn(16, 10, 128).to(device)
query = torch.randn(16, 2, 128).to(device)
multi_attention_head_A = MultiAttentionHead_A(
    embed_dim=128,    num_heads=8,    k_dim=64,    
    v_dim=64,    out_proj=False,    device=device,    
    qkv_bias=True,    attn_drop=0.1,    proj_drop=0.1,    
    norm_layer=nn.LayerNorm,    qk_norm=True,    use_fused_attn=True,
)
result = multi_attention_head_A(key, value, query)
print(result.shape)
---
torch.Size([16, 2, 64])

经测试，这种实现的性能略差官方实现和第一种实现，原因不明。如果需要使用第二种实现，建议使用pytorch的官方实现。

掩蔽

---

根据注意力机制的描述，所有的值提供的信息都会被考虑。但这未必总是合理的。有些时候，我们可能希望手动的避免某些键值对为当前查询提供信息，对此，我们会对某些键值对进行掩蔽：

\[ \operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) MV \]

---

如我们曾经讨论过的例子，如果我们只希望前两组键值对提供信息，将在softmax 计算注意力权重之后，会与掩蔽矩阵相乘：

\[ \left[\begin{array}{llll} 0.36 & 0.05 & 0.13 & 0.36 \end{array}\right]\times\left[\begin{array}{llll} 1 & 1 & 0 & 0 \end{array}\right] = \left[\begin{array}{llll} 0.36 & 0.05 & 0 & 0 \end{array}\right] \]

最后计算值的加权和：

\[ \left[\begin{array}{llll} 0.36 & 0.05 & 0 & 0 \end{array}\right] \times\left[\begin{array}{lll} 1 & 0 & 2 \\ 2 & 1 & 0 \\ 0 & 1 & 2 \\ 1 & 0 & 1 \end{array}\right] = \begin{array}{ccc} {[0.46} & 0.05 & 0.72] \end{array} \]

因此最终的输出为：

\[ \operatorname{Attention}(Q, K, V,M)=\operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) MV = \begin{array}{ccc} {[0.46} & 0.05 & 0.72] \end{array} \]

给出了并不相同的结果。

因果掩蔽

---

因果掩蔽是掩蔽的一种特殊情况，也可以认为是在进行某些任务是，为了直接给查询提供合适的键值对而来的一种掩蔽方式。以续写任务为例：

很明显，对于查询the 应该提供信息的的只有the 一个单词。而对于单词pink ，the 和pink 都可以被考虑。如此，使用矩阵的方式表达每个查询应该依赖的键值对，即可得到因果掩蔽矩阵：

\[ M^T=\left(\begin{array}{llllllllll} 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right) \]

之所以称之为因果掩蔽矩阵，是因为该技术的设计基于保护因果关系，避免模型在训练过程中看到未来信息的方法，从而保持预测的因果顺序。而为什么有转置符号，会在之后进行解释。

必须要注意的是，在torch.nn.MultiheadAttention中，a True value indicates that the corresponding position is not allowed to attend，即使用1来表示被掩蔽的部分，这与我们之前的描述正好相反。

代码实现：掩蔽

---

之前的多注意力头中已经包括了掩蔽的实现，可以查看其效果。如果不使用use_fused_attn 原代码使用如下部分实现掩蔽。由此可见，如此实现的程序允许输入浮点类型或者布尔类型的掩蔽，或者直接在创建类时使用因果掩蔽选项。

• 掩蔽的实现

  attn_bias = torch.zeros(L, S, dtype=queries.dtype).to(self.device)
  if self.is_causal and mask is None:
      assert mask is None
      temp_mask = torch.ones(L, S, dtype=torch.bool).tril(diagonal=0)
      attn_bias.masked_fill_(temp_mask.logical_not(), float("-inf"))
      attn_bias.to(queries.dtype)
  if mask is not None:
      if mask.dtype == torch.bool:
          attn_bias.masked_fill_(mask.logical_not(), float("-inf"))
      else:
          attn_bias += mask
  scale_factor = 1 / torch.sqrt(torch.tensor(queries.size(-1)))
  attn = queries @ keys.transpose(-2, -1) * scale_factor
  attn += attn_bias

首先展示一个使用mask 的例子：

mask = torch.ones(10, 10).to(device)
mask = torch.triu(mask, diagonal=1).to(bool)
result = multi_attention_head_B(key, value, query, mask)

在进行掩蔽之前，权重矩阵：

• 未经掩蔽的矩阵

  \[ \left(\begin{array}{cccccccccc}-0.0381 & 0.5432 & -0.0118 & 0.2627 & 0.0788 & 0.1290 & -0.3541 & 0.2990 & 0.3344 & -0.0740 \\0.2167 & -0.0504 & -0.0263 & -0.1630 & -0.1355 & 0.2601 & 0.0644 & -0.0341 & -0.0834 & 0.0492 \\-0.0306 & 0.4404 & -0.2725 & 0.3975 & 0.1741 & 0.0236 & -0.1656 & 0.1605 & 0.3072 & -0.1043 \\-0.1396 & 0.0166 & 0.0363 & -0.0409 & -0.3242 & 0.0878 & 0.1644 & 0.4337 & 0.4110 & 0.2443 \\0.2115 & 0.4581 & -0.1963 & 0.7275 & -0.1038 & -0.1654 & -0.0064 & 0.1803 & 0.4861 & -0.1032 \\0.5943 & 0.0956 & -0.1599 & -0.0260 & 0.2320 & -0.1796 & -0.1026 & -0.0930 & 0.1034 & -0.1179 \\-0.2529 & 0.0564 & 0.1895 & -0.1583 & -0.0082 & 0.1960 & -0.0832 & 0.0468 & 0.1883 & 0.0880 \\0.1068 & 0.0028 & 0.2026 & -0.4659 & -0.0571 & 0.3256 & -0.1600 & 0.1143 & 0.2052 & 0.2048 \\0.0379 & 0.2223 & 0.0165 & 0.1183 & 0.1286 & -0.1690 & -0.1400 & 0.1407 & 0.0946 & -0.1528 \\0.2522 & -0.0824 & 0.2295 & 0.3596 & -0.1602 & -0.2169 & 0.0931 & -0.3860 & 0.3353 & 0.0802\end{array}\right) \]

在进行掩蔽之后，权重矩阵：

• 经过掩蔽的矩阵

  \(\left(\begin{array}{cccccccccc}-\infty & 0.5432 & -0.0118 & 0.2627 & 0.0788 & 0.1290 & -0.3541 & 0.2990 & 0.3344 & -0.0740 \\-\infty & -\infty & -0.0263 & -0.1630 & -0.1355 & 0.2601 & 0.0644 & -0.0341 & -0.0834 & 0.0492 \\-\infty & -\infty & -\infty & 0.3975 & 0.1741 & 0.0236 & -0.1656 & 0.1605 & 0.3072 & -0.1043 \\-\infty & -\infty & -\infty & -\infty & -0.3242 & 0.0878 & 0.1644 & 0.4337 & 0.4110 & 0.2443 \\-\infty & -\infty & -\infty & -\infty & -\infty & -0.1654 & -0.0064 & 0.1803 & 0.4861 & -0.1032 \\-\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -0.1026 & -0.0930 & 0.1034 & -0.1179 \\-\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & 0.0468 & 0.1883 & 0.0880 \\-\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & 0.2052 & 0.2048 \\-\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -0.1528 \\-\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty\end{array}\right)\)

或者使用因果掩蔽：

• 未经掩蔽的矩阵

  \[ \left[\begin{array}{cccccccccc}0.0559 & 0.4464 & -0.0436 & -0.1111 & 0.0050 & -0.3171 & 0.0839 & -0.1784 & -0.0082 & 0.1409 \\0.2037 & 0.2918 & 0.1126 & 0.3927 & 0.0867 & -0.3940 & 0.4468 & -0.0292 & -0.0809 & -0.0723 \\-0.0866 & -0.7469 & 0.0212 & 0.4034 & 0.0483 & 0.4977 & -0.1441 & 0.1939 & 0.1353 & -0.2094 \\-0.1088 & 0.1867 & -0.3031 & -0.7647 & 0.0023 & -0.3046 & -0.5611 & -0.3762 & 0.2211 & 0.3879 \\1.1036 & 0.6895 & 0.4887 & -0.0168 & 0.6623 & 0.4858 & 0.4474 & 0.3889 & -0.5162 & -0.2902 \\-0.1813 & 0.4428 & -0.2485 & -0.5210 & -0.2160 & 0.2273 & -0.3022 & -0.3756 & 0.1138 & 0.2180 \\0.2345 & -0.3673 & -0.0208 & -0.1335 & 0.1385 & 0.2149 & 0.6787 & -0.7335 & -0.0106 & 0.1181 \\-0.3721 & 0.1472 & -0.3148 & -0.3902 & -0.5528 & -0.3957 & 0.3321 & -0.4586 & 0.0931 & -0.1888 \\0.2077 & -0.1135 & 0.3442 & 0.6898 & 0.2972 & -0.0460 & 0.5437 & 0.3840 & -0.2072 & -0.1516 \\0.3234 & -0.2309 & 0.0452 & -0.1091 & 0.2687 & -0.0085 & 0.3502 & -0.3033 & -0.0314 & 0.0379\end{array}\right] \]

• 掩蔽之后的矩阵

  \[ \left[\begin{array}{cccccccccc} 0.0559 & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty \\ 0.2037 & 0.2918 & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty \\ -0.0866 & -0.7469 & 0.0212 & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty \\ -0.1088 & 0.1867 & -0.3031 & -0.7647 & -\infty & -\infty & -\infty & -\infty & -\infty & -\infty \\ 1.1036 & 0.6895 & 0.4887 & -0.0168 & 0.6623 & -\infty & -\infty & -\infty & -\infty & -\infty \\ -0.1813 & 0.4428 & -0.2485 & -0.5210 & -0.2160 & 0.2273 & -\infty & -\infty & -\infty & -\infty \\ 0.2345 & -0.3673 & -0.0208 & -0.1335 & 0.1385 & 0.2149 & 0.6787 & -\infty & -\infty & -\infty \\ -0.3721 & 0.1472 & -0.3148 & -0.3902 & -0.5528 & -0.3957 & 0.3321 & -0.4586 & -\infty & -\infty \\ 0.2077 & -0.1135 & 0.3442 & 0.6898 & 0.2972 & -0.0460 & 0.5437 & 0.3840 & -0.2072 & -\infty \\ 0.3234 & -0.2309 & 0.0452 & -0.1091 & 0.2687 & -0.0085 & 0.3502 & -0.3033 & -0.0314 & 0.0379 \end{array}\right] \]

关于掩蔽矩阵的讨论

---

我们展示了两个例子，很明显的是，第一个例子的掩蔽是一个上三角矩阵，而第二个掩蔽的例子是一个下三角矩阵。为什么第二个例子才是因果掩蔽呢？我们需要更细致的讨论掩蔽矩阵到底对什么进行了掩蔽。

我们考虑一个例子：

\[ \begin{aligned}Q & =\left[\begin{array}{lllll}1 & 0 & 2 & 0 & 1 \\0 & 1 & 1 & 2 & 0\end{array}\right] ,K & =\left[\begin{array}{lllll}1 & 0 & 1 & 0 & 1 \\0 & 1 & 1 & 1 & 0 \\1 & 1 & 0 & 1 & 0 \\0 & 0 & 1 & 0 & 1\end{array}\right] ,V & =\left[\begin{array}{lllll}1 & 2 & 0 & 0 & 1 \\0 & 1 & 2 & 1 & 0 \\1 & 0 & 1 & 1 & 1 \\2 & 1 & 0 & 2 & 2\end{array}\right]\end{aligned} \]

计算注意力：

\[ \text { Attention Scores }=\left[\begin{array}{llll} 4 & 2 & 1 & 1 \\ 2 & 4 & 2 & 1 \end{array}\right] \]

很显然，两行的注意力得分对应的是两个查询。假设我们希望第一个查询只参考第一个键值对的信息，第二个查询参考前两个键值对的信息。那么我们的掩蔽矩阵应该是：

\[ \text { Mask }=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{array}\right] \]

那么，假设我们有四条查询，对应的因果掩蔽矩阵应该是：

\[ \text { Mask }=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 \end{array}\right] \]

这与本节开始时展示的因果掩蔽的图示正好互为转置。更近一部分，考虑公式：

\[ \operatorname{softmax}\left(\frac{Q K^T}{\sqrt{d_k}}\right) MV \]

中的后两项的矩阵乘积规则，也可以得知对于每一个查询，掩蔽是一个行向量而非列向量。

Encoder Block

---

关于GPT的仅编码器结构

---

在论文《attention is all you need》中，作者绘制了Transformer的结构，这是一种由编码器和解码器组成的结构。在论文《Improving Language Understanding by Generative Pre-Training》，作者也描述了本篇笔记所关注的GPT模型的结构，这是一种仅包含解码器的结构。

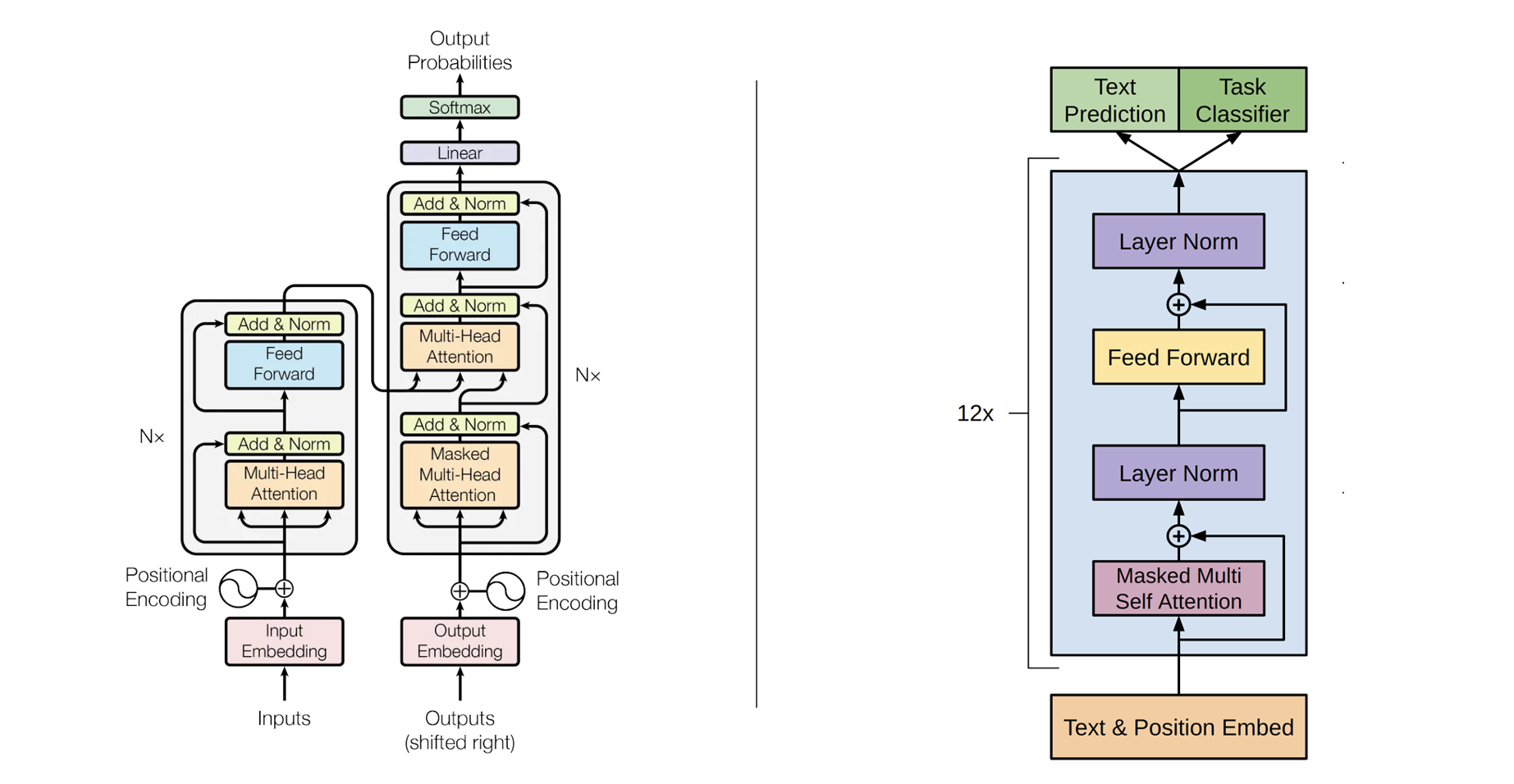
尽管最早的Transformer模型同时具备编码器和解码器，但这并不是必须的。现在的Transformer通常会根据任务类型，选择仅编码器，仅解码器或者编码器-解码器结构。

• 仅编码器结构更适合将文本转化为数字的任务，如分类或者识别等等；
• 仅解码器更适合给定文本提示，如“Thank for lunch， I had a...”，通过迭代预测最可能的下一个单词来自动完成序列的模型，如GPT模型。
• 编码器解码器结构更适合从一个文本序列到另一个文本序列的任务。

Encoder block的结构

---

尽管我们称GPT是一种仅仅包含解码器的结构，但从上图可以看出，其实现中的基本结构与原Transformer模型的编码器结构相同。我们将这种基础结构称为Encoder Block，或者Transfromer Block，或者Encoder layer等等。总之这是一种包含一个多注意力头，两个层归一化层和一组线性神经网络的结构。

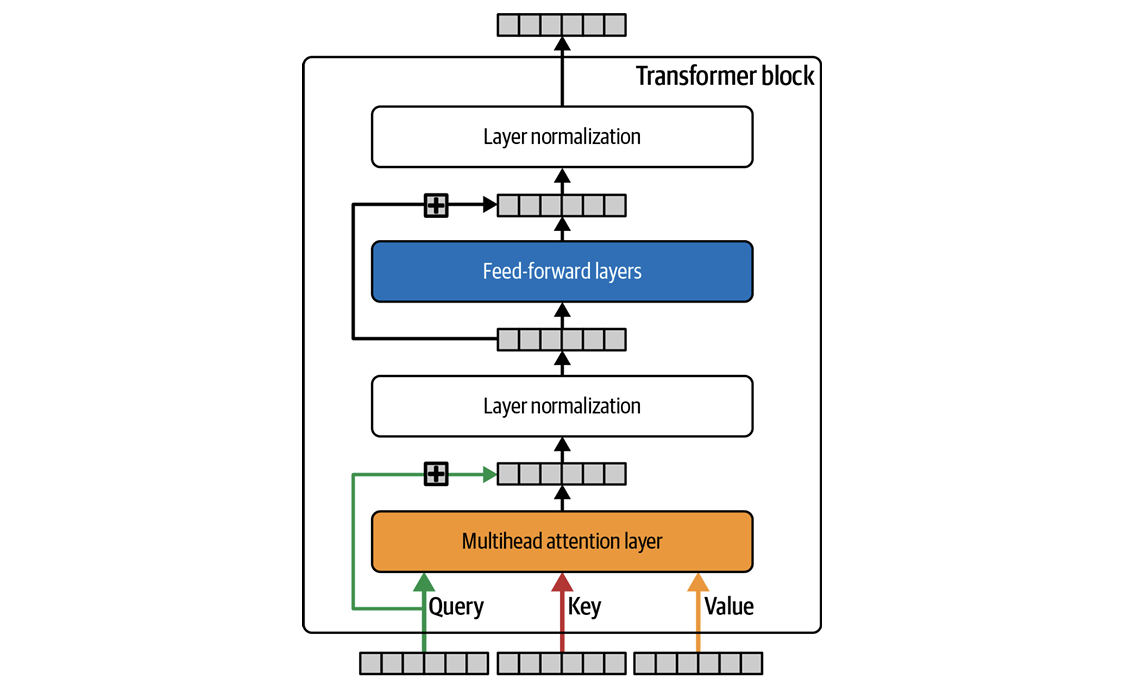
层归一化

---

Transformer结构中通常不使用在其他代码中广为应用的批归一化，以避免在批次内的序列之间产生归一化依赖。但是较新的研究也指出，批归一化的某种形式仍然可以在Transformer中使用，并且在性能上优于传统的层归一化方法。两种归一化方式的区别如下图所示。

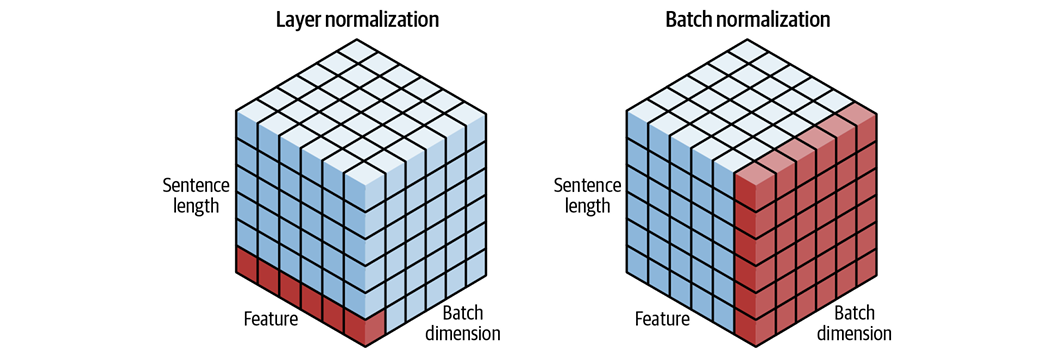
代码实现：encoder block

---

我们已经实现了多注意力，实现encoder block也是十分简单的：

• EncoderBlock

  class EncoderBlock(nn.Module):
      '''
      EncoderBlock 是一个用于 Transformer 架构中的编码器块，结合了多头自注意力机制和前馈神经网络，帮助模型有效捕捉输入序列中不同位置之间的依赖关系。该模块利用了 MultiAttentionHead_B，这是一个支持并行注意力计算的多头注意力机制，通过将输入嵌入向量映射到多个注意力头，再合并输出进行进一步处理。
  
      ### 参数：
      - embed_dim (int)：输入嵌入向量的维度。
      - num_heads (int)：多头自注意力机制中的头数。
      - k_dim (int, 可选)：键（Key）和查询（Query）的维度大小。这个大小必须是 num_heads 的倍数。如果未指定，默认值为 embed_dim。
      - v_dim (int, 可选)：值（Value）的维度大小。这个大小也必须是 num_heads 的倍数。如果未指定，默认值为 embed_dim。
      - hidden_dim (int, 可选)：前馈网络的隐藏层维度。如果未指定，默认值为 embed_dim。
      - qkv_bias (bool, 可选)：是否在生成查询（Query）、键（Key）、值（Value）时使用偏置项，默认值为 False。
      - attn_drop (float, 可选)：多头自注意力机制中的注意力权重的 Dropout 概率，默认值为 0.0。
      - proj_drop (float, 可选)：多头自注意力机制的输出投影的 Dropout 概率，默认值为 0.0。
      - dense_drop (float, 可选)：前馈网络的 Dropout 概率，默认值为 0.0。
      - encoder_norm_layer (nn.Module, 可选)：用于编码器的归一化层类型，默认值为 nn.LayerNorm。
      - attention_norm_layer (nn.Module, 可选)：用于注意力层的归一化层类型，默认值为 nn.LayerNorm。
      - qk_norm (bool, 可选)：是否对查询（Query）和键（Key）进行归一化处理，默认值为 False。仅当 qk_norm=True 时，attention_norm_layer 才会启用。
      - use_fused_attn (bool, 可选)：是否使用 PyTorch 的 scaled_dot_product_attention 函数来加速注意力计算，默认值为 False。
      - is_causal (bool, 可选)：是否启用因果遮掩，用于防止注意力机制关注未来的时间步，默认值为 True。
      - device (str, 可选)：指定模型运行的设备，如 "cpu" 或 "cuda"，默认值为 "cpu"。
      ### 方法：
      - __init__(self, embed_dim, num_heads, ...)
          初始化 EncoderBlock 类，实例化内部的多头注意力机制、前馈神经网络、Dropout 和归一化层。
      - forward(self, x, return_attention=True)
          - 输入：
              - x (Tensor)：输入的嵌入向量，形状为 (batch_size, sequence_length, embed_dim)。
              - return_attention (bool, 可选)：是否返回注意力权重，默认值为 True。
          - 输出：
              - 如果 return_attention=True，返回两项：
                  - result：编码器块的输出，形状为 (batch_size, sequence_length, embed_dim)。
                  - attention：注意力权重的均值，形状为 (batch_size, num_heads, sequence_length, sequence_length)。
                  - 如果 return_attention=False，仅返回 result。
      '''
      def __init__(
          self,
          embed_dim,
          num_heads,
          k_dim=None,
          v_dim=None,
          hidden_dim=None,
          qkv_bias=False,
          attn_drop=0.0,
          proj_drop=0.0,
          dense_drop=0.0,
          encoder_norm_layer=nn.LayerNorm,
          attention_norm_layer=nn.LayerNorm,
          qk_norm=False,
          use_fused_attn=False,
          is_causal=True,
          device="cpu",
      ):
          super().__init__()
          self.embed_dim = embed_dim
          self.num_heads = num_heads
          self.k_dim = k_dim if k_dim is not None else embed_dim
          self.v_dim = v_dim if v_dim is not None else embed_dim
          self.hidden_dim = hidden_dim if hidden_dim is not None else embed_dim
          self.attn_drop = attn_drop
          self.proj_drop = proj_drop
          self.dense_drop = dense_drop
          self.qk_norm = qk_norm
          self.qkv_bias = qkv_bias
          self.encoder_norm_layer = encoder_norm_layer
          self.attention_norm_layer = attention_norm_layer
          self.use_fused_attn = use_fused_attn
          self.device = device
  
          self.attn = MultiAttentionHead_A(
              embed_dim=self.embed_dim,
              num_heads=self.num_heads,
              k_dim=self.k_dim,
              v_dim=self.v_dim,
              out_proj=True,
              qkv_bias=self.qkv_bias,
              attn_drop=self.attn_drop,
              proj_drop=self.proj_drop,
              qk_norm=self.qk_norm,
              norm_layer=self.attention_norm_layer,
              use_fused_attn=self.use_fused_attn,
              device=self.device,
              is_causal=is_causal,
          )
          # self.attn = nn.MultiheadAttention(
          #     embed_dim=self.embed_dim,
          #     num_heads=self.num_heads,
          #     kdim=self.k_dim,
          #     vdim=self.v_dim,
          #     dropout=self.attn_drop,
          #     add_zero_attn=False,
          #     bias=self.qkv_bias,
          #     batch_first=True,
          #     device=self.device,
          # )        
          self.dropout1 = nn.Dropout(self.dense_drop)
          self.lnorm1 = self.encoder_norm_layer(self.embed_dim)
          self.linear1 = nn.Linear(self.embed_dim, self.hidden_dim)
          self.ReLU = nn.ReLU()
          self.linear2 = nn.Linear(self.hidden_dim, self.embed_dim)
          self.dropout2 = nn.Dropout(self.dense_drop)
          self.lnorm2 = self.encoder_norm_layer(self.embed_dim)
          self.dropout3 = nn.Dropout(self.dense_drop)
          self.to(self.device)
  
      def forward(self, x, return_attention=False):
          seq_len = x.size(1)
          mask = torch.triu(torch.ones(seq_len, seq_len), diagonal=1).bool().to(x.device)
          result, attention = self.attn(x, x, x, mask=None, return_attention=True)
          # result, attention = self.attn(x, x, x, need_weights=True, attn_mask=mask)
          result = self.dropout1(result)
          result = x + result
          result = self.lnorm1(result)
          x = result
          result = self.linear1(result)
          result = self.ReLU(result)
          result = self.dropout2(result)
          result = self.linear2(result)
          result = self.dropout3(result)
          result = self.lnorm2(result + x)
          if return_attention and attention is not None:
              return result, torch.mean(attention, dim=1)
          elif return_attention:
              return result, None
          return result

在实现之后可以测试代码：

encoder_block = EncoderBlock(  embed_dim=512,  num_heads=8,  k_dim=64,  v_dim=64,  hidden_dim=2048,  qkv_bias=False,  attn_drop=0.0,  proj_drop=0.0,  dense_drop=0.0,  encoder_norm_layer=nn.LayerNorm,  attention_norm_layer=nn.LayerNorm,  qk_norm=False,  use_fused_attn=False,  is_causal=True,  device="cpu",)
x = torch.randn(1, 10, 512)
result, attention = encoder_block(x)
print(result.shape)
print(attention.shape)
---
torch.Size([1, 10, 512])
torch.Size([1, 10, 10])

值得注意的是，在此程序的forward中增加了return_attention 参数，以返回每组键值对得到的权重。这依赖于之前一直没有讨论的多注意力forward的return_attention 参数。这个参数是可选的，大部分时候我们都并不需要这一项。

---

使用nn.TransformerEncoderLayer和nn.TransformerEncoder实现

使用类似如下的方式可以实现相同的encoderblock

transformer_layer = nn.TransformerEncoderLayer(
  d_model=embedding_dim, 
  nhead=num_heads, 
  dim_feedforward=feed_forward_dim,
  batch_first=True
)
self.transformer = nn.TransformerEncoder(transformer_layer, num_layers=num_layers)

更多的参数和使用方式可以参照官方文档。

GPT模型

---

GPT模型的构建

---

GPT模型的基础结构如下：

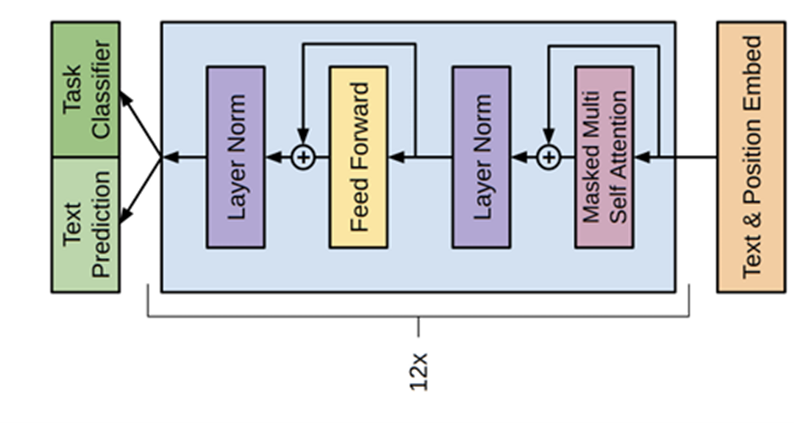
模型中包括12个encoder block。数据经过字符编码和位置编码之后，输入encoder block种，然后根据不同的任务输入不同的头中。

---

尝试实现GPT模型，此模型包含一个预测任务的任务头，即那个线性层。

• GPT

  class GPT(nn.Module):
      def __init__(
          self,
          vocab_size,
          embed_dim,
          num_heads,
          num_layers,
          max_len,
          feed_forward_dim = None,
          device="cpu",
          use_fused_attn=True,
      ):
          super(GPT, self).__init__()
          self.vocab_size = vocab_size
          self.embed_dim = embed_dim
          self.num_heads = num_heads
          self.num_layers = num_layers
          self.max_len = max_len
          self.device = device
          feed_forward_dim = embed_dim if feed_forward_dim is None else feed_forward_dim
  
          self.token_embedding = nn.Embedding(vocab_size, embed_dim)
          self.position_embedding = nn.Embedding(max_len, embed_dim)
          self.encoder_blocks = nn.ModuleList(
              [
                  EncoderBlock(embed_dim, num_heads, device=device, use_fused_attn=True)
                  for _ in range(num_layers)
              ]
          )
  
          self.linear = nn.Linear(embed_dim, vocab_size)
          self.softmax = nn.Softmax(dim=-1)
          self.to(device)
  
      def forward(self, x, return_attention=False):
          seq_len = x.size(1)
          positions = torch.arange(0, seq_len, device=x.device).unsqueeze(0)
          token_embeddings = self.token_embedding(x)
          position_embeddings = self.position_embedding(positions)
          x = token_embeddings + position_embeddings
          attentions = []
          for encoder_block in self.encoder_blocks:
              x, attention = encoder_block(x, return_attention=True)
              attentions.append(attention)
          x = self.linear(x)
          if return_attention:
              return x, attentions
          return x

假设输入的尺寸为\(x(batchsize,len)\)，那么输出的尺寸为\(y(batchsize,len,vocabsize)\)，其中\(vocabsize\)是词汇表尺寸，即最终输出是一个词汇表大小的概率分布，即词汇表中每个词成为下一个词的可能的概率。

在使用pytorch的encoderblock时，需注意因果掩蔽的实现方式。

GPT模型的预训练

---

GPT模型，如期所称，是一种生成式预训练模型。预训练过程中，我们关注模型“理解文本”的能力。具体来时，我们希望最大化如下似然函数：

\[ L_1(U)=\sum_i \log P\left(u_i \mid u_{i-k}, \ldots, u_{i-1} ; \Theta\right) \]

其中，

• \(k\) 表示上下文窗口的大小，到目前为止我们默认这一项为文本长度。
• \(P\) 是条件概率，由带参数 \(\Theta\) 的神经网络建模。
• 参数 \(\Theta\) 通过随机梯度下降 (Stochastic Gradient Descent, SGD) 进行训练。

及我们希望通过随机梯度下降，调整神经网络参数，以使其在已知现有信息的情况下，推测下一个信息。即在第二节中的开始展示的游戏。

我们使用Adam优化器，原文同时使用了学习率在最初的2000次更新中从零线性增加，并随后使用余弦调度（cosine schedule）逐步衰减至0的学习率更新策略，可以使用如下的代码实现：

optimizer = torch.optim.Adam(model.parameters(), lr=LEARNING_RATE)  # 初始学习率为0
TOTAL_STEPS = len(train_loader) * EPOCHS
WARMUP_STEPS = TOTAL_STEPS // 5
# 定义学习率调度策略
def lr_lambda(current_step):
    if current_step < WARMUP_STEPS:
        return current_step / WARMUP_STEPS
    else:
        return 0.5 * (
            1
            + torch.cos(
                (current_step - WARMUP_STEPS) / (TOTAL_STEPS - WARMUP_STEPS) * torch.pi
            )
        )  # 余弦调度

# 创建学习率调度器
scheduler = LambdaLR(optimizer, lr_lambda)

# 训练循环
for epoch in range(EPOCHS):
    model.train()
    for idx, (x, y) in enumerate(train_loader):
        x, y = x.to(device), y.to(device)
        optimizer.zero_grad()
        output = model(x)
        loss = criterion(output.view(-1, VOCAB_SIZE), y.view(-1))
        loss.backward()
        optimizer.step()
        scheduler.step()
        if idx % 100 == 0:
            print(
                f"Epoch: {epoch}, Step: {idx}, Loss: {loss.item() / BATCH_SIZE}, LR: {scheduler.get_last_lr()[0]}"
            )

此外，预训练任务的结果与分类任务十分相似。最终的向量是一个长度为vocab_size 的张量，而目标值为一个长度为vocab_size 的one-hot编码。因此我们使用交叉熵函数作为损失函数。

criterion = nn.CrossEntropyLoss()

GPT模型的预训练结果测试

---

预训练模型根据所有已经获得的知识预测下一个单词，因此可以直接向它提供一个开头，指定最大长度和温度，使其完成续写。

def generate_text(model, start_token, max_len, device, temperature=1.0):
    model.eval()
    generated_tokens = [start_token]
    input_tensor = torch.tensor([generated_tokens], dtype=torch.long, device=device)

    with torch.no_grad():
        for _ in range(max_len - 1):
            outputs = model(input_tensor)
            next_token_logits = outputs[0, -1, :]
            next_token_logits = next_token_logits / temperature
            next_token_probs = F.softmax(next_token_logits, dim=-1)
            next_token = torch.multinomial(next_token_probs, num_samples=1).item()
            generated_tokens.append(next_token)
            input_tensor = torch.tensor(
                [generated_tokens], dtype=torch.long, device=device
            )
    return generated_tokens

在这个函数中，temperature只影响随机选择时的概率。

关于在模型中只指定一部分参数参加训练

---

使用 requires_grad 设置梯度计算开关

对不希望训练的参数，将其属性 requires_grad 设置为 False。在这种情况下，这些参数的梯度不会被计算，也不会参与优化。

import torch
import torch.nn as nn

# 示例模型
class MyModel(nn.Module):
    def __init__(self):
        super(MyModel, self).__init__()
        self.trainable_layer = nn.Linear(10, 10)
        self.frozen_layer = nn.Linear(10, 5)

    def forward(self, x):
        x = self.trainable_layer(x)
        x = self.frozen_layer(x)
        return x

# 实例化模型
model = MyModel()

# 冻结 frozen_layer 的参数
for param in model.frozen_layer.parameters():
    param.requires_grad = False

# 检查 requires_grad 状态
for name, param in model.named_parameters():
    print(f"{name}: requires_grad={param.requires_grad}")

在优化器中仅添加需要训练的参数

只将 requires_grad=True 的参数添加到优化器中。

optimizer = torch.optim.Adam(filter(lambda p: p.requires_grad, model.parameters()), lr=0.001

手动指定参数组

可以在定义优化器时手动划分参数组。例如，某些层的参数使用一个学习率，其他层则冻结。

optimizer = torch.optim.Adam([
    {'params': model.trainable_layer.parameters()},  # 参与训练的参数
    {'params': model.frozen_layer.parameters(), 'lr': 0.0}  # 不参与训练的参数
], lr=0.001)

使GPT模型应用于不同的任务

---

除了我们在预训练时使用的预测任务之外，还可以进行多种语言相关的任务。为此，我们希望在预训练之后，保存gpt模型的一部分不再改动，而是仅训练任务头，即finetune。

为此，稍微修改gpt模型以实现在pretrain时训练gpt模型，并在finetune时训练任务头。

class GPT(nn.Module):
    def __init__(
        self,
        vocab_size,
        embed_dim,
        num_heads,
        num_layers,
        max_len,
        feed_forward_dim = None,
        device="cpu",
        use_fused_attn=True,
    ):
        super(GPT, self).__init__()
        self.vocab_size = vocab_size
        self.embed_dim = embed_dim
        self.num_heads = num_heads
        self.num_layers = num_layers
        self.max_len = max_len
        self.device = device
        feed_forward_dim = embed_dim if feed_forward_dim is None else feed_forward_dim

        self.token_embedding = nn.Embedding(vocab_size, embed_dim)
        self.position_embedding = nn.Embedding(max_len, embed_dim)
        self.encoder_blocks = nn.ModuleList(
            [
                EncoderBlock(embed_dim, num_heads, device=device, use_fused_attn=True)
                for _ in range(num_layers)
            ]
        )

        self.linear = nn.Linear(embed_dim, vocab_size)
        self.softmax = nn.Softmax(dim=-1)
        self.to(device)

    def forward(self, x, return_attention=False):
        seq_len = x.size(1)
        positions = torch.arange(0, seq_len, device=x.device).unsqueeze(0)
        token_embeddings = self.token_embedding(x)
        position_embeddings = self.position_embedding(positions)
        x = token_embeddings + position_embeddings
        attentions = []
        for encoder_block in self.encoder_blocks:
            x, attention = encoder_block(x, return_attention=True)
            attentions.append(attention)
        # x = self.linear(x)
        if return_attention:
            return x, attentions
        return x
    
class TaskHead(nn.Module):
    def __init__(self, embed_dim, num_classes, device='cpu'):
        '''
        num_classes: int, number of classes, if task is 'classification', num_classes is the number of classes, if task is 'prediction', num_classes is the size of vocabulary
        '''
        super(TaskHead, self).__init__()
        self.num_classes = num_classes
        self.linear = nn.Linear(embed_dim, num_classes)
        self.softmax = nn.Softmax(dim=-1)
        self.to(device)

    def forward(self, x):
        x = self.linear(x)
        x = self.softmax(x)
        return x

class GPT_AT(nn.Module):
    def __init__(self, gpt, task_head, mode = 'pretrain'):
        '''
        mode: str, 'pretrain' or 'finetune'
        '''
        super(GPT_AT, self).__init__()
        self.mode = mode
        self.gpt = gpt
        self.task_head = task_head
        
        if self.mode == 'finetune':
            self.gpt.requires_grad = False
    def forward(self, x):
        x = self.gpt(x)
        x = self.task_head(x)
        return x
    def return_module(self, module_name):
        return self.gpt, self.task_head