TS02 Localisation de Source
TS02 Localisation de Source
I 建模
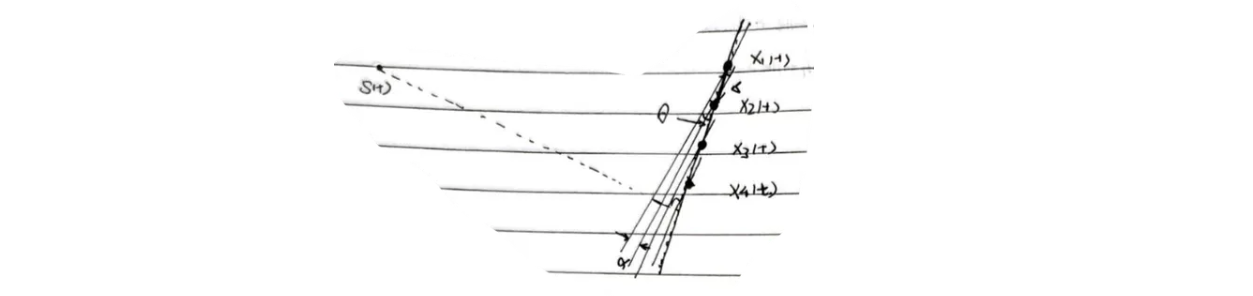
假设声源发射信号为:\(S(t)=\alpha e^{i 2 \pi f_0 t}\)
不同麦克风接收到的信号即为:\(x_{n}=\gamma_n S\left(t-\tau_n\right)+b(t)\)
- 其中,\(\tau_n-\tau_{n-1} = \Delta \tau = \alpha/c = \Delta sin(\theta)/c\),其中,\(\Delta\)为麦克风之间的距离,\(\theta\)为垂直声波梯度方向与麦克风阵列所在直线的夹角。
假设\(\alpha\)是一个常数或者一个可确定的参数,接收到的信号为:
\[ x_n=\gamma_n \alpha e^{i 2 \pi f_0 (t-t_0)} e^{-i 2 \pi f_0 (N-1)\Delta \tau}=\gamma_n \alpha e^{i 2 \pi f_0 t} e^{-i 2 \pi f_0 d_n/c} \]
其中,\(d_n\)是麦克风到扬声器的的距离\(d_n = \|P_s-P_n\|\)。
频域模型
在频域下,有\(\tilde{x}_n(f)=A g_n+\tilde{b}(f)\)。测量值:
\[ \mathbf{m}=\left[\begin{array}{c}\tilde{x}_1\left(f_0\right) \\\tilde{x}_2\left(f_0\right) \\\vdots \\\tilde{x}_n\left(f_0\right)\end{array}\right]=A g\left(f_0\right)+\tilde{b} \]
II 最大似然估计
根据以上的推测,在实际计算中我们需要从观测数据中推测\(\theta\)或\(P_s\)等某些参数。假设观测信号的分布为高斯分布,其概率密度函数为:
\[ f_m(\theta)=\frac{1}{\pi^N \sigma^{2N}} e^{-\frac{\left\|m-A g\left(P_s,\theta \right)\right\|^2}{\sigma^2}} \]
其似然函数:
\[ L(\theta)=\log f_m(\theta)=-\frac{\left\|m-A g\left(P_s,\theta\right)\right\|^2}{\sigma^2}+\text { const. } \]
因此最大化似然即为最小化\(\left\|m-A g\left(P_s, \theta\right)\right\|^2\)。
如果忽略
III 远场模型和频率选择
在远场假设和均匀线性假设得前提下,有:
\[ g_n(\theta) = e^{-i2\pi f_0\tau_n} = e^{-i 2 \pi \Delta sin(\theta)(n-1)/\lambda} \]
此时,在测量时角度为\(\theta_0\)\(m\)为:
\[ m_{\theta_0}= A\left[\begin{array}{l}1 \\e^{-i 2 \pi \frac{\Delta \sin \theta_0}{\lambda}} \\e^{-i 2 \pi \frac{\Delta \sin \theta_0}{A}(N -1)}\end{array}\right]+b \]
我们应用最大似然估计,即选择能使\(B(\theta) = |<m,\frac{g(\theta)}{\|g(x)\|^2}>|^2\)最大的\(\theta\)作为我们的估计值,即:
\[ \theta_e = argmax( |<m,\frac{g(\theta)}{\|g(x)\|^2}>|^2) \]
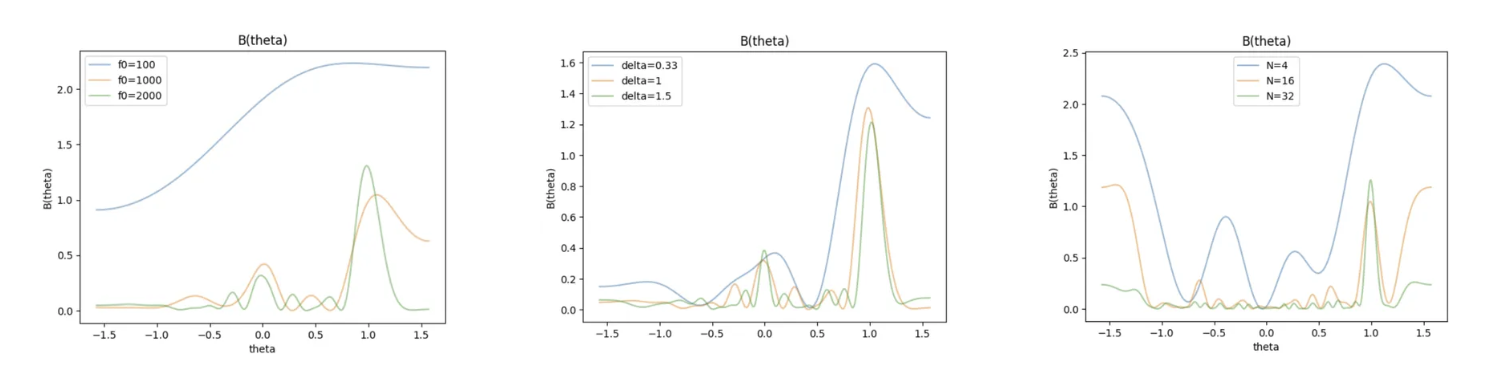
在这一过程中,参数\(f_0,\Delta\)和\(N\)都会有影响。三者的增大均有利于更准确的结果,但并非能无限制的增大。
频率选择
在传播过程中,有相对相位:
\[ z=\frac{\Delta \sin \theta}{\lambda} \]
为了避免混叠,要求相对相位在\(\left[-\frac{1}{2}, \frac{1}{2}\right]\)范围之内。因此有:
\[ \frac{\Delta sin(\theta)}{\lambda}<1/2\Rightarrow\Delta<\frac{\lambda}{2} = \frac{c}{2f_0} \]
III 近场模型和测量
与远场模型不同,近场模型的传播被表示为:
\[ g(f(s))=\left[\begin{array}{c}\frac{1}{d_1} e^{-i 2 \pi f_0 \frac{d_1}{c}} \\\ldots \\\frac{1}{d_n} e^{-i 2 \pi f_0 \frac{d_n}{c}}\end{array}\right] \]
除此之外在处理上与远场模型并没有太大的区别。
这里我们着稍微讨论一下在测量方法。
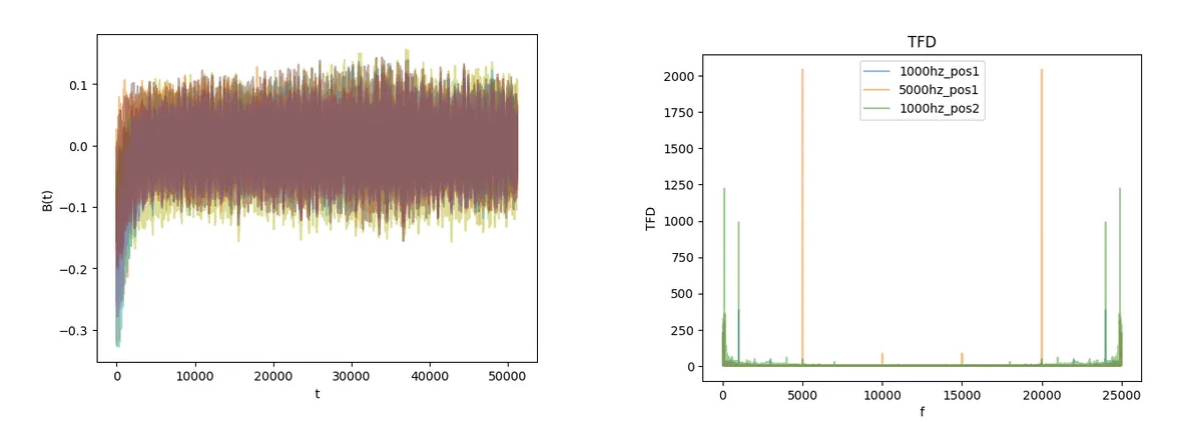
通常在采集完成之后,我们得到一个\(N\times L\)的信号,\(N\)为麦克风数量,\(L\)为采样点数。我们进行傅里叶变换,得到一个新的\(N\times L\)的矩阵。选择第\(K_0 = Lf_0/f_{sample}\)列,即为\(m\)。


