TS01 Réponse Impulsionnelle de Salle

I. 建模 Modèle

\[ y(h) = \sum_{i=1}^K K_i \cdot x(h - \tau_i) \]

其中：

  • \(y(t)\)是接受信号
  • \(K_i\)是不同路径的增益
  • \(\tau_i\)是不同路径的延迟

系统脉冲响应

\[ y(t)=\sum_{i=1}^K \alpha_i\left(x * \delta \tau_i\right)(t)=x+\underbrace{\sum_{i=1}^K \alpha_i\delta \tau_i(t)}_{h(t)} \]

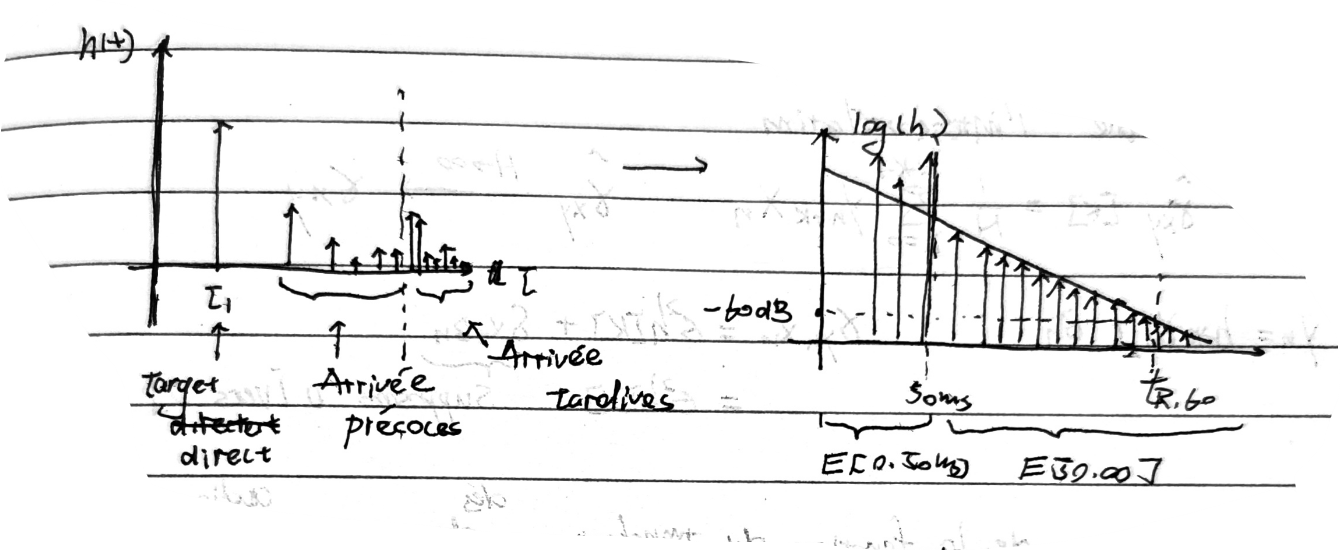
  • 时间响应 \(h(t)\)：
    • 直接路径：\(\tau_i\)
    • 回声：早到 précoces 与迟到 tardives

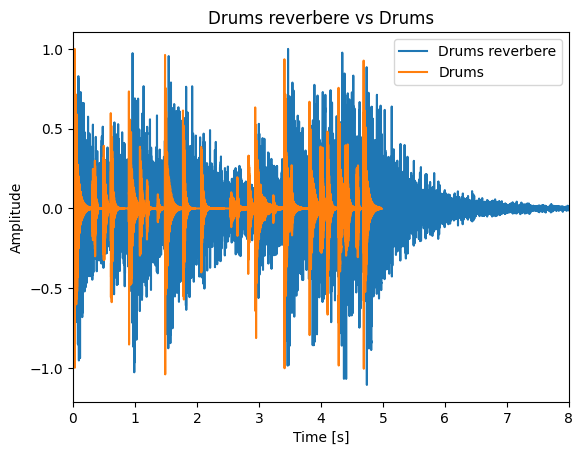
代码的模拟

1
drums_reverbere = np.convolve(drums_resample, sportscentre_resample, mode='full')

清晰度clarité

\[ C_{50}=\frac{E[0,50 \mathrm{~ms}]}{E[50 \mathrm{ms} , \infty ]}=10 \log _{10}\left(\frac{E[0,50 \mathrm{~m}]}{E[50 \mathrm{ms} ,\infty]}\right) \mathrm{dB} \]

  • \(C_{50} > 20 \ \text{dB}\) （适用于语言）
  • \(-6dB<C_{80}<6dB\) （适用于音乐）

II. 脉冲源的测量原理 Principe de Mesure avec Source d’Impulsion

  • 发射信号 \(x(t)= A \cdot \delta (t)\)
  • 接受信号

\[ y(t)=x * h(t)+b(t) =A h(t)+b(t) \]

  • 限制条件：
    • \(SNR = \frac{S}{E}\)
    • \(x(t)\)不是严格意义上的脉冲信号

III. 白噪音原的测量 Mesure avec une Source de Bruit Blanc

  • 接受信号

    \[ y_n=h_* x_n=\sum_k h_k{ } x_{n-k} \]

  • \(x_n\)是白噪音

    \[ E\left\{X_n\right\}=0\\\gamma_x[k]=E\left[x_n x_{n-k}\right]=\sigma_x^2 \delta_0[x] . \]

  • 接受信号和发送信号的互相关

\[ \begin{aligned}\gamma_{y x}[k] & =E\left(y_n x_{n-k}\right)=E\left(\sum_i h[i] X_{n-i} \cdot X_{n-k}\right) \\& =\sum_z h[i] E\left(X_{n-i} X_{n-k}\right)=\sum_i h[i] \sigma_x^2 \delta[i-k] \\& =\sigma_x^2 h[k]\end{aligned} \]

  • 互相关的估计

\[ \hat{\gamma}_{x y}[k]=\frac{1}{N} \sum_{n=0}^{N-1} y_{n+k} x_n \quad \hat{\gamma}_{x y} \xrightarrow{N \rightarrow \infty} \gamma_{x y} \]

  • 有噪音情况下的互相关估计

\[ \begin{aligned} y_n=&h * x_n+B_n , \ \gamma_{y_n x_n}=\sigma^2 h[k]+\delta x_n B_n \\ =&\sigma^2h[k] \end{aligned} \]

1
h = 1/bruit_blanc_reverbere.shape[0]*sig.correlate(bruit_blanc_reverbere, bruit_blanc, mode='valid')

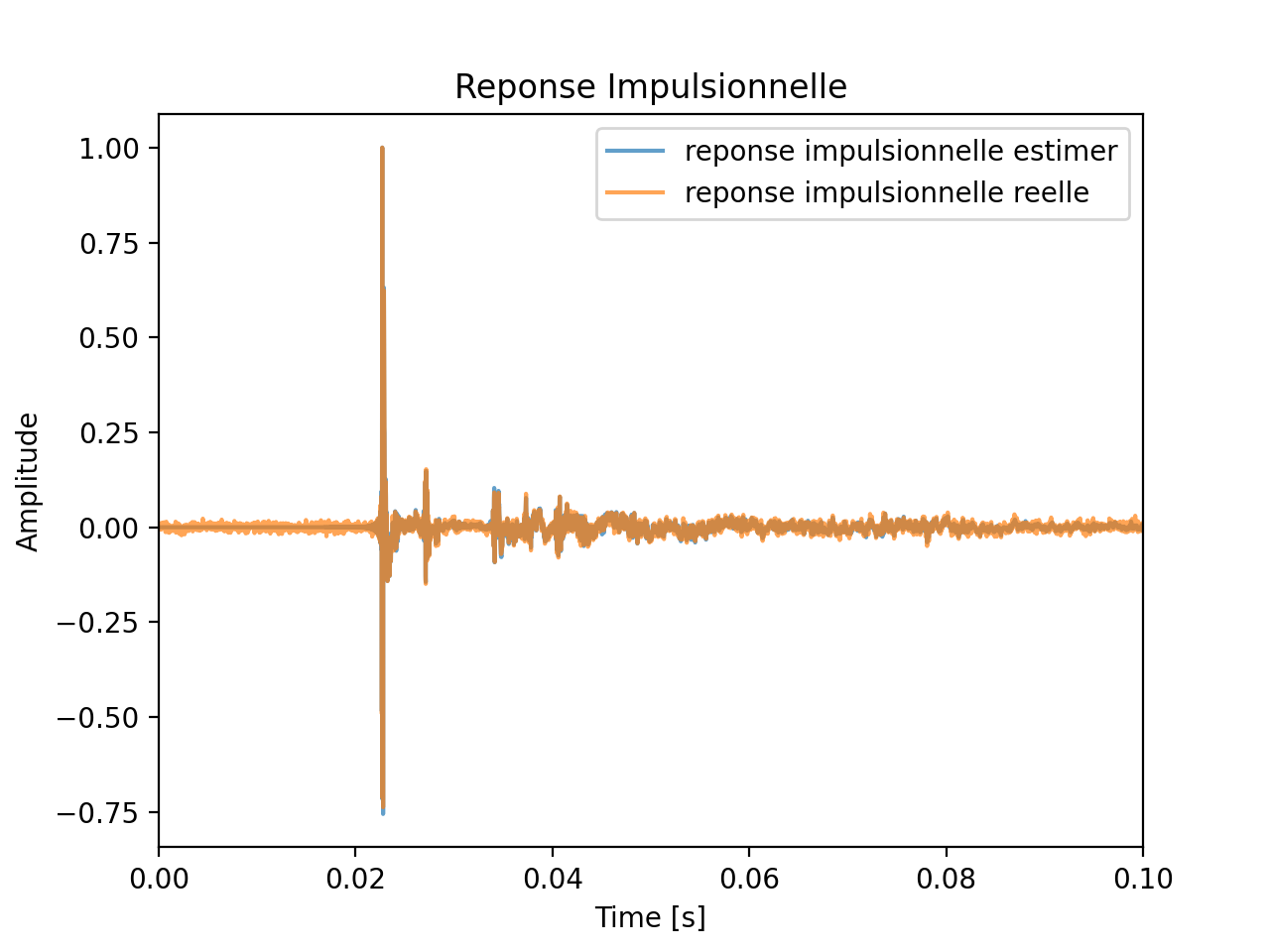
IV. 音频系统传递函数的影响 Influence de la Fonction du Transfert sur des Systèmes Audio

\[ \begin{aligned}&y(t)=\underbrace{\left(h_{\text {Hp }} * h_{\text {salle }} * h_{\text {micro }}\right)} * x(t)) \\& h=h_{\text {salle }} *\left(h_{\text {Hp }} * h_{\text {micro }}\right) \\&=h_{\text {salle }} * h_{\text {systeme }}\end{aligned} \]

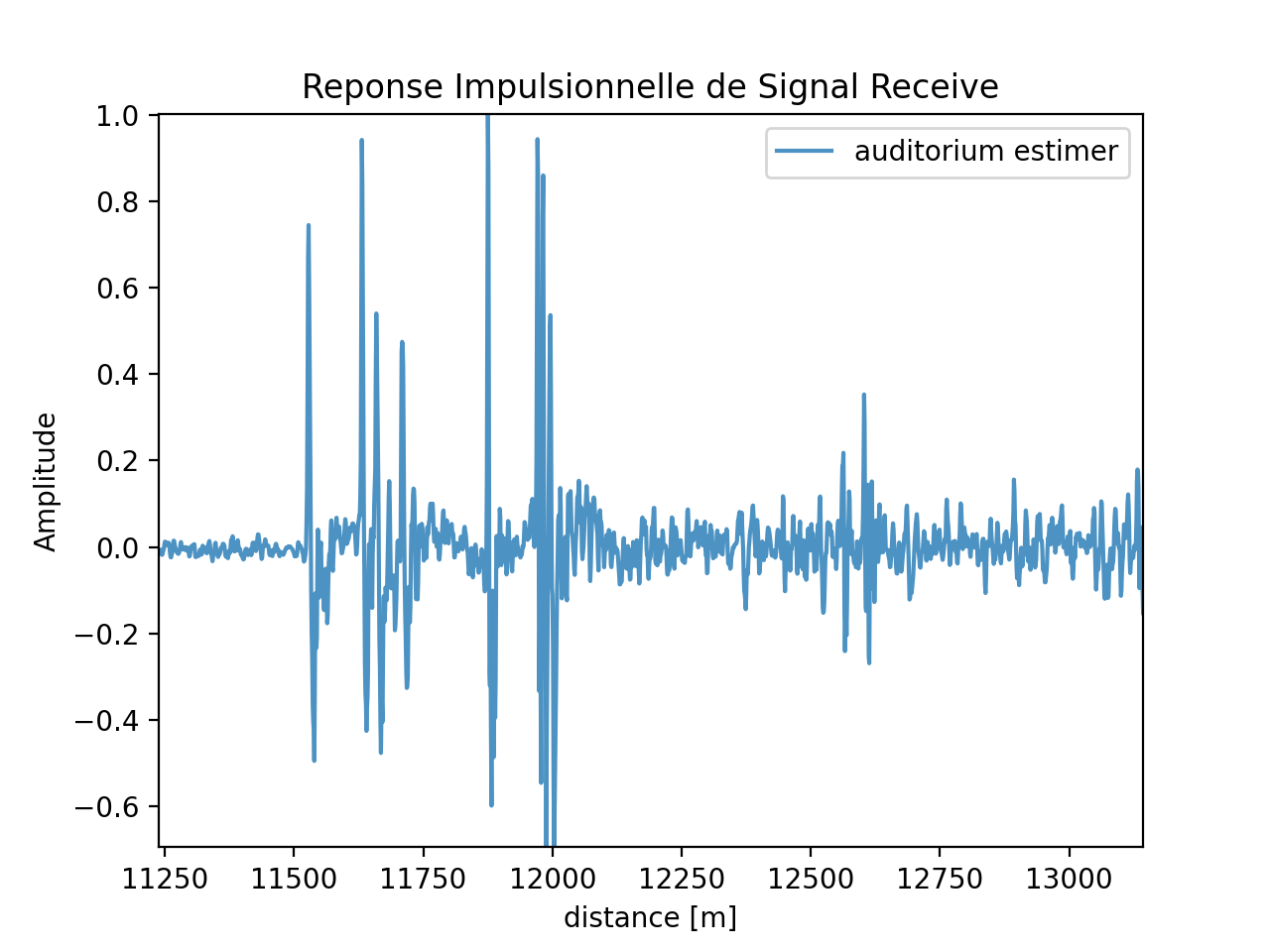
去卷积（Deconvolution）

  • Approche 1

    \[ \begin{aligned}& H(f)=H_{\text {salle}}(f) \times H_{\text {sys}}(f) \\& \Rightarrow H_{\text {salle }}(f)=\frac{H(f)}{H_{\text {sys}}(f)}\end{aligned} \]

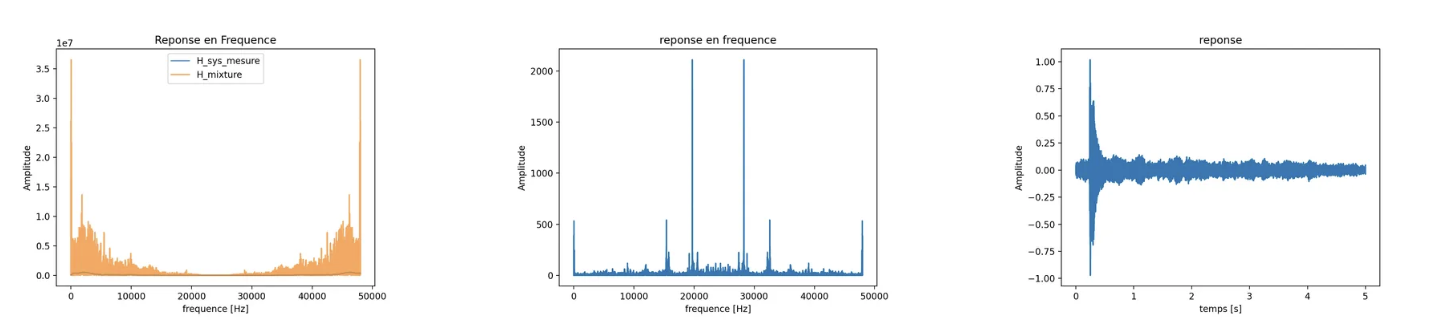
  • Approche 2

\[ \begin{aligned}& J_{h _{salle}}=\| h-h_{salle } * h_{audio}\left\|_2^2+\lambda\right\| h_{salle}\| \\& h_{salle}=\operatorname{argmin} J_{h_{salle}} \end{aligned} \]

补充

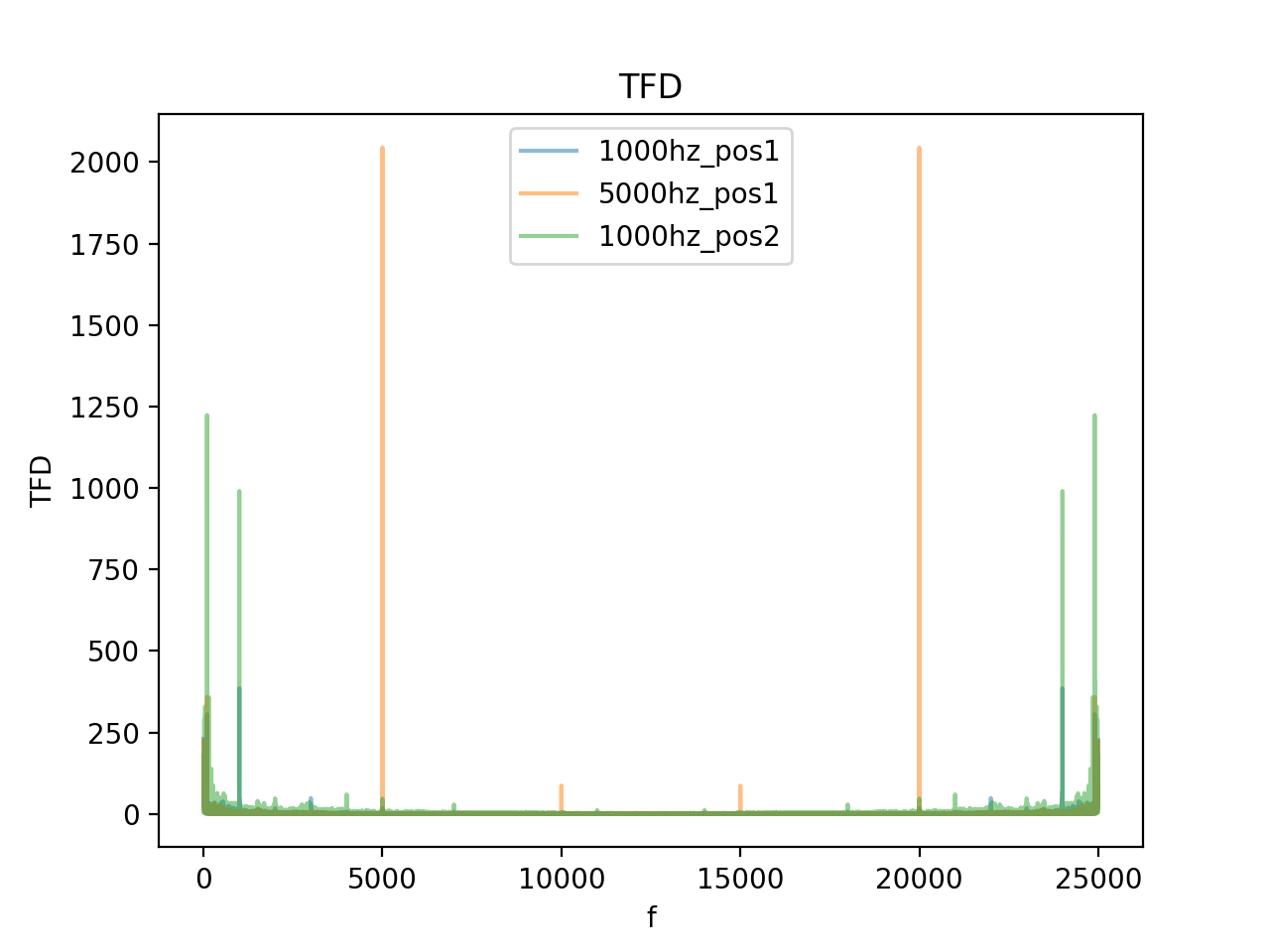
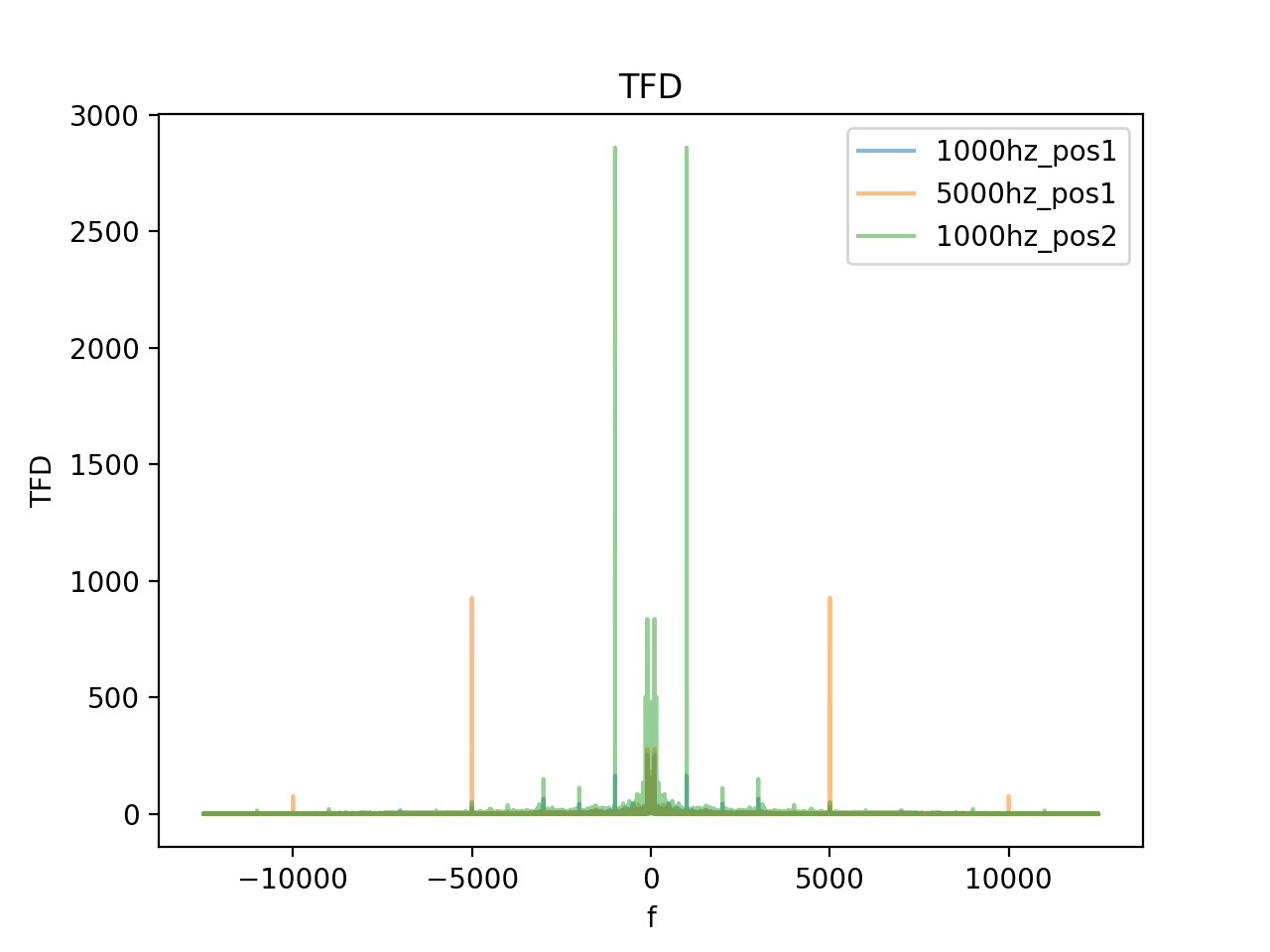
关于np.fft.fft 和np.fft.fftshift ，前者用于计算傅里叶变换，计算完之后的频率分布为[0，正频率，负频率]；后者用于移动0点到坐标轴的中心，变为[负频率，0，正频率]。