Chap2：市场与监管 Marchés et Régulations

欧洲的竞争 Le concurrence en Europe

竞争和监管

欧盟的经济目标：在可能的地方推广竞争 mettre en place la concurrence partout où cela est possible

历史上垄断的多个领域向竞争开放
对消费者的预期收益：价格更低、产品更多样化等produits moins chers, plus de variété
对企业的预期收益：规模经济、成本下降、利润增加 économies d’échelle, baisse des coûts, augmentation des profits

竞争是经济系统的理想状态。

监管Régulation的其他形式

欧盟委员会加强对非法合谋的监督
同时构建新的“自然垄断”...
还有环境政策，如“外部性的内部化”等

需求供给曲线

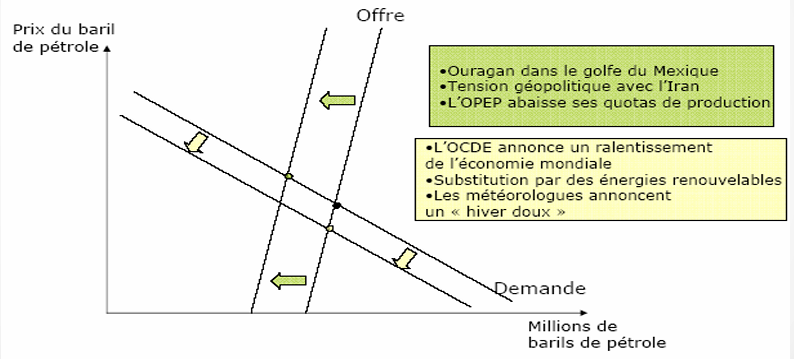
纵轴：石油的价格（每桶价格）。
横轴：石油的数量（百万桶）。
供给曲线（offre）：向右上倾斜，表示随着价格上升，供应量增加。
需求曲线（demande）：向右下倾斜，表示随着价格上升，需求量减少。

供给减少（曲线左移）

墨西哥湾的飓风：自然灾害会减少生产能力，导致供给减少。
与伊朗的地缘政治紧张局势：政治冲突可能阻碍石油生产或运输，导致供给减少。
OPEC（石油输出国组织）降低生产配额：通过限制生产量，OPEC控制供给减少，推动价格上涨。、

需求减少（曲线左移）

经济合作与发展组织（OECD）宣布全球经济放缓：经济放缓通常会导致能源需求减少。
替代能源的使用增加：可再生能源的使用上升，减少了对石油的需求。
气象预报预测暖冬：温和的冬季会减少对取暖用能源的需求。

供给曲线和需求曲线

供给曲线是整个行业中所有企业个体供给曲线的汇总。
需求曲线是不同消费者个体需求曲线的汇总。

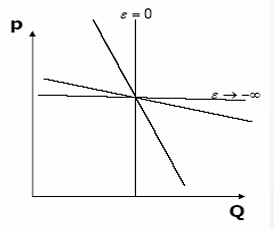
需求价格弹性 élasticité-prix de la demande

需求价格弹性定义如下：

当 \(ε=0\) 时，需求是完全无弹性totalement inélastique的。
当 \(∣ε∣<1\) 时，需求是低弹性faiblement élastique的。
当 \(∣ε∣>1\) 时，需求是有弹性的élastique。

短期与长期 à court terme et long terme

短期，需求的弹性较小（需求对价格变化反应较弱）。
长期，是指所有对价格变化的调整完成所需的时间，此时需求弹性较大（消费者有更多时间调整，需求对价格变化反应更强）。

交叉价格弹性和收入弹性

需求的交叉价格弹性：

\[ \varepsilon_{i j}=\frac{d Q_i / Q_i}{d p_j / p_j}=\frac{d Q_i}{d p_j} \frac{p_j}{Q_i} \]
- 如果 \(\varepsilon_{i j}>0\) ，商品 \(i\) 和商品 \(j\) 是可替代的 substituables。
- 如果 \(\varepsilon_{i j}<0\) ，商品 \(i\) 和商品 \(j\) 是互补的complémentaires。
需求的收入弹性

\[ \varepsilon_R=\frac{d Q / Q}{d R / R}=\frac{d Q}{d R} \frac{R}{Q} \]
- 如果 \(\varepsilon_R>1\) ，该商品被称为奢侈品。
- 如果 \(\varepsilon_R<0\) ，该商品被称为低档品。
其中，\(Q\) 表示商品的需求量（quantity demanded）。
\(p\) 表示商品的价格（price）。
\(R\) 表示消费者的收入（income）。

大类商品	需求收入弹性	具体商品	需求收入弹性
烟草	-0.50	煤炭	-2.02
燃料与照明	0.30	面包和谷物	-0.50
食品	0.45	乳制品	0.53
酒精饮料	1.14	蔬菜	0.87
服装	1.23	海外旅行	1.14
耐用消费品	1.47	娱乐商品	1.99
服务	1.75	葡萄酒与烈酒	2.60

企业的技术 technologie de l’entreprise

企业的生产条件 Les conditions de production de l’entreprise

企业通过使用生产要素 facteurs de production 来进行生产：
- 资本 (K，capital) 和劳动 (L，travail)
生产函数 La fonction de production：
- 表示在给定生产要素数量下的产出数量：\(Q = F(K, L)\)
生产函数的特性：
- 生产函数是递增和凹的。
- 边际收益递减 les rendements marginaux sont décroissants：\(F'_K > 0，F'_L > 0，F''_K < 0，F''_L < 0\)
  - 即生产要素的边际贡献递减，意味着使用的生产要素越多，其贡献效率逐渐降低。
生产要素的成本 coût：
- 劳动的成本是工时数，资本的成本是机器使用的小时数。
- 工资率 (w)：每小时的工资 taux de salaire horaire。
- 资本成本率 (r)：每小时的资本成本 coût horaire du capital。

企业的成本函数 La fonction de coûts de l'entreprise

固定成本 (CF, Coût fixe)：恒定的费用。
可变成本 (CV(Q), coût variable)：随产量 (Q) 变化的成本。
总成本函数 (CT(Q), Fonction de coût total)：
- 公式：CT(Q) = CF + CV(Q)
平均成本函数 (CM(Q), Fonction de coût moyen)：
- 公式：CM(Q) = CT(Q) / Q = CF / Q + CV(Q) / Q
边际成本函数 (Cm(Q), Fonction de coût margina)：
- 公式：Cm(Q) = CT'(Q) = CV'(Q)

完美竞争 concurrence parfaite

完全竞争下企业的行为 Le comportement de la firme en situation de concurrence

企业的目标：企业希望通过最大化利润 maximiser son profit 来进行生产。
利润最大化公式:

\[ \operatorname{Max} \pi(Q)=p Q-C T(Q) \]

其中， \(p\) 为市场价格， \(Q\) 为产量， \(C T(Q)\) 为总成本。
价格接受者: 企业在完全竞争市场中是价格接受者（price taker，preneuse de prix），不能通过自身的行为影响市场价格pas conscience de pouvoir influencer le prix 。
一阶条件 (condition de Premier Ordre):

\[ \frac{d \pi(Q)}{d Q}=p-\frac{d C T(Q)}{d Q}=0 \]

其中， \(\frac{d C T(Q)}{d Q}=C m(Q)\) ，即边际成本。

产量条件：企业会生产的产量满足以下条件：

\[ p=C m(Q) \]

完全竞争下的市场动态 Le comportement de la firme en situation de concurrence

当市场中有利润机会 opportunités de profits 时，新企业会进入市场 de nouvelles entreprises entrent sur ce secteur，导致：
- 所有企业的总供给 quantités offertes 增加。
- 价格下降，从而降低每个企业的利润。
长期均衡：
- 在完全竞争的长期均衡下，企业的利润为零，且价格 \(p=CM=Cm\)。

生产函数的收益 Les rendements de la fonction production

生产函数的收益类型:
恒定收益 rendement constant

\[ \lambda Q=F(\lambda K, \lambda L) \text { ，其中 } \lambda>1 \text { 。 } \]
- 无论投入的资本和劳动如何增加，收益总是与增加的成本和劳动呈线性增长。
递增收益 rendement croissant

\[ \lambda Q<F(\lambda K, \lambda L) \]
- 生产要素按相同比例增加，但产量的增加比例更大
递减收益 rendement décroissant

\[ \lambda Q>F(\lambda K, \lambda L) \]
- 生产要素按相同比例增加，但产量的增加比例更小
Cobb-Douglas 生产函数：Cobb-Douglas 生产函数是一种常用的生产函数，表示产出 (Q) 与资本 (K) 和劳动 (L) 之间的关系：

\[ Q=K^\alpha L^{1-\alpha} \]
- 其中\(\alpha\) 是资本的产出弹性，\(1-\alpha\) 是劳动的产出弹性。该函数假设资本和劳动按比例对产量产生影响，且通常用于解释恒定收益的情况。

消费者剩余 Le surplus du consommateur

定义：

消费者剩余是指消费者愿意支付的价格与实际支付的价格之间的差异，反映了消费者从交易中获得的额外满意度 mesurer la satisfaction 。它可以看作是消费者的"福利"或"超额收益"。
计算公式:

\[ S=\int_0^{Q^*}\left(p(Q)-p^*\right) d Q \]
- 解释:
  - \(p(Q)\) 是消费者愿意支付的价格，即需求曲线上的价格。
  - \(p^*\) 是市场均衡价格，消费者实际支付的价格。
  - \(Q^*\) 是均衡交易量。

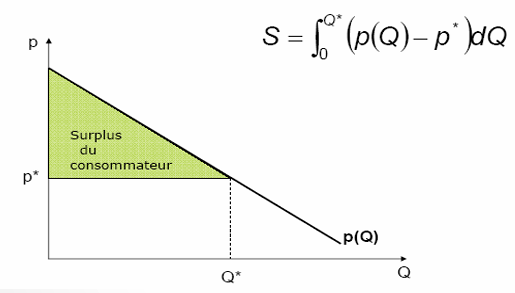
在需求曲线图中，消费者剩余是需求曲线和均衡价格线之间的面积，表示消费者的总超额效用。

完全竞争条件 Les conditions de la concurrence

完全竞争的假设条件：

完全竞争市场的假设条件非常严格，只有在以下条件下才能成立：
1. 原子性 Hypothèse d’atomicité：市场上有大量企业，每个企业的市场份额都很小，单个企业无法影响市场价格。
2. 产品同质性 Biens homogènes：市场上的所有产品完全相同，消费者不关心产品的来源。
3. 自由进入和退出 Libre-entrée：企业可以随时进入或退出市场，没有障碍。
4. 完全信息 Information parfaite：所有市场参与者都能完全获取市场价格和条件的信息。
5. 非排他性商品 Biens exclusifs：商品是公共的，不能排斥其他人使用。
完全竞争条件难以实现的原因：

在现实中，完全竞争的条件几乎从未完全实现，主要原因包括：
1. 原子性假设常常不满足：许多行业由少数企业主导，形成寡头或垄断市场。
2. 产品差异性：不同企业提供的产品存在质量或特性的差异。
3. 进入壁垒：技术要求、研发成本或法规限制使得新企业难以进入。
4. 信息不对称：企业和消费者之间信息不对称，尤其在保险等行业，信息差异影响市场效率。
5. 外部性：如污染等外部性问题，市场价格无法反映生产的全部社会成本。

市场失灵 défaillances de marchés

经济物品的特征 Les caractéristiques des biens économiques

竞争性 (Rivalité, rival)：当一个物品是竞争性时，意味着两个经济主体不能同时享用该物品。换句话说，一方使用了该物品，另一方就不能同时使用。
- 举例：一辆车是竞争性的，因为一个人使用了它，其他人就无法同时使用。
排他性 (Exclusivité, exclusif)：一个物品是排他性的，意味着只有支付了价格的消费者才能使用该物品。
- 举例：私人物品如汽车是排他性的，只有购买或租赁的人才能使用它。
私人消费品的双重特性：传统的私人消费品 Les biens et services de consommation privée traditionnelle 通常既是排他性的，也是竞争性的。只有那些支付了价格的人才能使用该物品，并且使用者间存在竞争。

物品的分类 Classification des biens

物品可以根据其竞争性和排他性进行分类：

竞争性与排他性物品：
- 举例：汽车
- 解释：使用汽车需要支付费用（排他性），而且使用时他人无法同时使用（竞争性）。
非竞争性与非排他性物品（公共物品 Biens communs）：
- 举例：电视节目或应用软件
- 解释：电视节目不论多少人观看，内容质量不受影响（非竞争性）；大多数人可以免费获取节目或应用（非排他性）。
公共物品 Biens communs 与公共资源 Biens publics 的区别：
- 公共物品：既非竞争性又非排他性，如国防或空气。
- 公共资源：具有竞争性但不排他性，如渔业资源，这就引发了“公地悲剧”问题。即过度使用公共资源导致其枯竭或破坏。

外部性 Externalités

定义：外部性是指一个经济主体的行为影响到了其他主体 autre agent 的利益，而这种影响没有通过市场进行补偿或支付n’est pas compensé dans le cadre d’un échange ou d’un marché。
- 例如，生产过程中的污染会影响周围居民的健康和环境，但生产企业无需为此支付补偿。
外部性分类：
1. 正外部性 (Externalité positive)：对其他经济主体产生了正面影响。
  - 举例：公共科研机构的研究可能对私营企业的研发产生积极影响，提升全社会的技术水平。
2. 负外部性 (Externalité négative)：对其他经济主体产生了负面影响。
  - 举例：
    - 工厂排放污染物导致周围居民健康受损。
    - 气候变化带来的全球环境问题，COVID-19 也被视为负外部性影响的例子。

外部性与最优资源配置 Externalités et allocation optimale

问题：当外部性存在时，市场配置资源往往不能达到社会的最优水平。
- 解释：市场上没有充分考虑到外部性带来的社会成本和社会效益，因此可能导致资源的误配。
- 正外部性：产生正外部性的活动通常供给不足。
- 负外部性：产生负外部性的活动通常供给过多。
经济解决方案：
1. 对负外部性活动征税 taxer：如对污染排放征收碳税，通过提高成本减少企业的污染行为。
2. 对正外部性活动进行补贴 subventionner：如资助科研活动或鼓励创新，通过降低成本促进这些有益社会的活动。

市场结构的实际类型 différentes structures de marché

市场可以根据供给者和需求者的数量 le nombre d’offreurs et de demandeurs 及产品差异化程度 la plus ou moins forte différenciation 进行分类，常见的市场结构包括：

垄断 (Monopole)：一个供给者控制整个市场，没有竞争对手，产品没有替代品。
寡头 (Oligopole)：少数几个企业主导市场，企业间可能存在激烈的价格竞争或合作。
完全竞争 (Concurrence parfaite)：大量供给者和需求者，产品完全同质，市场信息完全透明，企业和消费者都无法影响市场价格。

垄断 monopole

原子性假设的破除 Remise en cause de l’atomicité

在垄断的极端情况下，一个垄断者 monopole 面对众多的需求者。与完全竞争市场不同，垄断市场中只有一个卖家，因此原子性假设不再成立。
- 解释：原子性假设要求市场上有很多供应者，单个供应者无法影响市场价格，而在垄断市场中，只有一个企业控制市场，能够直接影响价格。
价格制定者 (Price Maker)：
- 在完全竞争市场中，企业是价格接受者 (price-taker)，它们无法影响市场价格，只能接受市场上既定的价格。
- 然而在垄断市场中，企业是价格制定者 (price-maker)，它决定的产量会影响市场价格。垄断企业可以根据需求函数 \(Q(p)\) 来调整价格和产量。

垄断企业的行为 Le comportement de la firme en monopole

利润最大化：垄断企业的目标是最大化利润，公式如下：\(Max π(Q)=p(Q)Q−CT(Q)\)
- 这里 \(p(Q)\) 是与产量 \(Q\) 对应的价格，因为垄断者通过控制产量影响市场价格。\(CT(Q)\) 是总成本。
一阶条件 (Condition du Premier Ordre)：

\[ \frac{d \pi(Q)}{d Q}=\underbrace{\frac{d p(Q)}{d Q} Q+p(Q)}_{\begin{array}{c}\text { Recette } \\\text { marginale }\end{array}}-\underbrace{\frac{d C T(Q)}{d Q}}_{\begin{array}{c}\text { Coût } \\\text { marginal }\end{array}}=0 \]
垄断企业会选择生产使得边际收益 (Rm, Recette marginale) 等于边际成本 (Cm, Coût marginal) 的产量。

边际收益的表达式 Expression de la recette marginale

边际收益公式：通过需求价格弹性公式，可以将边际收益 \(R m(Q)\) 重写为:

\[ R m(Q)=\frac{d p(Q)}{d Q} Q+p(Q)=\left(\frac{1}{\varepsilon}\right) p(Q)+p(Q) \]
\(\varepsilon\) 是需求价格弹性，表示价格变动对需求量的影响。当需求弹性较高时，价格对需求的影响较大。
利润最大化条件：垄断企业在利润最大化时，会选择一个产量，使得边际收益等于边际成本：

\[ p(Q)\left(1+\frac{1}{\varepsilon}\right)=C m(Q) \]

垄断价格 Le prix de monopole

垄断价格公式：通过边际收益等于边际成本的条件，可以得到垄断价格 \(p(Q)\) 的表达式：

\[ p(Q)=\frac{C m(Q)}{1+\frac{1}{\varepsilon}}，\varepsilon \in[-\infty,-1] \]
当需求价格弹性 \(\varepsilon\) 越小（即需求越不敏感于价格），垄断价格越高。相较于完全竞争市场中的价格 \(p^c\) ，垄断市场的价格 \(p^M\) 较高，产量较低。

\[ p^M=\frac{C m(Q)}{1+1 / \varepsilon}>C m(Q)=p^c \]
价格与弹性关系：
- 当需求弹性较小时（\(\varepsilon \rightarrow-1\)），垄断企业的定价能力更强，价格更高。
- 当需求弹性较大时，垄断价格趋近于边际成本 \(C m(Q)\)

利润率与边际成本 Marge et taux de marge

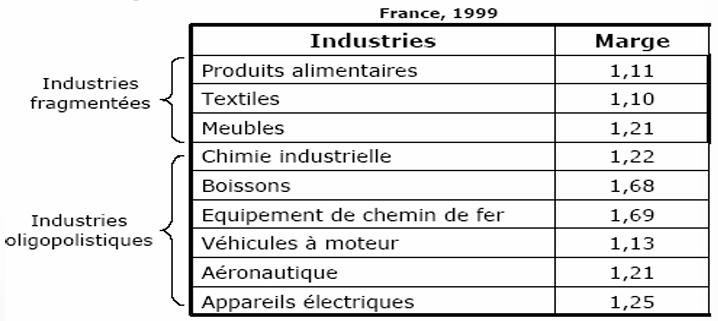
利润率 (Marge)：利润率是指价格与边际成本的比值

\[ \text { Marge }=\frac{p^M}{C m} \]
利润率差 (Taux de Marge)：利润率差是价格与边际成本之间的差距，以边际成本为基准

\[ \text { Taux de Marge }=\frac{p^M-C m}{C m} \]

利润率差反映了垄断企业如何通过控制价格来获得比边际成本更高的收益。

垄断的低效性

社会剩余损失 Le surplus social：垄断市场中，社会总福利（包括消费者剩余和生产者剩余）低于完全竞争市场。这个损失称为垄断的“无谓损失” (Charge morte)。
在完全竞争市场中，社会剩余为蓝色、黄色和绿色三部分之和。
而在垄断市场中，社会剩余仅为蓝色和黄色部分，绿色部分的无谓损失反映了社会福利的净减少。

实例 Les interactions stratégiques

现实中的市场结构 Les interactions stratégiques

在之前我们讨论了完全竞争和垄断两种极端的市场结构。然而，现实中更多的市场结构处于这两者之间，尤其是存在寡头市场的情况。寡头市场的特点是：

存在少数几家大企业，它们共同占据市场的大部分份额。
企业之间存在相互依存性 phénomène d’interdépendance，即一家企业的行为（如产量或价格）会影响其他企业的行为。
企业之间的战略互动 phénomène de stratégies 是市场的重要特征，企业需要考虑竞争对手的反应来制定自己的策略。

寡头理论 La théorie de l’oligopole 可以用来解释这些现象，特别是通过以下几种战略模型来描述企业之间的互动行为。

双头垄断模型 Duopole

双头垄断是寡头市场的一种极端情况，即市场上只有两家企业.

Cournot 模型

Cournot 模型由 Antoine Augustin Cournot 于 1838 年提出，是第一个用于描述企业行为的数学模型。它假设市场上只有两家企业，且每家企业根据对方的产量决定自己的产量

模型设定:
- 两家企业 1 和 2 生产同质产品，产量分别为 \(q_1\)和 \(q_2\) 。
- 成本函数： \(C_1=c_1 \cdot q_1\) 和 \(C_2=c_2 \cdot q_2\) 。
- 市场总供给： \(Q=q_1+q_2\) 。
- 需求函数：市场价格 \(p(Q)\) 由市场上的总供给决定，公式为:
  
  \[ p(Q)=A-\left(q_1+q_2\right) \]
  
  其中 \(A\) 是需求的截距，反映了最大愿意支付价格。
战略变量 variables stratégiques：在 Cournot 模型中，每家企业的战略变量是产量，即每家企业决定自己生产的数量 \(q_1\) 和 \(q_2\) ，并根据对方的产量选择最优的生产量。

Cournot 模型中的生产决策

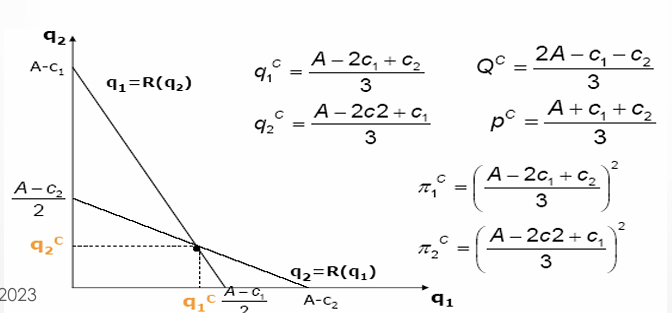
利润最大化: 每家企业的目标是最大化利润，假设企业 1 和 2 分别以 \(q_1\) 和 \(q_2\) 为已知条件，计算利润公式如下:

\[ \begin{aligned} & \pi_1\left(q_1, q_2\right)=p\left(q_1+q_2\right) q_1-C_1\left(q_1\right) \\ & \pi_2\left(q_1, q_2\right)=p\left(q_1+q_2\right) q_2-C_2\left(q_2\right) \end{aligned} \]

每个企业会选择一个使其利润最大化的产量，考虑到另一个企业的产量不变。

一阶条件 (CPO，Les conditions du premier ordre)：通过对利润函数对产量求导，并令其等于零，我们可以得到一阶条件:

\[ \frac{d \pi_1\left(q_1, q_2\right)}{d q_1}=0, \quad \frac{d \pi_2\left(q_1, q_2\right)}{d q_2}=0 \]

这两个方程可以用来求解每家企业的最优产量。

\[ \begin{aligned}& F R_1: q_1=R_1\left(q_2\right)=\frac{A-c_1-q_2}{2} \\& F R_2: q_2=R_2\left(q_1\right)=\frac{A-c_2-q_1}{2}\end{aligned} \]

Cournot 均衡是指每家企业都选择了最佳的产量水平，使得在给定对方产量的情况下，它们的决策是最优的。此时，任何一方改变其产量都不会增加自己的利润。

\[ \begin{gathered}q_1^c=\frac{A-2 c_1+c_2}{3}, \quad q_2^c=\frac{A-2 c_2+c_1}{3} \\Q^c=q_1^c+q_2^c=\frac{2 A-c_1-c_2}{3}, \quad p^c=\frac{A+c_1+c_2}{3}\end{gathered} \]
利润

\[ \pi_1^c=\left(\frac{A-2 c_1+c_2}{3}\right)^2, \quad \pi_2^c=\left(\frac{A-2 c_2+c_1}{3}\right)^2 \]

Cournot 均衡是寡头市场中一种典型的非合作博弈均衡，它反映了企业如何在相互依赖的情况下，通过产量决策实现利润最大化。

Bertrand 模型

与 Cournot 模型不同，Bertrand 模型假设企业之间的竞争是基于价格 prix 而非产量。即每个企业都试图通过调整价格来吸引更多的市场需求。

假设：

产品同质性：市场上的两家企业生产的是完全相同的产品，没有质量差异。
需求函数：市场需求函数为 \(D(p)\)，两家企业如果定价相同，则均分市场需求。否则，价格较低的企业会占据整个市场。
成本函数：假设两家企业的成本相同，且为常数 \(C_1=C_2=C\) 。企业的成本随产量线性变化，即 \(C_T\left(q_1\right)=c \cdot q_1\) 和 \(C_T\left(q_2\right)=c \cdot q_2\) 。

\[ \left\{\begin{array}{llll}D_1=D\left(p_1\right) \quad \text { et } \quad D_2=0 & \text { si } & p_1<p_2 \\D_1=D_2=\frac{D\left(p_1\right)}{2} & \text { si } & p_1=p_2 \\D_1=0 \quad \text { et } \quad D_2=D\left(p_2\right) & \text { si } & p_1>p_2\end{array}\right. \]

利润公式：

\[ \pi_1\left(q_1\right)=\left(p_1-c\right) \cdot q_1, \quad \pi_2\left(q_2\right)=\left(p_2-c\right) \cdot q_2 \]

每个企业都会尝试设定一个低于竞争对手的价格以赢得整个市场的需求，但这会导致价格逐渐逼近边际成本。

价格均衡：在 Bertrand 均衡下，企业的最优定价是将价格定为边际成本 c，即：

\[ p_1=p_2=c \]

两家企业在非合作情况下，通过价格竞争逐步压低价格，直到价格等于边际成本，此时两家企业的利润为零。这与完全竞争市场中的结果相同。
结论：Bertrand 均衡导致市场价格等于边际成本 \(p_1=p_2=c\)，两家企业无法从市场中获得超额利润。

Bertrand 模型的扩展：成本差异

不同成本情况下的 Bertrand 均衡：当两家企业的生产成本不同，即 \(c_1 \neq c_2\)，定价较低的企业会占据整个市场。成本更低的企业可以通过设置一个略高于 \(c_2\) 的价格来赢得市场：\(p_1 = c_2 - \epsilon\)

其中 \(\epsilon\) 是一个非常小的量，使得企业 2 无法继续盈利。

限制价格策略 (Prix-limite)：成本较低的企业可以通过定价低于对手的成本来迫使竞争对手退出市场，从而占据全部市场份额。

Stackelberg 双头垄断模型

在 Stackelberg 模型中，两家企业并不是对等的。一家企业处于领导者 (leader) 地位，另一家企业则是追随者 (follower)。这种不对称性使得 Stackelberg 模型与 Cournot 模型的同时决策不同。领导者首先选择产量，追随者根据领导者的选择再做出反应。这是一个序列博弈 (jeu séquentiel)，其中领导者首先行动，追随者随后根据领导者的行为选择最佳反应。解决这种博弈的方法是逆向归纳法 (backward induction)，即从后续步骤推导出前期的最优决策。

追随者的反应

追随者决策：企业 2 作为追随者，观察到领导者（企业 1 ）的产量 \(q_1\) 后，选择使利润最大化的产量 \(q_2\) 。追随者的利润最大化问题为:

\[ \operatorname{Max}_{q_2} \pi_2\left(q_1, q_2\right)=p\left(q_1, q_2\right) q_2-C_2\left(q_2\right) \]

其中，价格函数为 \(p\left(q_1, q_2\right)=A-\left(q_1+q_2\right)\) ，而 \(C_2\left(q_2\right)=c_2 \cdot q_2\) 为企业 2 的总成本。
一阶条件：追随者通过对利润函数对 \(q_2\) 求导并令其等于零，可以得到反应函数：

\[ \frac{d \pi_2\left(q_1, q_2\right)}{d q_2}=0 \]
反应函数：企业 2 的反应函数 \(R_2\left(q_1\right)\) 是对企业 1 的产量 \(q_1\) 做出的最优反应，与 Cournot 模型中的反应函数相同:

\[ R_2\left(q_1\right)=\frac{A-c_2-q_1}{2} \]

领导者的决策

领导者决策：企业 1 作为领导者，知道企业 2 的反应函数 \(R_2\left(q_1\right)\) ，并基于此选择最优的产量 \(q_1\) 。领导者的利润最大化问题为:

\[ \operatorname{Max}_{q_1} \pi_1\left(q_1, q_2\right)=p\left(q_1, q_2\right) q_1-C_1\left(q_1\right) \]

其中 \(q_2=R_2\left(q_1\right)=\frac{A-c_2-q_1}{2}\) ，领导者根据追随者的反应函数来决定产量。
一阶条件：对领导者的利润函数求导并令其等于零，得到:

\[ \frac{d \pi_1\left(q_1, q_2\right)}{d q_1}=0 \]
领导者的最优产量：求解得到领导者的最优产量为：

\[ q_1^{S L}=\frac{A-2 c_1+c_2}{2} \]

领导者的产量 \(q_1^{S L}\) 比 Cournot 模型中的产量 \(q_1^c\) 更高。

Stackelberg 均衡

追随者的产量: 通过代入领导者的最优产量 \(q_1^{S L}\) 到追随者的反应函数中，可以求得追随者的最优产量:

\[ q_2^{S F}=\frac{A-2 c_2+c_1}{4} \]

追随者的产量低于 Cournot 均衡中的产量 \(q_2^c\) 。
均衡价格：市场均衡价格为:

\[ p^{S L}=\frac{A+2 c_1+c_2}{4} \]
利润: 领导者和追随者的利润分别为:

\[ \pi_1^{S L}=\frac{\left(A-2 c_1+c_2\right)^2}{8}, \quad \pi_2^{S F}=\frac{\left(A-3 c_2+2 c_1\right.}{4} \]

领导者的利润 \(\pi_1^{S L}\) 大于在 Cournot 模型中的利润，而追随者的利润则低于 Cournot 模型中的利润。

合谋/卡特尔协议 Entente Collusive ou Cartel

合谋

合作策略 stratégies coopératives：在寡头市场中，企业可以通过合作策略形成合谋（卡特尔），共同决定产量和价格，以最大化总利润。
行为方式：企业组成卡特尔后，行为类似于一个拥有多个分支的垄断者，尽管每个企业的成本可能不同，但它们共同决定市场的供给。

稳定性

不稳定性：虽然卡特尔可以通过减少产量、抬高价格来提高利润，但这种协议通常不稳定。因为每个企业都有动机通过“作弊 ne pas respecter l’accord ”增加产量，从而获取更多利润。
诱因：每家企业都有动力去生产比协议中规定的更多的产量，原因是增加的产量可以使其获得比卡特尔协议中的利润更多的收益，这导致卡特尔协议很难维持长期的稳定性。

利润最大化

总利润最大化: 卡特尔的目标是选择 \(q_1\) 和 \(q_2\) (两家企业的产量），以最大化总利润。利润最大化的公式如下:

\[ \operatorname{Max}_{q_1, q_2} \pi=\pi_1+\pi_2=p\left(q_1, q_2\right)\left(q_1+q_2\right)-C_1\left(q_1\right)-C_2\left(q_2\right) \]

一阶条件 (C.P.O): 通过对利润函数分别对 \(q_1\) 和 \(q_2\) 求导

\[ \begin{aligned}& \frac{d \pi}{d q_1}=p\left(q_1, q_2\right)+\frac{d p\left(q_1, q_2\right)}{d q_1}\left(q_1+q_2\right)-\frac{d C_1\left(q_1\right)}{d q_1}=0 \\& \frac{d \pi}{d q_2}=p\left(q_1, q_2\right)+\frac{d p\left(q_1, q_2\right)}{d q_2}\left(q_1+q_2\right)-\frac{d C_2\left(q_2\right)}{d q_2}=0\end{aligned} \]

成本相同情况下的卡特尔均衡

相同成本假设: 如果两家企业的成本相同（即 \(c_1=\left.c_2=c\right)\) ，并且市场的需求函数为 \(p=A-\left(q_1+q_2\right)\) ，我们可以得到以下均衡解：

\[ \begin{gathered} q_1^{\text {cartel }}=q_2^{\text {cartel }}=\frac{A-c}{4} \\ p^{\text {cartel }}=\frac{A+c}{2} \\ Q^{\text {cartel }}=q_1^{\text {cartel }}+q_2^{\text {cartel }}=\frac{A-c}{2} \\ \pi_1^{\text {cartel }}=\pi_2^{\text {cartel }}=\left(\frac{A-c}{2}\right)^2 \end{gathered} \]

作弊情景

单个企业作弊 triche：如果企业1作弊，生产多于协议规定的 22.5 个单位，例如生产 27.5 个单位:

\[ \begin{gathered} q_1^{\text {triche }}=27.5, \quad p^{\text {triche }}=50, \quad Q^{\text {triche }}=50 \\ \pi_1^{\text {triche }}=1100, \quad \pi_2^{\text {cartel }}=900 \end{gathered} \]

这样，企业 1 获得了更高的利润，而企业 2 的利润则减少。

两家企业同时作弊：如果两家企业都选择增加产量到 27.5 个单位，市场均衡会进一步改变：

\[ \begin{gathered} q_1^{\text {triche }}=q_2^{\text {triche }}=27.5, \quad p^{\text {triche }}=45 \\ \pi_1^{\text {triche }}=\pi_2^{\text {triche }}=962.5 \end{gathered} \]

在这种情况下，两家企业都比合作时获得更少的利润。