C2 状态空间表示、可控性与可观性 Représentation d'état, commandabilité, observabilité
C2 PLAN
1. 状态空间表示回顾
- 一般情况、线性不变系统(SLI)连续时间
- 状态方程的解法
- 采样系统
- 稳定性
- 状态 ↔︎ 传递函数之间的转换
2. 基底变换
3. 可控性
- 定义及线性不变系统的必要和充分条件(CNS)
- 不可控系统的分解
4. 可观性
- 定义及线性不变系统的必要和充分条件(CNS)
- 不可观系统的分解
C2.1 状态的表示 Représentation d'état
🪺 状态模型
modèle d'état不仅捕捉了系统的输入-输出行为comportement entrée-sortie,还能够描述系统的内部行为le comportement interne du système。
因此,与只描述输入-输出行为的传递函数不同,状态空间表示法可以处理更广泛的系统类型,包括非线性和/或时变系统。
C2.1.1 定义 Définition
一个时间连续系统système à temps continu的状态空间表示Une représentation d'état
由两个方程来描述:
\[ \begin{aligned}& \dot{x}(t)=f(t, x(t), u(t)) \\& y(t)=h(t, x(t), u(t))\end{aligned} \]
其中:
- \(u(t) \in \mathbb{R}^m\) 是输入向量,
- \(x(t) \in \mathbb{R}^n\) 是状态向量,
- \(y(t) \in \mathbb{R}^p\) 是输出向量。
第一个方程描述状态\(x(t)\)向量随时间的演化,在\(t = t_0\)时,有\(x(t_0) =
x_0\)。这个方程被称为状态方程équation d’état 。
🪺 状态变量
variables d'état通常可以与物理量关联,例如位置、速度、角位移、转速、电流强度、电压、温度、压力等,尽管这不是强制性的。任何状态变量的线性组合也可以视为状态变量。
第二个方程描述输出\(y(t)\)与状态变量和输入的关系。被称为输出方程或者观测方程équation de sortie ou d'observation。
CE2.1 例- 小车上的倒立摆
考虑如下示例:
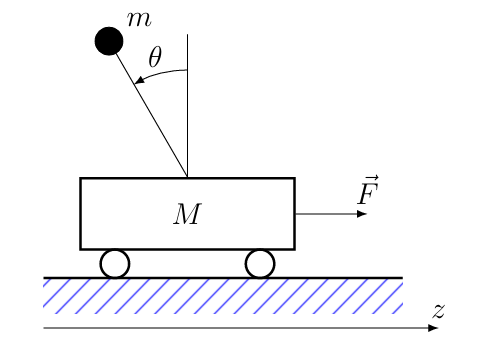
忽略对力学问题的探讨,已知通过拉格朗日方法可以直接得到运动方程:·
\[ \begin{aligned}(m+M) \ddot{z}-m l \ddot{\theta} \cos \theta+m l \dot{\theta}^2 \sin \theta & =F \\l \ddot{\theta}-\ddot{z} \cos \theta-g \sin \theta & =0\end{aligned} \]
在本实例下分析和探讨状态方程。
本系统的状态向量:·\(x=\left(x_1, x_2, x_3, x_4\right)^{\top}=(z, \theta, \dot{z}, \dot{\theta})^{\top}\)。特别需要注意的是,状态方程中只出现一阶导。输入\(u = F\),输出\(y = z\)。
观察两个方程,每个方程中都同时涉及\(\ddot \theta\)和\(\ddot z\),将其写作矩阵形式得到:
\[ \underbrace{\left(\begin{array}{cc}m+M & -m l \cos \theta \\-\cos \theta & l\end{array}\right)}_{=\mathcal{M}(\theta)}\binom{\ddot{z}}{\ddot{\theta}}=\underbrace{\binom{F-m l \dot{\theta}^2 \sin \theta}{g \sin \theta}}_{=G(\theta, F)} \]
在物理中,前者被称为质量矩阵,后者被称为广义力。
质量方程的行列式\(\operatorname{det} \mathcal{M}(\theta)=l\left(M+m \sin ^2 \theta\right)>0\),质量矩阵有逆,方程可解。
\[ \binom{\ddot{z}}{\ddot{\theta}}=\mathcal{M}(\theta)^{-1} G(\theta, F)=\frac{1}{l\left(M+m \sin ^2 \theta\right)}\binom{l F-m l^2 \dot{\theta}^2 \sin \theta+m g l \sin \theta \cos \theta}{F \cos \theta-m l \dot{\theta}^2 \sin \theta \cos \theta+(m+M) g \sin \theta} \]
由此可以推导出状态方程:
\[ f(t, x, u)=f(x, u)=\left(\begin{array}{c}x_3 \\x_4 \\\frac{u-m l x_4^2 \sin x_2+m g \sin x_2 \cos x_2}{M+m \sin ^2 x_2} \\\frac{u \cos x_2-m l x_4^2 \sin x_2 \cos x_2+(m+M) g \sin x_2}{l\left(M+m \sin ^2 x_2\right)}\end{array}\right) \]
而输出方程很简单:
\[ h(t, x, u)=h(x)=x_1 \]
回到状态空间的表示。
当输入为标量时,称其为单输入系统
système mono-entrée。
当输出为标量时,称其为单输出系统système mono-sortie
。
当输入输出均为标量时,称之为单变量系统/单输入单输出系统(SISO,Single Input Single Output)
,CE2.1探讨的就是这种情况。
在相反的情况下,称之为多输入多输出系统(MIMO,Multi Input Multi Output)
。
在研究状态空间时,首先要确定方程是否是柯西问题cauchy problem
,即常微分方程界的存在性和唯一性。为此,比较常用的方法是柯西-利普希茨定理le théorème de Cauchy Lipchitz
,为此,需要保证向量场连续,且在\(x\)上满足局部利普希茨条件。
🪺 柯西-利普希茨定理(
Cauchy-Lipschitz Theorem),又称皮卡-林德勒夫定理(Picard-Lindelöf Theorem),是常微分方程中的一个重要定理,保证了某些微分方程的局部解的存在性和唯一性。 具体而言,该定理讨论的是以下形式的初值问题: \(\frac{d y}{d x}=f(x, y), \quad y\left(x_0\right)=y_0\) 假设函数 \(f(x, y)\) 对于 \(x\) 和 \(y\) 是连续的,并且在 \(y\) 上满足利普希茨条件,即存在常数 \(L\) ,使得对于所有 \(x\) 和任意的 \(y_1, y_2\) ,有: \(\left|f\left(x, y_1\right)-f\left(x, y_2\right)\right| \leq L\left|y_1-y_2\right|\) 那么,在初值 \(\left(x_0, y_0\right)\) 附近的某个区间上,初值问题存在唯一解。
状态空间并非唯一的,如:
\[ \begin{aligned}& \dot{z}(t)=T^{-1} f(t, T z(t), u(t)) \\& y(t)=h(t, T z(t), u(t))\end{aligned} \]
与原始的状态空间表示完全一致。
C2.1.2 不同的系统
时不变系统 Système invariant
时不变invariant
是描述系统的状态与初始时刻无关的性质,即\(x(t)
= x(t+t_0)\)。
更加具体的说:
🪺 状态空间表示被称为时不变系统,当且仅当对于任意初始时刻 \(t_0 \in \mathbb{R}\) 任意初始条件 \(x_0 \in \mathbb{R}^n\) 、任意控制输入 \(v:\left[t_0,+\infty\right) \rightarrow \mathbb{R}^m\) 和任意 \(h>0\) ,设 \((x(t), y(t))\) 是系统在初始条件 \(x\left(t_0\right)=x_0\) 和输入 \(u(t)=v(t)\) 下的解,则 \((\tilde{x}(t), \tilde{y}(t))=(x(t-h), y(t-h))\) 是同一系统在初始条件 \(\tilde{x}\left(t_0+h\right)=x_0\) 和输入 \(u(t)=v(t-h)\) 下的解。
简单来说,时不变系统的状态形式为:
\[ \begin{aligned}& \dot{x}(t)=f(x(t), u(t)) \\& y(t)=h(x(t), u(t))\end{aligned} \]
即\(f: \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}^n\) 和 \(h: \mathbb{R}^n \times \mathbb{R}^m \rightarrow \mathbb{R}^p\)与时间无关。
在实际情况下,当方程中涉及的系数都与时间无关时,系统为时不变的。如CE2.1中,如果\(m,M,l,g\)都与时间无关,则系统是时不变的。
线性系统 Système linéaire
线性系统是控制论的核心。当向量场\(f\)和\(h\)对\(x\)和\(u\)都为线性时,系统称为线性系统,表示为:
\[ \begin{aligned}\dot{x}(t) & =A(t) x(t)+B(t) u(t) \\y(t) & =C(t) x(t)+D(t) u(t)\end{aligned} \]
其中:
- \(A(t) \in \mathbb{R}^{n \times n}\) 是演化矩阵,
- \(B(t) \in \mathbb{R}^{n \times m}\) 是控制矩阵,
- \(C(t) \in \mathbb{R}^{p \times n}\) 是输出矩阵,
- \(D(t) \in \mathbb{R}^{p \times m}\) 是直接传输矩阵。
线性时不变系统 Système linéaire et invariant
结合线性和时不变两个性质,线性时不变系统表示为:
\[ \begin{aligned}\dot{x}(t) & =A x(t)+B u(t) \\y(t) & =C x(t)+D u(t)\end{aligned} \]
这种形式的方程有显式解:
\[ \begin{aligned} & x(t)=e^{A\left(t-t_0\right)} x\left(t_0\right)+\int_{t_0}^t e^{A(t-\tau)} B u(\tau) d \tau \\ & y(t)=C e^{A\left(t-t_0\right)} x\left(t_0\right)+\int_{t_0}^t C e^{A(t-\tau)} B u(\tau) d \tau+D u(t) \end{aligned} \]
状态解的第一部分称为自由响应régime libre ,
表示在没有输入\(u=0\)
的情况下,系统响应初始条件 \(x\left(t_0\right)\)
的状态变化。第二部分称为受迫相应régime forcé
,表示系统对外部刺激的相应。
\[ \Phi\left(t, t_0\right)=e^{A\left(t-t_0\right)} \triangleq \sum_{k \geq 0} \frac{\left(t-t_0\right)^k A^k}{k!} \]
解中,\(e^{A\left(t-t_0\right)}\)被称为状态转移矩阵,是通过矩阵指数计算的。可以如下计算:
\[ e^{A t}=I+A t+A^2 \frac{t^2}{2!}+A^3 \frac{t^3}{3!}+\ldots \]
或者使用拉普拉斯变换来表示:
\[ e^{A t}=\mathcal{L}^{-1}\left((s I-A)^{-1}\right) \]
关于矩阵指数的显式计算方法,可以使用Sylvester插值法或者Jordan标准形。
Sylvester 插值法
Jordan标准化方法
C2.1.3 在平衡点附近线性化 Linéarisation autour d'un point d'équilibre
为了方便计算,需对更为常见的非线性系统在平衡点附近进行线性化。
本章考虑非线性时不变系统:
\[ \begin{aligned}\dot{x}(t) & =f(x(t), u(t)) \\y(t) & =h(x(t), u(t))\end{aligned} \]
平衡点
Point d’équilibre ou équilibre
平衡点\((\bar{x}, \bar{u}) \in \mathbb{R}^n \times \mathbb{R}^m\)满足\(f(\bar{x}, \bar{u})=0\)。即平衡点系统状态在时间上保持不变。其解满足:
\[ \bar{y}=h(\bar{x}, \bar{u}) \]
在自治系统 système autonome 中,平衡点满足\(f(\bar{x})=0\)。
平衡点并非一定存在。
另一种表示形式使用如下记号表示平衡点:
\[ f\left(x^{\star}, u^{\star}\right)=0 \]
CE2.2 例- 小车上的倒立摆中的平衡点
考虑已经得到的状态方程,平衡点要求:
\[ \begin{aligned} \bar{x}_3 & =0 \\ \bar{x}_4 & =0 \\ \frac{\bar{u}-m l \bar{x}_4^2 \sin \bar{x}_2+m g \sin \bar{x}_2 \cos \bar{x}_2}{M+m \sin ^2 \bar{x}_2} & =0 \\ \frac{\bar{u} \cos \bar{x}_2-m l \bar{x}_4^2 \sin \bar{x}_2 \cos \bar{x}_2+(m+M) g \sin \bar{x}_2}{l\left(M+m \sin ^2 \bar{x}_2\right)} & =0 \end{aligned} \]
经过简化,得到:
\[ \begin{aligned}\bar{x}_3=\bar{x}_4 & =0 \\\bar{u}+m g \sin \bar{x}_2 \cos \bar{x}_2 & =0 \\\bar{u} \cos \bar{x}_2+(m+M) g \sin \bar{x}_2 & =0\end{aligned} \]
联立后两个方程:
\[ \sin \bar{x}_2 \underbrace{\left(M+m \sin ^2 \bar{x}_2\right)}_{>0}=0 \]
这意味着 \(\sin \bar{x}_2=0\) ,即 \(\bar{x}_2=0\) 或 \(\bar{x}_2=\pi\) 。这两个解对应倒立摆的两个平衡状态:
- 当 \(\bar{x}_2=0\) 时,摆处于向下稳定状态。
- 当 \(\bar{x}_2=\pi\) 时,摆处于向上不稳定状态。
同时可以观察到\(\bar{u}=0\),\(\bar{x}_1 \in \mathbb{R}\)。也就是说,在外力为零的时候,存在两个平衡点。
然后我们尝试在平衡点附近对非线性状态模型进行近似。
偏导数 Dérivées partielles
当函数 \(x_l \mapsto\) \(f_k\left(a_1, \ldots, a_{l-1}, x_l, a_{l+1}, \ldots a_n\right)\) 在 \(x_l=a_l\) 处可导时,我们说 \(f_k\) 在点 \(a=\left(a_1, \ldots, a_n\right)^{\top} \in \mathbb{R}^n\) 相对于 \(x_l\) 存在偏导数。此时,该偏导数记为 \(\frac{\partial f_k}{\partial x_l}(a)\) 。如果每个 \(f_k\)在 \(a\) 处对所有 \(x_k\) 都有偏导数,则定义雅可比矩阵为:
\[ \frac{\partial f}{\partial x}=\left(\frac{\partial f_k}{\partial x_l}(a)\right)_{1 \leq k \leq m, 1 \leq l \leq n} \in \mathbb{R}^{m \times n} \]
在当前问题中,更为细致的:

如果\(f\)在每一个点对每一个\(x_k\)都有偏导数,且偏导数是连续的,那么我们称\(f\)是连续可微continumentdi érentiable的。
在这种条件下,可以在稳定点附近进行一阶泰勒展开。
\[ \begin{aligned}& \dot{x}(t)=\underbrace{f(\bar{x}, \bar{u})}_{=0}+\frac{\partial f}{\partial x}(\bar{x}, \bar{u})[x(t)-\bar{x}]+\frac{\partial f}{\partial u}(\bar{x}, \bar{u})[u(t)-\bar{u}]+O(\|(x(t), u(t))-(\bar{x}, \bar{u})\|) \\& y(t)=\underbrace{h(\bar{x}, \bar{u})}_{=\bar{y}}+\frac{\partial h}{\partial x}(\bar{x}, \bar{u})[x(t)-\bar{x}]+\frac{\partial h}{\partial u}(\bar{x}, \bar{u})[u(t)-\bar{u}]+O(\|(x(t), u(t))-(\bar{x}, \bar{u})\|)\end{aligned} \]
忽略高阶小量,并引入偏差量\(\delta x(t)=x(t)-\bar{x}, \delta u(t)=u(t)-\bar{u}, \delta y(t)=y(t)-\bar{y}\),即可得到线性化之后的线性时不变系统:
\[ \begin{aligned}\delta \dot{x}(t) & =A \delta x(t)+B \delta u(t) \\\delta y(t) & =C \delta x(t)+D \delta u(t)\end{aligned} \]
- \(A=\frac{\partial f}{\partial x}(\bar{x}, \bar{u})\)
- \(B=\frac{\partial f}{\partial u}(\bar{x}, \bar{u})\)
- \(C=\frac{\partial h}{\partial x}(\bar{x}, \bar{u})\)
- \(D=\frac{\partial h}{\partial u}(\bar{x}, \bar{u})\)
注意,首先,线性化必须在平衡点进行,雅可比矩阵必须是平衡点处的雅可比矩阵,简化仅在平衡点附近较好的模拟原有系统。
CE2.3 例- 小车上的倒立摆中的线性化
我们继续分析示例 3 中的倒立摆系统,已经知道系统的平衡点由以下条件定义:
\[ \bar{x}=\left(\bar{x}_1, \bar{x}_2, 0,0\right)^{\top} \in \mathbb{R}^4, \quad \bar{x}_1 \in \mathbb{R} \text { 任意 }, \quad \bar{x}_2 \in \pi \mathbb{Z}, \quad \bar{u}=0, \quad \bar{y}=\bar{x}_1 \]
现在,在这个平衡点处对系统的动力学进行线性化,得到的系统矩阵如下:
\[ A=\left(\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{m g}{M} & 0 & 0 \\ 0 & \frac{(m+M) g \cos \bar{x}_2}{M l} & 0 & 0 \end{array}\right), \quad B=\left(\begin{array}{c} 0 \\ 0 \\ \frac{1}{M} \\ \frac{\cos \bar{x}_2}{M l} \end{array}\right), \quad C=\left(\begin{array}{llll} 1 & 0 & 0 & 0 \end{array}\right), \quad D=0 \]
其中,关于 \(\cos \bar{x}_2\) 的值有以下情况:
- 如果 \(\bar{x}_2 \in 2 \pi \mathbb{Z}\) (即摆处于向下稳定位置),则 \(\cos \bar{x}_2=1\) ;
- 如果 \(\bar{x}_2 \in \pi+2 \pi \mathbb{Z}\) (即摆处于向上不稳定位置),则 \(\cos \bar{x}_2=-1\) 。
这些矩阵表示的是系统在平衡点处的线性近似。通过这个线性化模型,我们可以进一步分析系统的稳定性,并设计控制器来稳定系统。例如,当 \(\bar{x}_2=0\) 时,系统处于向下稳定状态;而当 \(\bar{x}_2=\pi\) 时,系统处于向上不稳定状态。
C2.1.4 从状态空间模型到传递函数 Passageétat-transfert
我们知道,线性时不变系统可以用传递函数或者传递矩阵来建模。这种建模被称为外部表示
représentation externe
,相应的,使用状态的表示方法被称为内部表示représentation interne。传递矩阵matricede transfert或传递函数(仅在单变量系统)描述输入与输出大的关系:
\[ Y(s)=H(s) U(s) \]
接下来我们讨论从内部表示转化到外部表示。
\[ \begin{aligned}\dot{x}(t) & =A x(t)+B u(t) \\y(t) & =C x(t)+D u(t)\end{aligned} \]
首先进行拉普拉斯变换,得到:
\[ \begin{aligned}s X(s) & =A X(s)+B U(s) \\Y(s) & =C X(s)+D U(s)\end{aligned} \]
注意我们假设了初始条件\(x(0) = 0\)。然后就可以直接得出传递函数的表达式:
\[ H(s)=C(s I-A)^{-1} B+D \]
- 传递函数的分母:在单输入单输出系统(SISO)的情况下,传递函数 \(H(s)\) 的分母是矩阵 \(A\) 的特征多项式(回忆上一章提到过的伴随矩阵法求逆),即 \(\operatorname{det}(s I-A)\) 。换句话说,传递函数的极点是矩阵 \(A\) 的特征值。(注意,反之并不一定)。
- 传递函数的阶数:传递函数的阶数(即分母多项式的最高次数)小于或等于状态空间表示的维度 \(n\) 。这意味着状态空间模型的维度限制了系统的动态复杂性。
CE2.4 例- 小车上的倒立摆的传递矩阵
考虑状态方程的标量形式:
\[ \begin{aligned}\delta \dot{x}_1 & =\delta x_3 \\\delta \dot{x}_2 & =\delta x_4 \\\delta \dot{x}_3 & =\frac{m g}{M} \delta x_2+\frac{1}{M} \delta u \\\delta \dot{x}_4 & =\frac{(m+M) g \cos \bar{x}_2}{M l} \delta x_2+\frac{\cos \bar{x}_2}{M l} \delta u \\\delta y & =\delta x_1\end{aligned} \]
进行拉普拉斯变换得到:
\[ \begin{aligned} s \Delta X_1(s) & =\Delta X_3(s) \\ s \Delta X_2(s) & =\Delta X_4(s) \\ s \Delta X_3(s) & =\frac{m g}{M} \Delta X_2(s)+\frac{1}{M} \Delta U(s) \\ s \Delta X_4(s) & =\frac{(m+M) g \cos \bar{x}_2}{M l} \Delta X_2(s)+\frac{\cos \bar{x}_2}{M l} \Delta U(s) \\ \Delta Y(s) & =\Delta X_1(s) \end{aligned} \]
简化方程可得:
\[ \begin{aligned}&\left(s^2-\frac{(m+M) g \cos \bar{x}_2}{M l}\right) \Delta X_2(s)=\frac{\cos \bar{x}_2}{M l} \Delta U(s)\\&s^2 \Delta X_1(s)=\frac{m g}{M} \Delta X_2(s)+\frac{1}{M} \Delta U(s)\end{aligned} \]
联立可得:
\[ \begin{aligned} s^2\left(s^2-\frac{(m+M) g \cos \bar{x}_2}{M l}\right) \Delta X_1(s) & =\frac{m g}{M} \cdot \frac{\cos \bar{x}_2}{M l} \Delta U(s)+\frac{1}{M}\left(s^2-\frac{(m+M) g \cos \bar{x}_2}{M l}\right) \Delta U(s) \\ & =\left(\frac{1}{M} s^2-\frac{g \cos \bar{x}_2}{M l}\right) \Delta U(s) \end{aligned} \]
从而得到传递函数:
\[ H(s)=\frac{\Delta X_1(s)}{\Delta U(s)}=\frac{\frac{1}{M} s^2-\frac{g \cos \bar{x}_2}{M l}}{s^2\left(s^2-\frac{(m+M) g \cos \bar{x}_2}{M l}\right)} \]
CE2.1.5 单变量情况下的从状态空间模型到传递函数 Passageétat-transfert cas monovariable
仅考虑在单变量情况下,从传递函数向状态空间的转变。在这种情况下,传递函数可以写作:
\[ H(s)=\frac{b_0+b_1 s+\ldots+b_{n-1} s^{n-1}}{a_0+a_1 s+\ldots+a_{n-1} s^{n-1}+s^n}+d_0 \]
并且满足传递函数是严格真分式,其分子的阶数小于或等于分母的阶数。
控制伴随形式
Forme compagnon pour la commande
传递函数形式为:
\[ Y(s)=Y_1(s)+d_0 U(s), \quad Y_1(s)=\frac{b_0+b_1 s+\cdots+b_{n-1} s^{n-1}}{a_0+a_1 s+\cdots+s^n} U(s) \]
引入\(W(s)=\frac{1}{a_0+a_1 s+\cdots+s^n} U(s)\),有
\[ Y_1(s)=\left(b_0+b_1 s+\cdots+b_{n-1} s^{n-1}\right) W(s) \]
在时间域上则有:
\[ \left\{\begin{aligned}y(t) & =y_1(t)+d_0 u(t) \\y_1(t) & =b_0 w(t)+b_1 \dot{w}(t)+\cdots+b_{n-1} w^{(n-1)}(t) \\w^{(n)}(t) & =-a_0 w(t)-a_1 \dot{w}(t)-\cdots-a_{n-1} w^{(n-1)}(t)+u(t)\end{aligned}\right. \]
然后如此选择状态变量:
\[ \begin{aligned} x_1(t) & =w(t) \\ x_2(t) & =\dot{x}_1(t)=\dot{w}(t) \\ x_3(t) & =\dot{x}_2(t)=\ddot{w}(t) \\ & \vdots \\ x_n(t) & =\dot{x}_{n-1}(t)=w^{(n-1)}(t) \end{aligned} \]
即可将状态方程表示为:
\[ \frac{\mathrm{d}}{\mathrm{d} t}\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_{n-1} \\ x_n \end{array}\right)(t)=\underbrace{\left(\begin{array}{ccccc} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ -a_0 & -a_1 & -a_2 & \cdots & -a_{n-1} \end{array}\right)}_{=A}\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_{n-1} \\ x_n \end{array}\right)(t)+\underbrace{\left(\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ 1 \end{array}\right)}_{=B} u(t) \]
并把输出方程表示为:
\[ y(t)=y_1(t)+d_0 u(t)=\underbrace{\left(\begin{array}{llll} b_0 & b_1 & \cdots & b_{n-1} \end{array}\right)}_{=C}\left(\begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_n \end{array}\right)(t)+\underbrace{d_0}_{=D} u(t) \]
观察伴随形式
Forme compagnon pour l'observation
不引入\(W(s)=\frac{1}{a_0+a_1 s+\cdots+s^n} U(s)\),而是将方程写成:
\[ Y_1(s)=\left(b_{n-1} \frac{1}{s}+\cdots+b_1 \frac{1}{s^{n-1}}+b_0 \frac{1}{s^n}\right) U(s)-\left(a_{n-1} \frac{1}{s}+\cdots+a_1 \frac{1}{s^{n-1}}+a_0 \frac{1}{s^n}\right) Y_1(s) \]
进而引入\(\zeta_j=b_j U(s)-a_j Y_1(s)\):
\[ Y_1(s)=\left(b_{n-1} \frac{1}{s}+\cdots+b_1 \frac{1}{s^{n-1}}+b_0 \frac{1}{s^n}\right) U(s)-\left(a_{n-1} \frac{1}{s}+\cdots+a_1 \frac{1}{s^{n-1}}+a_0 \frac{1}{s^n}\right) Y_1(s) \]
如下选择状态变量:
\[ \left\{\begin{aligned}X_n(s) & =\frac{1}{s}\left(b_{n-1} U(s)-a_{n-1} X_n(s)+X_{n-1}(s)\right) \\X_{n-1}(s) & =\frac{1}{s}\left(b_{n-2} U(s)-a_{n-2} X_n(s)+X_{n-2}(s)\right) \\& \vdots \\X_1(s) & =\frac{1}{s}\left(b_0 U(s)-a_0 X_n(s)\right)\end{aligned}\right. \]
在时间域上:
\[ \left\{\begin{array}{l}\dot{x}_1(t)=b_0 u(t)-a_0 x_n(t) \\\dot{x}_2(t)=b_1 u(t)-a_1 x_n(t)+x_1(t) \\\dot{x}_3(t)=b_2 u(t)-a_2 x_n(t)+x_2(t) \\\quad \vdots \\\dot{x}_n(t)=b_{n-1} u(t)-a_{n-1} x_n(t)+x_{n-1}(t)\end{array}\right. \]
由此可以写出状态空间表示:
\[ \begin{gathered}\frac{\mathrm{d}}{\mathrm{d} t}\left(\begin{array}{c}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n\end{array}\right)(t)=\underbrace{\left(\begin{array}{ccccc}0 & 0 & \cdots & 0 & -a_0 \\1 & 0 & \cdots & 0 & -a_1 \\\vdots & \vdots & \ddots & \vdots & \vdots \\0 & 0 & \cdots & 0 & -a_{n-2} \\0 & 0 & \cdots & 1 & -a_{n-1}\end{array}\right)}_{=A}\left(\begin{array}{c}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n\end{array}\right)(t)+\underbrace{\left(\begin{array}{c}b_0 \\b_1 \\\vdots \\b_{n-2} \\b_{n-1}\end{array}\right)}_{=B} u(t) \\y(t)=y_1(t)+d_0 u(t)=\underbrace{\left(\begin{array}{lllll}0 & 0 & \cdots & 0 & 1\end{array}\right)}_{=C}\left(\begin{array}{c}x_1 \\x_2 \\\vdots \\x_{n-1} \\x_n\end{array}\right)(t)+\underbrace{d_0}_{=D} u(t)\end{gathered} \]
两种表示的对偶性
Dualité des deux formes compagnons
控制伴随形式和观测伴随形式中的矩阵结构具有对偶性。具体来说,设控制伴随形式的状态空间表示矩阵为 \(A_c, B_c, C_c, D_c\) , 观测伴随形式的矩阵为 \(A_o, B_o, C_o, D_o\) ,它们之间满足以下关系:
\[ A_o=A_c^{\top}, \quad B_o=C_c^{\top}, \quad C_o=B_c^{\top}, \quad D_o=D_c \]
这表明这两种形式是对偶的。当我们讨论系统的可控性和可观测性时,这种对偶性将会再次出现。通过这种对偶关系,我们可以看到控制和观测问题之间的内在联系,进而帮助我们在系统分析中使用相似的工具和方法。
C2.1.6 状态空间的基变换 Changement de base dans l'espace d'état
状态的表示不是唯一的。对于状态\(x(t)\),假设存在状态\(z(t)\)是\(x(t)\)的线性变换:
\[ x(t)=T z(t) \]
则有:
\[ \begin{gathered}\dot{z}(t)=T^{-1} \dot{x}(t)=T^{-1}(A x(t)+B u(t))=T^{-1} A T z(t)+T^{-1} B u(t) \\y(t)=C x(t)+D u(t)=C T z(t)+D u(t)\end{gathered} \]
因此新的状态:
\[ \left\{\begin{array}{l}\dot{z}(t)=\tilde{A} z(t)+\tilde{B} u(t) \\y(t)=\tilde{C} z(t)+D u(t)\end{array} \quad \text { 其中 } \quad \tilde{A}=T^{-1} A T, \tilde{B}=T^{-1} B, \tilde{C}=C T\right. \]
而此时的外部表示:
\[ \begin{aligned} H(s) & =\tilde{C}(s I-\tilde{A})^{-1} \tilde{B}+D \\ & =C T\left(s I-T^{-1} A T\right)^{-1} T^{-1} B+D \\ & =C\left(T\left(s I-T^{-1} A T\right) T^{-1}\right)^{-1} B+D \\ & =C(s I-A)^{-1} B+D \end{aligned} \]
并不发生改变。
CE2.5 双槽系统 système à 2 cuves

前后两个阀门vanne 分别如下控制。
\[ \frac{d Q_e}{d t}+Q_e=K_V U; Q_s = cst. \]
输出电压为:
\[ V_2=K_c H_2 \]
两个槽中的水量(高度):
\[ \left\{\begin{array}{l} S_1 \frac{d H_1}{d t}=Q_e-\alpha \sqrt{H_1} \\ S_2 \frac{d H_2}{d t}=\alpha \sqrt{H_1}-Q_s \end{array}\right. \]
参考这些方程,我们可以确定\(x = (Q_e,H_1,H_2)\)为状态向量的系统状态表示,但是显然,这并非线性。我们尝试寻找平衡点位置。
\[ \left\{\begin{array} { l } { \overline { Q } _ { e } = K _ { v } \overline { U } } \\{ 0 = \overline { Q } _ { e } - \alpha \sqrt { \overline { H } _ { 1 } } } \\{ 0 = \alpha \sqrt { \overline { H } _ { 1 } } - \overline { Q } _ { s } }\end{array} \rightarrow \left\{\begin{array}{l}\bar{Q}_e=\bar{Q}_s\\\bar{U}=\bar{Q}_e/K_v \\\bar{H}_1=\left(\bar{Q}_e / \alpha\right)^2 \\\bar{H}_2 \text { quelconque }\end{array}\right.\right. \]
然后可以在这一点周围进行线性化。
\[ \sqrt{H_1} \approx \sqrt{\bar{H}_1}+\frac{1}{2 \sqrt{\bar{H}_1}} \tilde{H}_1 \]
得到:
\[ \begin{aligned}& S_1 \frac{d \tilde{H}_1}{d t}=\tilde{Q}_e-\alpha \frac{1}{2 \sqrt{\bar{H}_1}} \tilde{H}_1 \\& S_2 \frac{d \tilde{H}_2}{d t}=\alpha \frac{1}{2 \sqrt{\bar{H}_1}} \tilde{H}_1-\tilde{Q}_s\end{aligned} \]
C2.2 稳定 stabilité
C2.2.1 Lyapunov意义下的稳定 Stabilité au sens de Lyapunov
本节考虑系统:
\[ \begin{aligned}& \dot{x}(t)=f(x(t)), \quad t>0 \\& x(0)=x_0\end{aligned} \]
Lyapunov意义下稳定性的定义
平衡点\(\bar
x\)是稳定的,或者称广义稳定stable au sens large,当且仅当平衡点满足:
\[ \forall \varepsilon>0, \exists \delta=\delta(\varepsilon)>0:\left\|x_0-\bar{x}\right\|<\delta \Rightarrow\|x(t)-\bar{x}\|<\varepsilon, \forall t>0 \]
即,平衡点 \(\bar{x}\) 是(局部)稳定的,当且仅当对于任何足够接近平衡点 \(\bar{x}\)的初始条件 \(x_0\) ,系统的轨迹 \(x(t)\) 在任意 \(t \geq 0\) 时都保持足够接近 \(\bar{x}\) 。

式中的范数一般选择欧几里得范数\(\|x\|=\sqrt{x^{\top} x}\)
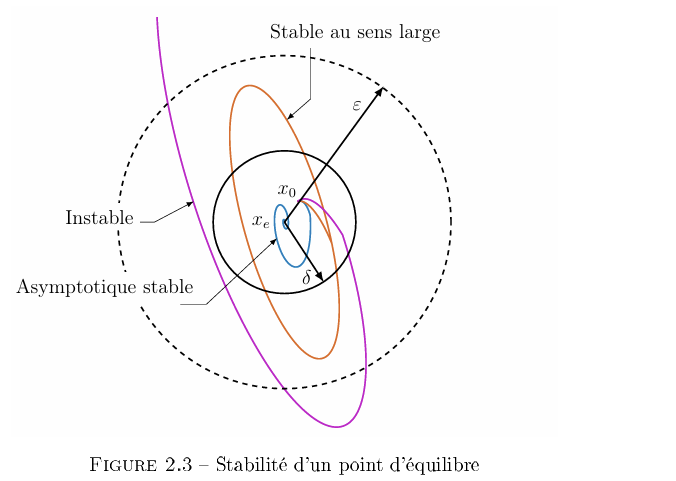
CE2.6 三个针对Lyapunou稳定性的研究
分别讨论\(\dot{x}=-x^3\),\(\dot{x}=x^3\),\(\ddot{z}+\omega^2 z=0\)的稳定性。
对于\(\dot{x}=-x^3\),唯一的平衡点是\(\bar{x}=0\)。写成如下形式直接对两侧积分:
\[ \frac{d x}{x^3}=-d t \]
最终可得\(x(t)=\frac{x_0}{\sqrt{1+2 t x_0^2}}\),其中\(t \geq 0\) 。当\(|x(t)| \leq \varepsilon\)时,有:
\[ \frac{x_0^2}{1+2 t x_0^2} \leq \varepsilon^2 \]
对于任意的\(t \geq 0\) ,上述不等式满足的充分必要条件为\(\left|x_0\right| \leq \varepsilon = \delta\),因此此平衡点是稳定的
对于\(\dot{x}=x^3\),唯一的平衡点为\(\bar{x}=0\) ,同样的方法可以得到:
\[ x(t)=\frac{x_0}{\sqrt{1-2 t x_0^2}} \]
当\(t\)趋近于\(\frac{1}{2 x_0^2}\)时,无论初始条件,\(|x(t)| \rightarrow+\infty\),因此是不稳定的。
对于\(\ddot{z}+\omega^2 z=0\),选择状态向量为\(x=\left(x_1, x_2\right)^{\top}=(z, \dot{z})^{\top}\),有\(f(x) = \left(x_2,-\omega^2 x_1\right)\)。唯一的平衡点为\(\bar x = 0\)。解的:
\[ \begin{aligned}& z(t)=x_{10} \cos (\omega t)+\frac{x_{20}}{\omega} \sin (\omega t) \\& \dot{z}(t)=-\omega x_{10} \sin (\omega t)+x_{20} \cos (\omega t)\end{aligned} \]
有:
\[ \|x(t)\| \leq \sqrt{2}\left(1+\omega+\frac{1}{\omega}\right)\left\|x_0\right\| \]
因此,对于任意的\(\varepsilon\),只要定义\(\delta = \frac{\varepsilon}{\sqrt{2}\left(1+\omega+\frac{1}{\omega}\right)}\),就能使\(\left\|x_0\right\|<\delta \Rightarrow \|x(t)\|<\varepsilon\)对于任意的\(t\)成立。因此是稳定的
渐近稳定性 stabilité asymptotique
为了进一步描述系统的收敛行为,称一个系统为渐进稳定性的当且仅当它是Lyapunov稳定的且满足:
\[ \exists \eta>0:\left\|x_0-\bar{x}\right\|<\eta \Rightarrow \lim _{t \rightarrow+\infty}\|x(t)-\bar{x}\|=0 \]
也就是在稳定的基础上,要求热呢初始条件\(x_0\)取自平衡点的某一个邻域对应的轨迹,最终都收敛到平衡点上。
指数稳定性 stabilité exponentielle
为了进一步表征状态轨迹的收敛速度,引入指数稳定性。称一个平衡点\(\bar x\)为指数稳定的,当且仅当:
\[ \exists \delta, M, \kappa>0:\left\|x_0-\bar{x}\right\|<\delta \Rightarrow\|x(t)-\bar{x}\| \leq M\left\|x_0-\bar{x}\right\| e^{-\kappa t}, \forall t \geq 0 \]
这是一个比Lyapunov稳定和渐进稳定都要更强的稳定性,同时指出了其轨迹的衰减速度可以有指数衰减率\(\kappa\)控制。
以上所有的稳定性都不会受系统的基的影响。
C2.2.2 研究系统在平衡点的稳定性的方法
在之前的例子中,研究系统稳定性依赖于微分方程的解析解。这是十分困难的,在本节中将介绍不求解析解的前提下衡量系统稳定性的方法。
稳定性和偏移量的关系 stabilité et perte
首先,假设\(\bar x\)是系统的一个平衡点,那么\(z = x-\bar x\)在零点处对于系统\(\dot{z}(t)=\tilde{f}(z(t))\)有平衡点。由于稳定性不受基的影响,我们更倾向于在零点处研究稳定性,而非考虑偏移量。
线性时不变系统的稳定性
首先研究线性时不变系统:
\[ \dot{x}(t)=A x(t) \]
我们忽略了偏移量,因此,系统在\(\bar x = 0\)有平衡点,且这个方程的解我们是知道的:
\[ x(t)=e^{A t} x_0 \]
很显然,其解满足\(\|x(t)\| \leq\left\|e^{A
t}\right\|\left\|x_0\right\|, \quad \forall t \geq
0\)。也就是说,线性时不变系统是否稳定,仅取决于\(e^{A
t}\)的诱导系数norme induite de la matrice。
矩阵指数和矩阵的诱导系数
矩阵的特征值
valeur propre,谱spectre,代数重数mutipilicités algébrique和几何重数mutipilicités géométrique
Hurwitz矩阵
定理 1
线性时不变系统是稳定的当且仅当:
- 矩阵A的所有特征值实部都非正:\(\forall \lambda \in \operatorname{sp}(A), \quad \operatorname{Re}(\lambda) \leq 0\)
- 对于所有实部为零的特征值,其代数重数几何重数必须相等
线性时不变系统是渐进/指数稳定的,当且仅当:
- A是Hurwitz 矩阵。
在上述的定理的第二条中,我们间接为渐进稳定和指数稳定构建了等价关系。事实上,对于线性时不变系统,这两种稳定性是等价的。
考虑矩阵指数可以由用特征值 \(\lambda\) 和一个与时间 \(t\) 相关的多项式 \(P_\lambda(t)\) 的线性组合来表示:
\[ e^{A t}=\sum_{\lambda \in \operatorname{sp}(A)} P_\lambda(t) e^{\lambda t} \]
其中, \(P_\lambda(t)\) 的次数最多等于 \(\lambda\) 的代数重数减去 1 。当 \(\lambda\) 的几何重数大于或等于 2 时, \(P_\lambda(t)\) 的次数会小于代数重数减去1,因为特征值的几何重数决定了 Jordan 块的数量。
由此我们可以定义矩阵的谱线横坐标spectral abscissa :
\[ \omega(A)=\max (\operatorname{Re}(\operatorname{sp}(A))) \]
- 对于任意 \(\sigma>\omega(A)\) ,存在常数 \(M_\sigma>0\) ,使得:
\[ \left\|e^{A t}\right\| \leq M_\sigma e^{\sigma t}, \quad \forall t \geq 0 \]
- 对于任意 \(\sigma<\omega(A)\) ,不存在常数 \(M_\sigma>0\) ,使得:
\[ \left\|e^{A t}\right\| \leq M_\sigma e^{\sigma t}, \quad \forall t \geq 0 \]
换句话说,当矩阵 \(A\) 是 Hurwitz
矩阵时, \(\omega(A)\)
表示系统轨迹的最大理论指数衰减速率le taux de décroissance exponentiel maximal。
CE2.7 两个特征值为0的情况
考虑\(A=\left(\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right) \in \mathbb{R}^{2 \times 2}\),唯一的特征值为\(0\),因此不是指数稳定的。此时,\(0\)是一个代数重数为\(2\)的特征值。对于几何重数,\(\operatorname{ker}(\lambda I-A)=\operatorname{ker}(A)=\mathbb{R}^2\),因此几何重数也是\(2\)。因此,系统是稳定的。
考虑\(A=\left(\begin{array}{ll}0 & 1 \\ 0 & 0\end{array}\right) \in \mathbb{R}^{2 \times 2}\),唯一的特征值为\(0\),代数重数为\(2\)。考虑几何重数:\(\operatorname{ker}(\lambda I-A)=\operatorname{ker}(A)=\left\{\left(x_1, 0\right): x_1 \in \mathbb{R}\right\}\),因此几何重数为\(1\)。故系统不是稳定的。
非线性系统:Lyapunov第一方法
定理 3:设 \(f: \mathbb{R}^n \rightarrow \mathbb{R}^n\) ,且对于某个向量 \(\bar{x} \in \mathbb{R}^n , f(\bar{x})=0\) ,其中 \(f\) 是在 \(\bar{x}\) 附近连续可微的向量场。记 \(A=\frac{\partial f}{\partial x}(\bar{x})\) 为在平衡点处 \(f\) 的雅可比矩阵。则系统的平衡点 \(\bar{x}\) 满足以下条件:
- 当且仅当矩阵 \(A\) 是
Hurwitz时,平衡点是指数稳定的:
\[ \forall \lambda \in \operatorname{sp} A, \quad \operatorname{Re}(\lambda)<0 \]
- 如果 \(A\) 存在一个特征值的实部严格为正,则平衡点是不稳定的:
\[ \exists \lambda \in \operatorname{sp} A, \quad \operatorname{Re}(\lambda)>0 \]
Lyapunov
第一方法的优点在于为研究平衡点的指数稳定性提供了一个简单而系统的框架。然而,该方法在处理渐近稳定性问题时缺乏足够的精确性。在一些情况下,Lyapunov
第一方法无法得出结论。此外,我们希望拥有更精细的工具来估计平衡点的吸引域,也就是系统轨迹会收敛到平衡点的初始条件集合。Lyapunov
的第二方法正是为了满足这些需求。但是本笔记不会涉及。
2.2.3 有界输入-有界输出稳定性 Stabilité Entrée Bornée Sortie Bornée (EBSB)
在连续条件下:
- 充要条件 1:
$$
_{-}^{+}|h(t)| d t<+ $$
- 充要条件 2:一个因果系统的传递函数 \(H(s)\) 是 EBSB 稳定的,当且仅当 \(H(s)\) 的所有极点的实部都小于 0 (可以通过 Routh 判据验证)。
如果系统的演化矩阵 \(A\) 是 Hurwitz 的,那么 \(H(s)\) 的所有极点的实部都小于 0 。然而,反过来不一定成立。
Routh-Hurwitz判据
C2.3 可控性 commandabilité
C2.3.1 定义
可控性概念是系统控制中的一个基本概念,描述我们通过控制输入在状态空间中操纵系统的能力。 本节仅讨论线性时不变系统:
\[ \dot{x}(t)=A x(t)+B u(t) \]
其积分形式为:
\[ x\left(t_2\right)=e^{A\left(t_2-t_1\right)} x\left(t_1\right)+\int_{t_1}^{t_2} e^{A\left(t_2-\tau\right)} B u(\tau) d \tau, \quad \forall t_1<t_2 \]
定义
- 称在时间 \(T>0\) 内从 \(x_I \in \mathbb{R}^n\) 到 \(x_F \in \mathbb{R}^n\) 可控,当且仅当存在一个 \(u \in L^2(0, T)\) ,使得在初始条件 \(x(0)=x_I\) 下,轨迹满足 \(x(T)=x_F\) ,即:
\[ x_F=e^{A T} x_I+\int_0^T e^{A(T-\tau)} B u(\tau) d \tau \]
- 称系统可控, 当它在任意时间 \(T>0\) 内从任意 \(x_I \in \mathbb{R}^n\) 到任意 \(x_F \in \mathbb{R}^n\)可控;
- 反之,则称之为不可控。
也就是说,一个系统是完全可控的,如果存在一个控制输入 \(\mathbf{u}(t)\) ,可以使系统在有限时间内从任意初始状态 \(\mathbf{x}_0\) 转移到任意最终状态 \(\mathbf{x}_1\) 。
CE2.8 可控性的例子
考虑由以下状态方程定义的单变量系统,维度为 \(n=2\) :
\[ \dot{x}(t)=\left(\begin{array}{cc} a_1 & a_3 \\ 0 & a_2 \end{array}\right) x(t)+\binom{b_1}{0} u(t) \]
其中假设 \(b_1 \neq 0\) 。直观上可以感觉到,由于 \(b_1 \neq 0\) ,状态变量 \(x_1\) 受控制输入 \(u(t)\) 的影响,因为它的演化由以下方程控制:
\[ \dot{x}_1(t)=a_1 x_1(t)+a_3 x_2(t)+b_1 u(t) \]
事实上,通过设定控制输入 \(u(t)=\frac{1}{b_1}\left(-a_1 x_1(t)-a_3 x_2(t)+v(t)\right)\) ,可以得到 \(\dot{x}_1(t)=v(t)\) 。接着,设定 \(v(t)=\frac{\beta-\alpha}{T}\) ,其中 \(\alpha, \beta \in \mathbb{R}\) ,且 \(T>0\) 是任意的,则可以实现 \(x_1(0)=\alpha\) 和 \(x_1(T)=\beta\) 。因此,状态 \(x_1\) 是可控的。
至于状态变量 \(x_2\) 的演化由方程 \(\dot{x}_2(t)=a_2 x_2(t)\) 决定。因此,它是自治的,既不依赖于控制输入 \(u\) ,也不依赖于可控状态变量 \(x_1\) 。无论选择什么控制输入 \(u(t)\) ,其最终状态都不能任意选择。因此,该系统是不可控的。
C2.3.2 线性时不变系统的可控性
Kalman 可控性判据
对于 \((A, B) \in \mathbb{R}^{n \times n} \times \mathbb{R}^{n \times m}\) ,当且仅当可控性矩阵
\[ \mathcal{C}=\left(\begin{array}{lllll} B & A B & A^2 B & \ldots & A^{n-1} B \end{array}\right) \in \mathbb{R}^{n \times n m} \]
满秩时,系统是可控的。也就是说, \(\mathcal{C}\) 的秩等于 \(n\) ,即 \(\operatorname{Rang}(\mathcal{C})=n\)
Matlab
CE2.9 Kalman盘踞的示例
对于状态方程:
\[ \begin{aligned}& \dot{\mathbf{x}}(t)=\left[\begin{array}{cc}-1 & 2 \\1 & -2\end{array}\right] \mathbf{x}(t)+\left[\begin{array}{c}1 \\-1\end{array}\right] u(t) \\& y(t)=\left[\begin{array}{ll}1 & 0\end{array}\right] \mathbf{x}(t)\end{aligned} \]
其可控性矩阵:
\[ \mathbf{Q}_C=\left[\begin{array}{ll}B & A B\end{array}\right]=\left[\begin{array}{cc}1 & -3 \\-1 & 3\end{array}\right] \]
的秩为\(1\),因此系统是部分可控partiellement commandable的
C2.3.3 Kalman 控制标准形式、系统可稳定性概念与 PBH 判据 Forme canonique de Kalman pour la commande, notion de système stabilisable et test PBH
我们刚刚提到了部分可控的概念,实际上,部分可控描述了满足:
\[ \operatorname{rang}(\mathcal{C})=q, \quad \text { 其中 } \quad 0 \leq q<n \]
的不可控系统。本节中我们尝试研究,这些不可控的系统,它是否在现有状态下仍能被视为“足够”稳定或可控?
Kalman 控制标准形式 Forme canonique de Kalman pour la commande
这种形式考虑将系统的状态空间划分为\(q\)维的完全可控部分和\(n-q\)维的不可控部分。
考虑状态空间表示:
\[ \begin{aligned}\dot{x}(t) & =A x(t)+B u(t) \\y(t) & =C x(t)+D u(t)\end{aligned} \]
当\((A,B)\)不可控时,存在变换(换基):
\[ z=\binom{z_c}{z_{\bar{c}}}=T x, \quad z_c \in \mathbb{R}^q, \quad z_{\bar{c}} \in \mathbb{R}^{n-q} \]
其中\(T \in \mathbb{R}^{n \times n}\)可逆,使得系统可以被重新表示为:
\[ \begin{aligned}& \dot{z}=\left(\begin{array}{cc}\tilde{A}_c & \tilde{A}_{12} \\0 & \tilde{A}_{\bar{c}}\end{array}\right) z+\binom{\tilde{B}_c}{0} u \\& y=\left(\begin{array}{cc}\tilde{C}_c & \tilde{C}_{\bar{c}}\end{array}\right) z+D u\end{aligned} \]
而其中\(\left(\tilde{A}_c, \tilde{B}_c\right) \in \mathbb{R}^{q \times q} \times \mathbb{R}^{q \times m}\)是完全可控的,且传递函数满足:
\[ H(s)=C(s I-A)^{-1} B+D=\tilde{C}_c\left(s I-\tilde{A}_c\right)^{-1} \tilde{B}_c+D \]
Matlab
在表述为Kalman标准控制形式之后,将:
- \(\tilde{A}_c\)的特征值称为可控模态
commandables - \(\tilde{A}_{\bar{c}}\)的特征值称为不不可控模态
non commandables
CE2.10 不可控系统的分解
考虑系统:
\[ \binom{\dot{x}_1(t)}{\dot{x}_2(t)}=\left(\begin{array}{cc}-1 & 0 \\0 & -1\end{array}\right)\binom{x_1(t)}{x_2(t)}+\binom{1}{1} u(t) \]
其可控性矩阵:
\[ [\mathbf{B}: \mathbf{A B}]=\left(\begin{array}{l:l}1 & -1 \\1 & -1\end{array}\right) \]
的秩为\(1\),因此是部分可控的。为此,我们可以进行换基,注意换基的方法并不唯一:
\[ \mathbf{T}=\left(\begin{array}{l:l} 1 & 1 \\ 1 & 0 \end{array}\right) \text { ou } \quad \mathbf{T}=\left(\begin{array}{ll} 1 & 0 \\ 1 & 1 \end{array}\right) \text { ou } \ldots \]
在这两种情况下可以得到新的状态:
\[ \binom{\dot{\bar{X}}_1(t)}{\dot{\bar{X}}_2(t)}=\left(\begin{array}{c:c} -1 & 0 \\ 0 & -1 \end{array}\right)\binom{\bar{x}_1(t)}{\bar{X}_2(t)}+\binom{1} u(t) \]
PBH 判据
设 \((A, B) \in \mathbb{R}^{n \times n} \times \mathbb{R}^{n \times m}\) 为一对矩阵。
- 当且仅当满足以下条件时,矩阵对 \((A, B)\) 是可控的:
\[ \forall \lambda \in \mathbb{C}, \forall x \in \mathbb{C}^n, \quad\left[x^* A=\lambda x^* \text { 且 } x^* B=0\right] \Rightarrow x=0 \]
- 如果矩阵对 \((A, B)\) 是不可控的,则不可控的特征值 \(\lambda \in \mathbb{C}\) 满足:
\[ \exists x \in \mathbb{C}^n \backslash\{0\}: x^* A=\lambda x^* \text { 且 } x^* B=0 \]
或者说,在连续条件下,矩阵对 \((A, B)\) 是可控的等价于:
- 对于所有 \(s \in \mathbb{C}\) , \(\operatorname{rang}[s I-A \quad B]=n\) ;
- 对于所有 \(\lambda \in \operatorname{spectre}(A) , \operatorname{rang}\left[\begin{array}{ll}\lambda I-A & B\end{array}\right]=n_{\text {。 }}\)
通过第二个条件,可以判断哪些特征值是不可控的,对于这些特征值,第二个条件不成立。
可稳定性 stabilisable
对于使用上述方法判断的不可控的特征值,如果其实部小于零\(\operatorname{Re}(\lambda)<0\),则称系统是可稳定的。
CE2.11 PBH的应用
考虑矩阵,其中\(b_1 \neq 0 \text { 且 } a_1 \neq a_2\):
\[ A=\left(\begin{array}{cc} a_1 & a_3 \\ 0 & a_2 \end{array}\right), \quad B=\binom{b_1}{0} \]
在先前的例子中,我们用朴素的方法说明了其整体来说不可控。也可以通过可控性矩阵:
\[ \operatorname{Rang} \mathcal{C}=\operatorname{Rang}\left(\begin{array}{cc} b_1 & a_1 b_1 \\ 0 & 0 \end{array}\right)=1<n=2 \]
判断出其部分可控。我们产生过hi应用\(PBH\)。首先考虑:
\[ x^* A=a_1 x^* , \ x^* B=0 \]
第二个式子可以直接给出\(x^*_1 = 0\),而第一个方程展开之后:
\[ \left(0, x^*_2\right)\left(\begin{array}{cc}a_1 & a_3 \\0 & a_2\end{array}\right)=a_1\left(0, x^*_2\right) \]
可得:
\[ \left(0, x^*_2 a_2\right)=\left(0, a_1 x^*_2\right) \]
由此,可得\(x^* = 0\),对于\(a_1\)是可控模态。同理,对于\(a_2\),在此不再赘述,可以得到\(x^*_2=(0,1) \neq 0\),因此不可控。
C2.4 可观性 observabilité
可观性描述能否通过观测输出\(y\)和已知的输入\(u\)来重构系统的状态\(x\)。在本节中,考虑线性时不变系统:
\[ \begin{aligned}\dot{x}(t) & =A x(t)+B u(t) \\y(t) & =C x(t)+D u(t)\end{aligned} \]
我们可以观测输出\(y(t)\),已知\(u(t),A,B,C,D\)。
C2.4.1 可观性的定义
称系统,或称矩阵对\((A,C)\)是可观的,当对于任何时间\(T>0\) ,所有初始条件 \(x_{10}, x_{20} \in \mathbb{R}^n\) 以及任意输入 \(u \in L^2(0, T)\) ,记 \(y_i(t)\) 为在初始条件 \(x_{i 0}\) 和输入 \(u\) 下系统的输出,则 \(y_1(t)=y_2(t)\) 对于所有 \(t \in[0, T]\) 成立时,必然有 \(x_{10}=x_{20}\)。也就是说:
\[ \left[C e^{A t} x_{10}=C e^{A t} x_{20}, \forall t \in[0, T]\right] \Rightarrow x_{10}=x_{20} \]
CE2.12 二维系统的可观性
考虑单变量系统:
\[ \begin{aligned}& \dot{x}(t)=\left(\begin{array}{cc}a_1 & 0 \\a_3 & a_2\end{array}\right) x(t)+\binom{b_1}{b_2} u(t) \\& y(t)=\left(\begin{array}{ll}1 & 0\end{array}\right) x(t)\end{aligned} \]
显然的是,对于任意的两个相同的输出,我们不能确定\(x_2\)是否相同,因此系统不可观。
C2.4.2 可观性的判定
Kalman 可观性判据
称矩阵对\((A,C)\in \mathbb{R}^{n \times n} \times \mathbb{R}^{p \times n}\)是可观的,当且仅当可观性矩阵:
\[ \mathcal{O}=\left(\begin{array}{c} C \\ C A \\ C A^2 \\ \vdots \\ C A^{n-1} \end{array}\right) \in \mathbb{R}^{n p \times n} \]
是满秩的,即\(\operatorname{Rang}(\mathcal{O})=n\)。
Matlab
CE2.13 使用Kalman可观性判据计算可观性的例子
对于系统:
\[ \begin{aligned}& \dot{\mathbf{x}}(t)=\left[\begin{array}{cc}0 & 1 \\-2 & -3\end{array}\right] \mathbf{x}(t)+\left[\begin{array}{l}0 \\1\end{array}\right] u(t) \\& y(t)=\left[\begin{array}{ll}1 & 1\end{array}\right] \mathbf{x}(t)\end{aligned} \]
其可观性矩阵:
\[ \mathbf{Q}_o=\left[\frac{\mathbf{C}}{\mathbf{C A}}\right]=\left[\begin{array}{cc}1 & 1 \\-2 & -2\end{array}\right] \]
其秩为\(1\),称系统部分客观
partiellemnet observable。
CE2.4.3 Kalman 观测标准形式,系统可检测性和PBH判据 Forme canonique de Kalman pour l'observation, notion de sys
tème détectable et test PBH
在之前的例子中,我们提到了部分客观性,即满足以下条件的系统:
\[ \operatorname{rang}(\mathcal{O})=q, \quad \text { 其中 } \quad 0 \leq q<n \]
本节将讨论这种系统。
Kalman 观测标准形式
定理:设 \((A, C) \in \mathbb{R}^{n \times n} \times \mathbb{R}^{p \times n}\) 为不可观对。则存在一个变换:
\[ z=\binom{z_o}{z_{\bar{o}}}=T x, \quad z_o \in \mathbb{R}^q, \quad z_{\bar{o}} \in \mathbb{R}^{n-q} \]
其中 \(T \in \mathbb{R}^{n \times n}\) 是可逆矩阵,使得系统可以重写为:
\[ \begin{aligned} & \dot{z}=\left(\begin{array}{cc} \tilde{A}_0 & 0 \\ \tilde{A}_{21} & \tilde{A}_{\bar{o}} \end{array}\right) z+\binom{\tilde{B}_o}{\tilde{B}_{\bar{o}}} u \\ & y=\left(\begin{array}{cc} \tilde{C}_o & 0 \end{array}\right) z+D u \end{aligned} \]
其中 \(\left(\tilde{A}_o, \tilde{C}_o\right) \in \mathbb{R}^{q \times q} \times \mathbb{R}^{p \times q}\) 是可观的,且传递函数为:
\[ H(s)=C(s I-A)^{-1} B+D=\tilde{C}_o\left(s I-\tilde{A}_o\right)^{-1} \tilde{B}_o+D \]
Matlab
其中,
- \(\tilde{A}_o\) 的特征值称为可观模态。
- \(\tilde{A}_{\bar{o}}\) 的特征值称为不可观模态。
PBH 可观性判据
- 矩阵对 \((A, C)\) 是可观的,当且仅当:
\[ \forall \lambda \in \mathbb{C}, \forall x \in \mathbb{C}^n, \quad[A x=\lambda x \text { 且 } C x=0] \Rightarrow x=0 \]
- 如果矩阵对 \((A, C)\) 是不可观的,则不可观的特征值 \(\lambda \in \mathbb{C}\) 满足:
\[ \exists x \in \mathbb{C}^n \backslash\{0\}: A x=\lambda x \text { 且 } C x=0 \]
更进一部分,矩阵对 \((A, C)\) 是可观的等价于以下任意一条:
- 对于所有 \(s \in \mathbb{C}\) ,有 \(\operatorname{rang}\left[\begin{array}{c}s I-A \\ C\end{array}\right]=n\) 。
- 对于所有 \(\lambda \in \operatorname{spectre}(A)\) ,有 \(\operatorname{rang}\left[\begin{array}{c}\lambda I-A \\ C\end{array}\right]=n\) 。
系统可检测性 détectable
对于矩阵对 \((A, C) \in \mathbb{R}^{n \times n} \times \mathbb{R}^{p \times n}\) ,如果其所有不可观的模态的特征值 \(\lambda \in \mathbb{C}\) 满足 \(\operatorname{Re}(\lambda)<0\) ,则称该系统为可检测的。换句话说,基于 PBH 判据, \((A, C)\) 是可检测的,当且仅当:
\[ \forall \lambda \in \mathbb{C}, \forall x \in \mathbb{C}^n \backslash\{0\},[A x=\lambda x \text { 且 } C x=0] \Rightarrow \operatorname{Re}(\lambda)<0 \]
这意味着,系统中不可观的模态如果对应的特征值实部为负,则该系统是可检测的。
CE2.14 倒立摆问题
回忆线性化之后的矩阵:
\[ A=\left(\begin{array}{cccc}0 & 0 & 1 & 0 \\0 & 0 & 0 & 1 \\0 & \frac{m g}{M} & 0 & 0 \\0 & \frac{(m+M) g \cos \bar{x}_2}{M} & 0 & 0\end{array}\right), \quad C=\left(\begin{array}{llll}0 & 1 & 0 & 0\end{array}\right) \]
计算得可观测矩阵的秩为:
\[ q=\operatorname{Rang} \mathcal{O}=\operatorname{Rang}\left(\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & \frac{(m+M) g \cos \bar{x}_2}{M l} & 0 & 0 \\ 0 & 0 & 0 & \frac{(m+M) g \cos \bar{x}_2}{M l} \end{array}\right)=2 \]
由此,可观子空间的维数为\(2\),不可观子空间的维数为\(2\)。
首先考虑矩阵A的特征值:\(\{0,0,\sqrt{\frac{(m+M) g}{M l}},-\sqrt{\frac{(m+M) g}{M l}}\}\)。
对于特征值为\(0\)的情况,当\(x=(1,0,0,0)^{\top} \neq 0\),有\(A x=0, \quad C x=0\),因此特征值\(0\)不可观。
对于后两种情况,以\(\lambda =\sqrt{\frac{(m+M) g}{M l}}\)为例,方程组:
\[ x_3=\lambda x_1, \quad x_4=\lambda x_2, \quad \frac{m g}{M} x_2=\lambda x_3, \quad \frac{(m+M) g \cos \bar{x}_2}{M l} x_2=\lambda \]
唯一的解为\(x = 0\),因此\(\lambda\)可观。
C2.5 Kalman标准型 Forme canonique de Kalman
定理: 设 \(A \in \mathbb{R}^{n \times n} 、 B \in \mathbb{R}^{n \times m} 、 C \in \mathbb{R}^{p \times n} 、 D \in \mathbb{R}^{p \times m}\) 。存在一个可逆变换 \(T \in \mathbb{R}^{n \times n}\) ,使得系统可以重写为:
\[ z=\left(\begin{array}{c}z_{c o} \\z_{c\bar{o}} \\z_{\bar{c} o} \\z_{\overline{c o}}\end{array}\right)=T x \]
变换后,系统的状态方程变为:
\[ \begin{aligned}& \dot{z}=\left(\begin{array}{cccc}\tilde{A}_{c o} & 0 & \tilde{A}_{13} & 0 \\\tilde{A}_{21} & \tilde{A}_{c \bar{o}} & \tilde{A}_{23} & \tilde{A}_{24} \\0 & 0 & \tilde{A}_{\bar{c} o} & 0 \\0 & 0 & \tilde{A}_{43} & \tilde{A}_{\overline{c o}}\end{array}\right) z+\left(\begin{array}{c}\tilde{B}_{c o} \\\tilde{B}_{c \bar{o}} \\0 \\0\end{array}\right) u \\& y=\left(\begin{array}{llll}\tilde{C}_{c o} & 0 & \tilde{C}_{\bar{c} o} & 0\end{array}\right) z+D u\end{aligned} \]
使得:
\(\left(\left(\begin{array}{cc}\tilde{A}_{c o} & 0 \\\tilde{A}_{21} & \tilde{A}_{c \bar{o}}\end{array}\right),\binom{\tilde{B}_{c o}}{\tilde{B}_{c \bar{o}}}\right)\) 可控
\(\left(\begin{array}{cc}\left(\begin{array}{cc}\tilde{A}_{c o} & \tilde{A}_{13} \\0 & \tilde{A}_{\bar{c} o}\end{array}\right),\left(\begin{array}{ll}\tilde{C}_{c o} & \tilde{C}_{\bar{c} o}\end{array}\right)\end{array}\right)\)可观
传递函数为:
\[ H(s)=C(s I-A)^{-1} B+D=\tilde{C}_{c o}\left(s I-\tilde{A}_{c o}\right)^{-1} \tilde{B}_{c o}+D \]
如此,
- \(z_{c o}\) 是系统的可控且可观部分——系统的可控且可观模态是 \(\tilde{A}_{c o}\) 的特征值;
- \(z_{c \bar{o}}\) 是系统的可控但不可观部分——系统的可控但不可观模态是 \(\tilde{A}_{c \bar{o}}\)的特征值;
- \(z_{\bar{c} o}\) 是系统的不可控但可观部分——系统的不可控但可观模态是 \(\tilde{A}_{\bar{c} o}\)的特征值;
- \(z_{\overline{c o}}\) 是系统的不可控且不可观部分——系统的不可控且不可观模态是 \(\tilde{A}_{\overline{c o}}\) 的特征值。
C2.6 可观/可控对偶性 Dualité commandabilité-observabilité
之前我们讨论了系统的对偶性,然后现在我们进一步对偶性与可观/可控性的联系。
对于矩阵对 \((A, C)\) ,如果系统可观,那么其转置系统 \(\left(A^{\top}, C^{\top}\right)\) 可控,反之亦然。这意味着可控性和可观性之间存在对偶关系。
具体来说, 系统
\[ \begin{aligned} & \dot{x}(t)=A x(t)+B u(t) \\ & y(t)=C x(t)+D u(t) \end{aligned} \]
的可控性等价于以下系统的可观性:
\[ \begin{aligned} & \dot{x}(t)=A^{\top} x(t)+C^{\top} u(t) \\ & y(t)=B^{\top} x(t)+D^{\top} u(t) \end{aligned} \]
这表明,一个系统的可控性问题可以转化为其对偶系统的可观性问题,反之亦然。