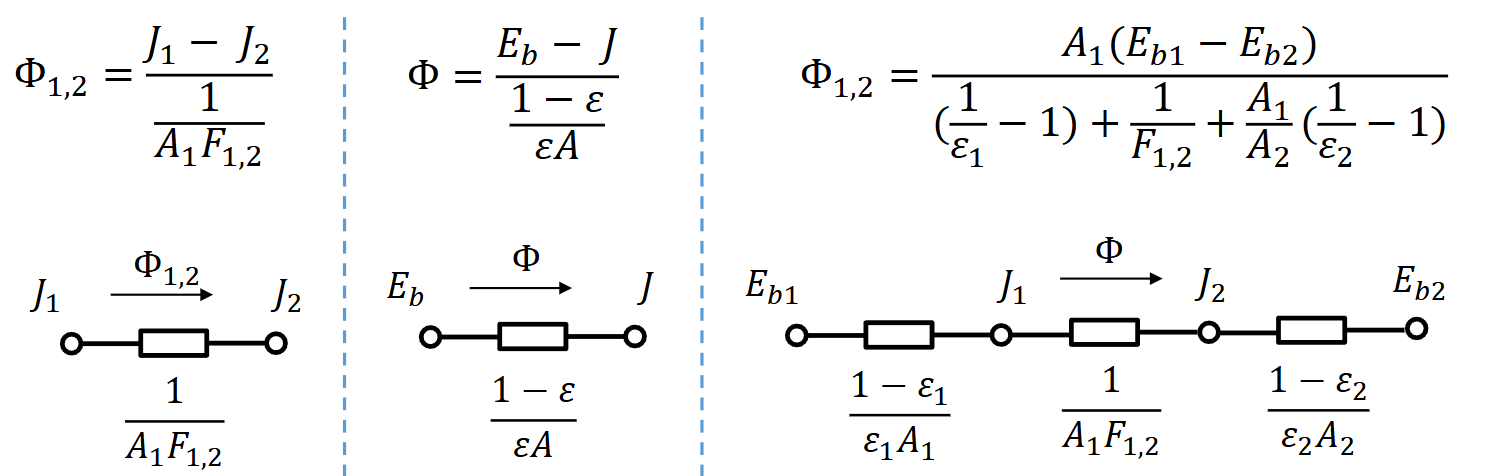热交换器，热辐射 échangeur, rayonnement
热交换器，热辐射 échangeur, rayonnement
热交换器 échangeur
热交换器是一种将热流从热流体传递到冷流体的系统。一般来说其中包含的传热包括对流和传导。
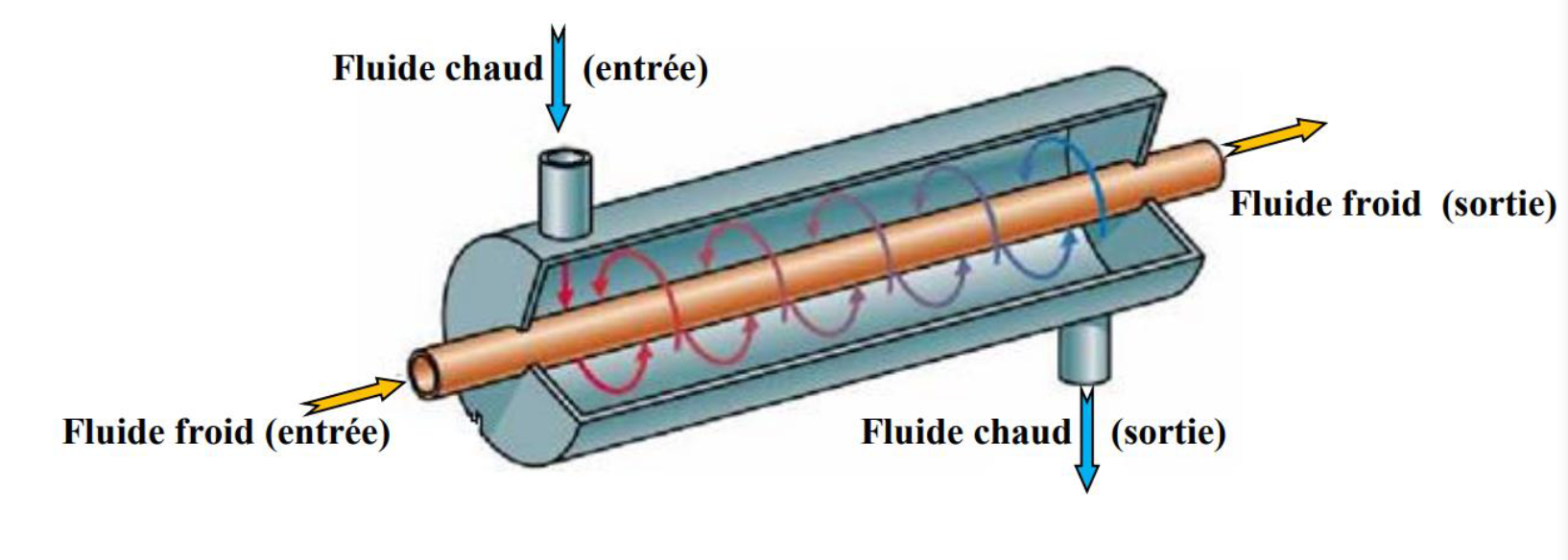
同轴管式换热器 Echangeur tubulaires coaxiaux
整体热交换系数 U Coefficient global d’échange thermique U
\[ \mathrm{d} \Phi=U\left(T_c-T_f\right) d \mathrm{~A} \]
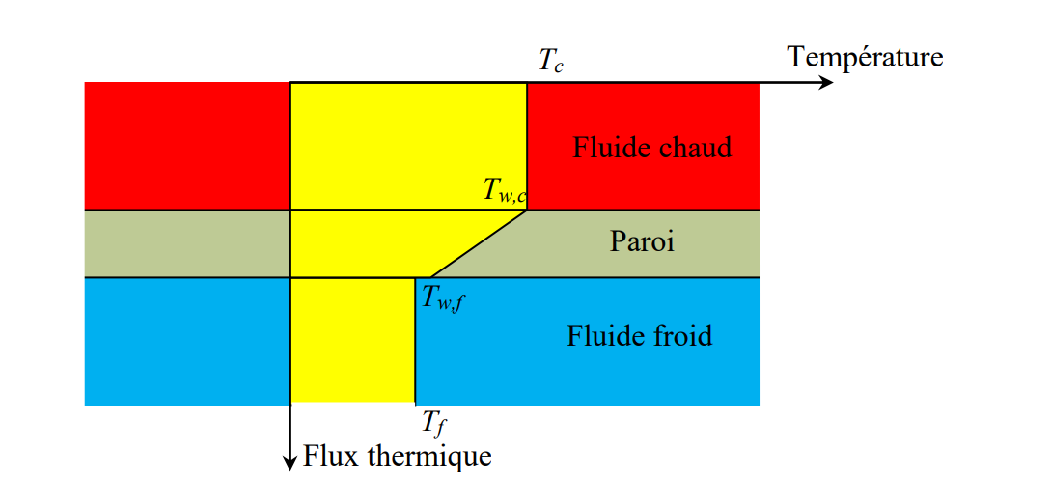
对于图示的交换器，可以如此计算：
\[ \Phi=\frac{T_c-T_f}{\frac{1}{h_c A}+\frac{e}{\lambda A}+\frac{1}{h_f A}} \quad \Phi=U A\left(T_c-T_f\right) \quad \Rightarrow \quad U=\frac{1}{\frac{1}{h_c}+\frac{e}{\lambda}+\frac{1}{h_f}} \]
接下来，我们以通州管式换热器为例研究在此换热器中两种流体流向相反的原因：
考虑热流：
\[ \Phi=\int_e^sU\left(T_c-T_f\right) d \mathrm{~A} = UA\int_e^sT_c(z)-T_f(z)dz \]
因此我们尽可能希望在整个换热器中，温差尽可能大。
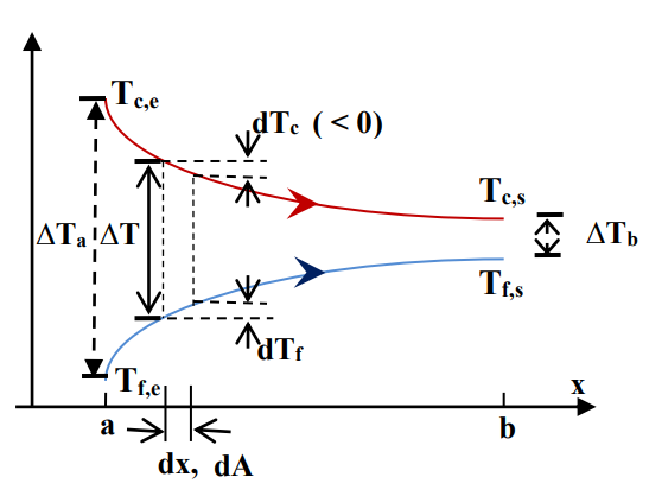
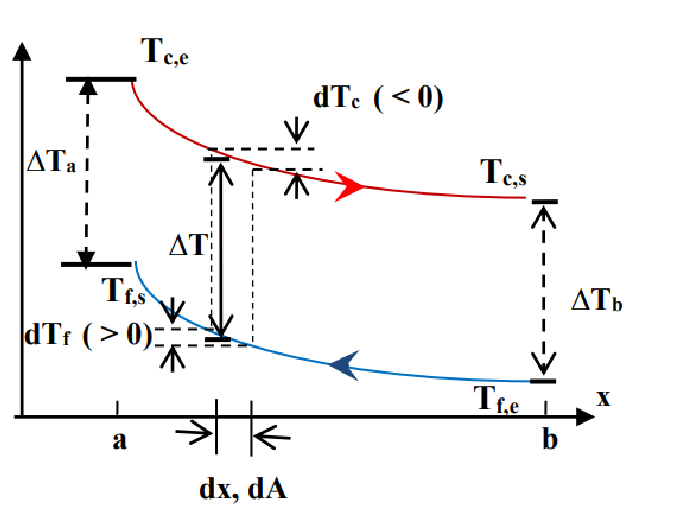
我们可以使用对数平均温差DTLM表示后一项的积分，对于同流Co-courant换热器：
\[ \Phi=U \mathrm{~A} \frac{\left(T_{c, s}-T_{f, s}\right)-\left(T_{c, e}-T_{f, e}\right)}{\ln \left(\frac{T_{c, s}-T_{f, s}}{T_{c, e}-T_{f, e}}\right)}=U \mathrm{~A} \frac{\Delta T_b-\Delta T_a}{\ln \left(\frac{\Delta T_b}{\Delta T_a}\right)} \]
对于逆流Contre-courant换热器：
\[ \Phi=U \mathrm{~A} \frac{\left(T_{c, e}-T_{f, s}\right)-\left(T_{c, s}-T_{f, e}\right)}{\ln \left(\frac{T_{c, e}-T_{f, s}}{T_{c, s}-T_{f, e}}\right)}=U \mathrm{~A} \Delta T_{L M}=U \mathrm{~A} \frac{\Delta T_a-\Delta T_b}{\ln \left(\frac{\Delta T_a}{\Delta T_b}\right)} \]
可以代入一组数据比较两种情况下的\(\Delta T_{L M}\)：
\[ \Delta T_{L M} = \frac{\Delta T_b-\Delta T_a}{\ln \left(\frac{\Delta T_a}{\Delta T_b}\right)} \]
\[ \begin{gathered}T_{c, e}=100^{\circ} \mathrm{C}, T_{c, s}=45^{\circ} \mathrm{C} \\T_{f, e}=15^{\circ} \mathrm{C}, T_{f, S}=30^{\circ} \mathrm{C}\end{gathered} \]
易见，逆流换热器有更高的DTLM，故有更高的效率。
为了修正DTLM假设带来的误差，引入修正因子Facteur de correction\(F\)：
\[ \Phi=U A F \Delta \mathrm{T}_{\mathrm{LM}} \]
换热效率 Efficacité d’un échangeur
\[ \varepsilon = \frac{\Phi_{réel}}{\Phi_{max}} \]
其中，最大热流 Flux maximum possible：
\[ \Phi_{\max }=C_{\min }\left(T_{c, e}-T_{f, e}\right) \]
\(C_{min}\)取\(C_f\)和\(C_c\)的最小值。
NUT方法 méthode NUT
\[ \begin{aligned} & \operatorname{NUT}_c=\frac{U \mathrm{~A}}{C_c} \ \ \ \ & \mathrm{NUT}_f=\frac{U \mathrm{~A}}{C_f} \end{aligned} \]
对于同流：
\[ \varepsilon=\frac{1-\mathrm{e}^{\left[-N U T\left(1+C_r\right)\right]}}{1+C_r} \]
对于逆流：
\[ \varepsilon=\frac{1-\mathrm{e}^{\left[-N U T\left(1-C_r\right)\right]}}{1-C_r \mathrm{e}^{\left[-N U T\left(1-C_r\right)\right]}} \]
热辐射 Rayonnement
热辐射是一种通过发射和接收电磁波来交换热量的方式。
- 电磁能量 Energie électro-magnétique（光子）由物质自发地发射。
- 发射 Emission：热能转换为辐射能（光子）的过程。
- 吸收 Absorption：辐射能反向转换为热能的过程。
波动理论和粒子理论
\[ c = \nu \lambda \ \ \ W = h\nu \]
电磁辐射的光谱区域\([0.1-100\mu m]\)
吸收，反射和穿透 Absorption, Réflexion, Transmission
\[ 1=\frac{Q_\rho}{Q}+\frac{Q_\tau}{Q}+\frac{Q_\alpha}{Q} \]
- 反射率 \(\rho=\frac{Q_\rho}{Q}\)，透射率\(\tau=\frac{Q_\tau}{Q}\)，吸收率\(\alpha=\frac{Q_\alpha}{Q}\)
- 对于固体和流体，透射近似为零
- 对于气体反射近似为零
- 透明介质 Milieu transparent
- 非透明介质 Milieu opaque
对于黑体，吸收率为1。
表面辐射通量 Flux radiatif surfacique
\[ \varphi=\frac{d \Phi}{d A} \]
对于特定的颜色，有单色表面辐射通量Flux surfacique monochromatique \(\varphi_\lambda^R\)：
\[ \varphi^R=\int_{\lambda=0}^{\lambda=\infty} d \varphi_\lambda^R \]
对于非透明介质，实际的通量是入射辐射与反射辐射之差：
\[ \varphi^R=\varphi^e-\varphi^a \]
黑体热辐射的公式
斯忒藩-玻尔兹曼定律 Loi de Stefan-Boltzmann
\[ \varphi_b^e=\sigma T^4 \ \ avec \ \ \sigma=5.67 \times 10^{-8} w /\left(\mathrm{m}^2 . K^4\right) \]
普朗克定律 Loi de Planck
\[ \varphi_{b, \lambda}^e=\frac{C_1 \lambda^{-5}}{\exp \left(\frac{C_2}{\lambda T}\right)-1} \ \ avec \ \ \ \ \begin{aligned}\begin{aligned} & C_1: 3.742 \times 10^{-16} \mathrm{~W} \cdot \mathrm{m}^2 \\ & C_2: 1.4388 \times 10^{-2} \mathrm{~m} \cdot k \end{aligned}\end{aligned} \]
两定律之间的关系
\[ \varphi_b^e=\int_0^{\infty} \varphi_{b, \lambda}^e d \lambda=\int_0^{\infty} \frac{C_1 \lambda^{-5}}{\exp \left(\frac{C_2}{\lambda T}\right)-1} d \lambda \]
黑体辐射定律
\[ \begin{aligned} F_{b(0-\lambda)}=\frac{\int_0^\lambda \varphi_{b, \lambda}^e d \lambda}{\sigma T^4} =\int_0^\lambda \frac{C_1(\lambda T)^{-5}}{\exp \left(\frac{C_2}{\lambda T}\right)-1} \frac{1}{\sigma} d(\lambda T)=f(\lambda T)\end{aligned} \]
\[ \varphi_{\left(\lambda_1-\lambda_2\right)}^e=F_{b\left(\lambda_1-\lambda_2\right)} \varphi_b^e=\left(F_{b\left(0-\lambda_2\right)}-F_{b\left(0-\lambda_1\right)}\right) \varphi_b^e \]
维也纳定律 Loi de Wien
\[ \lambda_{\max } T=2.898 \times 10^{-3} \text { (m.k) } \]
黑体辐射光谱的峰值波长\(\lambda_{max}\)。
兰伯特定律 Loi de Lambert
\[ I_b=\frac{d \Phi(\theta)}{d A \cos \theta \cdot d \Omega} \]
\[ \varphi_b^e=\int_{\Omega=2 \pi} \frac{d \Phi(\theta)}{d A}=I_b \int_{\Omega=2 \pi} \cos \theta d \Omega=I_b \pi \]
一般固液热辐射性质
发射率 Emissivité
\[ \varepsilon=\frac{\varphi^e}{\varphi_b^e}=\frac{E}{E_b}\Leftrightarrow\varphi^e=\varepsilon \varphi_b^e=\varepsilon \sigma T^4 \]
单色发射率 Emissivité monochromatique
\[ \begin{aligned}& \varepsilon_\lambda=\frac{\varphi_\lambda^e}{\varphi_{b \lambda}^e} \Leftrightarrow \varepsilon=\frac{\varphi^e}{\varphi_b^e}=\frac{\int_0^{\infty} \varepsilon_\lambda \varphi_{b \lambda}^e d \lambda}{\sigma T^4}\end{aligned} \]
方向发射率 Emissivité directionnelle
\[ \varepsilon^{\prime}=\frac{I(\theta)}{I_b}=\frac{L^{\prime}}{L^0} \]
其中，\(L'\)被称为方向亮度。
\[ \begin{gathered}\varepsilon=\frac{\varphi^e}{\varphi_b^e}=\frac{I_b \int_{\Omega=2 \pi} \varepsilon_\theta d \Omega}{\pi I_b}=\frac{\int_{\Omega=2 \pi} \varepsilon_\theta d \Omega}{\pi}\end{gathered} \]
吸收率 absorptivité
\[ \alpha_\lambda=\frac{\varphi_\lambda^a}{\varphi_\lambda^i}=\frac{\text { Flux absorbé }}{\text { Flux incident }} \]
从\(2\)中发射出的光被\(1\)吸收的吸收率：
\[ \alpha_1=\frac{\int_0^{\infty} \alpha_\lambda\left(\lambda, T_1\right) \varepsilon_\lambda\left(\lambda, T_2\right) \varphi_{b \lambda}\left(T_2\right) d \lambda}{\int_0^{\infty} \varepsilon_\lambda\left(\lambda, T_2\right) \varphi_{b \lambda}\left(T_2\right) d \lambda} \]
灰体 corps gris
\[ \alpha_\lambda=\alpha=\text { cte } \]
基尔霍夫定律 Loi de Kirchhoff
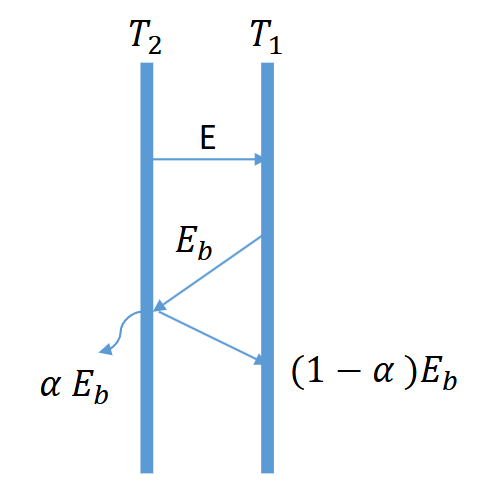
\[ \varphi^R=\varphi^e-\varphi^a=E-\alpha \frac 1\varepsilon E \]
在热平衡时，\(\alpha=\varepsilon\)。
辐射换热计算 Calcul d’échange par rayonnement
形状因子 Facteur de forme
\[ \begin{aligned}& \text { Facteur de Forme } F_{i j}=\frac{\Phi_{\text {partant de } s_i}^{\text {incident sur } s_j}}{\Phi_{\text {partant de } s_i}} \quad \Phi_{\text {partant de } s_i}=S_i \varphi_i^p \\& =\frac{\text { Rayonnement émis par la surface ( } i \text { ) et atteint la surface ( } j \text { ) }}{\text { Rayonnement émis par la surface (i) }}\end{aligned} \]
考察\(i\)正常发光时，\(j\)接受光的效果。
\[ F_{d A_j, d A_i}=\frac{\cos \theta_j \cos \theta_i d A_i}{\pi r^2} \]
\[ A_1 F_{1,2}=A_2 F_{2,1} \]
形状因子的叠加
\[ F_{1,2}=\sum_{j=1}^n F_{1,2 j} \quad F_{2,1} \neq \sum_{i=1}^n F_{2 i, 1} \]
\[ \begin{aligned}A_1 E_{b 1} F_{1,2} & =A_1 E_{b 1} F_{1,2 a}+A_1 E_{b 1} F_{1,2 b} \\F_{1,2} & =F_{1,2 a}+F_{1,2 b}\end{aligned} \]
\[ \begin{aligned}A_2 E_{b 2} F_{2,1} & =A_{2 a} E_{b 2} F_{2 a, 1}+A_{2 b} E_{b 2} F_{2 b, 1} \\A_2 F_{2,1} & =A_{2 a} F_{2 a, 1}+A_{2 b} F_{2 b, 1} \\F_{2,1} & =\frac{A_{2 a}}{A_2} F_{2 a, 1}+\frac{A_{2 b}}{A_2} F_{2 b, 1}\end{aligned} \]
解方程法求解形状因子
辐射度 Radiosité
辐射度是反射辐射和放射辐射之和。
\[ J_1=E_1+\rho_1 G_1=\varepsilon_1 E_{b 1}+(1-\alpha) G_1=\frac{E}{\alpha}-\frac{1-\alpha}{\alpha} \varphi^R=E_b-\left(\frac{1}{\varepsilon}-1\right) \varphi^R \]
从辐射度可以求两个物体之间的辐射：
\[ \Phi_{1,2}=A_1 J_1 F_{1,2}-A_2 J_2 F_{2,1} \]
\[ \Phi_{1,2}=\frac{A_1\left(E_{b 1}-E_{b 2}\right)}{\left(\frac{1}{\varepsilon_1}-1\right)+\frac{1}{F_{1,2}}+\frac{A_1}{A_2}\left(\frac{1}{\varepsilon_2}-1\right)}=\varepsilon_s A_1 F_{1,2}\left(E_{b 1}-E_{b 2}\right) \]
\(\varepsilon _s\)被称为系统放射率 Emissivité du système
\[ \varepsilon_s=\frac{1}{1+F_{1,2}\left(\frac{1}{\varepsilon_1}-1\right)+F_{2,1}\left(\frac{1}{\varepsilon_2}-1\right)} \]
与电路的类比
