量子简谐系统的波函数 Wavefunctions for the Harmonic Oscillator

量子谐振子的波函数

🐈‍⬛ 根据波函数的定义， \(\phi_n(x)\) 表示态 \(|n\rangle\) 在位置 \(x\)处的波函数值。因此， \(\phi_n(x)=\langle x \mid n\rangle\)，即态\(|n\rangle\) 在位置 \(x\) 处的波函数就是态 \(|n\rangle\) 和位置本征态 \(|x\rangle\)的内积。

基态波函数

首先考虑湮灭算子：

\[ \widehat{a}=\frac{\widetilde{x}+i \widetilde{p}}{\sqrt{2}}=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{x}+\hbar \sqrt{\frac{1}{m \hbar \omega}} \frac{\partial}{\partial x}\right) \]

\[ \widehat a\phi_0(x) = \widehat a \langle x|0\rangle = \langle x|\widehat{a}| 0\rangle = 0 \]

将湮灭算子带入得：

\[ \frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{x}+\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial x}\right) \phi_0(x)=0 \]

可以求出基态波函数：

\[ \phi_0(x)=A \exp \left(-\frac{m \omega x^2}{2 \hbar}\right) \]

通过波函数的归一性求解\(A\)：

\[ \int_{-\infty}^{+\infty} \phi_0^*(x) \phi_0(x) d x=1=A^2 \int_{-\infty}^{+\infty} \exp \left(-\frac{m \omega x^2}{\hbar}\right) d x=A^2 \sqrt{\frac{\pi \hbar}{m \omega}} \]

得：

\[ \phi_0(x)=\left(\frac{m \omega}{\pi \hbar}\right)^{1 / 4} \exp \left(-\frac{m \omega x^2}{2 \hbar}\right) \]

其概率密度为波函数的平方：

\[ \rho_0(x)=\left|\varphi_0(x)\right|^2=\sqrt{\frac{m \omega}{\pi \hbar}} \exp \left(-\frac{m \omega}{\hbar} x^2\right) \]

进一步求解其他能量本征态的波函数

应用创生算子：

\[ \widehat{a}^{\dagger} = \frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{x}-\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial x}\right) \]

得第一能量本征态波函数：

\[ \begin{aligned}\phi_1(x)&=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{x}-\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial x}\right) \phi_0(x)\\&=x \sqrt{\frac{2 m \omega}{\hbar}} \phi_0(x)\\&=\left[\left(\frac{m \omega}{\hbar}\right)^3 \frac{4}{\pi}\right]^{1 / 4} x \exp \left(-\frac{m \omega x^2}{2 \hbar}\right) \end{aligned} \]

或者可以直接写出第n阶能量本征态的波函数:

\[ \phi_n(x)=\sqrt{\frac{1}{n !}} \frac{1}{\sqrt{2^n}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{x}-\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial x}\right)^n \phi_0(x) \]

从波函数得到的一些结论

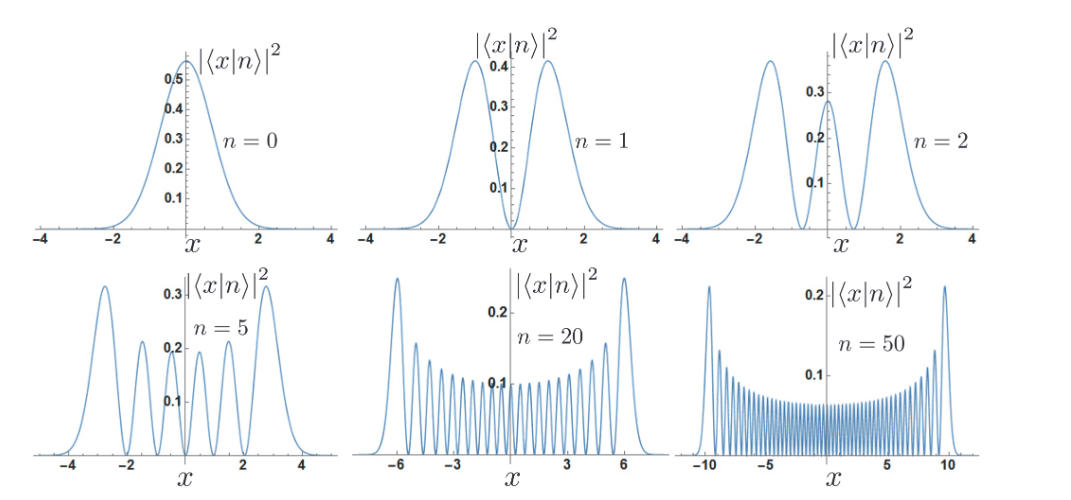
最低能量不为零的另一种解释

根据不确定性原理，基态的位移不能为零。位置概率密度有一个有限的扩展。由于波函数必须在大位移处消失，并且它必须在某处非零，因此必然存在曲率。因此，二阶导数不为零，因而平均动能不为零。

波函数的奇偶性

本征波函数是奇偶的。其奇偶性由\(𝑛\)给出。因此，概率密度始终是偶的。

Hermite多项式（Polynômes d’Hermite）

波函数可以用Hermite多项式表示：

\[ \phi_n(x)=\left(\frac{m \omega}{\pi \hbar}\right)^{1 / 4} \sqrt{\frac{1}{2^n n !}} \exp \left(-\frac{m \omega x^2}{2 \hbar}\right) H_n\left(\sqrt{\frac{m \omega}{\hbar}} x\right) \]

\[ \begin{array}{|c|c|}\hline n & H_n(x) \\\hline 0 & 1 \\1 & 2 x \\2 & 4 x^2-2 \\3 & 8 x^3-12 x \\4 & 16 x^4-48 x^2+12 \\5 & 32 x^5-160 x^3+120 x \\6 & 64 x^6-480 x^4+720 x^2-120 \\7 & 128 x^7-1344 x^5+3360 x^3-1680 x \\8 & 256 x^8-3584 x^6+13440 x^4-13440 x^2+1680 \\9 & 512 x^9-9216 x^7+48384 x^5-80640 x^3+30240 x \\10 & 1024 x^{10}-23040 x^8+161280 x^6-403200 x^4+302400 x^2-30240 \\\hline\end{array} \]

动能算符和位置算符的平均值

简谐系统的均值将非常容易计算。因为可以使用创生算子和湮灭算子表示波函数

\[ \widehat{x}=\sqrt{\frac{\hbar}{m \omega}} \frac{\widehat{a}+\widehat{a}^{\dagger}}{\sqrt{2}}, \quad \hat{p}=\sqrt{m \hbar \omega} \frac{\widehat{a}-\widehat{a}^{\dagger}}{i \sqrt{2}} \]

然后可以依次计算均值，以动量为例。根据本征态之间呈正交关系，动量的均值为\(0\)：

\[ \begin{aligned} \langle p\rangle_n & =\frac{\sqrt{m \hbar \omega}}{i \sqrt{2}}\left\langle n\left|\widehat{a}-\widehat{a}^{\dagger}\right| n\right\rangle \\ & =\frac{\sqrt{m \hbar \omega}}{i \sqrt{2}}(\sqrt{n}\langle n \mid n-1\rangle-\sqrt{n+1}\langle n \mid n+1\rangle)=0 \end{aligned} \]

考虑动量平方的均值，这将跟动能相关：

\[ \begin{aligned} \left\langle p^2\right\rangle_n & =\frac{-m \hbar \omega}{2}\left\langle n\left|\left(\widehat{a}-\widehat{a}^{\dagger}\right)^2\right| n\right\rangle \\ & =\frac{-m \hbar \omega}{2}\left(\langle n|\widehat{a} \widehat{a}| n\rangle+\left\langle n\left|\widehat{a}^{\dagger} \widehat{a}^{\dagger}\right| n\right\rangle-\left\langle n\left|\widehat{a}^{\dagger} \widehat{a}\right| n\right\rangle-\left\langle n\left|\widehat{a} \widehat{a}^{\dagger}\right| n\right\rangle\right)\\&=\frac{m \hbar \omega}{2}\left(\left\langle n\left|\widehat{a}^{\dagger} \widehat{a}\right| n\right\rangle+\left\langle n\left|\widehat{a}^{\dagger}\right| n\right\rangle\right)\\&=\frac{(2 n+1)}{2} m \hbar \omega \end{aligned} \]

在上述计算中，\(\langle n|\widehat{a} \widehat{a}| n\rangle\)和\(\left\langle n\left|\widehat{a}^{\dagger} \widehat{a}^{\dagger}\right| n\right\rangle\)返回分别将右矢转化为\(|n+2\rangle\)和\(|n-2\rangle\)，从而根据本征态的正交性将其消除。

最小波包

🐈‍⬛ 最小波包的定义通常是一个波函数在某个特定的态下，它在位置和动量空间中的不确定度取得最小值的状态。 🐈‍⬛ 对于谐振子基态\(|0⟩\)，位置和动量的不确定度的乘积被称为零点振动（zero-point oscillation）或零点波包（zero-point wavepacket）。对于谐振子，零点波包就是最小波包。

与上一节类似，分别考察位置算符和动量算符的基态方差。两种平方和均值的推导过程十分容易，且已经在上一节中展示，不再此赘述。

对于位置算符：

\[ \begin{aligned}\left\langle 0\left|\widehat{x}^2\right| 0\right\rangle & =\frac{\hbar}{2 m \omega}\left\langle 0\left|\widehat{a}^2+\widehat{a}^{\dagger 2}+2 \widehat{N}+1\right| 0\right\rangle=\frac{\hbar}{2 m \omega} \\\Delta_0 x & =\sqrt{\left\langle 0\left|\widehat{x}^2\right| 0\right\rangle-(\langle 0|\widehat{x}| 0\rangle)^2}=\sqrt{\frac{\hbar}{2 m \omega}}\end{aligned} \]

对于动能算符：

\[ \begin{aligned} \left\langle 0\left|\widehat{p}^2\right| 0\right\rangle & =-\frac{m \hbar \omega}{2}\left\langle 0\left|\widehat{a}^2+\widehat{a}^{\dagger 2}-2 \widehat{N}-1\right| 0\right\rangle=\frac{m \hbar \omega}{2} \\ \Delta_0 p & =\sqrt{\left\langle 0\left|\widehat{p}^2\right| 0\right\rangle-(\langle 0|\widehat{p}| 0\rangle)^2}=\sqrt{\frac{m \hbar \omega}{2}} \end{aligned} \]

从而得到最小波包：

\[ \Delta_0 x \Delta_0 p=\sqrt{\frac{\hbar}{2 m \omega}} \sqrt{\frac{m \hbar \omega}{2}}=\frac{\hbar}{2} \]

示例：三维简谐子

对于一个势能如下表示的简谐子，我们逐渐研究其性质：

\[ V(\vec{r})=\frac{1}{2} k r^2=\frac{1}{2} m \omega^2 r^2 \]

哈密顿算子和特征值

从哈密顿算子的一般形式出发：

\[ \widehat H = \frac{\widehat p}{2m}+\widehat{V} = \frac{\widehat p}{2m}+\frac{1}{2} m \omega^2 \widehat{r}^2 \]

根据薛定谔方程：

\[ \widehat H \psi = E\psi \]

在三维中展开：

\[ \left\{\begin{array}{l}\widehat{h}_x \phi_x(x)=\varepsilon_x \phi_x(x) \\\widehat{h}_y \phi_y(y)=\varepsilon_y \phi_y(y) \\\widehat{h}_z \phi_z(z)=\varepsilon_z \phi_z(z)\end{array}\right.\ avec \ \left\{\begin{array}{l} \widehat{h}_x=\frac{\widehat{p}_x^2}{2 m}+\frac{1}{2} m \omega^2 \widehat{x}^2 \\ \widehat{h}_y=\frac{\widehat{p}_y^2}{2 m}+\frac{1}{2} m \omega^2 \widehat{y}^2 \\ \widehat{h}_z=\frac{\widehat{p}_z^2}{2 m}+\frac{1}{2} m \omega^2 \widehat{z}^2 \end{array}\right. \]

由简谐子能量本征值公式：

\[ \varepsilon_n = (n+\frac 12 )\hbar\omega,\ n\in \mathbb N \]

得哈密顿算子得本征值：

\[ E_n = \varepsilon_{x,n}+\varepsilon_{y,n}+\varepsilon_{z,n} =\left(n_x+n_y+n_z+\frac{3}{2}\right) \hbar \omega,\left(n_x, n_y, n_z\right) \in \mathbb{N}^3 \]

由此，哈莫顿量的本征态必须由三个量子数来描述。式中，\(\left|n_i\right\rangle\)分别为\(n_i\)的本征态。

\[ \varphi(\vec{r})=\left\langle\vec{r} \mid n_x, n_y, n_z\right\rangle=\left\langle x \mid n_x\right\rangle\left\langle y \mid n_y\right\rangle\left\langle z \mid n_z\right\rangle \]

本征态描述

由于每个本征态都可以从基态应用创生算子得到，首先我们考虑基态\(\left|n_x = 0, n_y = 0, n_z = 0\right\rangle\)

根据创生算子的效果：

\[ \widehat{a}^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle \]

有对于单个维度：

\[ \left(\widehat{a}x^{\dagger}\right)^{n_x}|0,0,0\rangle=\sqrt{n_{x}!}\left|n_x, 0,0\right\rangle \]

同时有：

\[ \widehat{a}^{\dagger}=\frac{\tilde{x}-i \tilde{p}}{\sqrt{2}} = \widehat{a}_x^{\dagger}=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{x}-i \sqrt{\frac{1}{m \hbar \omega}} \widehat{p}_x\right)=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} x-\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial x}\right) \]

同理，对于其他维度：

\[ \left\{\begin{aligned} \widehat{a}_y^{\dagger} & =\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{y}-i \sqrt{\frac{1}{m \hbar \omega}} \widehat{p}_y\right) =\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} y-\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial y}\right)\\ \widehat{a}_z^{\dagger} & =\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} \widehat{z}-i \sqrt{\frac{1}{m \hbar \omega}} \widehat{p}_z\right)=\frac{1}{\sqrt{2}}\left(\sqrt{\frac{m \omega}{\hbar}} z-\sqrt{\frac{\hbar}{m \omega}} \frac{\partial}{\partial z}\right) \end{aligned}\right. \]

综上，得任何一个量子态与基态得关系：

\[ \left|n_x, n_y, n_z\right\rangle=\frac{1}{\sqrt{n_{x}!n_{y}!n_{z}!}}\left(\widehat{a}_x^{\dagger}\right)^{n_x}\left(\widehat{a}_y^{\dagger}\right)^{n_y}\left(\widehat{a}_z^{\dagger}\right)^{n_z}|0,0,0\rangle \]

能级的退化

相比于一维简谐子，三维简谐子的本征态与三个量子数相关，但当三个量子数的和相等时，能量相等。这意味着退化状态的发生。

对于能量\(E_n\)，讨论其中能量相等的本征态数量：

\[ g_{E_n} = \sum_{n_x = 0}^n(n-n_x+1) = \frac{((n+1)+1)(n+1)}{2} = \frac{(n+1)(n+2)}{2} \]

其中，\(n=\frac{E_n}{\hbar \omega}-\frac{3}{2}\)。简并性来自于系统的球对称性，或者说在起初的假设中，当三个量子数的和相等时，能量相等的性质即来自于球对称性。

计算位置平方的均值

使用创生算符和湮灭算符表示位置和动量，有：

\[ \widehat{r}=\sqrt{\frac{\hbar}{m \omega}} \frac{\widehat{a}+\widehat{a}^{\dagger}}{\sqrt{2}}, \quad \hat{p}=\sqrt{m \hbar \omega} \frac{\widehat{a}-\widehat{a}^{\dagger}}{i \sqrt{2}} \]

首先考虑一维情况。

\[ \begin{aligned}\widehat{x}^2&=\frac{\hbar}{2 m \omega}\left(\widehat{a}_x+\widehat{a}_x^{\dagger}\right)^2=\frac{\hbar}{2 m \omega}\left(\left(\widehat{a}_x\right)^2+\left(\widehat{a}_x^{\dagger}\right)^2+\widehat{a}_x \widehat{a}_x^{\dagger}+\widehat{a}_x^{\dagger} \widehat{a}_x\right)\\& = \frac{\hbar}{2 m \omega}\left(\left(\widehat{a}_x\right)^2+\left(\widehat{a}_x^{\dagger}\right)^2+2\widehat N_x+1\right)\end{aligned} \]

其均值：

\[ \langle \hat x^2 \rangle = \frac{\hbar}{2 m \omega}\left\langle n_x\left|\left(\widehat{a}_x\right)^2+\left(\widehat{a}_x^{\dagger}\right)^2+2 \widehat{N}_x+\widehat{\mathbb{1}}\right| n_x\right\rangle \]

对于湮灭算符或者创生算符，有：

\[ \begin{gathered}\left\langle n_x\left|\left(\widehat{a}_x\right)^2\right| n_x\right\rangle=\sqrt{n_x}\left\langle n_x\left|\widehat{a}_x\right| n_x-1\right\rangle=\sqrt{n_x\left(n_x-1\right)}\left\langle n_x \mid n_x-2\right\rangle=0 \\\left\langle n_x\left|\left(\widehat{a}_x^{\dagger}\right)^2\right| n_x\right\rangle=\sqrt{n_x+1}\left\langle n_x\left|\widehat{a}_x^{\dagger}\right| n_x+1\right\rangle=\sqrt{\left(n_x+1\right)\left(n_x+2\right)}\left\langle n_x \mid n_x+2\right\rangle=0\end{gathered} \]

因此，均值：

\[ \left\langle x^2\right\rangle=\frac{\hbar}{2 m \omega}\left\langle n_x\left|2 \widehat{N}_x+\widehat{\mathbb{1}}\right| n_x\right\rangle=\frac{\hbar}{2 m \omega}\left(2 n_x+1\right) \]

将三个维度的均值叠加：

\[ \left\langle r^2\right\rangle=\left\langle x^2\right\rangle+\left\langle y^2\right\rangle+\left\langle z^2\right\rangle =\frac{\hbar}{m \omega}\left(n_x+n_y+n_z+\frac{3}{2}\right) \]

计算动量平方的均值

根据一维的哈密顿算符：

\[ \widehat{h}_x=\frac{\widehat{p}_x^2}{2 m}+\frac{1}{2} m \omega^2 \widehat{x}^2 \]

有动量的均值：

\[ \left\langle p_x^2\right\rangle=2 m\left\langle h_x\right\rangle-m^2 \omega^2\left\langle x^2\right\rangle \]

其中，哈密顿算符的均值为：

\[ \left\langle h_x\right\rangle=\left\langle n_x\left|\widehat{h}_x\right| n_x\right\rangle=\left\langle n_x\left|\varepsilon_x\right| n_x\right\rangle=\varepsilon_x=\left(n_x+\frac{1}{2}\right) \hbar \omega \]

因此得到动量的均值为：

\[ \left\langle p_x^2\right\rangle=2\left(n_x+\frac{1}{2}\right) m \hbar \omega-m^2 \omega^2 \frac{\hbar}{2 m \omega}\left(2 n_x+1\right)=\left(n_x+\frac{1}{2}\right) m \hbar \omega \]

三维动量的均值：

\[ \left\langle p^2\right\rangle=\left(n_x+n_y+n_z+\frac{3}{2}\right) m \hbar \omega \]

最后从动量的均值得到动能的均值：

\[ \frac{1}{2 m}\left\langle p^2\right\rangle=\frac{1}{2}\left(n_x+n_y+n_z+\frac{3}{2}\right) \hbar \omega \]

可以发现正好为总能量的一半。

最小波包

对于简谐子，其动能和位移的均值都为零，因此有：

\[ \begin{aligned}&\Delta x=\sqrt{\left\langle x^2\right\rangle-\langle x\rangle^2}=\sqrt{\left\langle x^2\right\rangle}=\sqrt{\frac{\hbar}{2 m \omega}\left(2 n_x+1\right)}\\&\Delta p_x=\sqrt{\left\langle p_x^2\right\rangle-\left\langle p_x\right\rangle^2}=\sqrt{\left\langle p_x^2\right\rangle}=\sqrt{\left(n_x+\frac{1}{2}\right) m \hbar \omega}\end{aligned} \]

对应的三维空间的动能和位移：

\[ \begin{aligned}&\Delta r=\sqrt{\left\langle r^2\right\rangle-\langle r\rangle^2}=\sqrt{\left\langle r^2\right\rangle}=\sqrt{\frac{\hbar}{ m \omega}\left(n_x+n_y+n_z+3/2\right)}\\&\Delta p=\sqrt{\left\langle p^2\right\rangle-\left\langle p\right\rangle^2}=\sqrt{\left\langle p^2\right\rangle}=\sqrt{\left(n_x+n_y+n_z+3/2\right) m \hbar \omega}\end{aligned} \]

波包：

\[ \Delta r\Delta p = \hbar(n_x+n_y+n_z+3/2) \]

可见最小的标准偏差乘积来自于基态时的\(\frac{3\hbar}{2}\)，这是三个维度不确定度的叠加。

示例：可行的跃迁

电子在受到激发后，可能会从能级\(n\)跃迁到\(n^\prime\)。在这个过程中，如果跃迁的概率\(\left|\left\langle n|\widehat{x}| n^{\prime}\right\rangle\right|^2\)不为零，则认为跃迁是可以发生的。

使用湮灭算符和创生算符表示位移：

\[ \left|\left\langle n|\widehat{x}| n^{\prime}\right\rangle\right|^2=\frac{\hbar}{2 m \omega}\left|\left\langle n\left|\widehat{a}_x+\widehat{a}_x^{\dagger}\right| n^{\prime}\right\rangle\right|^2 = \frac{\hbar}{2 m \omega}\left(\sqrt{n^{\prime}} \delta_{n, n^{\prime}-1}+\sqrt{n^{\prime}+1} \delta_{n, n^{\prime}+1}\right)^2 \]

因此，电子只能跃迁到上下两个相近的轨道。