振动系统 Vibrating Systems
振动系统 Vibrating Systems
物理中的谐振振动
🐈⬛ 谐振振动是一类近似描述系统围绕平衡点运动的方法。
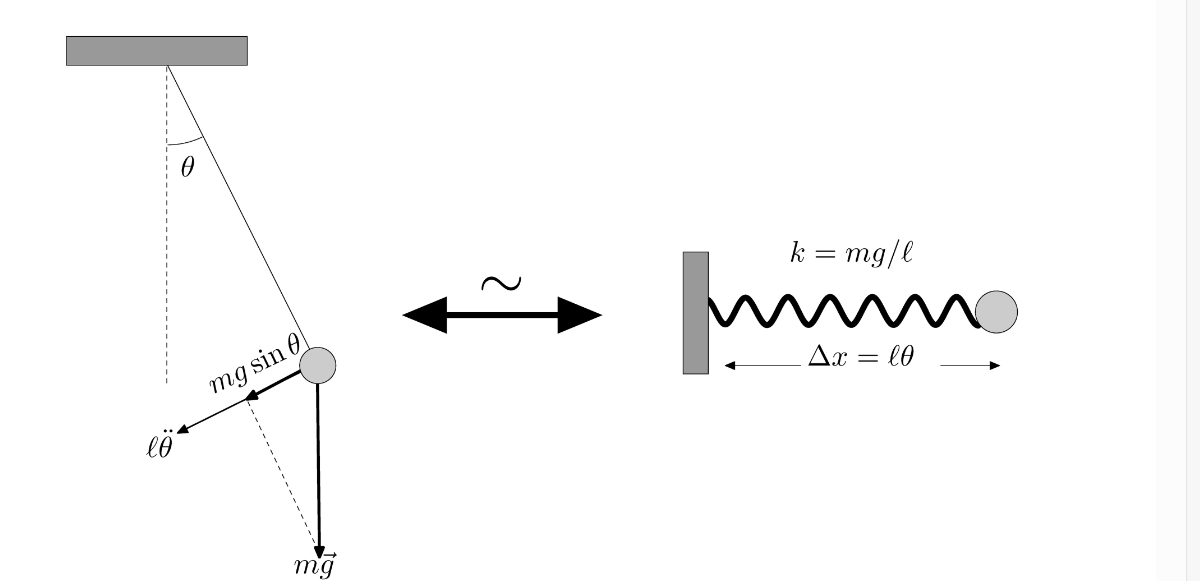
现实生活中的一些围绕平衡点的往复运动往往体现出与势能与位移呈二次关系。在这种情况下,可以将往复运动近似为简谐振动mouvement harmonique simple,将原本的运动系统近似为谐振子oscillateur harmonique。
一般的简谐振动的势能表达式为:
\[ V = V_0+\frac 12 m\omega^2\Delta x^2 = V_0+\frac 12 k \Delta x^2 \]
其中,\(\omega\)为谐振子的角频率;\(k\)是谐振子弹簧的弹性系数。
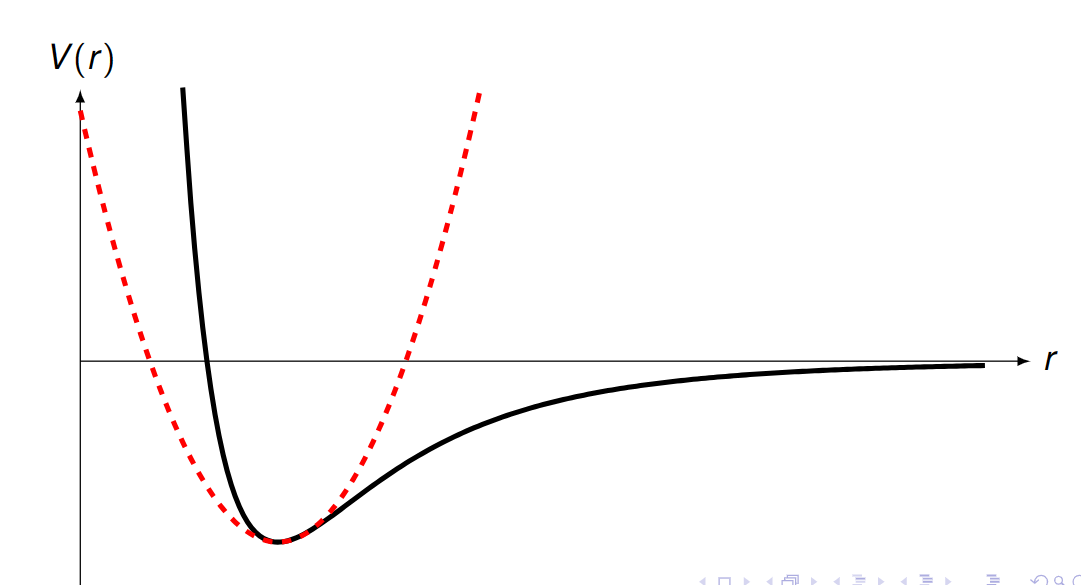
在量子力学中,将一些微观粒子的行为近似为简谐振动的尝试也是可行的。
假设粒子围绕平衡点\(x_0\)在一维振动振动,其势能可以被描述为:
\[ \begin{aligned}V(x)= & V\left(x_0\right)+\left(x-x_0\right)\left[\frac{\partial V(x)}{\partial x}\right]_{x_0} +\frac{1}{2}\left(x-x_0\right)^2\left[\frac{\partial^2 V(x)}{\partial x^2}\right]_{x_0}+\cdots\end{aligned} \]
在增加粒子位置与平衡位置始终有较小的偏差的假设后,有\(\frac{\partial V(x)}{\partial x}\sim 0\),剩余的部分则可近似为一个二次方程。
\[ \begin{aligned}V(x)= & V\left(x_0\right)+ +\frac{1}{2}\left(x-x_0\right)^2\left[\frac{\partial^2 V(x)}{\partial x^2}\right]_{x_0} \\=& V(x_0)+\frac 12 m \omega^2(x-x_0)^2 \end{aligned} \]
从而将其近似为一个\(\omega=\sqrt{\frac{1}{m}\left[\frac{\partial^2 V(x)}{\partial x^2}\right]_{x_0}}\)的简谐振动。
量子谐振子
量子力学中的谐振子
在经典物理的谐振子中,能量在全势能\((1 / 2) m \omega^2 \Delta x_{\max }^2\)和全动能\(p_{\max }^2 /(2 m)\)之间震荡。总能量可以写作:
\[ \varepsilon = \frac 12 m \omega^2 \Delta x^2+\frac 1{2m}p^2 \]
量子力学导致的问题出现在不确定原理给予了动量一个下界:
\[ \Delta x \Delta p \gtrsim \hbar / 2 \Rightarrow p \gtrsim p_{\min }=\frac{\hbar}{2 \Delta x} \]
这使得总能量总是存在一个下界:
\[ \varepsilon \gtrsim \varepsilon_{\min }=\frac{1}{2 m}\left(\frac{\hbar}{2 \Delta x}\right)^2+\frac{1}{2} m \omega^2 \Delta x^2 \]
对最小能量的表达式求导数可得在\(\Delta_x = \sqrt{\hbar / 2 m \omega}\) 是有最小值:
\[ \varepsilon \gtrsim \varepsilon_{\min }(\sqrt{\hbar / 2 m \omega} )=\frac{\hbar \omega}{2} \]
因此,在量子力学中,不存在零能量的粒子。
简谐哈密顿算子
🐈⬛ 狄拉克给出了一种应用量子力学形式主义的简谐运动求解方法。这种方法的优点是适用于物理学中的许多问题,例如辐射、晶体的振动模式以及一组相同粒子(如电子)的行为。
如前文所述,粒子的能量可以被假设为:
\[ E=\frac{p^2}{2 m}+\frac{1}{2} m \omega^2 x^2 \]
同时,哈密顿算子可以使用相关算子替换能量中所有的可观测量得到:
\[ \widehat{H}=\frac{\widehat p}{2 m} +\widehat{V}(\boldsymbol{r}) =\widehat{H}=\frac{\widehat{p}^2}{2 m}+\frac{1}{2} m \omega^2 \widehat{x}^2 \]
创生和湮灭算子
首先,定义一个无量纲的哈莫顿算子:
\[ \widetilde{H}=\frac{\widehat{H}}{\hbar \omega}=\frac{\widehat{p}^2}{2 m \hbar \omega}+\frac{1}{2} m \frac{\omega}{\hbar} \widehat{x}^2 \]
并依次定义无量纲的动能算子和位置算子:
\[ \widetilde{x}=\sqrt{\frac{m \omega}{\hbar}} \widehat{x} \quad \text {; } \quad \widetilde{p}=\sqrt{\frac{1}{m \hbar \omega}} \widehat{p} \]
由此,无量纲的哈密顿算子被定义为:
\[ \widetilde{H}=\frac{1}{2} \widetilde{p}^2+\frac{1}{2} \widetilde{x}^2 \]
考虑对无量纲的哈密顿算子进行分解,考虑\([\widetilde{x}, \widetilde{p}]=i \widehat{\mathbb{1}}\),有:
\[ \widetilde{H}=\frac{1}{2}(\widetilde{x}-i \widetilde{p})(\widetilde{x}+i \widetilde{p})+\frac{\widehat{\mathbb{1}}}{2} \]
注意,\(\frac{1}{2}(\widetilde{x}-i \widetilde{p})(\widetilde{x}+i \widetilde{p})=\frac{1}{2} \widetilde{p}^2+\frac{1}{2} \widetilde{x}^2+\frac{1}{2} i[\widetilde{x}, \widetilde{p}]\);因此增加恒等变换算符项\(\frac{\widehat{1}}{2}\)。
然后,定义两种非观测量的算子:创生算子和湮灭算子:
\[ \begin{aligned} \widehat{a} & =\frac{\widetilde{x}+i \widetilde{p}}{\sqrt{2}} ;\quad \widehat{a}^{\dagger} =\frac{\widetilde{x}-i \widetilde{p}}{\sqrt{2}} \end{aligned} \]
明显这两个算子不是厄米的,所以不是可观测量。可以一个相关的可观测量。
\[ \widehat{N}=\frac{1}{2}(\widetilde{x}-i \widetilde{p})(\widetilde{x}+i \widetilde{p})=\widehat{a}^{\dagger} \widehat{a} \]
无量纲哈密顿算子可以表示为:
\[ \begin{align}\widetilde{H}=\frac{1}{2}(\widetilde{x}-i \widetilde{p})(\widetilde{x}+i \widetilde{p})+\frac{\widehat{1}}{2}=\widehat{a}^{\dagger} \widehat{a}+\frac{\widehat{1}}{2} = \widehat{N}+\frac{\widehat{1}}{2}\end{align} \]
其中\(\widehat{N}\)是一个可观测量,为粒子数算符。
这些新定义的算子的对易子:
- \(\left[\widehat{a},
\widehat{a}^{\dagger}\right]=\frac{[i \widetilde{p},
\widetilde{x}]}{2}+\frac{[\widetilde{x},-i
\widetilde{p}]}{2}=\widehat{\mathbb{1}}\)
- \(\widehat{a}^{\dagger} \widehat{a} = \widehat N\),\(\widehat{a} \widehat{a}^{\dagger} = \widehat N + \widehat 1\)
- \([\widehat{N}, \widehat{a}]=\widehat{N} \widehat{a}-\widehat{a} \widehat{a}^{\dagger} \widehat{a}=\widehat{N} \widehat{a}-(\mathbb{1}+\widehat{N}) \widehat{a}=-\widehat{a}\)
- \([\widehat{N}, \widehat{a}^{\dagger}]=\widehat{a}^{\dagger}\)
量子谐振子的本征值 Eigenvalue
🐈⬛本征值(Eigenvalue):本征值是一个算符作用在其对应的本征态上所得到的数值结果
🐈⬛本征态(Eigenvector or eigenket):本征态是一个量子系统在某个物理量的测量下,对应于该物理量特定本征值的态。如果一个态是某个算符的本征态,那么当这个算符作用在这个态上时,结果将是这个态的一个倍数,这个倍数就是对应的本征值。
由\((1)\)式,可以导出哈密顿算符和\(\widehat N\)的关系:
\[ \widehat{H}=\left(\widehat{a}^{\dagger} \widehat{a}+\frac{1}{2}\right) \hbar \omega=\left(\widehat{N}+\frac{1}{2}\right) \hbar \omega \]
可见他们应该有相同的本征值,我们即为\(\nu\),即:
\[ \widehat{N}|\nu\rangle=\nu|\nu\rangle \]
这里,我们可以称\(\nu\)是量子系统的能量本征值,\(|\nu\rangle\)是量子系统的能量本征态。在之后的步骤中,我们会使用正整数\(n\)来代替\(\nu\),\(|n\rangle\)称为第\(n\)个能量本征态。
我们可以发现一些本征值具备的性质
本征值是非负实数
由于\(\widehat N\)是厄米型,其本征值都是实数。更进一步的,他们都是非负实数:
\[ \begin{aligned}\langle\nu|\widehat{N}| \nu\rangle =\langle\nu|\nu| \nu\rangle=\nu =\left\langle\nu\left|\widehat{a}^{\dagger} \widehat{a}\right| \nu\right\rangle=\| \widehat{a}|\nu\rangle \|^2 \geqslant 0\end{aligned} \]
本征值\(\nu\)为零当且仅当\(\widehat{a}|\nu\rangle = |\varnothing\rangle\)。
\(\widehat{a}|\nu\rangle , \widehat{a}^{\dagger}|\nu\rangle\)是\(\widehat N\)的本征态
\(\widehat{a}|\nu\rangle , \widehat{a}^{\dagger}|\nu\rangle\)是\(\widehat N\)的本征态,对应的本征值分别为\(\nu-1\)和\(\nu+1\)
\[ \begin{align}&\widehat{N}(\widehat{a}|\nu\rangle)=(\widehat{a} \widehat{N}-\widehat{a})|\nu\rangle=(\widehat{a} \nu-\widehat{a})|\nu\rangle=(\nu-1) \widehat{a}|\nu\rangle\\&\widehat{N}\left(\widehat{a}^{\dagger}|\nu\rangle\right)=\widehat{a}^{\dagger} \widehat{N}|\nu\rangle+\widehat{a}^{\dagger}|\nu\rangle=(\nu+1) \widehat{a}^{\dagger}|\nu\rangle\end{align} \]
\(\widehat{a}|\nu\rangle , \widehat{a}^{\dagger}|\nu\rangle\)的表述
湮灭算子和创生算子作用在\(\nu\)上的效果:
\[ \begin{align} &\widehat{a}^{\dagger}|\nu\rangle=\sqrt{\nu+1}|\nu+1\rangle \nonumber\\& \widehat{a}|\nu\rangle=\sqrt{\nu}|\nu-1\rangle \end{align} \]
根据\((4)\),可以解释两个算子名称的来源
🐈⬛创生算子 \(\widehat{a}^\dagger\):当创生算子 \(\widehat{a}^\dagger\) 作用于某个量子态 \(|\nu\rangle\) 时,它增加了一个粒子,并将系统从原本的状态 \(|\nu\rangle\) 转移到了一个粒子数增加的状态 \(|\nu+1\rangle\)。这个过程类似于在系统中“创造”了一个粒子,因此称为创生算子。
🐈⬛湮灭算子 \(\widehat{a}\):相反地,当湮灭算子 \(\widehat{a}\) 作用于某个量子态 \(|\nu\rangle\) 时,它减少了一个粒子,并将系统从原本的状态 \(|\nu\rangle\) 转移到了一个粒子数减少的状态 \(|\nu-1\rangle\)。这个过程类似于在系统中“消灭”了一个粒子,因此称为湮灭算子。
根据定义,\(|\nu\rangle\)是本征值\(\nu\)的本征态。根据\((2)\),\(\widehat{a}^{\dagger}|\nu\rangle\) 是对应于非简并本征值 \(\nu+1\) 的本征态。因此,它应该与本征值\(\nu+1\)的另一个本征态\(|\nu+1\rangle\)相关:
\[ \widehat{a}^{\dagger}|\nu\rangle \propto|\nu+1\rangle \]
然后根据\(|\nu\rangle\)是单位,可以求\(\widehat{a}^{\dagger}|\nu\rangle\)的范数来获得其准确表示:
\[ \| \widehat{a}^{\dagger}|\nu\rangle \|^2=\left\langle\nu\left|\widehat{a} \widehat{a}^{\dagger}\right| \nu\right\rangle=\langle\nu|\widehat{\mathbb{1}}+\widehat{N}| \nu\rangle=\nu+1 \]
同理:
\[ \| \widehat{a}|\nu\rangle \|^2=\left\langle\nu\left|\widehat{a}^{\dagger} \widehat{a}\right| \nu\right\rangle=\langle\nu|\widehat{N}| \nu\rangle=\nu \]
本征值是非负整数
本征值是非负整数。作为最终的符号,本征值\(n\in \mathbb{E}\)的本征态将被写为 \(|n\rangle\)。
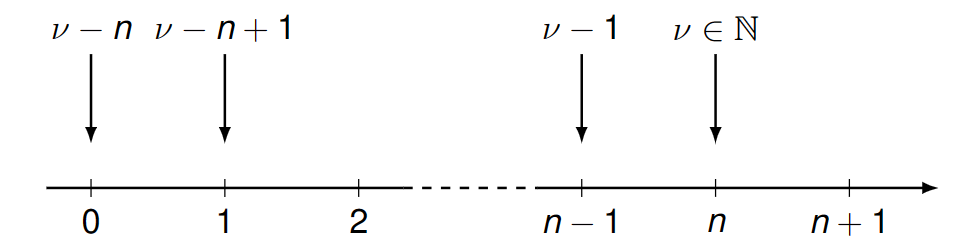
观察湮灭算符的边界,湮灭算符每次作用在某本征态\(|\nu\rangle\)上,会得到另一个本征态\(|\nu-1\rangle\),唯一的例外是\(|0\rangle\),湮灭算符作用在其上得到\(0\)而不是产生一个新的本征态。
因此,对于任何一个非零的本征态\(|\nu\rangle\),有其衍生:
\[ \{|\nu-k\rangle\ | \ k\in \mathbb{N},\nu-k^*\ne0,k^*<k,k^*\in \mathbb{N}\} \]
也是一个本征态。
而考虑第一条性质,本征值是非负实数。唯一满足这一条件的子集是为:
\[ \{|\nu-k\rangle\ | \ \nu\in\mathbb{N}, k\in \mathbb{N},\nu-k^*\ne0,k^*<k,k^*\in \mathbb{N}\} \]
可见本征值必须是非负整数。
简谐子的能量本征值
根据哈密顿算子:
\[ \widehat{H}=\left(\widehat{a}^{\dagger} \widehat{a}+\frac{1}{2}\right) \hbar \omega=\left(\widehat{N}+\frac{1}{2}\right) \hbar \omega \]
和薛定谔方程:
\[ \widehat H \psi = E\psi \]
可得谐振子能量的本征值可以表示为:
\[ \varepsilon_n=\left(n+\frac{1}{2}\right) \hbar \omega \quad \text { with } n \in \mathbb{N} \]
由此可见,最小能量为\(\varepsilon_0 = \frac{\hbar\omega}{2}\),与我们在本篇最初通过哈密顿原理计算得到的最小能量相同。最小能量不等于0,意味着量子简谐子永远不能静止。



