变分原理 Théorème variationnel
变分原理 Théorème variationnel
变分原理用于估计量子系统的基态能量以及与该能量相对应的波函数。该原理表述为:对于一个系统的基态波函数,若我们考虑一个任意的试探波函数,系统的基态能量将是所有试探波函数中能量最低的那个。换句话说,系统的基态能量是波函数的一个函数,而这个函数的值是通过最小化波函数的能量期望值来确定的。
问题描述
对于某一粒子,其薛定谔方程:
\[ \widehat{H}\left|\psi_i\right\rangle=\varepsilon_i\left|\psi_i\right\rangle \]
设置试探波函数,\(\left|\varphi_t\right\rangle=\sum_i c_i\left|\psi_i\right\rangle\)。如何选取试探波函数以获得基态能量。
变分原理
考虑试探波函数对应的能量均值:
\[ \begin{aligned} \langle E\rangle_t &=\langle H\rangle_t =\left\langle\varphi_t|\widehat{H}| \varphi_t\right\rangle =\sum_{i, j} c_i^* c_j\left\langle\psi_i|\widehat{H}| \psi_j\right\rangle =\sum_{i, j} c_i^* c_j\left\langle\psi_i\left|\varepsilon_j\right| \psi_j\right\rangle =\sum_{i, j} c_i^* c_j \varepsilon_j \delta_{i, j} \\ & =\sum_i\left|c_i\right|^2 \varepsilon_i\geqslant \varepsilon_0 \sum_i\left|c_i\right|^2=\varepsilon_0\left\langle\varphi_t \mid \varphi_t\right\rangle \end{aligned} \]
从而得到变分原理得数学表达:
\[ \frac{\left\langle\varphi_t|\widehat{H}| \varphi_t\right\rangle}{\left\langle\varphi_t \mid \varphi_t\right\rangle} \geqslant \varepsilon_0 \]
简单的例子
考虑试探函数:
\[ \varphi_t(x)=a_1 f_1(x)+a_2 f_2(x) \]
其中:
\[ f_1(x)=x^2-1 \quad f_2(x)=x^4-1 \]
求能量均值,假设\(x\in[-1,1]\):
\[ \begin{aligned}\langle H\rangle_t= & \left\langle\varphi_t|\widehat{H}| \varphi_t\right\rangle=\int_{-1}^1 \varphi_t^*(x)\left(-\frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2}\right) \varphi_t(x) \mathrm{d} x \\= & \int_{-1}^1\left(a_1 f_1(x)+a_2 f_2(x)\right) \times\left(-\frac{\hbar^2}{2 m} \frac{\partial^2}{\partial x^2}\right)\left(a_1 f_1(x)+a_2 f_2(x)\right) \mathrm{d} x\\=&\frac{\hbar^2}{2 m}\left(\frac{8}{3} a_1^2+\frac{32}{5} a_1 a_2+\frac{32}{7} a_2^2\right)\end{aligned} \]
考虑一个约束:
\[ \left\langle\varphi_t \mid \varphi_t\right\rangle=\int_{-1}^1 \varphi_t^*(x) \varphi_t(x) \mathrm{d} x=1\Leftrightarrow \frac{16}{15} a_1^2+\frac{256}{105} a_1 a_2+\frac{64}{45} a_2^2=1 \]
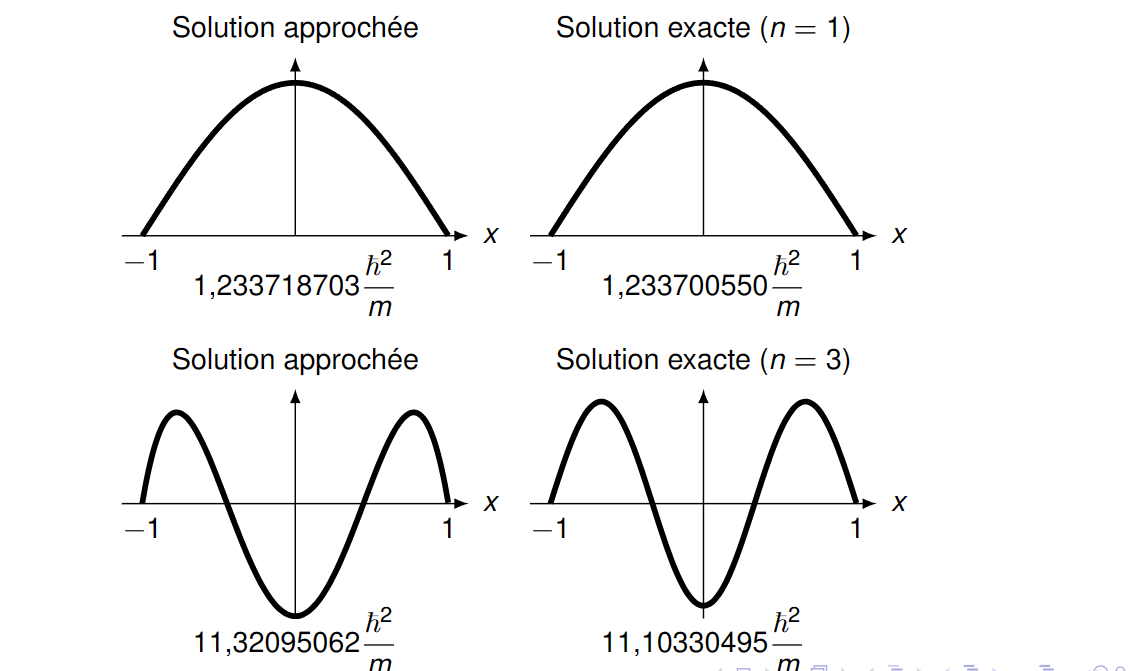
由此,即可求使得\(\langle H\rangle_t\)最小的\(a_1,a_2\)