氢:中心库伦势 Central Coulombic Potential
氢:中心库伦势 Central Coulombic Potential
双体问题,即一个原子核和一个电子,是唯一稳定且可解析解决的问题。术语“类氢hydrogenic”指的是该系统与氢原子的相似性。这种系统的总能量可以写作: \(E_{\text {经典 }}=\underbrace{\frac{p_Z^2}{2 M_Z}}_{\text {原子核动能 }}+\underbrace{\frac{p_e^2}{2 m_e}}_{\text {电子动能 }}-\underbrace{\frac{Z e^2}{4 \pi \epsilon_0\left|\boldsymbol{r}_e-\boldsymbol{R}_Z\right|}}_{\text {核-电子势能 }}\) \(*Z*\) 是原子核的电荷数
类氢系统的哈密顿量
使用相关算符替换每个可观测量:
\[ \widehat{H}=\frac{\hat{p}_Z^2}{2 M_Z}+\frac{\hat{p}_e^2}{2 m_e}-\frac{Z e^2}{4 \pi \epsilon_0\left|\widehat{\boldsymbol{r}}_e-\widehat{\boldsymbol{R}}_Z\right|} \]
使用质心参考系,有:
\[ \widehat{\boldsymbol{R}}=\left(m_e \widehat{\boldsymbol{r}}_e+M_Z \widehat{\boldsymbol{R}}_Z\right) /\left(m_e+M_Z\right),\ m=\left(m_e M_Z\right) /\left(m_e+M_Z\right) \]
从而使用相对坐标:
\[ \widehat{\boldsymbol r}=\widehat{\boldsymbol{r}}_e-\widehat{\boldsymbol{R}}_Z \]
哈密顿量被替换为:
\[ \widehat{H}=\frac{\widehat{P}^2}{2 M}+\frac{\widehat{p}^2}{2 m}-\frac{Z e^2}{4 \pi \epsilon_0 \widehat{r}} \]
其中,\(\text { } M=M_Z+m_e\),\(\widehat P\)是系统总体动量,与\(R\)相关,\(\widehat p\)是系统内部动量,与\(r\)相关。其中,前一项主要与原子核相关,后一项主要与电子相关。
解耦\(R\)和\(r\)得到,设\(\psi_{\text {tot }}(\boldsymbol{R}, \boldsymbol{r})=\psi_e(\boldsymbol{r}) \psi_\nu(\boldsymbol{R})\)是薛定谔方程的一个解,代入薛定谔方程,得到:
\[ \psi_e(\boldsymbol{r}) \frac{\widehat{P}^2}{2 M} \psi_\nu(\boldsymbol{R})+\psi_\nu(\boldsymbol{R}) \frac{\hat{p}^2}{2 m} \psi_e(\boldsymbol{r})-\psi_\nu(\boldsymbol{R}) \frac{Z e^2}{4 \pi \epsilon_0 \hat{r}} \psi_e(\boldsymbol{r})=\varepsilon_{\text {tot }} \psi_\nu(\boldsymbol{R}) \psi_e(\boldsymbol{r}) \]
其中 \(\varepsilon_{\text {tot }}\)是系统总能量。
系统总能量可以分为两个独立的部分,电子项和原子核项:\(\varepsilon_{\mathrm{tot}}=\varepsilon_\nu+\varepsilon_e\)
\[ \frac{1}{\psi_\nu(\boldsymbol{R})}\left(\frac{\widehat{P}^2}{2 M}-\varepsilon_\nu\right) \psi_\nu(\boldsymbol{R})+\frac{1}{\psi_e(\boldsymbol{r})}\left(\frac{\hat{p}^2}{2 m}-\frac{Z e^2}{4 \pi \epsilon_0 \hat{r}}-\varepsilon_e\right) \psi_e(\boldsymbol{r})=0 \]
双体问题被解耦,得到:
\[ \left\{\begin{align}{l}&\frac{\hat{P}^2}{2 M} \psi_\nu(\boldsymbol{R})=\varepsilon_\nu \psi_\nu(\boldsymbol{R}) \\&\frac{\hat{p}^2}{2 m} \psi_e(\boldsymbol{r})-\frac{Z e^2}{4 \pi \epsilon_0 \hat{r}} \psi_e(\boldsymbol{r})=\varepsilon_e \psi_e(\boldsymbol{r})\end{align}\right. \]
\((1)\)式对应一个自由原子核;\((2)\)式是电子的行为,可以观察到这是一个具备呈现球对称性的势能的例子,势能大小只跟距离的倒数有关。这个方程被称为中心场中的电子Électron dans un "champ central”。在球坐标系中考虑\((2)\):
\[ \frac{1}{2 m}\left(-\frac{\hbar^2}{r} \frac{\partial^2}{\partial r^2} r+\frac{\widehat{L}^2}{r^2}\right) \psi_e(\boldsymbol{r})-\frac{Z e^2}{4 \pi \epsilon_0 \hat{r}} \psi_e(\boldsymbol{r})=\varepsilon_e \psi_e(\boldsymbol{r}) \]
分解波函数为径向部分和球面谐函数的乘积:\(\psi_e(\boldsymbol{r})=R(r) Y_{\ell}^{m_{\ell}}(\theta, \varphi)\),角动量本征算符作用在其上得到\(\hbar^2 \ell(\ell+1)\),公式转化为:
\[ \left[\frac{\hbar^2}{2 m}\left(-\frac{1}{r} \frac{\partial^2}{\partial r^2} r+\frac{\ell(\ell+1)}{r^2}\right)-\frac{Z e^2}{4 \pi \epsilon_0 r}\right] R(r) Y_{\ell}^{m_{\ell}}(\theta, \varphi)=\varepsilon_e R(r) Y_{\ell}^{m_{\ell}}(\theta, \varphi) \]
约去角向部分,得到径向部分方程:
\[ -\frac{\hbar^2}{2 m} \frac{1}{r} \frac{\partial^2}{\partial r^2} r R(r)+V_{\ell}(r) R(r)=\varepsilon_e R(r) \ avec \ V_{\ell}(r)=-\frac{Z e^2}{4 \pi \epsilon_0 r}+\frac{\hbar^2 \ell(\ell+1)}{2 m r^2} \]
其中,\(V_l\)被称为有效势能,第一项表示电子吸引attraction électrostatique,第二项表示离心排斥répulsion centrifuge。
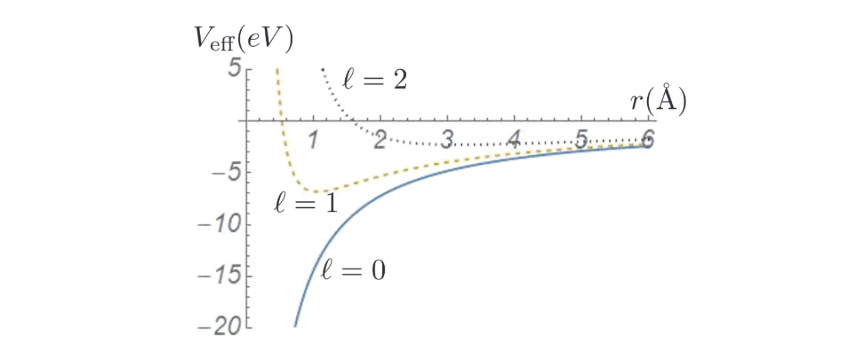
考虑\(rR\)一项,\(\int_{\Delta r} \int_{\Delta \Omega}\left|R(r) Y_{\ell}^{m_{\ell}}(\theta, \varphi)\right|^2 r^2 d r \sin \theta d \theta d \varphi\)是在体积元\(r^2 \Delta r \Delta \Omega\)中电子的概率,因此 \(r^2|R(r)|^2\)就是径向概率密度。可以设\(P = rR\),得到:
\[ -\frac{\hbar^2}{2 m } \frac{\partial^2}{\partial r^2} P(r)+V_{\ell}(r) P(r)=\varepsilon_e P(r) \]
类氢原子的态矢量\(\left|n, \ell, m_{\ell}, \pm 1 / 2\right\rangle\),波函数\(\phi_{n \ell m_{\ell}}(\boldsymbol{r})=R_{n \ell}(r) Y_{\ell}^{m_{\ell}}(\theta, \varphi)\)
当\(l = 0\)时,电子吸引占主导,径向方程:
\[ -\frac{\hbar^2}{2 m } \frac{\partial^2}{\partial r^2} P_{n 0}(r)-\frac{Z e^2}{4 \pi \epsilon_0 r} P_{n 0}(r)=0 \]
当\(l\ne 0\)时,离心排斥占主导:
\[ -\frac{\hbar^2}{2 m} \frac{\partial^2}{\partial r^2} P_{n \ell}(r)+\frac{\hbar^2 \ell(\ell+1)}{2 m r^2} P_{n \ell}(r)=0 \]
径向部分具备一个封闭形式:
\[ R_{n \ell}(r)=-\sqrt{\left(\frac{2 Z}{n a_0}\right)^3 \frac{(n-\ell-1)!}{2 n[(n+\ell)!]}} e^{-Z r /\left(n a_0\right)}\left(\frac{2 Z}{n a_0} r\right)^{\ell} L_{n+\ell}^{2 \ell+1}\left(\frac{2 Z}{n a_0} r\right) \]
- \(L_{n+\ell}^{2 \ell+1}\)是勒让德多项式。
氢原子能量和波函数
根据径向方程:
\[ \frac{\partial^2}{\partial r^2} P(r)+\frac{2 m}{\hbar^2} \frac{Z e^2}{4 \pi \epsilon_0 r} P(r)-\frac{\ell(\ell+1)}{r^2} P(r)=-\frac{2 m}{\hbar^2} \varepsilon_e P(r) \]
代入\(R_{nl}\)的表达式,可得:
\[ \varepsilon_e=-\frac{e^2}{4 \pi \epsilon_0 a_0} \frac{Z^2}{2 n^2}=-\frac{1}{2} m c^2\left(\frac{Z \alpha}{n}\right)^2 \quad \text { with } n \in \mathbb{N}^* \]
其中,\(\alpha\)是精细结构常数,\(\alpha=\frac{e^2}{4 \pi \epsilon_0 \hbar c} \approx \frac{1}{137}\)。在一些其他的能量表达方式中,能量被表述为:
\[ \varepsilon_{\boldsymbol{e}}=-\frac{m}{\hbar^2}\left(\frac{Z e^2}{4 \pi \epsilon_0}\right)^2 \frac{1}{2 n^2}=-\frac{1}{2 m} \frac{\hbar^2}{a_0^2} \frac{Z^2}{n^2} \]
其中,\(a_0\)被称为玻尔半径,有\(a_0 \triangleq \frac{4 \pi \epsilon_0 \hbar^2}{m e^2} \approx 0,529 \AA\)。无论如何,合并所有参数,有:
\[ \varepsilon_n=-\frac{1}{2 m} \frac{\hbar^2}{a_0^2} \frac{Z^2}{n^2}=-Z^2 \frac{13,6}{n^2} \mathrm{eV} \]
有趣的是,这种能量似乎不取决于角动量,这意味着它是兼并的。综合考虑角量子数,磁量子数,自旋量子数,兼并度为:\(g_n=2 \sum_{\ell=0}^{n-1}(2 \ell+1)=2 n^2\)。
另一方面,节点数似乎与\(n\)有关。具体来说,径向部分有\(n-1\)个节点。
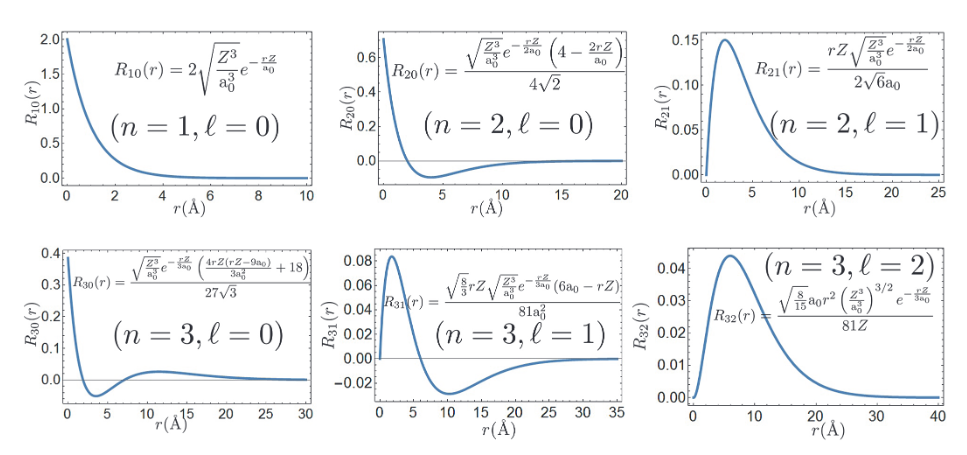
节点越多,振荡次数越多。动能由 \(-\hbar^2 /(2 m) \int \phi^*(x) \frac{\partial^2}{\partial x^2} \phi(x) d x\)会给出,通过部分积分 (考虑到在无穷远处的必要抵消)得到\(\hbar^2 /(2 m) \int\left|\frac{\partial}{\partial x} \phi(x)\right|^2 d x\)。这个积分与波函数的平均二次变化成正比。如果振荡很多次,平均值会很大,动能也会很大。
因为能量仅在 \(n \rightarrow \infty\) 时达到零。这是由于库仑吸引势的缓慢衰减
精细结构常数 \(\alpha\) 大约是 \(1 / 137\) 。因此,电子能量在核电荷 \(Z=50\) 左右的范围内接近其静止质量 \(m c^2 \approx 512 \mathrm{keV}\) 。在这个范围内,需要考虑相对论效应。
在氢原子情况 \((Z=1)\) 中,基态 \((n=1)\) 对应于 \(-13.6 \mathrm{eV}\) 的能量。因此, \(13.6 \mathrm{eV}\)是将电子从原子核分离所需的最小能量,即“电离能”。
激发电子的能量有Balmer和Ritz提出的公式计算:
\[ \hbar \omega=\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right) \times 13.6 \mathrm{eV} \]
其中 \(n_i\) 和 \(n_f\) 分别是初始和最终态的主量子数。
最后简单讨论\(p\)轨道的形状。
使用\(r=\left|y_{\ell, m_{\ell}}(\theta, \varphi)\right|\)表示\(p\)轨道。先考虑其中一个,有\(r=\left|y_{1,0}(\theta, \varphi)\right|=\left|Y_1^0(\theta, \varphi)\right|=\sqrt{\frac{3}{4 \pi}}|\cos \theta|\),从而有:
\[ r=\sqrt{\frac{3}{4 \pi}} \frac{|z|}{r} \Leftrightarrow r^2=x^2+y^2+z^2=\sqrt{\frac{3}{4 \pi}}|z|= \pm \sqrt{\frac{3}{4 \pi}} z \Leftrightarrow x^2+y^2+\left(z \pm \sqrt{\frac{3}{16 \pi}}\right)^2=\frac{3}{16 \pi} \]
从而可见\(p\)轨道是两个以\(z = \pm \sqrt{\frac{3}{16 \pi}}\)为球心,\(r = \sqrt{\frac{3}{16 \pi}}\)的球组成的。
其他的也类似。



