自旋:另一个自由度 Spin, a New Degree of Freedom
自旋:另一个自由度 Spin, a New Degree of Freedom
施特恩-格拉赫实验
电子的磁矩
原子中的电子由 \(\widehat{L}_z\) 和 \(\widehat{L}^2\) 共享的本征态描述。与带电粒子相关联的角动量的存在将产生磁矩。对于角动量为\(L\)的电子,其形成的磁矩:
\[ \boldsymbol{\mu}=\frac{-e}{2} \boldsymbol{r} \wedge \boldsymbol{v}=\gamma \boldsymbol{L} \]
其中 \(\gamma=-\frac{e}{2 m}\) 被称为“旋磁比rapport gyromagnétique”。由于量子角动量只能以\(\hbar\)的整数倍变化,因此磁矩也是量子化的。其单位为:\(\mu_B=\frac{e \hbar}{2 m}\),被称为玻尔兹曼磁矩。
与可变磁场的相互作用
当携带磁矩的原子穿过一个沿\(e_z\)方向均与的磁场时,其受力与磁场梯度\(\vec{\nabla} \boldsymbol{B}=\partial B / \partial z \boldsymbol{e}_z\)相关:
\[ F_z=\mu_z \frac{\partial B}{\partial z}=\gamma L_z \frac{\partial B}{\partial z} \]
施特恩-格拉赫实验
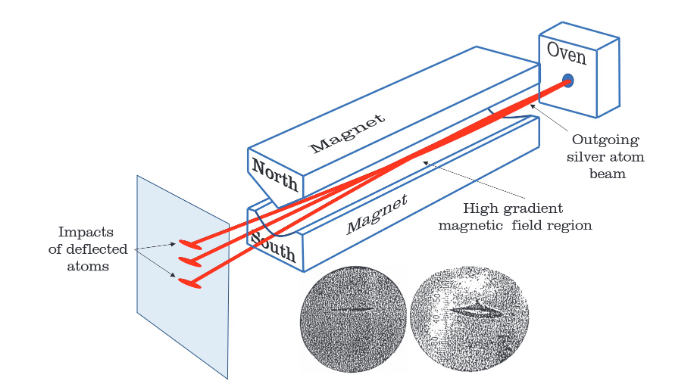
施特恩-格拉赫实验通过高温炉射出银原子,准直后形成原子射线束,通过不均匀磁场区域,射线束发生偏折后落在屏上。
这个实验有两个结果:
- 角动量未量子化,Larmor经典模型适用。穿过梯度场区域的原子根据其磁矩的随机分布而偏转,它们对检测屏的影响将形成一个独特的、均匀的和延长的标记。
- 角动量的量子化存在,黑斑的数量必须对应于\(z\)方向角动量的可能分量数\(2 \ell+1\)个。
然而,最终实验仅观察到两个斑点。这意味着角量子数\(l = \frac 12\)。
对实验的解释:自选
回忆\(l\)的取值的确认。起初,我们认为\(-n / 2 \leqslant \mu \leqslant n / 2\),因此\(\mu\)存在取\(1/2\)的可能。而后,我们根据\(2\pi\)对称性认为\(l\)为整数。如果实验结果正确,意味着电子并不具备\(2\pi\)对称性,而是具备\(4\pi\)对称性。或许,存在另一类型的角动量,其投影可以取的半整数因子的值。我们将其称为自选角动量\(S\),属于电子。其存在可以在设置\(l = m_l = 0\)的实验中证明。
另一个更为精确的实验,发现原子的偏转程度是自旋角动量应有的两倍。
\[ \boldsymbol{\mu}=-\frac{e}{2 m_e} g \boldsymbol{S}=-\frac{\mu_B}{\hbar} g \boldsymbol{S}=\gamma g \boldsymbol{S} \]
其中\(g\)被称为\(g\)因子或者兰蒂因子。对于电子,\(g = 2\),即为实验中发现的片场程度为理想的两倍的情况。
半整数自旋的粒子被称为费米子(如电子),整数的则称为玻色子(如光子)
泡利矩阵 Matrices de Pauli
自旋本征态
如上实验所述,自旋角动量\(z\)轴上的投影仅可能为\(1/2\)或\(-1/2\)。这两种状态通常使用本征态符号\(\mid\uparrow\rangle\)和\(\mid\downarrow\rangle\)来表示,记为自旋向上spin up和自旋向下spin down。
\[ \widehat{S}_z\mid\uparrow\rangle=\frac{\hbar}{2}\mid\uparrow\rangle \quad \text { and } \quad \widehat{S}_z\mid\downarrow\rangle=-\frac{\hbar}{2}\mid\downarrow\rangle \]
有趣的是,电子或任何量子粒子的自旋态没有位置表示。因此,它必须被视为额外的自由度。
泡利矩阵
自旋态可以用矩阵表示,称为泡利矩阵。这是在\(\{\mid\uparrow\rangle,\mid\downarrow\rangle\}\)基下的矩阵表示。因此:
\[ \widehat{S}_z=\frac{\hbar}{2} \widehat{\sigma}_z \quad \text { with } \quad \widehat{\sigma}_z=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) \]
此时,\((1,0)\)表示\(\mid\uparrow\rangle\),\((0,1)\)表示\(\mid\downarrow\rangle\)。
考虑阶梯算子,由于自旋仅有两个取值,有:
\[ \begin{array}{lll}\widehat{S}_{+}\mid\uparrow\rangle=0 & \text { and } & \widehat{S}_{+}\mid\downarrow\rangle=\hbar\mid\uparrow\rangle \\\widehat{S}_{-}\mid\downarrow\rangle=0 & \text { and } & \widehat{S}_{-}\mid\uparrow\rangle=\hbar\mid\downarrow\rangle\end{array} \]
由此可以得到阶梯算子的泡利矩阵:
\[ \widehat{S}_{+}=\hbar\left(\begin{array}{ll}0 & 1 \\0 & 0\end{array}\right) \quad \text { and } \quad \widehat{S}_{-}=\hbar\left(\begin{array}{ll}0 & 0 \\1 & 0\end{array}\right) \]
由此,可以计算\(x\)方向和\(y\)方向的算子:
\[ \widehat{S}_x=\frac{\widehat{S}_{+}+\widehat{S}_{-}}{2}=\frac{\hbar}{2}\left(\begin{array}{ll}0 & 1 \\1 & 0\end{array}\right) \quad \text { and } \quad \widehat{S}_y=\frac{\widehat{S}_{+}-\widehat{S}_{-}}{2 i}=\frac{\hbar}{2}\left(\begin{array}{cc}0 & -i \\i & 0\end{array}\right) \]
综上,三个方向的泡利矩阵:
\[ \widehat{\sigma}_x=\left(\begin{array}{ll}0 & 1 \\1 & 0\end{array}\right) \quad \widehat{\sigma}_y=\left(\begin{array}{cc}0 & -i \\i & 0\end{array}\right) \quad \widehat{\sigma}_z=\left(\begin{array}{cc}1 & 0 \\0 & -1\end{array}\right) \]
泡利不相容原理
多电子波函数
多电子的波函数可以被写作\(\psi\left(\vec{x}_1, \ldots, \vec{x}_i, \ldots, \vec{x}_j, \ldots, \vec{x}_N\right)\)。它们都是相同的,所以将粒子作为一对的任何交换都必须使系统保持不变。
\[ \left|\psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_j, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_N\right)\right|^2=\left|\psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_j, \ldots, \boldsymbol{x}_N\right)\right|^2 \]
因此,两个波函数仅在相位上允许差异:
\[ \begin{aligned}&\psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_j, \ldots, \boldsymbol{x}_N\right)=e^{i \varphi} \psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_j, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_N\right)\\&\psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_j, \ldots, \boldsymbol{x}_N\right)=e^{2 i \varphi} \psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_j, \ldots, \boldsymbol{x}_N\right)\end{aligned} \]
同理再次交换之后,可以发现\(e^{i\phi}\)只能取\(1\)或者\(-1\)。
如果波函数对于两个粒子的任何排列都是不变的。波函数被称为“完全对称 totalement symétrique”,对应的粒子称为玻色子 bosons,它们具备整数自旋spin entier。
如果相位因子为-1,波函数被称为“完全反对称 totalement antisymétrique”。它们具备具有半整数自旋spin demi-entier,被称为费米子 fermions。
泡利原理 Principe d’exclusion de Pauli
由 N 个不可区分的费米子组成的系统的波函数是完全反对称的。或者说:具有相同自旋状态且在空间中相同位置的两个相同费米子的概率密度为零。
证明十分简单:
\[ \begin{aligned}& \psi\left(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_i, \ldots, \boldsymbol{x}_N\right) \\& \quad=-\psi(\boldsymbol{x}_1, \boldsymbol{x}_2, \ldots, \underbrace{\boldsymbol{x}_i, \ldots, \boldsymbol{x}_i}_{\text {permutation! }}, \ldots, \boldsymbol{x}_N)=0\end{aligned} \]
例子:核磁共振
核磁共振



