旋转系统 Rotating Systems
旋转系统 Rotating Systems
刚体的能量通常由两部分描述:平移动能\(\frac{\boldsymbol{p}^2}{2 m}\)和旋转动能\(\frac{\boldsymbol{L}^2}{2 I}\),其中\(p\)被称为动量,而\(L\)被称为角动量。本章讨论量子力学体系中的角动量。
角动量算子
角动量算子的定义
角动量使用相对旋转轴的位置和动量之间的叉乘定义:
\[ \boldsymbol{L}=\boldsymbol{r} \times \boldsymbol{p} \]
因此,可以使用位置算子和动量算子来定义角动量算子:
\[ \begin{aligned}& \widehat{L}_x=\widehat{y} \widehat{p}_z-\widehat{z} \widehat{p}_y=-i \hbar\left(y \frac{\partial}{\partial z}-z \frac{\partial}{\partial y}\right) \\& \widehat{L}_y=z \widehat{p}_x-\widehat{x} \widehat{p}_z=-i \hbar\left(z \frac{\partial}{\partial x}-x \frac{\partial}{\partial z}\right) \\& \widehat{L}_z=\widehat{x} \widehat{p}_y-\widehat{y} \widehat{p}_x=-i \hbar\left(x \frac{\partial}{\partial y}-y \frac{\partial}{\partial x}\right)\end{aligned} \]
对位置向量和动量向量的空间反演\((\theta \rightarrow \pi-\theta ; \varphi \rightarrow \varphi+\pi)\)不会改变角动量算子。因此,对于任何反演算子\(\widehat{\Pi} f(\theta, \varphi)=f(\pi-\theta, \varphi+\pi)\),有:
\[ [\widehat{\Pi}, \widehat{\boldsymbol{L}}]=0 \]
角动量的对易性
由于位置算子和动量算子不是对易的,不同方向的角动量算子之间也不会是对易的:
\[ \left[\widehat{L}_x, \widehat{L}_y\right]=-i\hbar\left[\widehat{y} \hat{p}_z-\widehat{z} \hat{p}_y, z \hat{p}_x-\widehat{x} \hat{p}_z\right] \]
展开对易子:
\[ \begin{aligned}{\left[\widehat{L}_x, \widehat{L}_y\right] } & =\left(\widehat{y} \widehat{p}_z-\widehat{z} \widehat{p}_y\right)\left(\widehat{z} \widehat{p}_x-\widehat{x} \widehat{p}_z\right)-\left(\widehat{z} \widehat{p}_x-\widehat{x} \widehat{p}_z\right)\left(\widehat{y} \widehat{p}_z-\widehat{z} \widehat{p}_y\right) \\& =\widehat{z} \widehat{x} \widehat{p}_y \widehat{p}_z-\widehat{x} \widehat{p}_z \widehat{z} \widehat{p}_y+\widehat{y} \widehat{p}_z \widehat{z} \widehat{p}_x-\widehat{z} \widehat{y} \widehat{p}_x \widehat{p}_z \\& =i \hbar\left(\widehat{x} \widehat{p}_y-\widehat{y} \widehat{p}_x\right)=i \hbar \widehat{L}_z\end{aligned} \]
同时有:
\[ \left[\widehat{L}_y, \widehat{L}_z\right]=i \hbar \widehat{L}_x \quad \text { and } \quad\left[\widehat{L}_z, \widehat{L}_x\right]=i \hbar \widehat{L}_y \]
根据广义海森堡不确定性原理,有:
\[ \Delta_\psi\left(L_x\right) \Delta_\psi\left(L_y\right) \geqslant \frac{\hbar}{2}\left\langle L_z\right\rangle_\psi \]
因此,不同方向的角动量不能被同时精确测量。
考虑角动量的平方模量与某一方向角动量的对易子:
\[ \begin{aligned} {\left[\widehat{L}^2, \widehat{L}_z\right] } & =\left[\widehat{L}_x^2, \widehat{L}_z\right]+\left[\widehat{L}_y^2, \widehat{L}_z\right]+\left[\widehat{L}_z^2, \widehat{L}_z\right] \\ & =\widehat{L}_x\left[\widehat{L}_x, \widehat{L}_z\right]+\left[\widehat{L}_x, \widehat{L}_z\right] \widehat{L}_x+\widehat{L}_y\left[\widehat{L}_y, \widehat{L}_z\right]+\left[\widehat{L}_y, \widehat{L}_z\right] \widehat{L}_y \\ & =-i \hbar \widehat{L}_x \widehat{L}_y-i \hbar \widehat{L}_y \widehat{L}_x+i \hbar \widehat{L}_y \widehat{L}_x+i \hbar \widehat{L}_x \widehat{L}_y=0 \end{aligned} \]
同时有:
\[ \left[\widehat{L}^2, \widehat{L}_x\right]=0 \quad \text { and } \quad\left[\widehat{L}^2, \widehat{L}_y\right]=0 \]
可见,尽管不能同时知道角动量分量,但单个分量与平方模量兼容。因此,关于角动量可获得的知识至多是在一个特定轴及其范数上的投影。
角动量的本征值和本征态
研究纯旋转体的角动量问题,纯旋转体的动能只有角动量动能,没有平动动能。
由于不同方向的角动量分量之间不对易,寻找角动量的共同本征态是有意义的。纯旋转问题的CSCO(可交换观测量的完全集合)是角动量平方算子\(\widehat{L}^2\)和某一方向角动量算子\(\widehat{L}_z\)的共同本征态:\(\left\{\widehat{L}^2, \widehat{L}_z\right\}\)。这两个特征值具备的信息可以被认为完全确认旋转体的状态。
假设 \(\widehat{L}^2, \widehat{L}_z\) 两者的本征值分别为:\(\lambda^2, \mu\),对应的本征态为\(\left| \lambda, \mu \right\rangle\),则有:
\[ \widehat{L}^2\left|\lambda^2, \mu\right\rangle=\lambda^2 \hbar^2\left|\lambda^2, \mu\right\rangle \quad \text { and } \quad \widehat{L}_z\left|\lambda^2, \mu\right\rangle=\mu \hbar\left|\lambda^2, \mu\right\rangle \]
值得一提的是,假设 \(\left|\lambda^2, \mu\right\rangle\) 是CSCO基于仅了解 \(\widehat{L}^2, \widehat{L}_z\) 就足以确定量子的状态,但这是未必的。目前,我们假设 \(\left\{\widehat{L}^2, \widehat{L}_z\right\}\) 是合法的 CSCO,并且将本征态写为:\(\left| \lambda, \mu \right\rangle\) 就足够了。
本征值的性质
角动量平方算符始终大于 \(Z\) 分量的平方算符:\(\lambda^2 \geqslant \mu^2\)。这很好理解,因为角动量平方算符包含了所有方向的角动量,而 \(Z\) 分量的平方算符只包含了一个方向的角动量。可以通过下式定量证明:
\[ \lambda^2 \hbar^2-\mu^2 \hbar^2 = \left\langle\lambda^2, \mu\left|\widehat{L}^2-\widehat{L}_z^2\right| \lambda^2, \mu\right\rangle=\left\langle\lambda^2, \mu\left|\widehat{L}_x^2+\widehat{L}_y^2\right| \lambda^2, \mu\right\rangle \geqslant 0 \]
\(\widehat{L}^2-\widehat{L}z^2\)可以被写作两个新的互为伴随的角动量算子的均值。
\[ \widehat{L}^2-\widehat{L}z^2=\widehat{L}x^2+\widehat{L}y^2=\frac{1}{2}\left(\widehat{L}{+} \widehat{L}{-}+\widehat{L}{-} \widehat{L}{+}\right)\quad with \quad \widehat{L}_{+}=\widehat{L}_x+i \widehat{L}y ,\ \ \widehat{L}{-}=\widehat{L}_x-i \widehat{L}_y \]
由于\(\widehat L_x\)和\(\widehat L_y\)是厄米的,因此\(\widehat L_+\)和\(\widehat L_-\)不可能是厄米的。因此,这两个算符不可能与可观测量相关联。
新定义的两个算子被称为阶梯算子opérateurs d’échelle,其中\(\widehat L_+\)被称为升算子,\(\widehat L_-\)被称为降算子。它们在角动量中的作用类似于创生/湮灭算子在震动问题中的作用。
\[ \widehat{L}_{+}\left|\lambda^2, \mu\right\rangle=c_{+}\left|\lambda^2, \mu+1\right\rangle \quad \text { and } \quad \widehat{L}_{-}\left|\lambda^2, \mu\right\rangle=c_{-}\left|\lambda^2, \mu-1\right\rangle \]
注意,阶梯算符改变\(z\)方向角动量算子的本征值而不是角动量平方算子的本征值。
其中,\(c_+\)和\(c_-\)由正则化条件求得。
它们与原本的两个算符的对易子:
- \(\widehat{L}_{+}\left|\lambda^2, \mu\right\rangle=c_{+}\left|\lambda^2, \mu+1\right\rangle \quad \text { and } \quad \widehat{L}_{-}\left|\lambda^2, \mu\right\rangle=c_{-}\left|\lambda^2, \mu-1\right\rangle\)
- \(\left[\widehat{L}^2, \widehat{L}_{ \pm}\right]=0\)
根据阶梯算符与\(z\)方向角动量算子的对易子,可以发现\(\widehat{L}_{ \pm}\left|\lambda^2, \mu\right\rangle\)是角动量算子的特征向量:
\[ \widehat{L}_z \widehat{L}_{ \pm}\left|\lambda^2, \mu\right\rangle=\left( \pm \hbar \widehat{L}_{ \pm}+\widehat{L}_{ \pm} \widehat{L}_z\right)\left|\lambda^2, \mu\right\rangle=( \pm 1+\mu) \hbar \widehat{L}_{ \pm}\left|\lambda^2, \mu\right\rangle \]
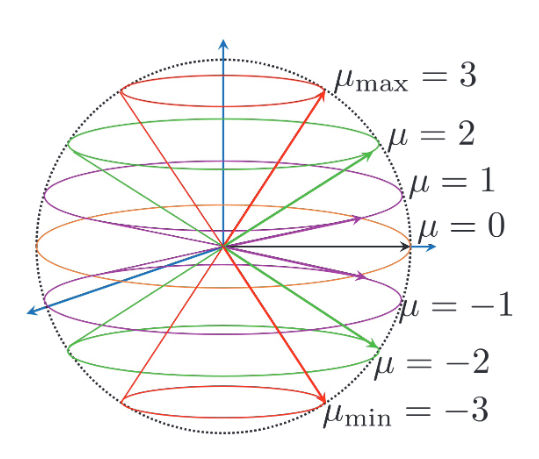
\(z\)方向的角动量算符的本征值存在取值范围\(-n / 2 \leqslant \mu \leqslant n / 2\),\(n \in \mathbb{N}\)。考虑阶梯算符会改变\(\widehat L_z\)的本征值。由于\(\mu^2<\lambda^2\),一定存在\(\mu\)的最大值和最小值:
\[ \\\begin{aligned} & \widehat{L}_{+}\left|\lambda^2, \mu_{\max }\right\rangle=|\varnothing\rangle \\ & \widehat{L}_{-}\left|\lambda^2, \mu_{\min }\right\rangle=|\varnothing\rangle \end{aligned} \]
根据已有的性质,可知:
- \(\mu_{\min }=-\mu_{\max }\)
- \(\mu_{\max }=\mu_{\min }+n \quad \text { with } n \in \mathbb{N}\)
从而可以得到:\(-n / 2 \leqslant \mu \leqslant n / 2\)。
对于\(\lambda\)为固定值的系统:
本征函数:球谐函数
球坐标系
考虑将角动量的三个分量转化到球坐标系:
\[ \begin{aligned}& \widehat{L}_x=i \hbar\left(\sin \varphi \frac{\partial}{\partial \theta}+\frac{\cos \varphi}{\tan \theta} \frac{\partial}{\partial \varphi}\right) \\& \widehat{L}_y=i \hbar\left(-\cos \varphi \frac{\partial}{\partial \theta}+\frac{\sin \varphi}{\tan \theta} \frac{\partial}{\partial \varphi}\right) \\& \widehat{L}_z=-i \hbar \frac{\partial}{\partial \varphi}\end{aligned} \]
→ 引:从直角坐标系到球坐标系的转换矩阵:
\[ \left(\begin{array}{l}\partial / \partial r \\\partial / \partial \theta \\\partial / \partial \varphi\end{array}\right)=\left(\begin{array}{ccc}\sin \theta \cos \varphi & \sin \theta \sin \varphi & \cos \theta \\r \cos \theta \cos \varphi & r \cos \theta \sin \varphi & -r \sin \theta \\-r \sin \theta \sin \varphi & r \sin \theta \cos \varphi & 0\end{array}\right)\left(\begin{array}{l}\partial / \partial x \\\partial / \partial y \\\partial / \partial z\end{array}\right) \]
角量子数和磁量子数
结论1:\(\widehat{L}_z\)的特征值是\(\hbar\)的整数倍
球坐标系下的\(\widehat{L}_z\)被表示为:\(-i \hbar \frac{\partial}{\partial \varphi}\)。假设函数\(\psi_{\mu_{\max }, \mu}(\theta, \varphi)\)是\(\widehat{L}_z\)的本征函数\(\psi_{\mu_{\max }, \mu}(\theta, \varphi)=\left\langle\theta, \varphi \mid \mu_{\max }, \mu\right\rangle\)。则有:
\[ -i \hbar \frac{\partial}{\partial \varphi} \psi_{\mu_{\max }, \mu}(\theta, \varphi)=\mu \hbar \psi_{\mu_{\max }, \mu}(\theta, \varphi) \]
一种非退化的解的形式为:
\[ \psi_{\mu_{\max }, \mu}(\theta, \varphi)=A_{\mu_{\max }, \mu}(\theta) \exp (i \mu \varphi) \]
在三维空间中,围绕\(z\)轴旋转\(2\pi\),空间不发生变换。表现相同对称性的条件是: \(\psi_{\mu_{\max }, \mu}(\theta, \varphi+2 \pi)=\psi_{\mu_{\max }, \mu}(\theta, \varphi)\) 。条件 \(\exp (i 2 \mu \pi)=1\) 只有在 \(\mu \in \mathbb{Z}\) 时才能满足。因此\(\widehat{L}_z\)的特征值必须是整数。
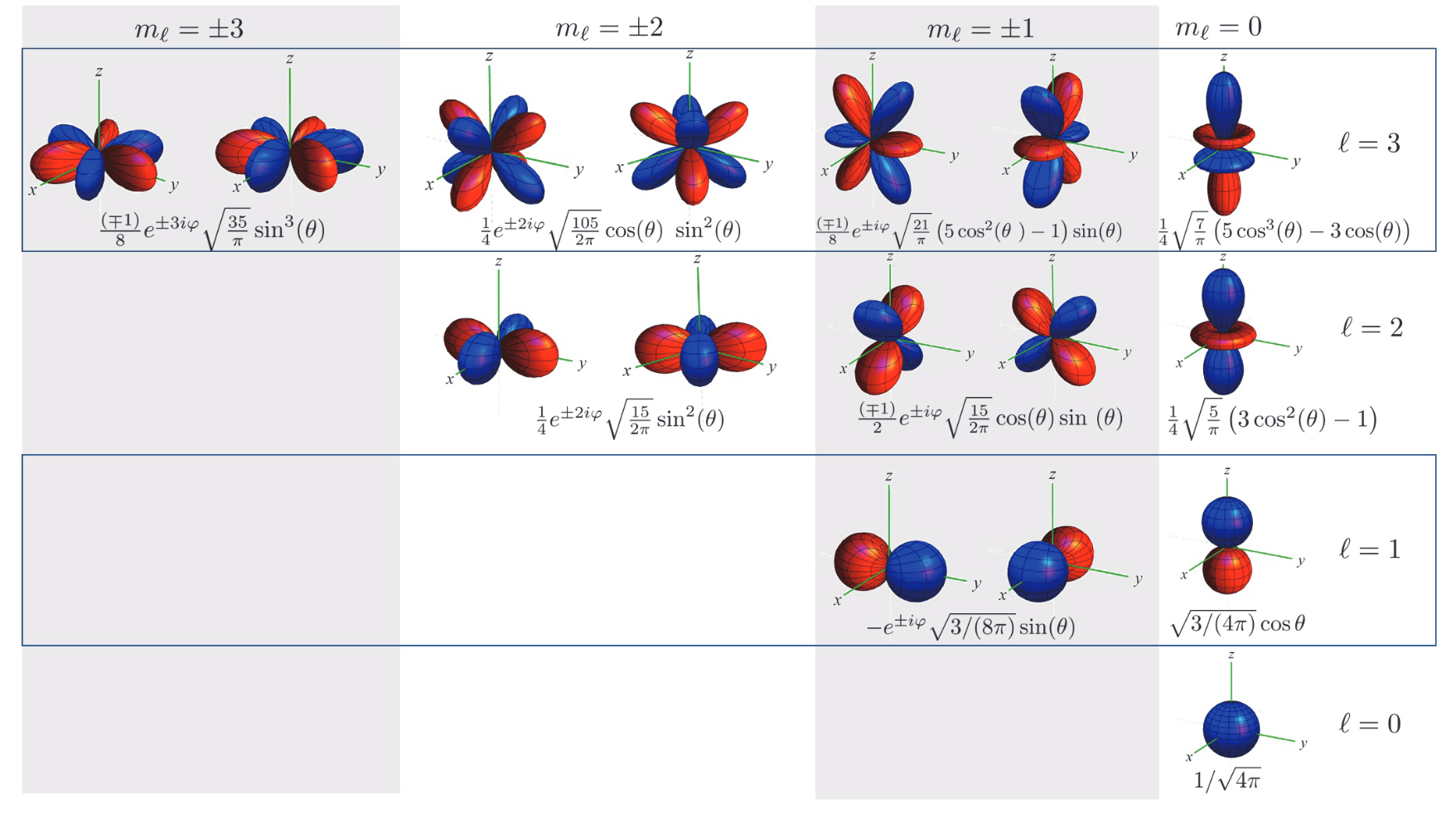
设\(\mu_{max} =l,\mu = m_l\),\(\widehat{L}^2\)和\(\widehat{L}z\)共享的本征态可以写成\(\left|\ell, m{\ell}\right\rangle\),其中\(-|\ell| \leqslant m_{\ell} \leqslant |\ell|\)。其中\(l\)被称为角量子数nombre quantique orbital,\(m_l\)被称为磁量子数nombre quantique magnétique。
🐈⬛ 值得注意的是,在这种定义下,原本的\(\lambda^2 = l(l+1)\)
球谐函数
结论2:CSCO\(\left\{\widehat{L}^2, \widehat{L}_z\right\}\)的特征函数是球谐函数
\[ \begin{aligned}Y_{\ell}^{m_{\ell}}(\theta, \varphi)= & \frac{(-1)^{\ell+m_{\ell}}}{2^{\ell} \ell!} \sqrt{\frac{(2 \ell+1)}{4 \pi} \frac{\left(\ell-m_{\ell}\right)!}{\left(\ell+m_{\ell}\right)!}} \times \exp \left(i m_{\ell} \varphi\right) \sin _{\ell}^m \theta \frac{d^{\ell+m_{\ell}}}{d(\cos \theta)^{\ell+m_{\ell}}} \sin ^{2 \ell} \theta\end{aligned} \]
已知\(\widehat{L}_{+}|\ell, \ell\rangle=|\varnothing\rangle\),代入\(\widehat L_x\)和\(\widehat L_y\)在球坐标系的表述,有:
\[ \hbar e^{i \varphi}\left(\frac{\partial}{\partial \theta}+\frac{i}{\tan \theta} \frac{\partial}{\partial \varphi}\right) \psi_{\ell, \ell}(r, \theta, \varphi)=0 \]
同时根据\(\psi(\theta, \varphi)=A(\theta) \exp (i l \varphi)\),有:
\[ e^{i(\ell+1) \varphi}\left(\frac{\partial}{\partial \theta}-\frac{\ell}{\tan \theta}\right) A(r, \theta)=0 \]
可得一个解:
\[ \psi_{\ell, \ell}(r, \theta, \varphi)=f(r) Y_{\ell}^{\ell}(\theta, \varphi)\ with \ Y_{\ell}^{\ell}(\theta, \varphi)=c_{\ell} e^{i \ell \varphi} \sin ^{\ell} \theta \]
然后在这个解上应用降算子即可得到其他磁量子数对应的解:
\[ Y_{\ell}^{m_{\ell}}(\theta, \varphi) \propto \underbrace{\left[e^{-i \varphi}\left(\frac{\partial}{\partial \theta}-\frac{i}{\tan \theta} \frac{\partial}{\partial \varphi}\right) \cdots e^{-i \varphi}\left(\frac{\partial}{\partial \theta}-\frac{i}{\tan \theta} \frac{\partial}{\partial \varphi}\right)\right]}_{\ell-m_{\ell} \text { times }} Y_{\ell}^{\ell}(\theta, \varphi) \]
最终解可以写作:
\[ y_{\ell, m_{\ell}}(\theta, \varphi)= \begin{cases}\frac{1}{\sqrt{2}}\left[Y_{\ell}^{-\left|m_{\ell}\right|}(\theta, \varphi)+(-1)^{m_{\ell}} Y_{\ell}^{\left|m_{\ell}\right|}(\theta, \varphi)\right] & \text { si } m_{\ell}>0 \\ Y_{\ell}^0(\theta, \varphi) & \text { si } m_{\ell}=0 \\ \frac{i}{\sqrt{2}}\left[Y_{\ell}^{-\left|m_{\ell}\right|}(\theta, \varphi)-(-1)^{m_{\ell}} Y_{\ell}^{\left|m_{\ell}\right|}(\theta, \varphi)\right] & \text { si } m_{\ell}<0\end{cases} \]
角动量例题:证明方法
角动量算子



