平衡级和精馏原理
平衡级和精馏原理
### 平衡级/接触级
不平衡的气液两相接触,经足够长时间弛豫,离开时,气液两相达到平衡的过程被称为平衡级。
在平衡过程中,选择较高的气象温度高,液相温度较低的组成。在平衡后易挥发组分A将从液相转移到气象,同时难挥发组分B从汽相转移到了液相。即汽相 浓度得到提浓,而液相浓度得到减浓。
# 精馏
精馏利用平衡级原理,多次通过平衡级来实现物质的高纯度分离。
精馏段和提馏段示意图
全塔物料衡算
总物料守恒方程和易挥发物物料守恒。
\[ \left\{\begin{array}{l}\boldsymbol{F}=\boldsymbol{D}+\boldsymbol{W} \\\boldsymbol{F} \boldsymbol{x}_F=\boldsymbol{D} \boldsymbol{x}_{\boldsymbol{D}}+\boldsymbol{W} \boldsymbol{x}_{\boldsymbol{W}}\end{array}\right. \]
可得各组分质量分率:
\[ \begin{align}\eta_{易挥发} & =\frac{D x_D}{F x_F} \times 100 \% \\\eta_{难挥发} & =\frac{W\left(1-x_W\right)}{F\left(1-x_F\right)} \times 100 \%\end{align} \]
全塔物料衡算示例
一精馏塔用于分离乙苯-苯乙烯混合物,进料量3100kg/h,其中乙苯的质量分率为0.6,塔顶、塔底产品中乙苯的质量分率分别要求为0.95、0.25, 求塔顶、塔底产品的质量流量和摩尔流量。
将两质量分率直接代入\((1),(2)\)中,可得:
\[ \begin{aligned}&Dx_D = 1767kg/h\\&W(1-x_w) = 806kg/h\Rightarrow3100-D+Dx_D-3100\times0.6 = 806\Rightarrow\\&D = 2201kg/h, W = -899kg/h\end{aligned} \]
分别代入两者得摩尔质量即可求摩尔流量。
精、提馏段物料衡算
🕍
精馏段的主要目的是增加混合物中所需组分的纯度。
提馏段的主要目的是去除混合物中的轻质组分,以提高底部产品中重质组分的纯度。
精馏段和提馏段
精馏段操作线方程
根据精馏段物料守恒和易挥发物质守恒:
\[ \left\{\begin{array}{l}V=L+D \\V y_{n+1}=L x_n+D x_D\end{array}\right. \]
其中,V为进入精馏段的物料,L为回流的物料,D为离开精馏段的物料。注意,物质流被假设始终守恒。
设回流比:
\[ R=\frac{L}{D} \]
将回流比代入物料守恒式:
\[ \left\{\begin{array}{l}L=R D \\V=(R+1) D\end{array}\right. \]
然后将结果代入易挥发组分守恒式,即可得到精馏段操作线方程。
\[ \begin{align}y_{n+1}=\frac{L}{V} x_n+\frac{D}{V} x_D\Longrightarrow y_{n+1}=\frac{R}{R+1} x_n+\frac{x_D}{R+1}\end{align} \]
关注提馏段操作线方程,发现其始终过定点\(\left(\mathbf{x}_{\mathbf{D}}, \mathbf{x}_{\mathbf{D}}\right)\),且有截距\(\frac{x_D}{R+1}\)。将其绘制:
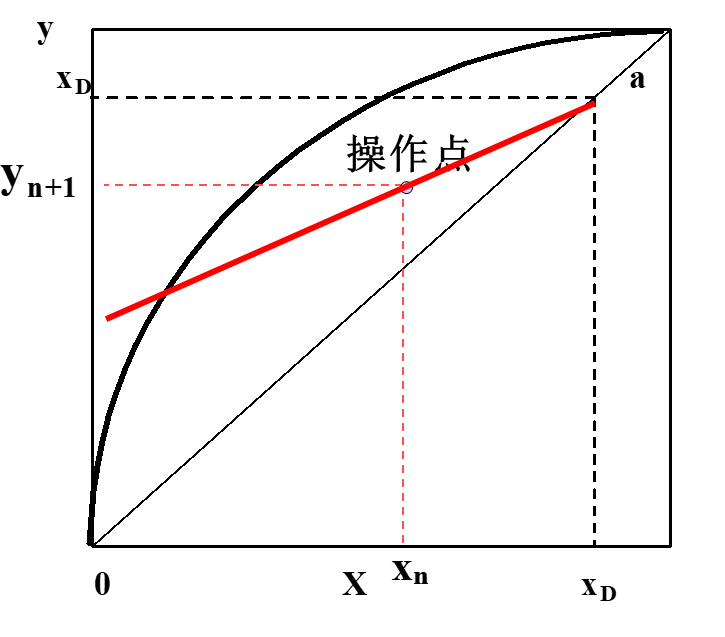
回流比增大,操作线斜率也将增大,意味着经过一块理论板后,汽相的增浓程度变大,液相的减浓程度变大。故操作线斜率大对精馏段的分离是有利的 。
精馏段操作线方程例题
苯-甲苯精馏塔的塔顶产品\(x_D=0.95\)(摩尔分率),回流比R=2。求从第二层理论塔板上升的蒸汽组成\(y_2\)。
应用上一章的方程\((3)\),可得:
\[ \begin{aligned}y_1=y_D=\frac{\alpha x_1}{1+(\alpha-1) x_1}\end{aligned} \]
代入本章方程\((3)\),可得:
\[ y_2 = \frac{R}{R+1}x_1+\frac{x_D}{R+1} \]
从第一个方程求出\(x_1\),代入第二个方程即可得到答案。
提馏段操作线方程
物料衡算:
\[ \left\{\begin{array}{l}L^{\prime}=V^{\prime}+W\\L^{\prime} x_m=V^{\prime} y_{m+1}+Wx_W\end{array}\right. \]
得到提馏段的操作线方程:
\[ y_{m+1}=\frac{L^{\prime}}{V^{\prime}} x_m-\frac{W x_W}{V^{\prime}} \]
提馏段操作线方程过定点\(\left(\mathbf{x}_{\mathbf{W}}, \mathbf{x}_{\mathbf{W}}\right)\),且具备截距\(-\frac{W x_W}{V^{\prime}}\)。

与精馏段类似,斜率小,远离平衡线,塔板的分离能力高,对精馏有利。
进料情况和加料线方程
进料情况
五种进料情况
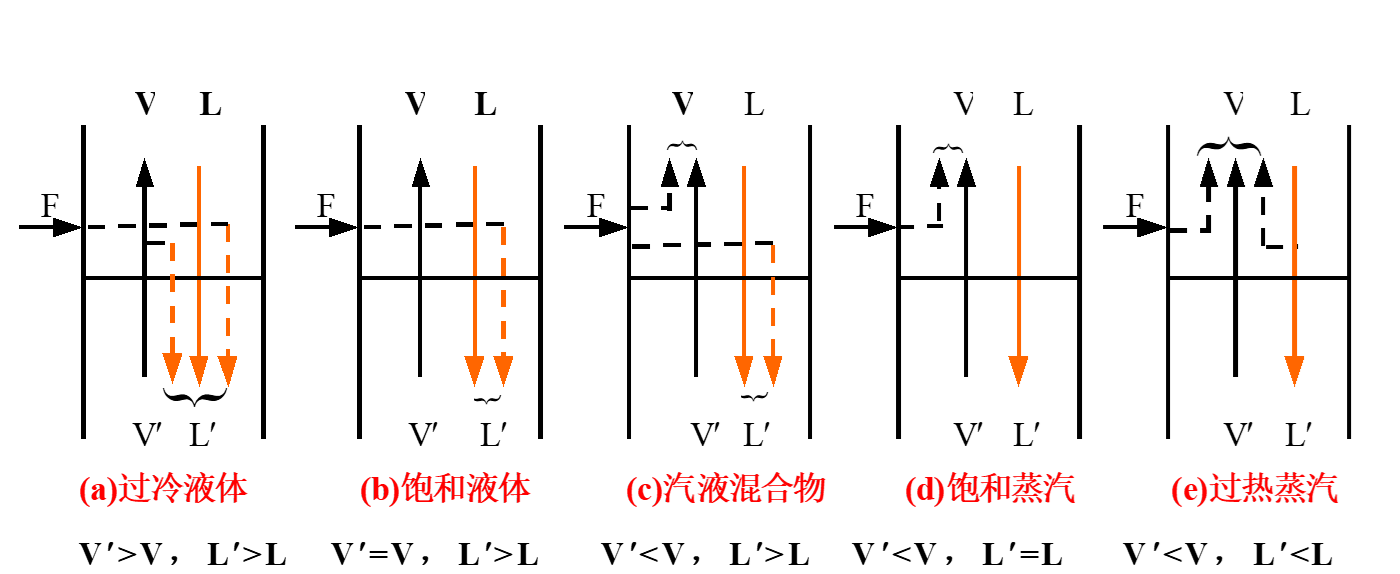

物料衡算和热量衡算:
\[ \begin{array}{l} F + L + V' = L' + V \Rightarrow V-V^\prime = F+L-L^\prime\\ Fi_i + Li_i + V'i_i' = L'i_i' + Vi_i \end{array} \]
其中,\(i\)表示每个物质摩尔焓。近似认为\(i_L \approx i_L^{\prime}, \quad i_V \approx i_V^{\prime}\),即可得到进料热状态参数。
\[ q = \frac{L^{\prime}-L}{F}=\frac{i_V-i_F}{i_V-i_L} = \frac{从进料状态变为饱和蒸汽所需热量}{气化潜热} \]
由此,可以得到:
\[ \begin{align}\left\{\begin{array}{l}L^{\prime}=L+q F \\V^{\prime}=V+(q-1) F\end{array}\right.\end{align} \]

加料线方程
跟据之前的推导有:
\[ \begin{aligned} & V y=L x+D x_D \\ & V^{\prime} y=L^{\prime} x-W x_W \end{aligned} \]
跟据\((4)\),将\(L^\prime\)和\(V^\prime\)代换,得到加料线方程,即Q线方程:
\[ \begin{align}y=\frac{q}{q-1} x-\frac{x_F}{q-1}\end{align} \]
[{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fchempro-3%2FUntitled_11.png","alt":""},{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fchempro-3%2FUntitled_12.png","alt":""}]
|
由右图可见,加料线,精馏段操作线和提馏段操作线可以由推一。\(q\)越小,提馏段操作线越靠近平衡新,对系统越为不利。
综合考虑加料线,精馏段操作线和提馏段操作线的例子
一常压精馏塔的进料为组成0.44(摩尔分率)的苯-甲苯混合物,求在下述进料状况下的q值及q线斜率(1)汽、液的摩尔流率各占一半;(2)20℃;(3)180℃。已知在涉及的温度范围内,苯和甲苯液体的平均比热Cp,L=0.44kcal/kg℃,其蒸汽的平均比热Cp,V=0.30kcal/kg℃;在总压P=1atm的沸点下,苯的汽化潜热rA=94.2kcal/kg,甲苯的汽化潜热rB=86.5kcal/kg。
- \(i_V-i_L = r_A\times0.44+r_B\times (1-0.44)\)
- 平均分子质量:\(M_{苯-甲苯} =0.44M_{苯}+(1-0.44)M_{甲苯}\)
- 汽、液的摩尔流率各占一半,\(i_V-i_F = 0.5\times(i_V-i_L)\) ,\(q = 0.5\)
- \(20\)摄氏度时,进料处于过冷状态,首先将其加热至饱和,再蒸发至气体,\(i_V-i_F = 0.44\times M_{苯-甲苯}\times (T_{泡点}-20)+i_V-i_L\),\(q>1\)
- \(180\)摄氏度时,进料处于过热状态,首先将其冷却至饱和,\(i_V-i_F = 0.30\times(T_{露点}-180)\times M_{苯-甲苯}\),\(q<0\)
图解法求理论塔板数
- 首先绘制精馏段、提馏段操作线和加料线,标出b点,d点和a点。
- 然后,从点a开始,再精馏线或提馏线之间画阶梯。
- 直到接替跨过b点为之。
每个阶梯的竖直部分即代表塔板。跨过b点的塔板是再沸器,跨过d点的塔板是加料板。
- 最终,理论塔板数是所画的总阶梯数-1,可以为非整数。
- 精馏段板数和提馏段板数都可以是非整数。
- 但加料板所在位置是整数,加料板所在位置实际上代表需要最少的塔板(阶梯)的位置。
- 于平衡线交点\(i\)所连接的横线的\(y\)值为\(y_i\),所连接的竖线的\(x\)值为\(x_i\)
塔板效率和实际塔板数
🕍 塔板效率包括单板效率和全塔效率
单板效率
单板效率也被称为默弗里板效,其定义如下:
\[ \begin{align}&E_{m V}=\frac{\text{汽相实际增浓程度}}{\text{汽相理论增浓程度}}=\frac{y_{n}-y_{n+1}}{y_n^*-y_{n+1}}\\&E_{m L}=\frac{\text{液相实际减浓程度}}{\text{液相理论减浓程度}}=\frac{x_{n-1}-x_{n}}{x_{n-1}-x^*_{n}}\end{align} \]
全塔效率
全塔效率又称总板效率:
\[ E_0=\frac{\text { 理论板数 }}{\text { 实际板数 }}=\frac{N}{N_e} \]
全塔效率大,则单板效率一定大,反之不一定。
回流比选取
理想回流比
理想回流比是由于回流比上升会使设备费下降,能源费上升。因此,两者的平衡点即为理想回流比。
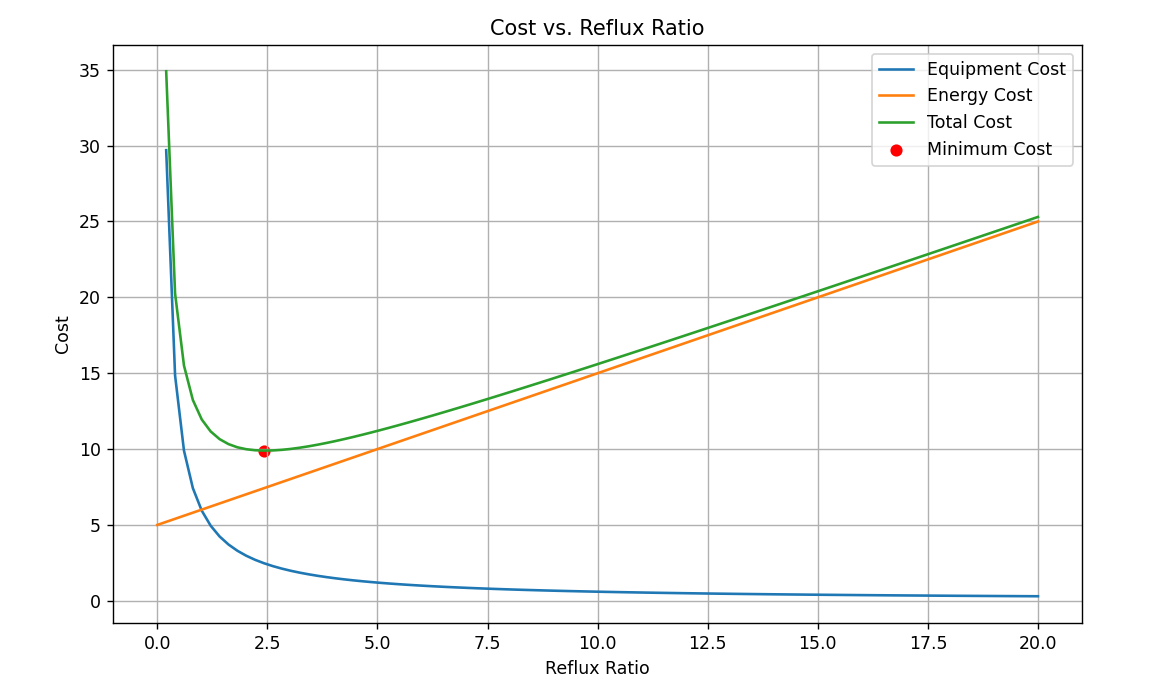
大部分时候理想回流比是跟据生产经验选择的,一般选取:
\[ R_{o p t}=(1.1 \sim 2) R_{\min } \]
最小回流比
为完成某一分离任务,所需的理论塔板数为无穷多时的回流比称为最小回流比。通过选择回流比,使得提馏段和精馏段操作线以及进料线三线交点在平衡曲线上时的回流比称为最小回流比。此时,需要无穷个塔板才能完成精馏。

最大回流比
最大回流比时,理论塔板数最小。此时全回流。
总结
- 相平衡关系
\[ y = \frac{\alpha x}{1+(\alpha-1)x} \]
- 全塔物料衡算
\[ \begin{aligned}&F = D+W\\&Fx_F = Dx_D+Wx_w\end{aligned} \]
- 操作线方程
\[ \begin{aligned}&y_{n+1} = \frac{R}{R+1}x_n+\frac{x_D}{R+1}\\ &y_{m+1} = \frac{L^\prime}{V^\prime}x_m+\frac{W}{V^\prime}x_W\\& y = \frac{q}{q-1}x-\frac{x_F}{q-1}\end{aligned} \]
- 塔板上的方程
\[ \left\{\begin{array} { l } { L = R D } \\{ V = ( R + 1 ) D }\end{array} \quad \left\{\begin{array}{l}L^{\prime}=L+q F \\V^{\prime}=V+(q-1) F\end{array}\right.\right. \]