蒸馏基本概念和基础的蒸馏方式
蒸馏基本概念和基础的蒸馏方式
基本概念
蒸馏的分类
- 二元蒸馏,多元蒸馏
- 连续蒸馏,间歇蒸馏
- 常压蒸馏,加压蒸馏,减压蒸馏
- 简单蒸馏,平衡蒸馏,精馏
二元理想物系气液相平衡
由理想气体和理想溶液总成的体系称为理想气液物系。
理想气体
满足理想气体状态方程,道尔顿分压定律
\[ P=p_A+p_B \quad y_A=\frac{p_A}{P} \quad y_B=\frac{p_B}{P} \]
理想溶液
满足拉乌尔定律的溶液称为理想溶液
\[ \left\{\begin{array}{l}p_A=p_A^0 x_A \\p_B=p_B^0 x_B\end{array}\right. \]
理想物系的气相/液相组成方程
对于理想物系,气相满足:
\[ P=p_A+p_B=p ^0_A x+p_B^0(1-x) \]
可得:
\[ \begin{align}\left\{\begin{aligned}& x=\frac{P-p_B^0}{p_A^0-p_B^0} \\& y=\frac{p_A}{P}=\frac{p_A^0 x}{P}=\frac{p_A^0}{P} \frac{P-p_B^0}{p_A^0-p_B^0}\end{aligned}\right.\end{align} \]
理想物系气液平衡相图

图中dew point为露点,bubble point为泡点。
- 露点线:表示在给定的气压下,空气中的水汽达到饱和所需要的温度。当空气中的水汽含量增加时,露点线对应的温度也会增加。
- 泡点线:与露点线类似,但是它是在给定的水汽含量下,水在空气中达到饱和所需的温度。也就是说,泡点线表示了水蒸气在一定含量下凝结成水的温度。
露点线上方为气相区,下方为液相区,包围的区域为两相区,其成分组成可以通过所处相图中的点到露点线和泡点线的距离\(L_d\)和\(L_b\)来计算:
\[ \begin{align}n_l\cdot L_b = n_g\cdot L_d\end{align} \]
详见热力学笔记中的相图部分。
挥发度和相对挥发度
挥发度是液体蒸汽压和液相组成之比:
\[ v_A=\frac{p_A}{x_A} \quad v_B=\frac{p_B}{x_B} \]
理想溶液的挥发度即为\(p^0\)。
相对挥发度是两个组分挥发度之比:
\[ \alpha=\frac{v_A}{v_B}=\frac{p_A / x_A}{p_B / x_B}=\frac{y_A / x_A}{y_B / x_B} \]
对于理想物系,相似挥发度可认为不是温度的函数。
参考:苯-甲苯物系的相对挥发度表
\[ \begin{array}{|c|c|c|c|c|c|c|c|c|c|} \hline t^{\circ} \mathrm{C} & 80.1 & 84 & 88 & 92 & 96 & 100 & 104 & 108 & 110.8 \\ \hline \mathrm{P}_{\mathrm{A}}{ } \mathrm{mmHg} & 760 & 856 & 963 & 1081 & 1210 & 1350 & 1502 & 1668 & 1783 \\ \hline \mathbf{P}_{\mathrm{B}}{ }{\mathrm{mmHg}} & 292 & 334 & 381 & 434 & 492 & 556 & 627 & 705 & 760 \\ \hline x & 1 & 0.816 & 0.651 & 0.504 & 0.373 & 0.257 & 0.152 & 0.057 & 0 \\ \hline y & 1 & 0.919 & 0.825 & 0.717 & 0.594 & 0.456 & 0.300 & 0.125 & 0 \\ \hline \text { a } & 2.60 & 2.56 & 2.53 & 2.49 & 2.46 & 2.43 & 2.40 & 2.37 & 2.35 \\ \hline \end{array} \]
相似挥发度和某一组分在液相中占比
对于A的液相组成,有:
\[ \alpha = \frac {y/x}{(1-y)/(1-x)} \]
解得:
\[ \begin{align}y=\frac{\alpha x}{1+(\alpha-1) x}\end{align} \]
理想物系x-y相图
左图以上表为例的苯-甲苯x-y相图,描点画出即可。
- \(y≥x\) 故有曲线一定在对角线上方
- \(\alpha\)越大,相平衡曲线相距对角线约远,汽液相平衡时汽、液两相组成的差异愈大,越有利于蒸馏
右图为乙醇-水x-y相图,为非理想物系,可做参考。
基础的蒸馏方式
简单蒸馏
简单蒸馏是一种非连续,分离程度不高得蒸馏方式。
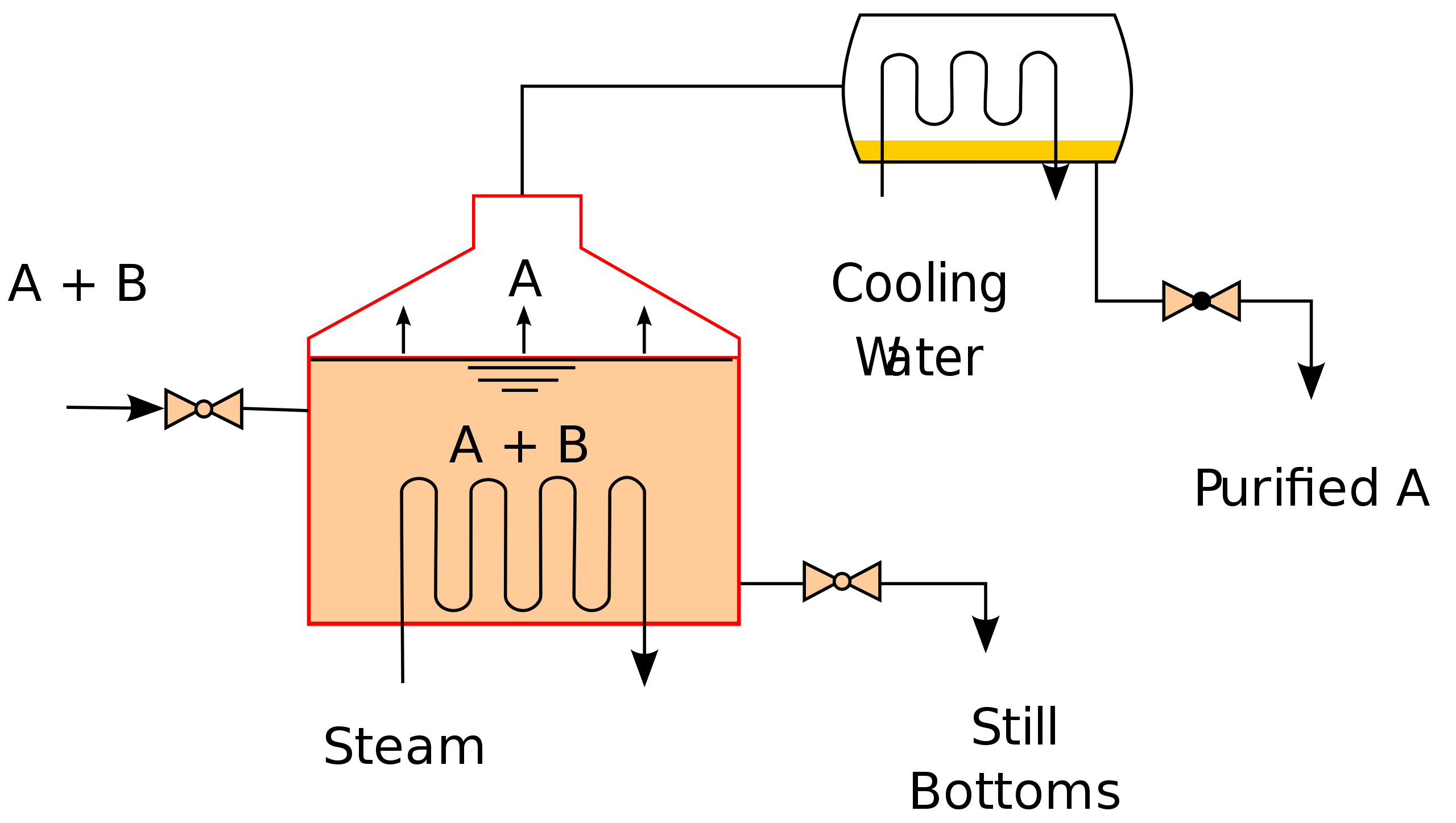
记蒸发前液量为\(W_1\)蒸发后液量为\(W_2\),蒸发出的液量为\(W_D\),蒸发出液体中易挥发组分比例为\(x_D\)。
物料衡算
- 总物料守恒:\(W_1=W_2+W_D\)
- 易挥发物质物料守恒:\(W_1 x_1=W_2 x_2+W_D x_D\)
- 公式\((2)\)在本问题中的表述:
\[ W_2\left(x_1-x_2\right)=W_D\left(x_D-x_1\right) \]
微分物料衡算:\(y d W=d(W x)=W d x+x d W\)
- 积分得:
\[ \ln \frac{W_1}{W_2}=\int_{x_2}^{x_1} \frac{d x}{y-x} \]
- 根据公式(3)有:
\[ \begin{align}\ln \frac{W_1}{W_2}=\int_{x_2}^{x_1} \frac{d x}{\frac{\alpha x}{1+(\alpha-1) x}-x}\end{align} \]
- 计算右侧积分:
\[ \begin{align*}\int \frac{d x}{\frac{\alpha x}{1+(\alpha-1) x}-x} &= \int-\frac{(\alpha-1) x+1}{(\alpha-1) x^2+(1-\alpha) x} d x\\ & = -\int \frac{(\alpha-1) x+1}{(\alpha-1)(x-1) x} d x\\ & = -\frac{1}{\alpha-1} \int \frac{1}{(x-1) x}+\frac{\alpha-1}{x-1} d x\\ & =\frac{\ln (|x|)}{\alpha-1}-\frac{\alpha \ln (|x-1|)}{\alpha-1} \end{align*} \]
- 因此有:
\[ ln \frac {W_1}{W_2} = \left[\frac{\ln (|x|)}{\alpha-1}-\frac{\alpha \ln (|x-1|)}{\alpha-1}\right]_{x_1}^{x_2} \]
由此,三个方程,三个未知数可解。
例1:苯-甲苯物系简单蒸馏
苯-甲苯溶液的初浓度\(x_1=0.4\),共\(10kmol,\) 在\(1atm\)下 进行简单蒸馏,到残液\(x_2=0.3\)为止。求馏出液的量和浓度,以及釜内溶液沸点的变化,\(\alpha = 2.46\)
\[ ln \frac {W_1}{W_2} = \left[\frac{\ln (|x|)}{\alpha-1}-\frac{\alpha \ln (|x-1|)}{\alpha-1}\right]_{x_1}^{x_2} = 0.457 \]
得:
\[ W_2 = 6.33kmol, \ W_D = W_1-W_2 = 3.67kmol \]
根据易挥发物质得物料守恒:
\[ x_D= 0.572 \]
此时沸点约为92℃左右。
平衡蒸馏
平衡蒸馏又称闪蒸,是一种连续,稳定,分离程度不高得蒸馏方式。
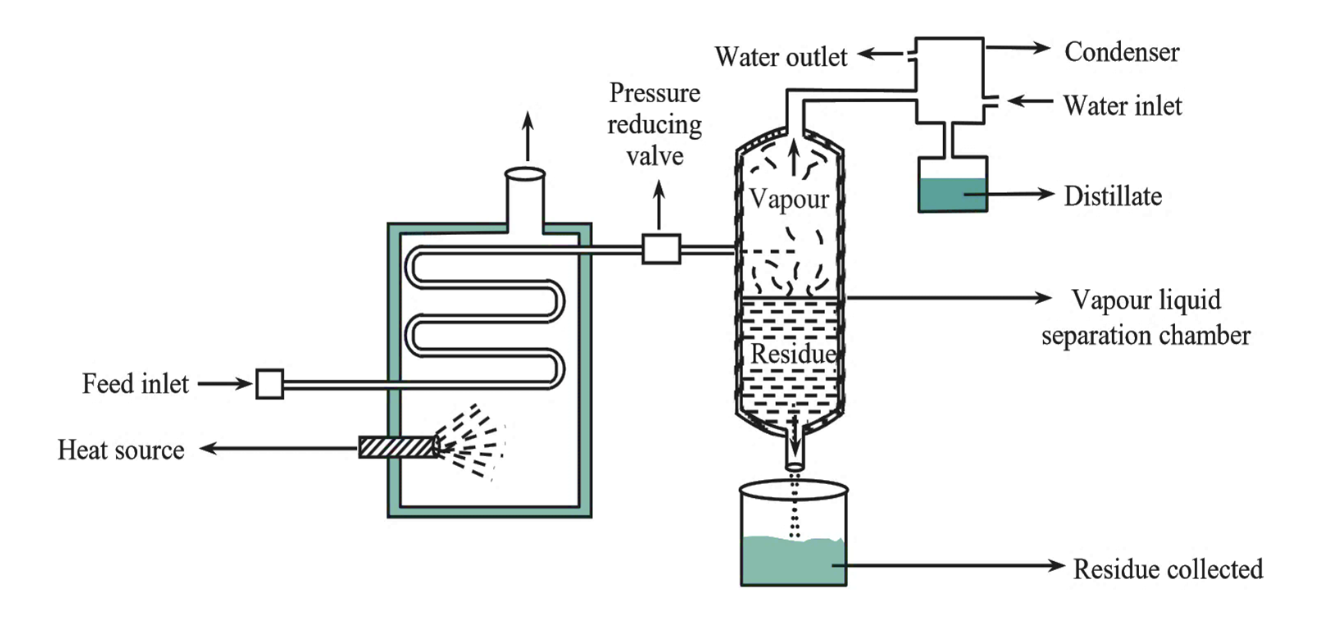
记闪蒸器物料输入为\(F\),液相输出为\(L\),气相输出为\(V\),液相易挥发成分占比\(x_W\),气相易挥发成分占比\(y_D\)
分率
分率是闪蒸器输出在输入中的占比
- 液相分率 \(q=\frac{L}{F}\)
- 气相分率 \(f=\frac{V}{F}\)
物料衡算
- 总物料守恒
\[ F = L+V \]
- 易挥发成分物料守恒
\[ F x_F=L x_W+V y_D \]
- 相平衡方程
\[ \begin{align}y_D=\frac{\alpha x_W}{1+(\alpha-1) x_W}\end{align} \]
- 公式\((2)\)在平衡蒸馏中的表述:
\[ L\left(x_F-x_W\right)=V\left(y_D-x_F\right) \]
- 方程联立可得:
\[ \begin{align}fy_D+(1-f) x_W=x_F\end{align} \]
例2:苯-甲苯物系闪蒸
料液为 \(\mathrm{x}_{\mathrm{F}}=0.4\) 的苯-甲苯溶液, 进行平衡蒸馏, 闪蒸塔中压力 \(P=1\) \(atm\)。试作图表示闪蒸后的汽、液组成 \(\mathrm{y}_{\mathrm{D}}, \mathrm{x}_{\mathrm{w}}\) 以及温度\(t\)随汽化分率f的变化关系,\(\alpha = 2.46\)。
代入\((5)\)式:
\[ y_D=\frac{\alpha x_W}{1+(\alpha-1) x_W} = 0.621 \]
带入\((6)式\):
\[ x_W = \frac{x_F-fy_D}{1-f} = \frac{0.4-0.621f}{1-f} \]
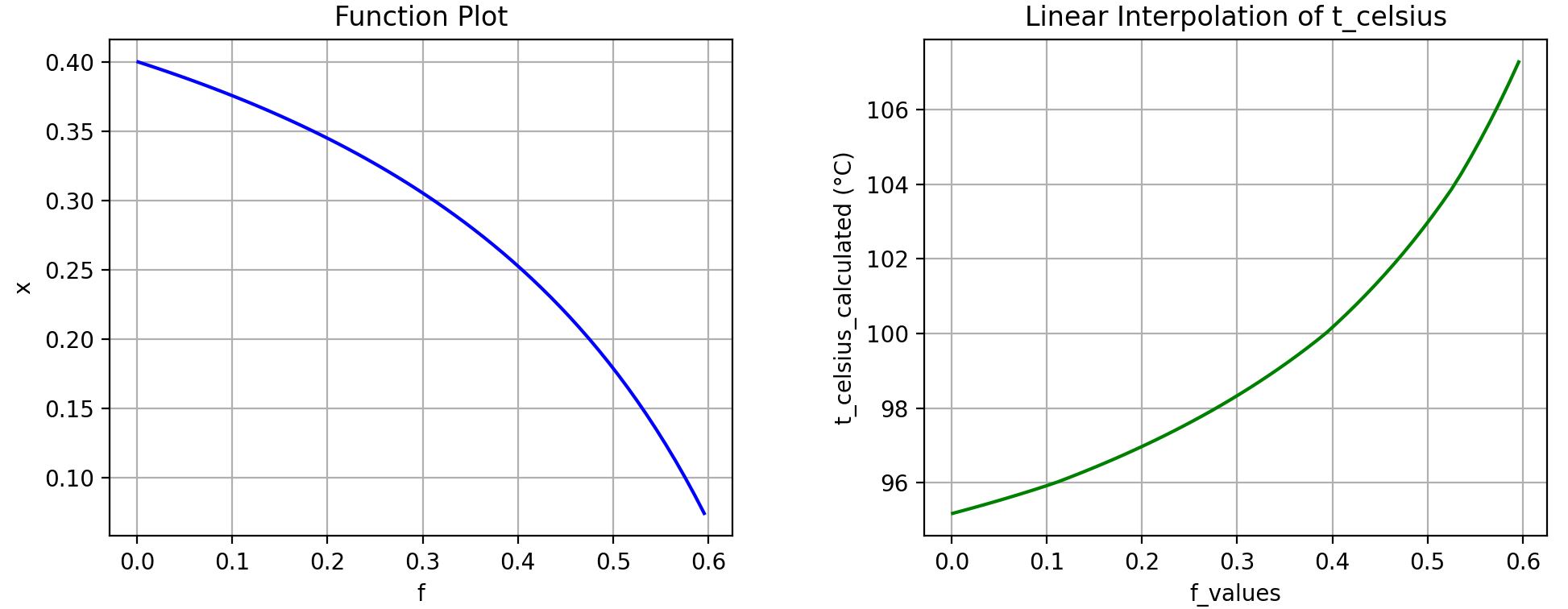
简单蒸馏和平衡蒸馏的比较
假设\(F = W_1\)和\(x_1 = x_F\),比较两种蒸馏的分离效果\((x_D, y_D)\)和产量\((W_D,V)\)。由下图简单蒸馏和平衡蒸馏的相图对比可见,\(y_D\)小于\(x_D\)所以简单蒸馏的分离效果更好。
根据物料守恒,可以推得:
\[ W_D=\frac{W_1\left(x_1-x_2\right)}{x_D-x_2},V=\frac{F\left(x_F-x_W\right)}{y_D-x_W} \]
可见平衡蒸馏的产量大。
经过多次蒸馏,简单蒸馏和平衡蒸馏都可以达到较高纯度,但是其能耗大,设备投资大和产量小的特点使其很难应用。