组合逻辑系统的缺陷&定时图&锁存器/触发器的技术实现
组合逻辑系统的缺陷&定时图&锁存器/触发器的技术实现
组合逻辑系统的缺陷
一个例子
考虑以下例子:
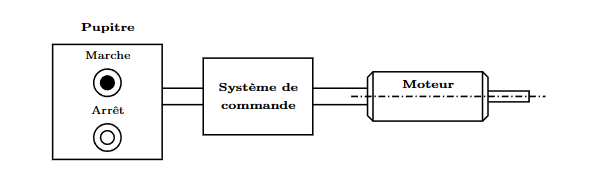
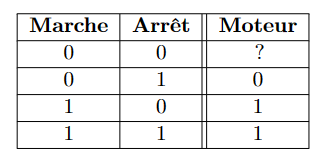
- 如果电机尚未运行,则按下启动按钮将触发电机旋转
- 如果电机已运行,则按下停止按钮将导致电机停止。
- 按启动按钮优先于按停止按钮。
- 取消按下按钮对系统没有影响
在真值表的后三种情况,我们很容易判断电机的状态。然而,两个输入都为 0 时的输出取决于电机的运行状态。
此时,组合逻辑系统不能简单地结果这个问题。
记忆系统的引入
为此,我们需要引入一个反映电机在时间t的运行情况的状态变量。我们可以称之为锁存器(Mémoire)。在这种情况下,我们可以定义逻辑表达式:
\[ \begin{align*}Moteur =& Marche \cdot \overline{Arrêt}+Marche \cdot \overline{Arrêt} + \overline{Marche }\cdot\overline{Arrêt}\cdot Mémoire\\= & \text { Marche }+\overline{\text { Marche }} \cdot \overline{\text { Arrêt }} \cdot \text { Mémoire }\\=&\text { Marche }+\overline{\text { Arrêt }} \cdot \text { Mémoire }\end{align*} \]
以及新的真值表。
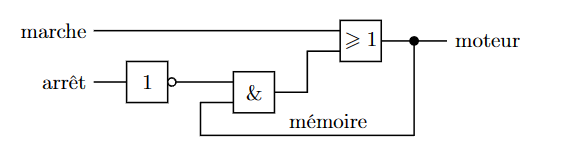
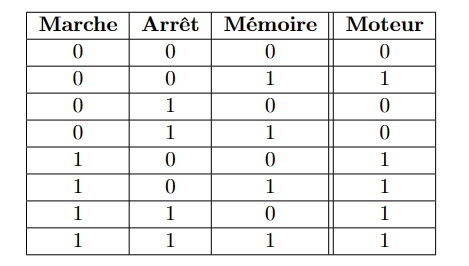
在新的流程图中,使用循环来表示寄存器。这种结构正是一般的时序系统结构。
定时图 Chronogramme
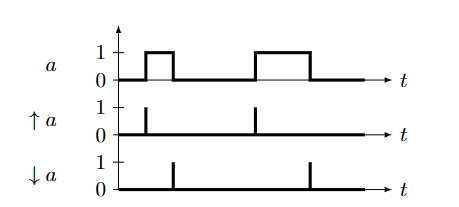
定时图是逻辑变量的时序表示。

上升沿和下降沿
上升沿:
\[ \uparrow a=\left\{\begin{array}{l}1 \quad 若a从0变为1\\0 \quad sinon\end{array}\right. \]
下降沿:
\[ \downarrow a=\left\{\begin{array}{l}1 \quad 若a从1变为0\\0 \quad sinon\end{array}\right. \]
锁存器/触发器(bascule)技术实现
RS锁存器 Bascules RS
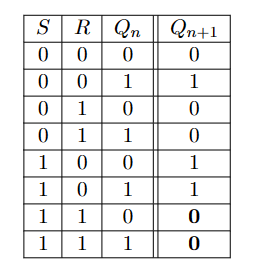
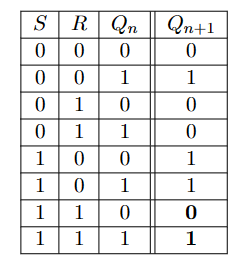
\(S\)(代表Set)记忆输入变量,\(R\)(代表Reset)记忆擦除输入变量,\(Q_{n+1}\)输出变量\(Q\)的当前状态,\(Q_n\)代表输出变量\(Q\)的先前状态
RS锁存器的真值表如下:
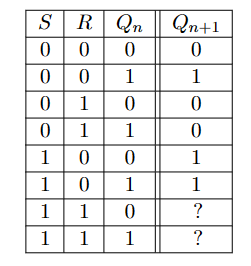
注意,当S和R都为真时,结果是不确定的。有时,这种情况被简单的禁止,在其他情况下,根据不同的处理方法,有三种RS锁存器类型。
- 激活优先的RS锁存器 à priorité à l’activation 先考虑激活信号,后考虑擦除信号
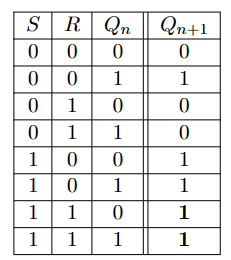
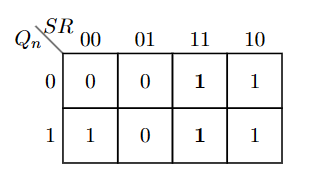
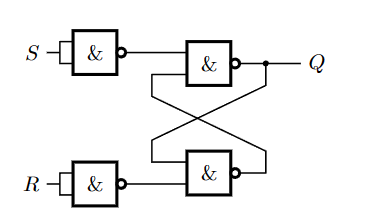
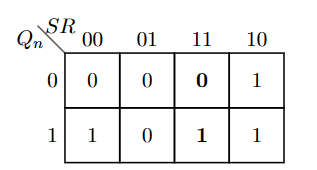
\(Q_{n+1}\)的表达式可以被记为:
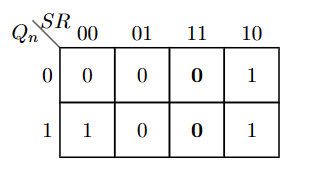
\[ Q_{n+1} = \bar S\bar RQ_n+S\bar R\bar Q_n+S\bar RQ_n+S R\bar Q_n+S R Q_n = S+\bar R Q_n=\overline{\overline{S+\bar{R} \cdot Q_n}}=\overline{\bar{S} \cdot \overline{\bar{R} \cdot Q_n}} \]
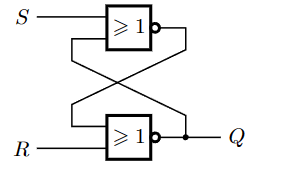
由此,可以设计如上第三张图的系统,用以实现RS锁存器。或者简记为:
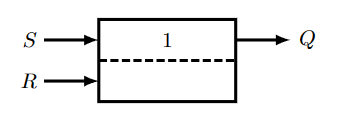
1代表S优先。下图为一幅讨论不同情况的定时图,可以参考:
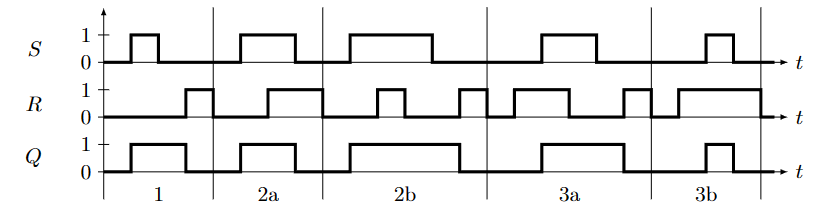
- 擦除优先的RS锁存器 à priorité à l’effacement 先考虑擦除信号,再考虑激活信号
真值表很好理解,不再赘述。为了实现这种RS锁存器,需使用两个或非门,其公式为:
\[ Q_{n+1}=\bar{R} \cdot\left(S+Q_n\right)=\overline{\overline{\bar{R}} \cdot\left(S+Q_n\right)}=\overline{R+\overline{S+Q_n}} \]
或表示为:
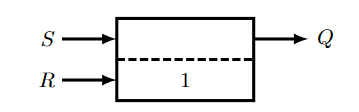
- 无源同时输入RS锁存器 à entrées simultanées passives 两信号同时输入时,\(Q_{n+1} = Q_n\)
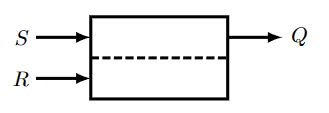
其表达式为:
\[ Q_{n+1}=\bar{R} \cdot S+\bar{R} \cdot Q_n+S \cdot Q_n=\bar{R} \cdot Q_n+S \cdot\left(Q_n+\bar{R}\right) \]
跟前两种情况非常相似不在赘述。
- 总的定时图:
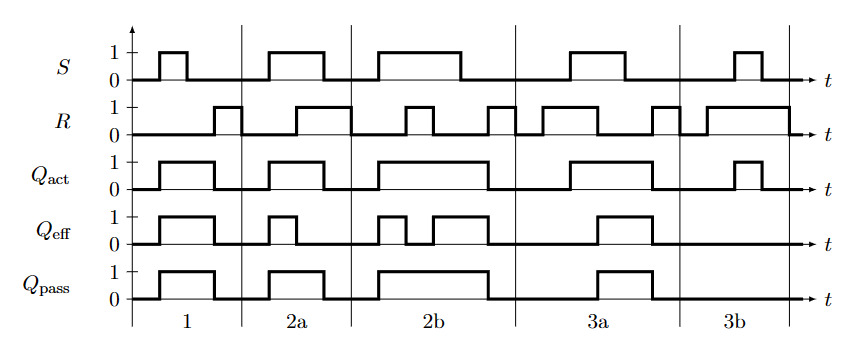
带验证的RS触发器 Bascules RS à validation
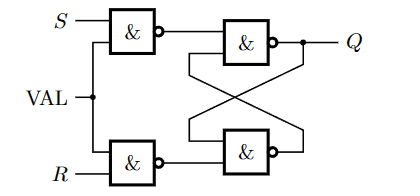
仅有VAL为正时,RS输入才会影响Q:
\[ \begin{aligned}Q_{n+1} & =\overline{\mathrm{VAL}} \cdot Q_n+\mathrm{VAL} \cdot\left(S+\bar{R} \cdot Q_n\right) \\& =\overline{\mathrm{VAL}} \cdot Q_n+\mathrm{VAL} \cdot S+\mathrm{VAL} \cdot \bar{R} \cdot Q_n \\& =\overline{\mathrm{VAL}} \cdot Q_n+\mathrm{VAL} \cdot S+\bar{R} \cdot Q_n\end{aligned} \]
JK触发器 Bascule JK
RS锁存器有一些缺点,RS锁存器直接由三个输入的电平决定,信号的变化仅取决于三个输入电平变化的速度,可能随时发生改变,即RS锁存器的变化是异步的。这在复杂系统中可能会导致不稳定。
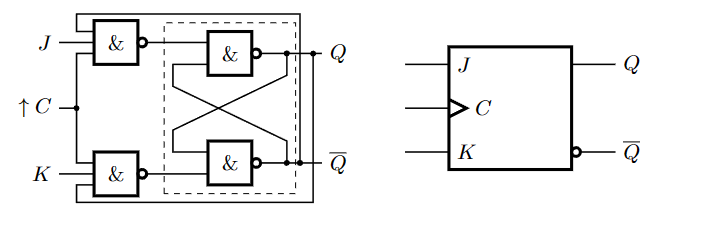
JK触发器是基于带验证的RS锁存器的改进,它引入了周期性的01交替信号,即始终信号作为VAL。它只在始终信号为1时更新状态,从而避免了随时可能发生的不稳定变化。由于时钟信号的引入,且状态随时钟信号上升沿变化,我们可能更倾向于称之为触发器而不是锁存器。
- 若\(\uparrow C = 0\),则无论JK信号如何,\(Q_{n+1} = Q_n\)
- 若\(\uparrow C = 1\),则信号变化取决于\(J,K,Q_n\)的值:
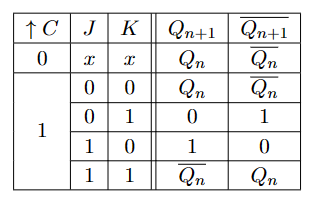
注意再JK都为1时,JK触发器的表现与RS不同,他会进行一个取反操作,即Régime de basculement。
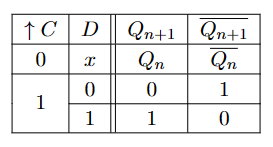
D触发器 Bascule D
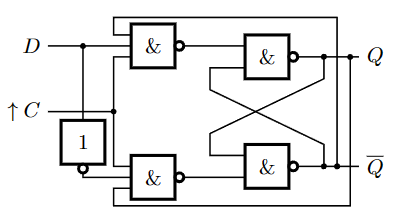
D触发器引入了了JK不相等的约束,并使用D来代表J的JK触发器。

锁存器/触发器的基本应用
分频器 Diviseur de fréquence

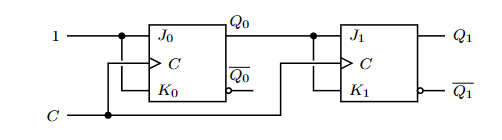
如果我们设置JK触发器的\(J = K = 1\),则JK触发器每次检测到时钟信号上升沿都会进行一次翻转,得到的Q的信号周期恰好为始终信号的两倍。因此,可以将n个\(J = K = 1\)的JK锁存器向量,实现时钟信号的分频:
\[ f_n = \frac 1 {2^n}f_C \]
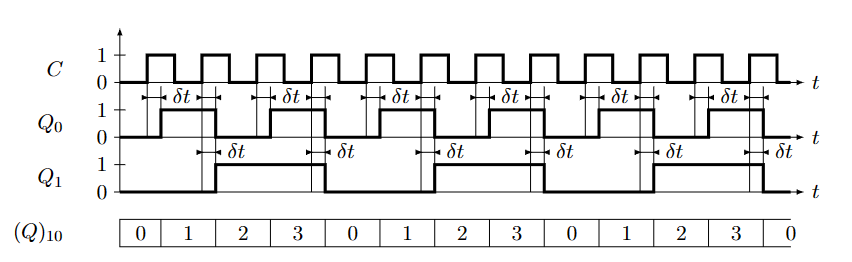
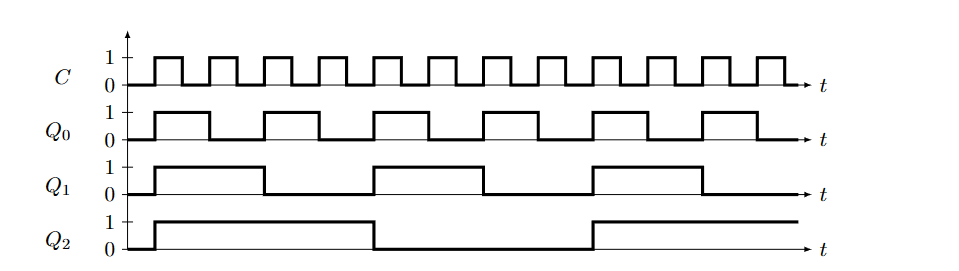
定时图如下:
异步计数器
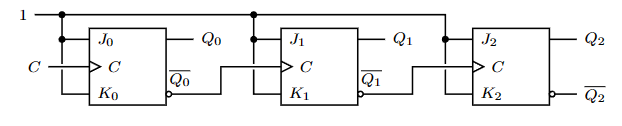
在相同的JK触发器设置下,将\(\bar Q_n\)作为下一个JK触发器的时钟信号而不是\(Q_n\)可以使系统作为异步计数器。比如一个三位的异步计数器:
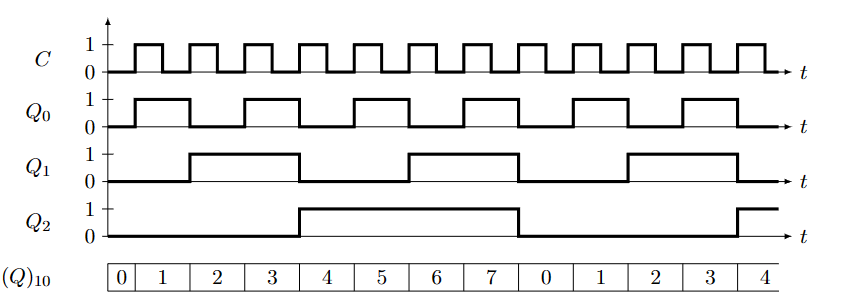
计数器的异步性体现在电信号的延迟中:
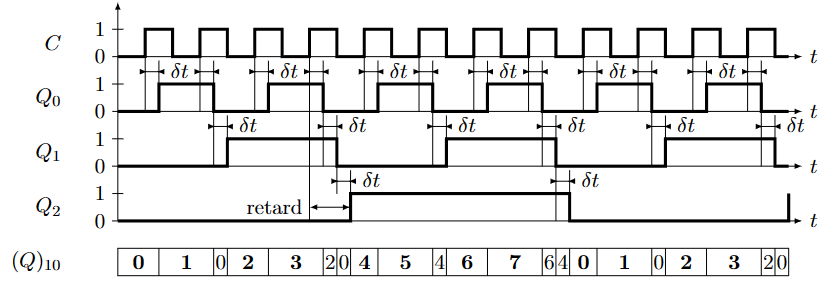
同步技术器
同步计数器将初始的时钟信号作为所有JK触发器的时钟信号,并将\(Q_0\)作为JK信号接入,使JK触发器在保持和反转两个状态下以\(Q_0\)的周期交替,从而起到计数的作用。在这种情况下延迟不再影响计数: