组合逻辑系统的例子 Exemples de systèmes combinatoires
组合逻辑系统的例子 Exemples de systèmes combinatoires
常见的组合逻辑系统
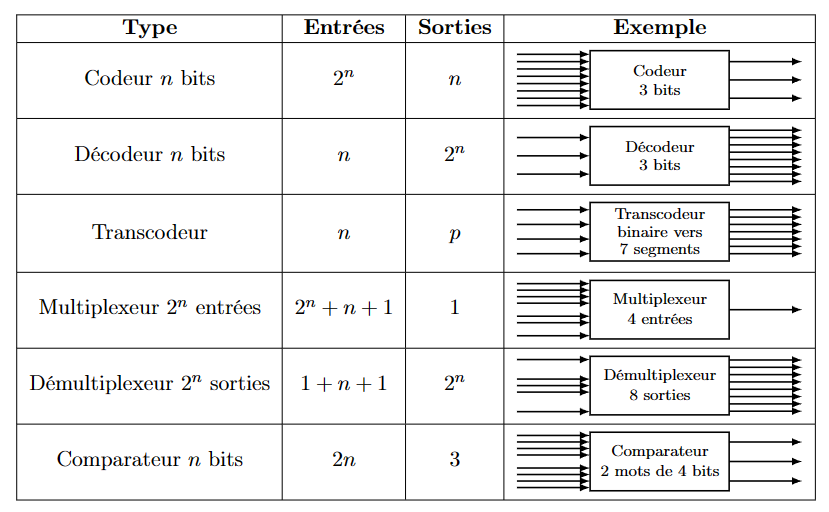
- n位编码器
- n位解码器
- 转码器
- \(2_n\)输入多路复用器
- \(2_n\)输出多路复用器
- n位比较器
编码器 codeur
例如,一个四位编码器最多可以转换0到15之间的数字。
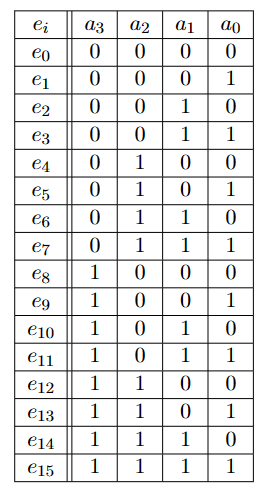
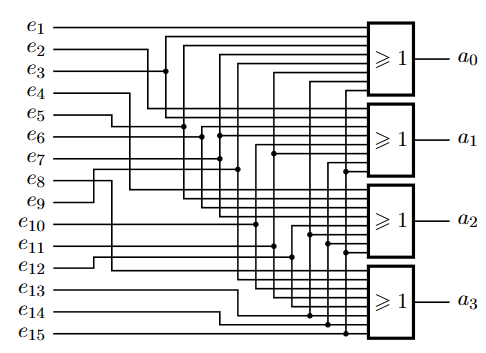
由此,我们可以将四位输出写作:
\[ \left\{\begin{array}{l}a_0=e_1+e_3+e_5+e_7+e_9+e_{11}+e_{13}+e_{15} \\a_1=e_2+e_3+e_6+e_7+e_{10}+e_{11}+e_{14}+e_{15} \\a_2=e_4+e_5+e_6+e_7+e_{12}+e_{13}+e_{14}+e_{15} \\a_3=e_8+e_9+e_{10}+e_{11}+e_{12}+e_{13}+e_{14}+e_{15}\end{array}\right. \]
解码器 décodeur
解码器可以对机器的信息处理结果进行解码。它是一个数字/模拟转换器(或DAC)
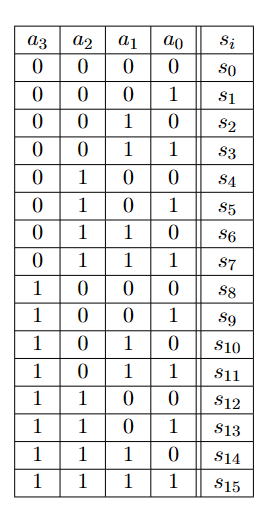

可以得到:
\[ \begin{array}{ll}s_0=\overline{a_0} \cdot \overline{a_1} \cdot \overline{a_2} \cdot \overline{a_3} & s_8=\overline{a_0} \cdot \overline{a_1} \cdot \overline{a_2} \cdot a_3 \\s_1=a_0 \cdot \overline{a_1} \cdot \overline{a_2} \cdot \overline{a_3} & s_9=a_0 \cdot \overline{a_1} \cdot \overline{a_2} \cdot a_3 \\s_2=\overline{a_0} \cdot a_1 \cdot \overline{a_2} \cdot \overline{a_3} & s_{10}=\overline{a_0} \cdot a_1 \cdot \overline{a_2} \cdot a_3 \\s_3=a_0 \cdot a_1 \cdot \overline{a_2} \cdot \overline{a_3} & s_{11}=\overline{a_0} \cdot a_1 \cdot \overline{a_2} \cdot a_3 \\s_4=\overline{a_0} \cdot \overline{a_1} \cdot a_2 \cdot \overline{a_3} & s_{12}=\overline{a_0} \cdot \overline{a_1} \cdot a_2 \cdot a_3 \\s_5=a_0 \cdot \overline{a_1} \cdot a_2 \cdot \overline{a_3} & s_{13}=a_0 \cdot \overline{a_1} \cdot a_2 \cdot a_3 \\s_6=\overline{a_0} \cdot a_1 \cdot a_2 \cdot \overline{a_3} & s_{14}=\overline{a_0} \cdot a_1 \cdot a_2 \cdot a_3 \\s_7=a_0 \cdot a_1 \cdot a_2 \cdot \overline{a_3} & s_{15}=a_0 \cdot a_1 \cdot a_2 \cdot a_3\end{array} \]
多路复用器 Multiplexeurs
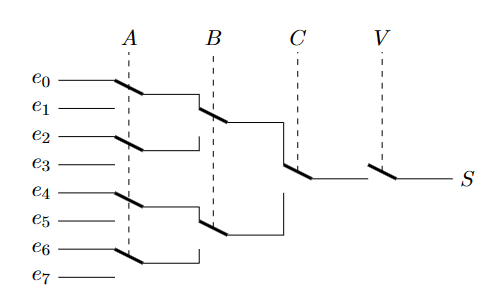
多路复用器是将来自 2n 个串联通道的并行信号组合到单个通道上。因此,功能框显示 2n 个数据输入、n 个选择(或地址)输入、一个验证输入和一个输出
\[ \begin{aligned} S= & \left(\bar{A} \cdot \bar{B} \cdot \bar{C} \cdot e_0+A \cdot \bar{B} \cdot \bar{C} \cdot e_1+\bar{A} \cdot B \cdot \bar{C} \cdot e_2+A \cdot B \cdot \bar{C} \cdot e_3\right. \\ & \left.+\bar{A} \cdot \bar{B} \cdot C \cdot e_4+A \cdot \bar{B} \cdot C \cdot e_5+\bar{A} \cdot B \cdot C \cdot e_6+A \cdot B \cdot C \cdot e_7\right) \cdot V \end{aligned} \]
多路复用器可用于两种操作模式:
- 作为数据选择器:多路复用器在其数据输入上接收可变信号,并通过其地址输入进行控制。那么,多路复用本身包括改变地址输入组合的值,以便在输出处连续感知注入数据输入的每个信号。
- 作为逻辑综合工具:多路复用器在其地址输入上接收可变信号,并通过其数据输入进行控制。在这种情况下,多路复用器用于从其地址输入执行逻辑功能,该逻辑功能在输出处注入。
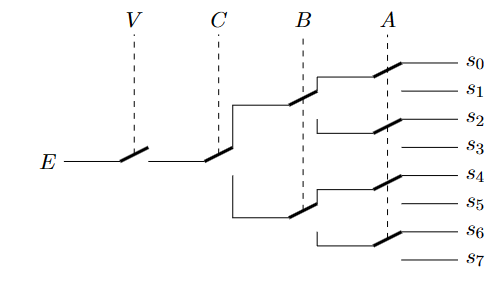
多路解复用器
解复用器是在 2n 个通道之一上发送数据输入。因此,功能框显示一个数据输入、n 个选择(或地址)输入、一个验证输入和 2n 个输出。
\[ \left\{\begin{array}{l}s_0=\bar{A} \cdot \bar{B} \cdot \bar{C} \cdot V \cdot E \\s_1=A \cdot \bar{B} \cdot \bar{C} \cdot V \cdot E \\s_2=\bar{A} \cdot B \cdot \bar{C} \cdot V \cdot E \\s_3=A \cdot B \cdot \bar{C} \cdot V \cdot E \\s_4=\bar{A} \cdot \bar{B} \cdot C \cdot V \cdot E \\s_5=A \cdot \bar{B} \cdot C \cdot V \cdot E \\s_6=\bar{A} \cdot B \cdot C \cdot V \cdot E \\s_7=A \cdot B \cdot C \cdot V \cdot E\end{array}\right. \]