算符作用在左矢和右矢上 Action des opérateurs sur les kets et les bras
算符作用在左矢和右矢上 Action des opérateurs sur les kets et les bras
投影算符和闭合关系 Projecteurs et relation de fermeture
引→二维希尔伯特空间的例子

在二维空间中,这两个向量是组成基的两个向量,这个问题相当于:
\[ \left(\begin{array}{l}1 \\0\end{array}\right)\left(\begin{array}{ll}1 & 0\end{array}\right)+\left(\begin{array}{l} 0 \\ 1 \end{array}\right)\left(\begin{array}{ll} 0 & 1 \end{array}\right) = \left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right) \]
投影算符 Projecteurs
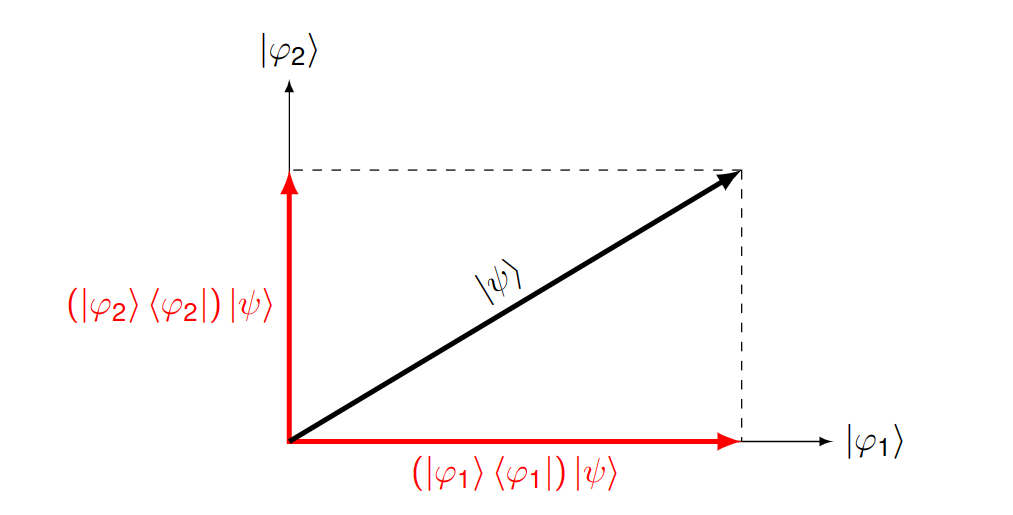
以一个二维空间为例,向两个基向量的投影如下,可以参考引→二维希尔伯特空间的例子
\[ \begin{aligned}& P_{\varphi_1}=\left|\varphi_1\right\rangle\left\langle\varphi_1\right|: \text { projecteur sur }\left|\varphi_1\right\rangle \\& P_{\varphi_2}=\left|\varphi_2\right\rangle\left\langle\varphi_2\right|: \text { projecteur sur }\left|\varphi_2\right\rangle\end{aligned} \]
- 投影算符的性质:
- \(P_{\varphi_1}^2=P_{\varphi_1}, P_{\varphi_2}^2=P_{\varphi_2}\)
闭合关系 Relation de fermeture
- \(\sum_n\left|\varphi_n\right\rangle\left\langle\varphi_n\right|=\widehat{\mathbb{1}}\)
算符的矩阵表示 Représentation matricielle d’un opérateur
非简并的算符的矩阵表示
一个非简并的算符满足:
\[ \widehat{A}\left|\varphi_n\right\rangle=a_n\left|\varphi_n\right\rangle \]
故其矩阵可以表示为:
\[ \ widehat{A}=\left(\begin{array}{cccc}a_1 & 0 & \cdots & 0 \\0 & a_2 & \cdots & 0 \\\vdots & \vdots & \ddots & \vdots \\0 & 0 & \cdots & a_n\end{array}\right) = \left(\begin{array}{cccc} \left\langle\varphi_1|\widehat{A}| \varphi_1\right\rangle & 0 & \cdots & 0 \\ 0 & \left\langle\varphi_2|\widehat{A}| \varphi_2\right\rangle & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \left\langle\varphi_n|\widehat{\widehat{A}}| \varphi_n\right\rangle \end{array}\right) \]
注意关系:\(\left\langle\varphi_m|\widehat{A}| \varphi_n\right\rangle=a_n\left\langle\varphi_m \mid \varphi_n\right\rangle=a_n \delta_{m n}\)
简并的算符的矩阵表示
非简并的算符满足:
\[ \widehat{B}\left|\varphi_n\right\rangle=\sum_m b_{m, n}\left|\varphi_m\right\rangle \]
考察左侧表达式:
\[ \begin{aligned} \widehat{B}|\psi\rangle & =\widehat{B} \widehat{\mathbb{1}}|\psi\rangle =\widehat{B}\left(\sum_n\left|\varphi_n\right\rangle\left\langle\varphi_n\right|\right)|\psi\rangle \\ & =\left(\sum_n \widehat{B}\left|\varphi_n\right\rangle\left\langle\varphi_n\right|\right)|\psi\rangle =\left(\sum_{m, n} b_{m, n}\left|\varphi_m\right\rangle\left\langle\varphi_n\right|\right)|\psi\rangle \end{aligned} \]
从而得到:
\[ \widehat{B}=\sum_{m, n} b_{m, n}\left|\varphi_m\right\rangle\left\langle\varphi_n\right| \]
其矩阵表示为:
\[ \widehat{B}=\left(\begin{array}{cccc} \left\langle\varphi_1|\widehat{B}| \varphi_1\right\rangle & \left\langle\varphi_1|\widehat{B}| \varphi_2\right\rangle & \cdots & \left\langle\varphi_1|\widehat{B}| \varphi_n\right\rangle \\ \left\langle\varphi_2|\widehat{B}| \varphi_1\right\rangle & \left\langle\varphi_2|\widehat{B}| \varphi_2\right\rangle & \cdots & \left\langle\varphi_2|\widehat{B}| \varphi_n\right\rangle \\ \vdots & \vdots & \ddots & \vdots \\ \left\langle\varphi_n|\widehat{B}| \varphi_1\right\rangle & \left\langle\varphi_n|\widehat{B}| \varphi_2\right\rangle & \cdots & \left\langle\varphi_n|\widehat{B}| \varphi_n\right\rangle \end{array}\right) \]
算符的对易关系
算符的不可对易性
\[ \begin{aligned}\widehat{B} \widehat{A}|\psi\rangle & =\left(\sum_{m, n} b_{m, n}\left|\varphi_m\right\rangle\left\langle\varphi_n\right|\right)\left(\sum_{p, q} a_{p, q}\left|\varphi_p\right\rangle\left\langle\varphi_q\right|\right)|\psi\rangle \\& =\left[\sum_{m, q}\left(\sum_n b_{m, n} a_{n, q}\right)\left|\varphi_m\right\rangle\left\langle\varphi_q\right|\right]|\psi\rangle \\\widehat{A} \widehat{B}|\psi\rangle & =\left[\sum_{m, q}\left(\sum_n a_{m, n} b_{n, q}\right)\left|\varphi_m\right\rangle\left\langle\varphi_q\right|\right]|\psi\rangle\end{aligned} \]
故:
\[ \sum_n a_{m, n} b_{n, q} \neq \sum_n b_{m, n} a_{n, q} \Rightarrow \widehat{A} \widehat{B}|\psi\rangle \neq \widehat{B} \widehat{A}|\psi\rangle \]
所以量子力学中的算符一般来说是不可对易的。
对易子 Commutateurs
量子算符的对易子被定义为:
\[ [\widehat{A}, \widehat{B}] \triangleq \widehat{A} \widehat{B}-\widehat{B} \widehat{A} \]
如果满足\([\widehat{A}, \widehat{B}]=0\),则两个算符是可对易的(可交换的)。
对易子的计算
对易子计算中非常重要的性质,展开即可证明:l
\[ \begin{align}&[\widehat{A}, \widehat{B} \widehat{C}]=\widehat{B}[\widehat{A}, \widehat{C}]+[\widehat{A}, \widehat{B}] \widehat{C},\\& [\widehat{A} \widehat{B}, \widehat{C}]=\widehat{A}[\widehat{B}, \widehat{C}]+[\widehat{A}, \widehat{C}] \widehat{B}\end{align} \]
对易子的应用
- 在本章中,与对易子相关的最重要的性质即为,会在本章的结尾部分加以证明:
\[ \begin{align}\left[\widehat{x}, \widehat{p}_x\right]=i \hbar \widehat{\mathbb{1}} \Rightarrow \Delta_\psi x \Delta_\psi p_x \geqslant \frac{\hbar}{2}\end{align} \]
共同可对易的可观测量的完全集合 E.C.O.C.
E.C.O.C 定义
\(\widehat{A}, \widehat{B}, \widehat{C} , \widehat{D}\)可对易的一组可观测量
态\(\left|\phi_i\right\rangle\)可以被写成者这组可观测量的共同本征体(同时对角化的感觉):
\[ \begin{aligned}A\left|\phi_i\right\rangle & =a_i\left|\phi_i\right\rangle, \\B\left|\phi_i\right\rangle & =b_i\left|\phi_i\right\rangle, \\C\left|\phi_i\right\rangle & =c_i\left|\phi_i\right\rangle, \\D\left|\phi_i\right\rangle & =d_i\left|\phi_i\right\rangle,\end{aligned} \]
那么态\(\left|\phi_i\right\rangle\)就是这组可观测量的共同本征态,如果在这个观察下\(\left|\phi_i\right\rangle=\left|a_i, b_i, c_i, d_i\right\rangle\),则称\(\widehat{A}, \widehat{B}, \widehat{C} , \widehat{D}\)组成了共同可对易的可观测量的完全集合
势阱的例子
一维势阱
能量的本征值为:
\[ \varepsilon_i=\frac{n_i^2 \pi^2 \hbar^2}{2 m a^2} \]
对应的能量本征态:\(\left|\varphi_i\right\rangle=\left|\varepsilon_i\right\rangle=\left|n_i\right\rangle\),\(\left|n_i\right\rangle\)表示例子在第\(n_i\)个能级上的波函数。在这种情况下,这些所有的本征态都可以用一个整数\(n_i\)来表示。这个整数构成了ECOC。
二维势阱
能量的本征值为:
\[ \varepsilon_i=\frac{\left(n_x^2+n_y^2\right) \pi^2 \hbar^2}{2 m a^2} \]
其中\(n_x\)和\(n_y\)分别是沿着两个坐标轴的量子数。
这是,能量本征态可以表示为\(\left|\varphi_i\right\rangle=\left|n_x, n_y\right\rangle=\left|\varepsilon_i, n_y\right\rangle\)。无论使用哪种表示,这些态都构成了ECOC。
期望和方差 Valeur moyenne et incertitude
期望 Valeur moyenne
我们使用期望来计算本征态的平均值:\(\langle A\rangle_\psi=\sum_n p_n a_n\)
将概率分解为态向本征态的投影的平方:\(p_n=\left|\left\langle\varphi_n \mid \psi\right\rangle\right|^2 = \left\langle\psi \mid \varphi_n\right\rangle\left\langle\varphi_n \mid \psi\right\rangle\)
引入算符表示:\(\langle A\rangle_\psi=\sum_n\left\langle\psi\left|a_n\right| \varphi_n\right\rangle\left\langle\varphi_n \mid \psi\right\rangle =\langle A\rangle_\psi=\sum_n\left\langle\psi|\widehat{A}| \varphi_n\right\rangle\left\langle\varphi_n \mid \psi\right\rangle\)
合并求和:\(\langle A\rangle_\psi=\left\langle\psi\left|\widehat{A}\left(\sum_n\left|\varphi_n\right\rangle\left\langle\varphi_n\right|\right)\right| \psi\right\rangle\)
得到期望:
\[ \begin{align}\langle A\rangle_\psi=\langle\psi|\widehat{A}| \psi\rangle\end{align} \]
平均标准差 Écart quadratique moyen (incertitude)
平均标准差被定义为:
\[ \Delta_\psi(A)=\sqrt{\left\langle\left(\widehat{A}-\langle A\rangle_\psi\right)^2\right\rangle_\psi} \]
可进一步化简为:
\[ \begin{align}\Delta_\psi(A)=\sqrt{\left\langle A^2\right\rangle_\psi-\langle A\rangle_\psi^2}\end{align} \]
与期望和方差相关的一个例子
广义海森堡不确定性关系 Relation d’incertitude de Heisenberg généralisée
假设\([\widehat{A}, \widehat{B}]=i \hbar \widehat{C}\),构建:
\[ \left(\widehat{A}-\langle A\rangle_\psi\right)+i \lambda\left(\widehat{B}-\langle B\rangle_\psi\right), \lambda \in \mathbb{R} \]
应有:
\[ \|\left[\left(\widehat{A}-\langle A\rangle_\psi\right)+i \lambda\left(\widehat{B}-\langle B\rangle_\psi\right)\right]|\psi\rangle \|^2 \geqslant 0 \]
从而使得有效值:
\[ \left\langle\psi\left|\left(\widehat{A}-\langle A\rangle_\psi\right)^2+\lambda^2\left(\widehat{B}-\langle B\rangle_\psi\right)^2+i \lambda[\widehat{A}, \widehat{B}]\right| \psi\right\rangle \geqslant 0 \]
带入C:
\[ \left\langle\left(\widehat{A}-\langle A\rangle_\psi\right)^2\right\rangle_\psi+\lambda^2\left\langle\left(\widehat{B}-\langle B\rangle_\psi\right)^2\right\rangle_\psi-\lambda \hbar\langle C\rangle_\psi \geqslant 0 \]
从而最终得到:
\[ \hbar^2\langle C\rangle_\psi^2-4\left\langle\left(\widehat{A}-\langle A\rangle_\psi\right)^2\right\rangle_\psi\left\langle\left(\widehat{B}-\langle B\rangle_\psi\right)^2\right\rangle_\psi \leqslant 0 \]
或者写作:
\[ \begin{align}\Delta_\psi(A) \Delta_\psi(B) \geqslant \frac{\hbar}{2}\langle C\rangle_\psi \ ,\ [\widehat{A}, \widehat{B}]=i \hbar \widehat{C}\end{align} \]
连续基和波函数
连续波函数的表示
\[ |\psi\rangle=\sum_n\left\langle\varphi_n \mid \psi\right\rangle\left|\varphi_n\right\rangle \Rightarrow|\psi\rangle=\int\langle x \mid \psi\rangle|x\rangle \mathrm{d} x \]
连续概率的表示
\[ p_n=\left|\left\langle\varphi_n \mid \psi\right\rangle\right|^2 \Rightarrow p(x)=|\langle x \mid \psi\rangle|^2=|\psi(x)|^2 \]
闭合原理
即总概率为1
\[ \int|x\rangle\langle x| \mathrm{d} x=\widehat{\mathbb{1}} \]
位置表示和动量表示
- \(\langle x \mid \psi\rangle=\psi(x)\)
- \(\left\langle p_x \mid \psi\right\rangle=\bar{\psi}\left(p_x\right)\)
位置和动量之间的转换
\[ \psi(\vec{r})=\frac{1}{(2 \pi \hbar)^{3 / 2}} \int e^{i \vec{p} \cdot \vec{r} / \hbar} \bar{\psi}(\vec{p}) d^3 p \]
位置和动量的不确定度
\[ \begin{aligned}{\left[\widehat{x}, \widehat{p}_x\right] \psi(x) } & =\left(\widehat{x} \widehat{p}_x-\widehat{p}_x \widehat{x}\right) \psi(x)=x \frac{\hbar}{i} \frac{\partial}{\partial x} \psi(x)-\frac{\hbar}{i} \frac{\partial}{\partial x}(x \psi(x)) \\& =i \hbar \psi(x)\end{aligned} \]
\[ \left[\widehat{x}, \widehat{p}_x\right]=i \hbar \widehat{\mathbb{1}} \Rightarrow \Delta_\psi x \Delta_\psi p_x \geqslant \frac{\hbar}{2} \]



