CRS II 结构模态计算 Calcul modal des structures

振动的模态 Modes de vibration

振动的概念 Notion de mode

单一方向牵引压缩震动的例子

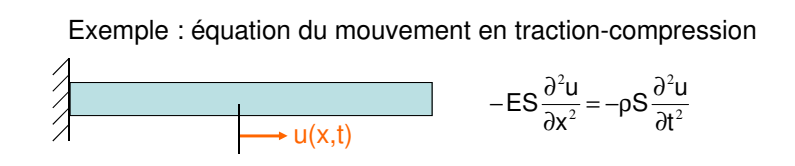
根据达朗贝尔原理，其解符合：

\[ u(x, t)=f(x-c t)+g(x+c t) \]

如果我们分离变量，将u分解为：\(\mathrm{u}(\mathrm{x}, \mathrm{t})=\mathrm{U} \cdot \mathrm{X}(\mathrm{x}) \cdot \mathrm{T}(\mathrm{t})\)，传播方程可以被写作：

\[ \frac{1}{X} \frac{d^2 X}{d x^2}=\frac{1}{T} \frac{d^2 T}{d t^2} \frac{\rho S}{E S}=-k^2 \]

由此可以分别求解两个部分：

• 空间简谐解：

  \[ \begin{aligned}X & =A_{+} e^{+i k x}+A_{-} e^{-i k x} \\& =A_C \cos (k x)+A_S \sin (k x)\end{aligned} \]

• 时间简谐解：

  \[ \begin{aligned} T & =B_{+} e^{+i \omega t}+B_{-} e^{-i \omega t} \\ & =B_C \cos (\omega t)+B_S \sin (\omega t) \end{aligned} \]

  其中，

  \[ \omega^2=\frac{E I}{\rho S} k^2 \]

由\(u(x, t)=U \cdot X(x) \cdot T(t) \equiv f(x-c t)+g(x+c t)\)，得到色散关系：

\[ c=\frac{\omega}{k} \]

模态的定义 Définition des modes

🌉 振动问题的齐次方程有简谐解。这些解对应于驻波。

本征模态被定义为齐次方程的自由简谐解，在当前问题下，齐次意味着不受任何的外力影响：

\[ \mathrm{u}(\mathrm{x}, \mathrm{t}) \quad \mapsto \quad \mathrm{u}(\mathrm{x}, \mathrm{t})=\phi(\mathrm{x}) \mathrm{e}^{\mathrm{i} \omega t} \]

由此，强表述的方程可以被写作：

\[ A u=-\rho \ddot{u} \Rightarrow A \phi=\rho \omega^2 \phi \]

弱表述的运动方程可以等价地以积分形式写出，只需要将强表述的方程两边乘以一个函数v并在整个域上积分：

\[ \int_{\Omega} \text { Auv } \mathrm{d} \Omega=-\int_{\Omega} \rho \ddot{u} v \mathrm{d} \Omega \quad \Rightarrow [\cdots]_{\partial \Omega}+\mathrm{a}(\mathrm{u}, \mathrm{v})=-\int_{\Omega} \rho \ddot{u} . \mathrm{d} \Omega \quad \forall \mathrm{v} \]

在齐次条件下，我们认为方程的第一项代表的非齐次部分等于0，并将等式右侧的部分记为：

\[ (\rho \ddot u, v) = -\int_{\Omega} \rho \ddot{u} \cdot \mathrm{d} \Omega \]

得到一个两端都是二次型的方程：

\[ \mathrm{a}(\mathrm{u}, \mathrm{v})=(\rho \mathrm{u}, \mathrm{v}) \quad \forall \mathrm{v} \]

由此，两种表述分别为：

\[ \left\{\begin{aligned}&Au = -\rho\ddot{u}\\&a(u,v) = (\rho\ddot{u},v)\end{aligned}\right. \]

在简谐假设之后，两个方程可以写作：

\[ \left\{\begin{aligned}&Au = \rho \omega^2u\\&a(u,v) = \omega^2(\rho u,v)\end{aligned}\right. \]

或者也可以写作：

\[ \left\{\begin{aligned}&Ax = k^2x\\&a(x_n,x_p) = k^2( x_n,x_p)\end{aligned}\right. \]

我们所要做的目标，即利用运动方程的弱形式来得到定义在解向量空间上的对称线性形式。接下来我们会用两个例子证明两种表述的等价。

张力压缩杆的例子 Barre en traction-compression

对于Barre en traction-compression， 其运动方程：

\[ -\frac{\partial}{\partial x}\left(E S \frac{\partial u}{\partial x}\right)=-\rho S \frac{\partial^2 u}{\partial t^2} \]

根据方程：\(A u=-\rho \ddot{u}\)，可将其简化为：

\[ A u=-\frac{\partial}{\partial x}\left(E S \frac{\partial u}{\partial x}\right) \]

然后我们考察\((A u, v)\)，为了使其对称，我们应用分步积分：

\[ (A u, v)=\int_0^L A u \cdot v d x=-\int_0^L \frac{\partial}{\partial x}\left(E S \frac{\partial u}{\partial x}\right) \cdot v d x=-\left[E S \frac{\partial u}{\partial x} \cdot v\right]_0^L+\int_0^L E S \frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} d x \]

在没有外力的情况下（齐次情况下），第一项为0，得到：

\[ a(u, v)=\int_0^L E S \frac{\partial u}{\partial x} \cdot \frac{\partial v}{\partial x} d x \]

此外：

\[ (\rho \ddot{u}, v)=-\int_0^L S \rho \ddot u . v d x \]

弯梁的例子 Poutre en flexion

弯梁的动力学方程

\[ \frac{\partial^2}{\partial x^2}\left(E I \frac{\partial^2 u}{\partial x^2}\right)=-\rho S \frac{\partial^2 u}{\partial t^2} \]

得到Au的表述：

\[ A u=\frac{\partial^2}{\partial x^2}\left(E I \frac{\partial^2 u}{\partial x^2}\right) \]

同时有：

\[ (\rho \ddot{u}, v)=-\int_0^L S \rho \ddot{u} . v d x \]

考察（Au,v），得：

\[ (A u, v)=\int_0^L \frac{\partial^2}{\partial x^2}\left(E I \frac{\partial^2 u}{\partial x^2}\right) \cdot v d x=\left[\frac{\partial}{\partial x}\left(E I \frac{\partial^2 u}{\partial x^2}\right) v\right]_0^L-\left[E I \frac{\partial^2 u}{\partial x^2} \frac{\partial v}{\partial x}\right]_0^L+\int_0^L E I \frac{\partial^2 u}{\partial x^2} \cdot \frac{\partial^2 v}{\partial x^2} d x \]

前两项都为0，得到：

\[ a(u, v)=\int_0^L E I \frac{\partial^2 u}{\partial x^2} \cdot \frac{\partial^2 v}{\partial x^2} d x \]

模态

对于任意一个自由简谐解\(\phi_{\mathrm{i}}\)，存在\(\omega_i\)使得：

\[ \underset{\text { + cdts. limites }}{A \phi_{\mathrm{i}}=\rho \omega_{\mathrm{i}}^2 \phi_{\mathrm{i}}} \quad \Leftrightarrow \quad \mathrm{a}\left(\phi_{\mathrm{i}}, \mathrm{v}\right)=\omega_{\mathrm{i}}^2\left(\rho \phi_{\mathrm{i}}, \mathrm{v}\right) \quad \forall \mathrm{v} \]

\(\left(\phi_i, \omega_i\right)\)被称为第\(i\)的模态。

模态的性质

正交性 Orthogonalité des modes propres

对于模态\(\begin{aligned}& \left(\omega_n, \phi_n\right) ， \left(\omega_p, \phi_p\right)\end{aligned}\)，有：

\[ \begin{aligned}& \mathrm{a}\left(\phi_n, \phi_p\right)=\omega_n^2\left(\rho \phi_n, \phi_p\right) \\& \mathrm{a}\left(\phi_p, \phi_n\right)=\omega_p^2\left(\rho \phi_p, \phi_n\right)\end{aligned} \]

从而得到：

\[ \left(\omega_n^2-\omega_p^2\right)\left(\rho \phi_p, \phi_n\right)=0 \]

从而得到正交性：

\[ \left(\rho \phi_p, \phi_n\right)=0 \]

独特和归一化

假设\(\left(\omega_n, \phi_n\right)\)模态，根据定义，有：

\[ A \phi_n=\rho \omega_n^2 \phi_n\Rightarrow A \alpha \phi_n=\rho \omega_n^2 \alpha \phi_n \]

从而得到\(\alpha\phi_n\)也是一个模态。因此，我们只选择归一化为1的模态。

\[ \left(\rho \phi_n, \phi_n\right)=1 \]

正交归一化的基

由此，模态是一个空间的正交归一化的基，因此有：

\[ u(x, t)=\sum_n \lambda_n(t) \cdot \phi_n(x) \]

模态基

我们可以将所有的通解表示为：

\[ u(x, t)=\sum_i q_i(t) \cdot \phi_i(x) \]

求解非齐次方程

在获得通解之后，我们试图求出特解：

对于强表述：

\[ A u=-\rho \ddot{u}+f \text { et cdts. limites } \]

对应的弱表述方程：

\[ \int_{\Omega} \text { Au. } \phi_j d x+\int_{\Omega} \rho \ddot{u} \cdot \phi_j d x=\int_{\Omega} f \cdot \phi_j d x \quad \forall \phi_j \]

代入通解：

\[ \int_{\Omega} A \sum_i q_i(t) \cdot \phi_i(x) \cdot \phi_j d x+\int_{\Omega} \rho \sum_i \ddot{q}_i(t) \cdot \phi_i(x) \cdot \phi_j d x=\int_{\Omega} f \cdot \phi_j d x \quad \forall \phi_j \]

替换第一项，并对第二项应用分步积分可以得到：

\[ \sum_i q_i(t) \cdot a\left(\phi_i, \phi_j\right)-\int_{\partial \Omega}\left(H \sum_i q_i \cdot \phi_i\right) \cdot \phi_j d x+\ddot{q}_j=f_j \]

其中\(H\)是边界微分算符，整个第二项可以写作\(F_j\)，代表作用在边界上的力。

根据正交化特点，第一项只有在\(i = j\)时非零：

\[ \sum_i q_i(t) \cdot a\left(\phi_i, \phi_j\right) = \omega_j^2 q_j \]

由此可以得到方程：

\[ \ddot{q}_j+\omega_j^2 q_j=F_j+f_j \]

简谐响应

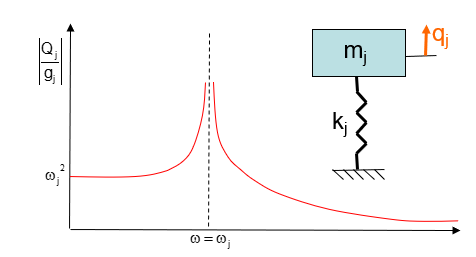
假设外力为简谐力，即\(F_j+f_j=g_j e^{i \omega t}\)，那么解一定符合：

\[ q_j=Q_j e^{i \omega t}+\text { 平移项 } \]

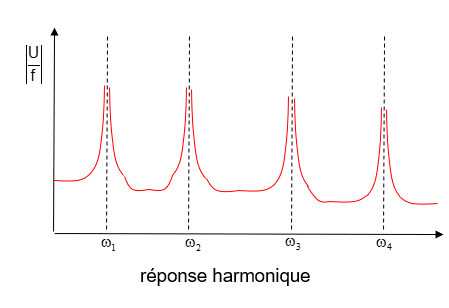
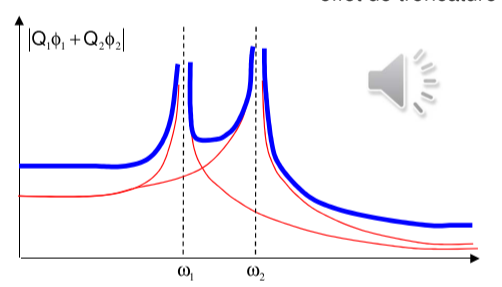
截断效应

为了简化计算，我们只取模态分析中的前N个模态来近似整个系统的响应。

\[ \begin{aligned}& u(x, t)=\sum_{i=1}^{\infty} q_i(t) \cdot \phi_i(x) \\& \tilde{u}(x, t)=\sum_{i=1}^N q_i(t) \cdot \phi_i(x)\end{aligned} \]

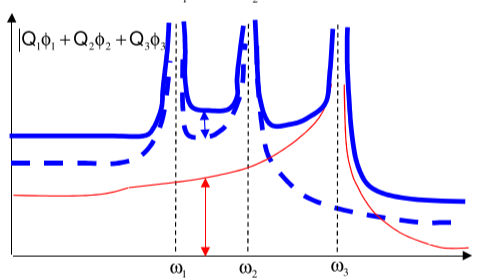
阻尼

振动方程与阻尼

阻尼效应在共振时限制了系统响应的幅度。在结构动力学中，阻尼是非常重要的因素，因为它影响着结构在动态载荷作用下的响应。给出的振动方程：

\[ \ddot{\mathrm{q}}_{\mathrm{j}}+2 \xi_j \omega_j \dot{\mathrm{q}}_j+\omega_j^2 \mathrm{q}_j=\mathrm{F}_{\mathrm{j}}+\mathrm{f}_{\mathrm{j}} \]

\(\xi_j=\frac{c_j}{2 m_j \omega_j}\)是阻尼率，其中\(\mathrm{c}_{\mathrm{j}}\)是阻尼参数。

Basile 假设

Basile 假设认为每个模态都有自己的阻尼，并且模态之间没有耦合。这意味着一个模态的阻尼不会影响其他模态。这个假设通常用于简化复杂系统的分析。

能量耗散潜能

“能量耗散潜能”是一个描述系统中由于粘性力或其他阻尼机制而耗散能量的方式的函数。在这个假设下，模态的正交性得以保持，即使在有阻尼的情况下，各个模态仍然保持独立。

拉伸，弯曲的模态分析

拉伸压缩杆的例子

将\(u(x,t)\)替换为简谐驻波解

由上一章内容，已知运动问题和边界条件：

\[ \begin{align} &\rho S \ddot{u}-E S \frac{\partial^2 u(x, t)}{\partial x^2} = 0 \\ & \left\{ \begin{aligned} &u(0,t) = 0 \\ &E S \frac{\partial u(L, t)}{\partial x}=M\frac{\partial^2 u(L, t)}{\partial x^2} \end{aligned} \right. \end{align} \]

假设\(u=U X(x) \cdot T(t)\)，其中\(\ddot T(t) = -\omega^2T(t)\)，代入上述三个方程：

$$ \[\begin{align} &\rho S \omega^2X(x)+E S \frac{d^2 X(x, t)}{dx^2} = 0 \\ & \left\{ \begin{aligned} &X(0) = 0 \\ &E S \frac{\partial X(L)}{\partial x}=M\omega^2X(L) \end{aligned} \right. \end{align}\] $$

进行一定的变量替换，设\(\mu=\frac{M}{\rho S L}\)和\(k^2=\frac{\rho S}{E S} \omega^2\)，得到运动方程和边界条件：

$$ \[\begin{align} &\frac{d^2 X(x, t)}{dx^2}+k^2X(x) = 0 \\ & \left\{ \begin{aligned} &X(0) = 0 \\ & \frac{\partial X(L)}{\partial x}=\mu k^2 L X(L) \end{aligned} \right. \end{align}\] $$

求解

• 微分方程\((5)\)的一般解为：

  \[ X(x) = Acos(kx)+Bsin(kx) \]

• 由第一个边界条件，有：

  \[ X(0) = 0\Rightarrow A = 0 \]

  得到：

  \[ X(x) = Bsin(kx) \]

• 考虑第二个边界条件：

\[ B k \cos (k L)-\mu k^2 L B \sin (k L)=0\Rightarrow\tan (k L)=\frac{1}{\mu k L} \]

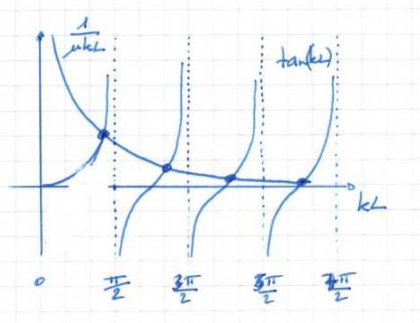
• 分析\(\mu = 0\)的情况，有\(tan(kL) = \infty\)，得到：

\[ kL = \frac \pi 2 +n\pi\Rightarrow k_n = \frac{(2n+1)\pi}{2L}\Rightarrow\omega_n = \sqrt{\frac E \rho}\frac{(2n-1)\pi}{2L} \]

• 分析\(\mu = \infty\)的情况，有\(tan(kL) = 0\)，得到：

  \[ kL = n\pi\Rightarrow k = \frac{n\pi}{L}\Rightarrow \omega_n=\sqrt{\frac{E}{\rho}} \frac{n \pi}{L} \]

  然而值得注意的是，\(X_n(x) = B_nsin(k_nx) = 0\)，所以在\(\mu = \infty\)的情况下，有段相z当于被约束。

模态分析和正交性

我们已知强表述的形式：

\[ x_n^{\prime \prime}+k_n^2 x_n=0 \]

对其乘以\(x_p\)，然后积分得：

\[ \begin{align}& \int_0^L\left(x_n^{\prime \prime}+k_n^2 x_n\right) x_p d x=0 \nonumber\\& \int_0^L x_n^{\prime \prime} x_p d x+k_n^2 \int_0^L x_n x_p d x=0\end{align} \]

\((7)\)式的第二项为双线型，但第一项不是双线型，为了使\(x_n,x_p\)齐次，应用分部积分：

\[ \left[x_n^{\prime} x_p\right]_0^L-\int_0^L x_n^{\prime} x_p^{\prime} d x+k_n^2 \int_0^L x_n x_p d n=0 \]

得到两个双线型的和的形式：

\[ \begin{align}-\int_0^L x_n^{\prime} x_p^{\prime} d x+k_n^2\left[\mu L x_n(L) x_p(L)+\int_0^L x_n x_p d x\right]=0\end{align} \]

假设：

\[ \begin{aligned} & a\left(x_n, x_p\right)=\int_0^L x_n^{\prime} x_p^{\prime} d n \\ & \left(x_n, x_p\right)=\mu L x_n(L) x_p(L)+\int_0^L x_n x_p d r \end{aligned} \]

代入\((8)\)得：

\[ \begin{align}-a\left(x_n, x_p\right)+k_n^2\left(x_n, x_p\right)=0\end{align} \]

同理有：

\[ \begin{align}-a\left(x_p, x_n\right)+k_p^2\left(x_p, x_n\right)=0\end{align} \]

根据对称性，\((10)-(9)\)得：

\[ 0 +\left(k_n^2-k_p^2\right)\left(x_p, x_n\right)=0\Rightarrow \left(x_p, x_n\right)=0 \]

可见正交性 orthogonalité。

受力的情况

\[ -E S v^{(2)}+\rho S \ddot{v}=F \delta _{x=L / 2} \]

使用模态基形式代换：

\[ -E S \sum q_n X_n^{(2)}+\rho S \sum \ddot{q_n}X_n=F \delta _{x=L } \]

应用变换\(\int_0^L x_i(\ldots) d x\)得到：

\[ \ddot{q}_n+\omega_n^2 q_n=F_0 x_n(L) e^{i \omega t} \]

可以求得：

\[ q_n=\frac{F_0 x_n(L)}{\omega_n^2-\omega^2} e^{i \omega t} \]

因此：

\[ u(x, t)=\sum_{n=1}^{\infty} \frac{F_0 X_n(L) X_n(x)}{\omega_n^2-\omega^2} e^{i a t} \]

对于静态反馈：\(\omega = 0\)：

$$ u(x, t)=_{n=1}^{}

=

$$

对于动态反馈，应用截断效应：

\[ \begin{aligned} U(x, t) & =\sum_{n=1}^N \frac{F_0 X_n(L) X_n(x)}{\omega_n^2-\omega^2} e^{i \omega t}+\sum_{n+N+1}^{\infty} \frac{F_0 X_n(L) X_n(x)}{\omega_n^2-\omega^2} e^{i \omega t} \\ & \simeq \sum_{n=1}^N \frac{F_0 X_n(L) X_n(x)}{\omega_n^2-\omega^2} e^{i \omega t}+\sum_{n=N+1}^{\infty} \frac{F_0 X_n(L) X_n(x)}{\omega_n^2} e^{i \omega t} \\& =\sum_{n=1}^N \frac{F_0 X_n(L) X_n(x)}{\omega_n^2-\omega^2} e^{i \omega t}+\left(\frac{F_0 x}{E J}-\sum_{n=1}^N \frac{F_0 X_n(L) x_n(x)}{\omega_n^2}\right) e^{i \omega t} \end{aligned} \]

弯梁的例子

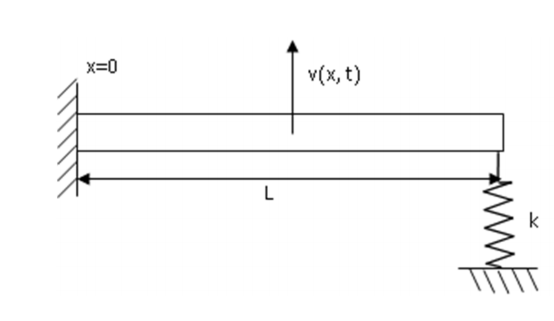
根据上一张，有运动方程和约束条件：

\[ \begin{align}& \frac{\partial^2}{\partial x^2}\left(E I \frac{\partial^2 v}{\partial x^2}\right)=-\rho S \frac{\partial^2 v}{\partial t^2} \\& \left\{\begin{aligned} &v(0, t)=0 \\ &\frac{\partial^2 v(L, t)}{\partial x^2}=0 \\& \frac{\partial v(0, t)}{\partial x}=0 \\& E I \frac{\partial^3 v(L, t)}{\partial x^3}=K \cdot v(L, t) \end{aligned}\right. \end{align} \]

求简谐解

设\(v(x, t)=X(x) \cdot e^{i \omega t}\)，代入公式\((11)\)和公式\((12)\)，得到新的运动方程和约束条件:

\[ \begin{align}& \left(E I \frac{\partial^4 X}{\partial x^4}\right)-\rho S \omega^2 X = 0\\& \left\{\begin{aligned} &X(0)=0 \\ &\frac{\partial^2 X(L)}{\partial x^2}=0 \\& \frac{\partial X(0)}{\partial x}=0 \\& E I \frac{\partial^3 X(L)}{\partial x^3}=K \cdot X(L) \end{aligned}\right. \end{align} \]

方程\((13)\)的解的通式为：

\[ X(x)=A \cos (k x)+B \sin (k x)+C \cosh (k x)+D \sinh (k x) \]

考虑初始条件：\(X(0)=0，\frac{\partial X(0)}{\partial x}=0\)，有：

\[ A+C=0 \quad C=-A，B+D=0 \quad D=-B \]

得到：

\[ X(x)=A[\cos (k x)-\cosh (k x)]+B[\sin (k x)-\sinh (k x)] \]

然后考虑初始条件：

\[ \left\{\begin{aligned}& \frac{\partial^2 X(L)}{\partial x^2}=0 \\& E I \frac{\partial^3 X(L)}{\partial x^3}=K \cdot X(L)\end{aligned}\right.\Rightarrow\left\{\begin{aligned} & A[-\cos (k L)-\cosh (k L)]+B[-\sin (k L)-\sinh (k L)]=0 \\ & A[\sin (k L)-\sinh (k L)]+B[-\cos (k L)-\cosh (k L)] \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \quad=\frac{K}{E I \cdot k^3}[A[\cos (k L)-\cosh (k L)]+B[\sin (k L)-\sinh (k L)]] \end{aligned}\right. \]

在这个模式下，可以得到：

\[ \left[1+\frac{1}{\cos (k L) \cdot \cosh (k L)}\right]+\frac{K}{E I \cdot k^3}[-\tan (k L)-\tanh (k L)]=0 \]

\[ \begin{aligned}& X_n(x) =A n\left[[\cos (k x)-\cosh (k x)]-[\sin (k x)-\sinh (k x)] * \frac{\cos \left(k_n L\right) \cosh \left(k_n L\right)}{\sin \left(k_n L\right)+\sinh \left(k_n L\right)}\right]\end{aligned} \]

模态分析

回到方程\((13)\)，使用\(k\)代替其他变量，并写成模态的形式：

\[ \frac{\partial^4 X_n}{\partial x^4}-k^2 X_n=0 \]

乘以\(X_p\)之后积分:

\[ \int_0^L\frac{\partial^4 X_n}{\partial x^4}X_pdx-k^2\int_0^L X_nX_pdx=0 \]

为了使第一项齐次，有：

\[ (A X_n, X_p)=\int_0^L \frac{\partial^4 X_n}{\partial x^4} X_p d x=\left[\frac{\partial^3 X_n}{\partial x^3} X_p\right]_0^L-\left[\frac{\partial^2 X_n}{\partial x^2} \frac{\partial X_p}{\partial x}\right]_0^L+\int_0^L \frac{\partial^2 X_n}{\partial x^2} \cdot \frac{\partial^2 X_p}{\partial x^2} d x \]

其中根据边界条件，有\(X_p = 0\)，\(\frac{\partial^2 X_n(L)}{\partial x^2} = 0\)，\(\frac{\partial X_p(0)}{\partial x} = 0\)，所以：

.

\[ \begin{align*}\left(A X_n, X_p\right)&=\frac{\partial^3 X_n(L)}{\partial x^3}X_p(L)+\int_0^L \frac{\partial^2 X_n}{\partial x^2} \cdot \frac{\partial^2 X_p}{\partial x^2} d x&\\&=\frac K {EI}X_n(L)X_p(L)+\int_0^L \frac{\partial^2 X_n}{\partial x^2} \cdot \frac{\partial^2 X_p}{\partial x^2} d x&\end{align*} \]

然后我们可以自由分配这些部分，比如假设：

\[ \begin{aligned}& a\left( X_n, X_p\right)=\int_0^L X_n^{\prime\prime} X_p^{\prime\prime} d n +\frac K{EI} X_n(L) X_p(L)\\& \left(X_n, X_p\right)=\int_0^L X_n X_p d r\end{aligned} \]

然后进一步的正交性的计算同上。

两端受到约束的曲梁的例子：使用模态基处理受力问题

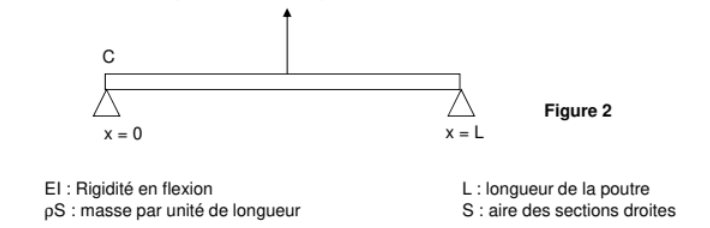
求通解

两端受到约束的曲量有：

$$ \[\begin{align}& \left(E I \frac{\partial^4 X}{\partial x^4}\right)-\rho S \omega^2 X = 0\\& \left\{\begin{aligned} &X(0)=0 \\&X(L) = 0 \\ &\frac{\partial^2 X(L)}{\partial x^2}=0 \\& \frac{\partial X^2(0)}{\partial x^2}=0 \end{aligned}\right. \end{align}\] $$

由\((16).1\)和\((16).3\)：

\[ A=C=0 \]

由\((16).2\)和\((16).4\)：

\[ \begin{gathered}B \cdot \sin (k L)+D \cdot \sinh (k L)=0 \\-k^2 \cdot B \cdot \sin (k L)+k^2 \cdot D \cdot \sinh (k L)=0\end{gathered} \]

得到：

\[ \left\{\begin{aligned}& B\sin (k L)=0 \\&D\sinh (k L)=0\end{aligned}\right.\Rightarrow\left\{\begin{aligned}& k_n=\frac{n \pi}{L}\\&D = 0\end{aligned}\right. \]

从而得到：

\[ X_n(x)=B_n \sin \left(k_n x\right) \quad k_n=\frac{n \pi}{L} \]

受力的情况

我们来考虑受力的情况：

\[ E I v^{(4)}+\rho S \ddot{v}=F \delta _{x=L / 2} \]

在模态基下，设：\(v(x, t)=\sum_n q_n X_n\)，得：

\[ E I \sum q_n x_n^{(4)}+\rho S \sum \ddot{q}_n x_n=F \delta_{x=L / 2} \]

对其进行变换\(\int_0^L x_i(\cdots) d x\)得：

\[ \omega_i^2 q_i+\ddot{q}_i =F X_i(L / 2) \]

假设：\(F=F_0 e^{i \omega t}\)，有\(q_i=Q_i e^{i \omega t}\)，原式得：

\[ \omega_i^2 Q_i-\omega^2 Q_i=F_0 x_i(L / 2) \]

解得：

\[ Q_i=\frac{F_0}{\omega_i^2-\omega^2} X_i(L / 2) \]

在这种情况下，位移：

\[ v(x, t)=\sum_i Q_i e^{i \omega t} \cdot x_i(x)=\sum_i \frac{F_0 e^{i \omega t}}{\omega_i^2-\omega^2} X_i(L /2)X_i(x) \]

当\(\omega \longrightarrow \omega_i\)，有：

\[ v(x, t) \longrightarrow \frac{F_0 e^{i \omega t}}{\omega_i^2-\omega^2} x_i(L / 2) x_i(x)\longrightarrow\infty \]

在模态\(i\)处有共振。

受力矩得情况

我们来考虑受力矩的情况：

\[ E I v^{(4)}+\rho s \ddot{v}=c \delta_{x=0}^{\prime} \]

代入模态基表示：

\[ EI \sum q_n X_n^{(4)}+\rho S \sum \ddot{q}_n X_n=c \delta_{x=0}^{\prime} \]

进行变换\(\int_0^L x_i(\ldots) d x\)得：

\[ \omega_i^2 q_i+\ddot{q}_i=c X_i^{\prime}(0) = \frac{i \pi}{L} B_i \cdot C \]

假设：\(C=C_0 e^{i \omega t}\)，有\(q=Q \cdot e^{i c u t}\)，从而解得：

\[ Q_i=\frac{C_0}{\omega_i^2-\omega^2} \frac{i \pi}{L} B_i \]

最终解为：

\[ V(x, t)=\sum_i \frac{C_0 e^{i \omega t}}{\omega_i^2-\omega^2} \frac{i \pi}{L} \cdot B_i^2 \sin \left(\frac{i \pi}{L} x\right) \]