CRS I 结构动力学问题的表述:强表述和弱表述 Formulation du problème en dynamique des structures : formulation forte / formulation faible
离散系统的差分方法 Approche différentielle sur les systèmes discrets
振动系统是离散组件的集合,唯一的特征是具有惯性的刚体,可变性元件(弹簧)和耗散元件连接在一起。未知数和自由度的数量与实体和连接方程的数量相关。
表述的描述 Description des formulations
强表述:离散系统
\[ M \ddot{u}=-k u+F \quad M \ddot{u}=-k u-c \dot{u} \]
弱表述:变分方法
从能量和功的概念出发,写出方程,根据变分原理写出平衡方程。
虚位移原理 Principe des travaux virtuels
变分算符 opérateur de variation与虚位移 déplacement virtuel
\[ \delta \mathrm{u}_{\mathrm{i}}=\tilde{\mathrm{u}}_{\mathrm{i}}(\mathrm{t})-\mathrm{u}_{\mathrm{i}}(\mathrm{t}) \]
\(\delta\) 被称为变分算符 opérateur de variation,\(\delta u_i\)被称为相对真实位移的变分 variation par rapport au déplacement réel。
需保证:\(\delta u_i\left(t_1\right)=0 \text { et } \delta u_i\left(t_2\right)=0\)
变分算符与微分是可交换的:
\[ \begin{aligned} \frac{\mathrm{d}}{\mathrm{dt}}\left(\delta \mathrm{u}_{\mathrm{i}}\right) & =\frac{\mathrm{d}}{\mathrm{dt}}\left(\tilde{\mathrm{u}}_{\mathrm{i}}\right)-\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{u}_{\mathrm{i}}\right)=\delta\left(\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{u}_{\mathrm{i}}\right)\right) \\ & =\dot{\tilde{\mathrm{u}}}_{\mathrm{i}}-\dot{\mathrm{u}}_{\mathrm{i}}=\delta \dot{\mathrm{u}}_{\mathrm{i}} \end{aligned} \]
虚力和虚功
一般来说,我们将力和功分别定义为:
\[ \begin{aligned}& F\left(u(x), u^{\prime}(x), \ldots, x\right) ,& J=\int_{x_1}^{x_2} F\left(u(x), u^{\prime}(x), \ldots, x\right) \cdot d x\end{aligned} \]
引入虚位移之后,虚力可以表示为:
\[ \delta F=\frac{\partial F}{\partial u} \delta u+\frac{\partial F}{\partial u^{\prime}} \delta u^{\prime}+\ldots \]
而虚功可以表示为:
\[ \delta J=\int_{x_1}^{x_2} \delta F . d x \]
虚位移原理 Principe des travaux virtuels
根据强表述:\(m \ddot{u}_i=X_i \quad \forall \mathrm{i} \in\{1,2,3\}\),有虚位移方程:
\[ \sum_{i=1}^3\left(m \ddot{u}_i-X_i\right) \cdot \delta u_i=0 \]
即在虚拟位移 \(u_i\) 实际作用在质点上的力所做的虚拟功为零。
\[ \left\{\left[\begin{array}{l}m \ddot{u}_1 \\m \ddot{u}_2 \\m \ddot{u}_3\end{array}\right]-\left[\begin{array}{l}\mathrm{X}_1 \\\mathrm{X}_2 \\\mathrm{X}_3\end{array}\right]\right\} \cdot\left\{\begin{array}{l}\delta \mathrm{u}_1 \\\delta \mathrm{u}_2 \\\delta \mathrm{u}_3\end{array}\right\}=\left\{\begin{array}{l}0 \\0 \\0\end{array}\right\} \]
如果虚拟功方程对于与运动学条件兼容的任何位移得到验证,则满足系统的平衡。
哈密顿原理
哈密顿原理是虚位移原理的对时间积分形式:
\[ \int_{\mathrm{t}_1}^{\mathrm{t}_2}\left[\sum_{\mathrm{k}=1}^{\mathrm{N}} \sum_{\mathrm{i}=1}^3\left(m \ddot{u}_i-X_i\right) \cdot \delta u_{ik}\right] \cdot \mathrm{dt}=0 \]
其中\(k\)表示物质上的\(k\)点,i表示方向。
\(u_{ik}\)是允许的虚位移 déplacement compatible ,即约束允许的位移
动能 Energie cinétique
可以观察到:
\[ \frac{d}{d t}\left(m_k \dot{u}_{i k} \cdot \delta u_{i k}\right)=m_k \ddot{u}_{i k} \delta u_{i k}+m_k \dot{u}_{i k} \delta \dot{u}_{i k}=m_k \ddot{u}_{i k} \delta u_{i k}+\delta\left(\frac{1}{2} m_k \dot{u}_{i k} \dot{u}_{i k}\right) \]
而后一项是动能的一部分,因此我们可以得到原式中的第一项:
\[ \int_{t_1}^{t_2}\left[\sum_{k=1}^N \sum_{i=1}^3\left(-m_k \ddot{u}_{i k}\right) \cdot \delta u_{i k}\right] \cdot d t=\left[-\sum_{k=1}^N \sum_{i=1}^3 m_k \dot{u}_{i k} \cdot \delta u_{i k}\right]_{t_1}^{t_2}+\delta \int_{t_1}^{t_2} E_c \cdot d t \]
功 Travail des actions mécaniques
对于原式的第二项,可以分成两项:外力做功\(\delta W_{\text {extérieur }}\)和有势力做功,即势能变化\(-\delta \mathrm{V}\)。
广义坐标
由于约束的存在,实际上的自由度并非原始的坐标数。因此引入自由度数量的广义坐标 coordonnée généralisée。
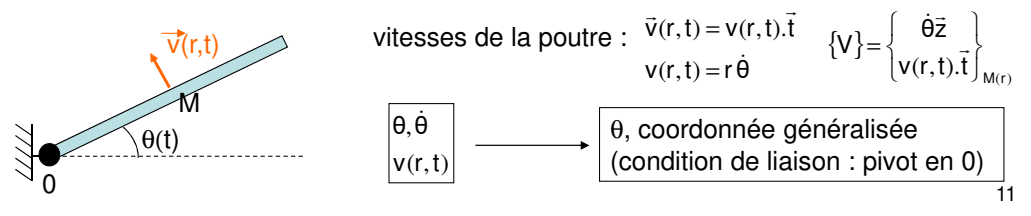
如上图,只有一个自由度的系统,可以选择与x轴夹角\(\theta(t)\)作为广义坐标。
通过广义坐标,原始的第二项可以写作:
\[ \sum_{\mathrm{k}=1}^{\mathrm{N}} \sum_{\mathrm{i}=1}^3 \mathrm{X}_{\mathrm{ik}} \cdot \delta \mathrm{u}_{\mathrm{ik}}=\sum_{\mathrm{S}=1}^{\mathrm{n}} \mathrm{Q}_{\mathrm{S}} \cdot \delta \mathrm{q}_{\mathrm{S}} \]
其中\(Q_s\)为广义力。同时,原始坐标的对时间微分可以写作:
\[ \mathrm{u}_{\mathrm{ik}}(\mathrm{x}, \mathrm{t})=\mathrm{U}_{\mathrm{ik}}\left(\mathrm{q}_{\mathrm{s}}, \mathrm{t}\right) \Rightarrow \dot{\mathrm{u}}_{\mathrm{ik}}=\frac{\partial \mathrm{U}_{\mathrm{ik}}}{\partial \mathrm{t}}+\sum_{\mathrm{S}=1}^{\mathrm{n}} \frac{\partial \mathrm{U}_{\mathrm{ik}}}{\partial \mathrm{q}_{\mathrm{s}}} \cdot \dot{\mathrm{q}}_{\mathrm{s}} \]
如果广义力是有势力,则可以写作:
\[ \sum_{S=1}^n Q_S \cdot \delta q_S=-\delta V\Leftrightarrow Q_S=-\frac{\partial V}{\partial q_S} \]
哈密顿原理 Enoncé du principe de Hamilton
根据以上描述,原始公式可以写作:
\[ \int_{t_1}^{t_2}\left[\sum_{k=1}^N \sum_{i=1}^3\left(-m_k \ddot{u}_{i k}+X_{i k}\right) \cdot \delta u_{i k}\right] \cdot d t=\left[-\sum_{k=1}^N \sum_{i=1}^3 m_k \dot{u}_{i k} \cdot \delta u_{i k}\right]_{t_1}^{t_2}+\delta \int_{t_1}^{t_2}\left(E_C-V+W_{e x t}\right) \cdot d t \]
然后根据条件:\(\begin{aligned}& \delta u_{i k}\left(t_1\right)=0 \\& \delta u_{i k}\left(t_2\right)=0\end{aligned}\),第一项为0。
由此我们得到了哈密顿原理的最终表述:
\[ \delta \int_{t_1}^{t_2}\left(E_C-V+W_{\text {ext }}\right) \cdot d t=0 \quad \text { avec } \quad \delta q_s\left(t_1\right)=0 \quad \text { et } \delta q_s\left(t_2\right)=0 \]
基于哈密顿原理的运动方程 Equations du mouvement à partir du principe de Hamilton
展开虚动能:
\[ \delta \mathrm{E}_{\mathrm{C}}=\sum_{\mathrm{S}=1}^{\mathrm{n}}\left(\frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \mathrm{q}_{\mathrm{s}}} \delta \mathrm{q}_{\mathrm{s}}+\frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \dot{\mathrm{q}}_{\mathrm{s}}} \delta \dot{\mathrm{q}}_{\mathrm{s}}\right) \]
展开外力做功:
\[ \delta W_{\text {ext }}=F_S \cdot \delta q_s \text { d'après } W_{\text {ext }}=F_S \cdot q_s \]
代入哈密顿原理得到:
\[ \int_{t_1}^{t_2}\left[\sum_{S=1}^n\left(\frac{\partial E_C}{\partial q_S}+Q_S+F_S\right) \delta q_S+\frac{\partial E_C}{\partial \dot{q}_S} \delta \dot{q}_S\right] d t=0 \]
基于分布积分法,第二项为:
\[ \frac{\partial E_C}{\partial \dot{q}_S} \delta \dot{q}_S = \left[\frac{\partial E_c}{\partial \dot{q}_s} \delta q_S\right]_{t_1}^{t_2}-\int_{t_1}^{t_2} \frac{d}{d t}\left(\frac{\partial E_C}{\partial \dot{q}_s}\right) \delta q_s \cdot d t \]
根据哈密顿原理,第一项为0,得到:
\[ \int_{t_1}^{t_2}\left[\sum_{S=1}^n\left(-\frac{d}{d t} \frac{\partial E_C}{\partial \dot{q}_S}+\frac{\partial E_C}{\partial q_S}+Q_S+F_S\right) \delta q_S\right] d t=0 \]
拉格朗日运动方程 Les équations du mouvement Lagrange
考虑每一个广义坐标:
\[ -\frac{\mathrm{d}}{\mathrm{dt}} \frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \dot{\mathrm{q}}_{\mathrm{S}}}+\frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \mathrm{q}_{\mathrm{S}}}+\mathrm{Q}_{\mathrm{S}}+\mathrm{F}_{\mathrm{S}}=0 \]
连续系统的情况
使用位移向量来表示物质的运动:
\[ \begin{aligned}& \vec{x}=\left\{\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right\} \\& \vec{u}=\left\{\begin{array}{l}u_1 \\u_2 \\u_3\end{array}\right\}=\left\{\begin{array}{l}u_1\left(x_1, x_2, x_3, t\right) \\u_2\left(x_1, x_2, x_3, t\right) \\u_3\left(x_1, x_2, x_3, t\right)\end{array}\right\}\end{aligned} \]
广义的哈莫顿原理
我们将哈莫顿原理中的:\(E_C-V+W_{\text {ext }}\)记为\(L(u)\)
动能
在连续系统中,动能可以分别被表示为:
\[ \begin{aligned}& \mathrm{E}_{\mathrm{C}}=\frac{1}{2} \int_{\Omega_0} \rho_0 \sum_{\mathrm{i}=1}^3 \dot{\mathrm{u}}_{\mathrm{i}} \dot{\mathrm{u}}_{\mathrm{i}} \mathrm{d} \Omega \end{aligned} \]
外势能
对于势能,有由体积力导致的外势能:
\[ V_{\text {ext }}=-\int_{\Omega_0} \sum_{\mathrm{i}=1}^3 \mathrm{f}_{\mathrm{i}} \cdot \mathrm{u}_{\mathrm{i}} \mathrm{d} \Omega \]
形变势能 énergie de déformation
有由内部形变导致的变形势能:
\[ \mathrm{V}_{\mathrm{int}}=\int_{\Omega_0} \mathrm{w}\left(\varepsilon_{\mathrm{ij}}\right) \mathrm{d} \Omega \]
其中\(\mathrm{w}\left(\varepsilon_{\mathrm{ij}}\right)\)是形变能密度,为:
\[ w\left(\varepsilon_{i j}\right)=\sum_{i, j} \int_0^{\varepsilon_{i j}} \sigma_{i j} d \varepsilon_{i j} \Rightarrow \delta w=\sum_{i, j} \frac{\partial w}{\partial \varepsilon_{i j}} \delta \varepsilon_{i j} \]
外力做功
外力做功可以表示为:
\[ \mathrm{W}_{\mathrm{ext}}=\int_{\partial \Omega_0} \sum^3 \mathrm{~F}_{\mathrm{i}} \cdot \mathrm{u}_{\mathrm{i}} \mathrm{d} \partial \Omega \]
广义的哈莫顿原理
最终代入这些元素后,得到广义的哈莫顿原理,即为弱表述:
\[ \begin{aligned}\delta \int_{t_1}^{t_2} & \left(E_C-V+W_{e x t}\right) \cdot d t \\& =\int_{t_1}^{t_2} \int_{\partial \Omega_0} \sum_{i, j}\left(F_j-n_i \sigma_{i j}\right) \delta u_j d \partial \Omega d t+\int_{t_1}^{t_2} \int_{\Omega_0} \sum_{j=1}^3\left(\sum_{i=1}^3 \frac{\partial \sigma_{i j}}{\partial x_i}-\rho_0 \ddot{u}_j+f_j\right) \delta u_j d \Omega d t\end{aligned} \]
- 第一个积分项是对物体表面 \(∂Ω_0\) 上的力的贡献进行积分。它表示了表面力对位移的影响,即力对位移的功。
- 第二个积分项是对物体内部 \(∂Ω_0\)区域内的力的贡献进行积分。它表示了内部应力和体积力对位移的影响,即内部力对位移的功。
拉伸,弯曲的动力学方程和边界条件求法
拉伸压缩杆的例子

我们应用广义的哈莫顿原理解决这个问题:
\[ \delta \int_{t_1}^{t_2}\left(E_C-V+W_{e x t}\right) \cdot d t = 0 \]
首先,我们要计算动能,势能和外力做功。
动能
在这个连续系统中,动能被定义为:
\[ E_C=\frac{1}{2} \int_{\Omega}\rho\left(\frac{\partial u(x,t)}{\partial t}\right)^2d\Omega = \frac{1}{2} \int_{0}^L\rho S\left(\frac{\partial u(x,t)}{\partial t}\right)^2dx \]
形式上与质点的动能一致。
势能
在这个系统中,势能由\(x\)方向的形变提供:
\[ V = V_{int} = \frac 12 \int_{\Omega}\sigma : \varepsilon d\Omega \]
其中有:
\[ \varepsilon = \frac{\partial u(x, t)}{\partial tx}, \ \sigma = E\varepsilon \]
得到:
\[ V = V_{int} = \frac 12 \int_{0}^LES\left(\frac{\partial u(x, t)}{\partial x}\right)^2dx \]
外力做功
\(x = 0\)点的约束力不做功,\(x = L\)的力:
\[ F_L = M\frac{d^2 u(L, t)}{d t^2} \]
其做功:
\[ W_{ext} = F_Lu(L,t) = M \frac{d^2 u(L, t)}{d t^2}u(L,t) \]
哈莫顿原理
根据哈莫顿原理,有:
\[ \begin{align} & \delta \int_{t_1}^{t_2}\left(E_C-V+W_{e x t}\right) \cdot d t=0 \nonumber \\& \int_{t_1}^{t_2}\int_{0}^{L}\rho S\dot u\delta\dot udtdx-\int_{t_1}^{t_2}\int_{0}^{L}ES\frac{\partial u(x, t)}{\partial x}\delta\left(\frac{\partial u(x, t)}{\partial x}\right)dxdt \\& \ \ \ \ \ \ \ \ \ +\int_{t_1}^{t_2}F_L\delta u(L,t)dt = 0 \nonumber \end{align} \]
对\((1)\)第一项应用分步积分,目的是消除变分符号中的对时间的偏微分:
\[ \begin{align}\int_{t_1}^{t_2} \int_0^L \rho S \dot{u} \delta \dot{u} d t d x = \left[\int_0^L\rho S \dot{u} \delta ud x\right]_{t_1}^{t_2}-\int_{t_1}^{t_2} \int_0^L \rho S \ddot{u} \delta u d t d x\end{align} \]
根据\(\delta u(x,t_1) = 0,\delta u(x,t_2) = 0\),\((2)\)的第一项为\(0\)。
对\((1)\)的第二项应用分步积分,目的是消除变分符号中对空间的偏微分:
\[ \begin{align} -\int_{t_1}^{t_2} &\int_0^L E S \frac{\partial u(x, t)}{\partial x} \delta\left(\frac{\partial u(x, t)}{\partial x}\right) d x d t = \nonumber\\&- \left[\int_{t_1}^{t_2}E S \frac{\partial u(x, t)}{\partial x} \delta u d t\right]_0^L + \int_{t_1}^{t_2} \int_0^L E S \frac{\partial^2 u(x, t)}{\partial x^2} \delta u d x d t \end{align} \]
进一步展开\((3)\)的第一项:
\[ -\left[\int_{t_1}^{t_2} E S \frac{\partial u(x, t)}{\partial x} \delta u d t\right]_0^L = \int_{t_1}^{t_2} E S \frac{\partial u(0, t)}{\partial x} \delta u(0,t) d t-\int_{t_1}^{t_2} E S \frac{\partial u(L, t)}{\partial x} \delta u(L,t) d t \]
最终得到:
\[ \begin{align}&-\int_{t_1}^{t_2} \int_0^L \rho S \ddot{u} \delta u d t d x + \int_{t_1}^{t_2} \int_0^L E S \frac{\partial^2 u(x, t)}{\partial x^2} \delta u d x d t+ \nonumber \\& \int_{t_1}^{t_2} E S \frac{\partial u(0, t)}{\partial x} \delta u(0,t) d t - \int_{t_1}^{t_2} E S \frac{\partial u(L, t)}{\partial x} \delta u(L,t) d t +\nonumber\\& \int_{t_1}^{t_2} F_L \delta u(L, t) d t = 0 \end{align} \]
合并同类项:
\[ \begin{align}&-\int_{t_1}^{t_2} \int_0^L \left(\rho S \ddot{u} - E S \frac{\partial^2 u(x, t)}{\partial x^2}\right) \delta u d x d t+ \nonumber \int_{t_1}^{t_2} E S \frac{\partial u(0, t)}{\partial x} \delta u(0,t) d t -\\& \int_{t_1}^{t_2} \left(E S \frac{\partial u(L, t)}{\partial x} - F_L \right)\delta u(L, t) d t = 0 \end{align} \]
从而得到运动方程\((6)\)和边界条件\((7)\):
\[ \begin{align} &\rho S \ddot{u}-E S \frac{\partial^2 u(x, t)}{\partial x^2} = 0 \\ & \left\{ \begin{aligned} &ES\frac{\partial u(0,t)}{\partial x}\delta u(0,t) = 0 \Rightarrow u(0,t) = 0 \\ & E S \frac{\partial u(L, t)}{\partial x}-F_L = 0 \Rightarrow E S \frac{\partial u(L, t)}{\partial x}=F_L \end{aligned} \right. \end{align} \]
曲梁的例子
动能,势能和所受外力做功
动能与压缩拉伸杆的处理方式相同:
\[ E_c=\frac{1}{2} \int_0^L \rho s \dot{v}^2 d x \]
处理势能时需要注意,势能沿x方向累计,所以我们要求出x方向位移和\(v\)的关系。
\[ u=-\omega y=-\frac{\partial v}{\partial x} y \]
然后以相同的方法求出应力和应变:
\[ \varepsilon=\frac{\partial u}{\partial x}=-\frac{\partial^2 v}{\partial x^2} y, \ \ \sigma=E \varepsilon=-E\frac{\partial^2 v}{ \partial x^2} y \]
从而得到势能:
\[ V=\frac{1}{2} \int_{\Omega} \sigma: \varepsilon d \Omega=\frac{1}{2} \int_0^L \int_s y^2E\left(\frac{\partial^2 v}{\partial x^2}\right)^2 d S d x \]
由于位移沿垂直x方向并非均匀,我们设\(\int_s y^2 d s=I\),从而得到势能的最终表述:
\[ V=\frac{1}{2} \int_0^L E I\left(\frac{\partial^2 v}{\partial x^2}\right)^2 d x \]
外力做功可以直接使用弹性势能的变化量来表示:
\[ W_{ext} = -V_{spring} = -\frac 12kv(L,t)^2 \]
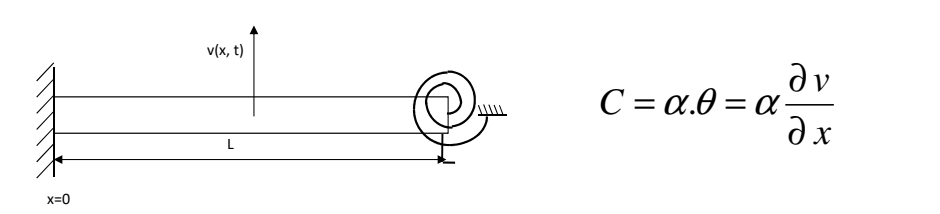
我们也同时处理一下这个情况:
\[ W_{ext} = -\frac{1}{2}\alpha \left(\frac{\partial v(L,t)}{\partial x}\right)^2 \]
最后我们与假设力为常数的情况比较:
\[ W_{ext} = F_0v(L,t) \]
哈密顿原理
应用哈莫顿原理,得到:
\[ \int_{t_1}^{t_2} \int_0^L \rho \delta \dot{v} \delta \dot{v} d x-\int_0^L E I \frac{\partial^2 v}{\partial x^2} \delta\left(\frac{\partial^2 v}{\partial x^2}\right) d x+F_0 \delta v(L, t) d t=0 \]
首项的处理方式与前一道题一致:
\[ \int_{t_1}^{t_2} \int_0^L \rho \delta \dot{v} \delta \dot{v} d x = \left[\int_0^L \rho \dot{v} \delta v d x\right]_{t_1}^{t_2}-\int_{t_1}^{t_2} \int_0^L \rho \ddot{v} \delta v d x \]
其中第一项为0。
第二项为了消除变分中的二阶导,我们要进行两次分部积分:
\[ -\int_{t_1}^{t_2}\int_0^L E I \frac{\partial^2 v}{\partial x^2} \delta\left(\frac{\partial^2 v}{\partial x^2}\right) d x = -\left[\int_{t_1}^{t_2} E I \frac{\partial^2 v}{\partial x^2} \delta\left(\frac{\partial v}{\partial x}\right) d t\right]^L_0+\left[\int_{t_1}^{t_2} E I \frac{\partial^3 v}{\partial x^3} \delta v d t\right]^L_0-\int_{t_1}^{t_2} \int_0^L E I \frac{\partial^4 v}{\partial x^4} \delta v d x d t \]
第三项对应另外两种情况将分别为:
\[ \int_{t_1}^{t_2}kv(L,t)\delta v(L,t) \]
和
\[ \int_{t_1}^{t_2}\alpha\frac{\partial v(L,t)}{\partial x}\delta\left(\frac{\partial v(L,t)}{\partial x}\right)dt \]
最终合并同类项之后,得到与受力无关的运动方程:
\[ E I \frac{\partial^h v}{\partial x^4}+\rho s \ddot{v}=0 \]
和约束条件:
\[ \begin{align} &-E I \frac{\partial^3 v(0,t)}{\partial x^3} \delta v(0,t) = 0 \Rightarrow v(0,t) = 0 \\& +E I \frac{\partial^2 v(0,t)}{\partial x^2} \delta\left(\frac{\partial v(0,t)}{\partial x}\right)=0\Rightarrow \frac{\partial v(0,t)}{\partial x} = 0 \end{align} \]
这两个约束条件和受力无关,以及于受力相关的:
\[ \begin{align} &\left(E I \frac{\partial^3 v(L,t)}{\partial x^3}+F_0||-kv(L,t)||0\right) \delta v=0\nonumber \\& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow E I \frac{\partial^3 v}{\partial x^3}(L, t)=-F_0||kv(L,t)||0 \end{align} \]
\(A||B||C\)分别代表受恒定外力、受弹簧提供的外力和受力矩作用的情况。最后是关于力矩的:
\[ \begin{align}(-E I &\frac{\partial^2 v(L,t)}{\partial x^2}-\alpha \frac{\partial v(L,t)}{\partial x}) \delta\left(\frac{\partial v(L,t)}{\partial x}\right) = 0\nonumber \\& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow -E I \frac{\partial^2 v(L,t)}{\partial x^2}=\alpha \frac{\partial v(L,t)}{\partial x} \end{align} \]
如果不受力矩,则直接有:
\[ \frac{\partial^2 v(L,t)}{\partial x^2} = 0 \]
对应两个受力的情况。



