离散系统的差分方法 Approche différentielle sur les systèmes discrets

[{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fcrs-1%2FUntitled.png","alt":""},{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fcrs-1%2FUntitled_1.png","alt":""},{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fcrs-1%2FUntitled_2.png","alt":""}]

振动系统是离散组件的集合，唯一的特征是具有惯性的刚体，可变性元件（弹簧）和耗散元件连接在一起。未知数和自由度的数量与实体和连接方程的数量相关。

表述的描述 Description des formulations

强表述：离散系统

$M \ddot{u}=-k u+F \quad M \ddot{u}=-k u-c \dot{u}$

弱表述：变分方法

从能量和功的概念出发，写出方程，根据变分原理写出平衡方程。

虚位移原理 Principe des travaux virtuels

变分算符 opérateur de variation与虚位移 déplacement virtuel

$\delta \mathrm{u}_{\mathrm{i}}=\tilde{\mathrm{u}}_{\mathrm{i}}(\mathrm{t})-\mathrm{u}_{\mathrm{i}}(\mathrm{t})$

$\delta$ 被称为变分算符 opérateur de variation，$\delta u_i$被称为相对真实位移的变分 variation par rapport au déplacement réel。

需保证：$\delta u_i\left(t_1\right)=0 \text { et } \delta u_i\left(t_2\right)=0$

变分算符与微分是可交换的：

$\begin{aligned} \frac{\mathrm{d}}{\mathrm{dt}}\left(\delta \mathrm{u}_{\mathrm{i}}\right) & =\frac{\mathrm{d}}{\mathrm{dt}}\left(\tilde{\mathrm{u}}_{\mathrm{i}}\right)-\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{u}_{\mathrm{i}}\right)=\delta\left(\frac{\mathrm{d}}{\mathrm{dt}}\left(\mathrm{u}_{\mathrm{i}}\right)\right) \\ & =\dot{\tilde{\mathrm{u}}}_{\mathrm{i}}-\dot{\mathrm{u}}_{\mathrm{i}}=\delta \dot{\mathrm{u}}_{\mathrm{i}} \end{aligned}$

虚力和虚功

一般来说，我们将力和功分别定义为：

$\begin{aligned}& F\left(u(x), u^{\prime}(x), \ldots, x\right) ，& J=\int_{x_1}^{x_2} F\left(u(x), u^{\prime}(x), \ldots, x\right) \cdot d x\end{aligned}$

引入虚位移之后，虚力可以表示为：

$\delta F=\frac{\partial F}{\partial u} \delta u+\frac{\partial F}{\partial u^{\prime}} \delta u^{\prime}+\ldots$

而虚功可以表示为：

$\delta J=\int_{x_1}^{x_2} \delta F . d x$

虚位移原理 Principe des travaux virtuels

根据强表述：$m \ddot{u}_i=X_i \quad \forall \mathrm{i} \in{1,2,3}$，有虚位移方程：

$\sum_{i=1}^3\left(m \ddot{u}_i-X_i\right) \cdot \delta u_i=0$

即在虚拟位移 $u_i$ 实际作用在质点上的力所做的虚拟功为零。

$\left\{\left[\begin{array}{l}m \ddot{u}_1 \\m \ddot{u}_2 \\m \ddot{u}_3\end{array}\right]-\left[\begin{array}{l}\mathrm{X}_1 \\\mathrm{X}_2 \\\mathrm{X}_3\end{array}\right]\right\} \cdot\left\{\begin{array}{l}\delta \mathrm{u}_1 \\\delta \mathrm{u}_2 \\\delta \mathrm{u}_3\end{array}\right\}=\left\{\begin{array}{l}0 \\0 \\0\end{array}\right\}$

如果虚拟功方程对于与运动学条件兼容的任何位移得到验证，则满足系统的平衡。

哈密顿原理

哈密顿原理是虚位移原理的对时间积分形式：

$\int_{\mathrm{t}_1}^{\mathrm{t}_2}\left[\sum_{\mathrm{k}=1}^{\mathrm{N}} \sum_{\mathrm{i}=1}^3\left(m \ddot{u}_i-X_i\right) \cdot \delta u_{ik}\right] \cdot \mathrm{dt}=0$

其中$k$表示物质上的$k$点，i表示方向。

$u_{ik}$是允许的虚位移 déplacement compatible ，即约束允许的位移

动能 Energie cinétique

可以观察到：

$\frac{d}{d t}\left(m_k \dot{u}_{i k} \cdot \delta u_{i k}\right)=m_k \ddot{u}_{i k} \delta u_{i k}+m_k \dot{u}_{i k} \delta \dot{u}_{i k}=m_k \ddot{u}_{i k} \delta u_{i k}+\delta\left(\frac{1}{2} m_k \dot{u}_{i k} \dot{u}_{i k}\right)$

而后一项是动能的一部分，因此我们可以得到原式中的第一项：

$\int_{t_1}^{t_2}\left[\sum_{k=1}^N \sum_{i=1}^3\left(-m_k \ddot{u}_{i k}\right) \cdot \delta u_{i k}\right] \cdot d t=\left[-\sum_{k=1}^N \sum_{i=1}^3 m_k \dot{u}_{i k} \cdot \delta u_{i k}\right]_{t_1}^{t_2}+\delta \int_{t_1}^{t_2} E_c \cdot d t$

功 Travail des actions mécaniques

对于原式的第二项，可以分成两项：外力做功$\delta W_{\text {extérieur }}$和有势力做功，即势能变化$-\delta \mathrm{V}$。

广义坐标

由于约束的存在，实际上的自由度并非原始的坐标数。因此引入自由度数量的广义坐标 coordonnée généralisée。

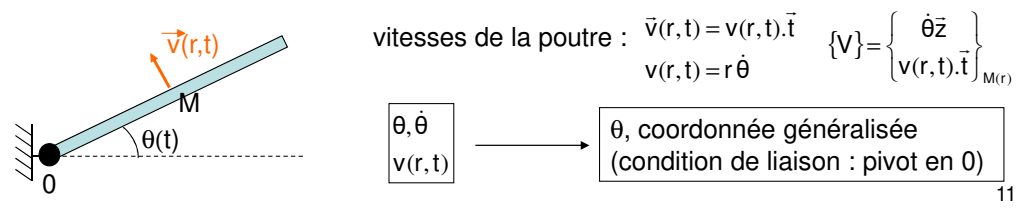
如上图，只有一个自由度的系统，可以选择与x轴夹角$\theta(t)$作为广义坐标。

通过广义坐标，原始的第二项可以写作：

$\sum_{\mathrm{k}=1}^{\mathrm{N}} \sum_{\mathrm{i}=1}^3 \mathrm{X}_{\mathrm{ik}} \cdot \delta \mathrm{u}_{\mathrm{ik}}=\sum_{\mathrm{S}=1}^{\mathrm{n}} \mathrm{Q}_{\mathrm{S}} \cdot \delta \mathrm{q}_{\mathrm{S}}$

其中$Q_s$为广义力。同时，原始坐标的对时间微分可以写作：

$\mathrm{u}_{\mathrm{ik}}(\mathrm{x}, \mathrm{t})=\mathrm{U}_{\mathrm{ik}}\left(\mathrm{q}_{\mathrm{s}}, \mathrm{t}\right) \Rightarrow \dot{\mathrm{u}}_{\mathrm{ik}}=\frac{\partial \mathrm{U}_{\mathrm{ik}}}{\partial \mathrm{t}}+\sum_{\mathrm{S}=1}^{\mathrm{n}} \frac{\partial \mathrm{U}_{\mathrm{ik}}}{\partial \mathrm{q}_{\mathrm{s}}} \cdot \dot{\mathrm{q}}_{\mathrm{s}}$

如果广义力是有势力，则可以写作：

$\sum_{S=1}^n Q_S \cdot \delta q_S=-\delta V\Leftrightarrow Q_S=-\frac{\partial V}{\partial q_S}$

哈密顿原理 Enoncé du principe de Hamilton

根据以上描述，原始公式可以写作：

$\int_{t_1}^{t_2}\left[\sum_{k=1}^N \sum_{i=1}^3\left(-m_k \ddot{u}_{i k}+X_{i k}\right) \cdot \delta u_{i k}\right] \cdot d t=\left[-\sum_{k=1}^N \sum_{i=1}^3 m_k \dot{u}_{i k} \cdot \delta u_{i k}\right]_{t_1}^{t_2}+\delta \int_{t_1}^{t_2}\left(E_C-V+W_{e x t}\right) \cdot d t$

然后根据条件：$\begin{aligned}& \delta u{i k}\left(t_1\right)=0 \& \delta u{i k}\left(t_2\right)=0\end{aligned}$，第一项为0。

由此我们得到了哈密顿原理的最终表述：

$\delta \int_{t_1}^{t_2}\left(E_C-V+W_{\text {ext }}\right) \cdot d t=0 \quad \text { avec } \quad \delta q_s\left(t_1\right)=0 \quad \text { et } \delta q_s\left(t_2\right)=0$

基于哈密顿原理的运动方程 Equations du mouvement à partir du principe de Hamilton

展开虚动能：

$\delta \mathrm{E}_{\mathrm{C}}=\sum_{\mathrm{S}=1}^{\mathrm{n}}\left(\frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \mathrm{q}_{\mathrm{s}}} \delta \mathrm{q}_{\mathrm{s}}+\frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \dot{\mathrm{q}}_{\mathrm{s}}} \delta \dot{\mathrm{q}}_{\mathrm{s}}\right)$

展开外力做功：

$\delta W_{\text {ext }}=F_S \cdot \delta q_s \text { d'après } W_{\text {ext }}=F_S \cdot q_s$

代入哈密顿原理得到：

$\int_{t_1}^{t_2}\left[\sum_{S=1}^n\left(\frac{\partial E_C}{\partial q_S}+Q_S+F_S\right) \delta q_S+\frac{\partial E_C}{\partial \dot{q}_S} \delta \dot{q}_S\right] d t=0$

基于分布积分法，第二项为：

$\frac{\partial E_C}{\partial \dot{q}_S} \delta \dot{q}_S = \left[\frac{\partial E_c}{\partial \dot{q}_s} \delta q_S\right]_{t_1}^{t_2}-\int_{t_1}^{t_2} \frac{d}{d t}\left(\frac{\partial E_C}{\partial \dot{q}_s}\right) \delta q_s \cdot d t$

根据哈密顿原理，第一项为0，得到：

$\int_{t_1}^{t_2}\left[\sum_{S=1}^n\left(-\frac{d}{d t} \frac{\partial E_C}{\partial \dot{q}_S}+\frac{\partial E_C}{\partial q_S}+Q_S+F_S\right) \delta q_S\right] d t=0$

拉格朗日运动方程 Les équations du mouvement Lagrange

考虑每一个广义坐标：

$-\frac{\mathrm{d}}{\mathrm{dt}} \frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \dot{\mathrm{q}}_{\mathrm{S}}}+\frac{\partial \mathrm{E}_{\mathrm{C}}}{\partial \mathrm{q}_{\mathrm{S}}}+\mathrm{Q}_{\mathrm{S}}+\mathrm{F}_{\mathrm{S}}=0$

连续系统的情况

使用位移向量来表示物质的运动：

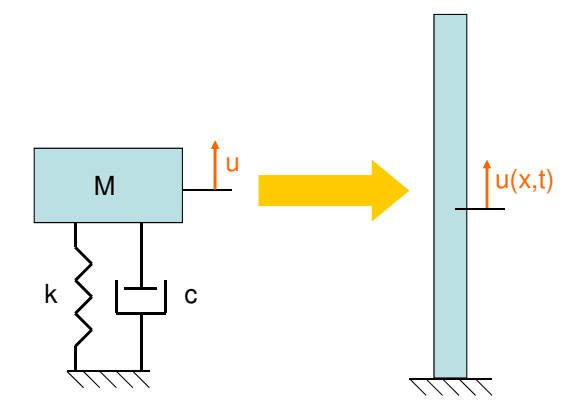
$\begin{aligned}& \vec{x}=\left\{\begin{array}{l}x_1 \\x_2 \\x_3\end{array}\right\} \\& \vec{u}=\left\{\begin{array}{l}u_1 \\u_2 \\u_3\end{array}\right\}=\left\{\begin{array}{l}u_1\left(x_1, x_2, x_3, t\right) \\u_2\left(x_1, x_2, x_3, t\right) \\u_3\left(x_1, x_2, x_3, t\right)\end{array}\right\}\end{aligned}$

广义的哈莫顿原理

我们将哈莫顿原理中的：$EC-V+W{\text {ext }}$记为$L(u)$

动能

在连续系统中，动能可以分别被表示为：

$\begin{aligned}& \mathrm{E}_{\mathrm{C}}=\frac{1}{2} \int_{\Omega_0} \rho_0 \sum_{\mathrm{i}=1}^3 \dot{\mathrm{u}}_{\mathrm{i}} \dot{\mathrm{u}}_{\mathrm{i}} \mathrm{d} \Omega \end{aligned}$

外势能

对于势能，有由体积力导致的外势能：

$V_{\text {ext }}=-\int_{\Omega_0} \sum_{\mathrm{i}=1}^3 \mathrm{f}_{\mathrm{i}} \cdot \mathrm{u}_{\mathrm{i}} \mathrm{d} \Omega$

形变势能 énergie de déformation

有由内部形变导致的变形势能：

$\mathrm{V}_{\mathrm{int}}=\int_{\Omega_0} \mathrm{w}\left(\varepsilon_{\mathrm{ij}}\right) \mathrm{d} \Omega$

其中$\mathrm{w}\left(\varepsilon_{\mathrm{ij}}\right)$是形变能密度，为：

$w\left(\varepsilon_{i j}\right)=\sum_{i, j} \int_0^{\varepsilon_{i j}} \sigma_{i j} d \varepsilon_{i j} \Rightarrow \delta w=\sum_{i, j} \frac{\partial w}{\partial \varepsilon_{i j}} \delta \varepsilon_{i j}$

外力做功

外力做功可以表示为：

$\mathrm{W}_{\mathrm{ext}}=\int_{\partial \Omega_0} \sum^3 \mathrm{~F}_{\mathrm{i}} \cdot \mathrm{u}_{\mathrm{i}} \mathrm{d} \partial \Omega$

广义的哈莫顿原理

最终代入这些元素后，得到广义的哈莫顿原理，即为弱表述：

$\begin{aligned}\delta \int_{t_1}^{t_2} & \left(E_C-V+W_{e x t}\right) \cdot d t \\& =\int_{t_1}^{t_2} \int_{\partial \Omega_0} \sum_{i, j}\left(F_j-n_i \sigma_{i j}\right) \delta u_j d \partial \Omega d t+\int_{t_1}^{t_2} \int_{\Omega_0} \sum_{j=1}^3\left(\sum_{i=1}^3 \frac{\partial \sigma_{i j}}{\partial x_i}-\rho_0 \ddot{u}_j+f_j\right) \delta u_j d \Omega d t\end{aligned}$

第一个积分项是对物体表面 $∂Ω_0$ 上的力的贡献进行积分。它表示了表面力对位移的影响，即力对位移的功。
第二个积分项是对物体内部 $∂Ω_0$区域内的力的贡献进行积分。它表示了内部应力和体积力对位移的影响，即内部力对位移的功。

拉伸，弯曲的动力学方程和边界条件求法

拉伸压缩杆的例子

我们应用广义的哈莫顿原理解决这个问题：

$\delta \int_{t_1}^{t_2}\left(E_C-V+W_{e x t}\right) \cdot d t = 0$

首先，我们要计算动能，势能和外力做功。

动能

在这个连续系统中，动能被定义为：

$E_C=\frac{1}{2} \int_{\Omega}\rho\left(\frac{\partial u(x,t)}{\partial t}\right)^2d\Omega = \frac{1}{2} \int_{0}^L\rho S\left(\frac{\partial u(x,t)}{\partial t}\right)^2dx$

形式上与质点的动能一致。

势能

在这个系统中，势能由$x$方向的形变提供：

$V = V_{int} = \frac 12 \int_{\Omega}\sigma : \varepsilon d\Omega$

其中有：

$\varepsilon = \frac{\partial u(x, t)}{\partial tx}, \ \sigma = E\varepsilon$

得到：

$V = V_{int} = \frac 12 \int_{0}^LES\left(\frac{\partial u(x, t)}{\partial x}\right)^2dx$

外力做功

$x = 0$点的约束力不做功，$x = L$的力：

$F_L = M\frac{d^2 u(L, t)}{d t^2}$

其做功：

$W_{ext} = F_Lu(L,t) = M \frac{d^2 u(L, t)}{d t^2}u(L,t)$

哈莫顿原理

根据哈莫顿原理，有：

$\begin{align} & \delta \int_{t_1}^{t_2}\left(E_C-V+W_{e x t}\right) \cdot d t=0 \nonumber \\& \int_{t_1}^{t_2}\int_{0}^{L}\rho S\dot u\delta\dot udtdx-\int_{t_1}^{t_2}\int_{0}^{L}ES\frac{\partial u(x, t)}{\partial x}\delta\left(\frac{\partial u(x, t)}{\partial x}\right)dxdt \\& \ \ \ \ \ \ \ \ \ +\int_{t_1}^{t_2}F_L\delta u(L,t)dt = 0 \nonumber \end{align}$

对$(1)$第一项应用分步积分，目的是消除变分符号中的对时间的偏微分：

$\begin{align}\int_{t_1}^{t_2} \int_0^L \rho S \dot{u} \delta \dot{u} d t d x = \left[\int_0^L\rho S \dot{u} \delta ud x\right]_{t_1}^{t_2}-\int_{t_1}^{t_2} \int_0^L \rho S \ddot{u} \delta u d t d x\end{align}$

根据$\delta u(x,t_1) = 0,\delta u(x,t_2) = 0$，$(2)$的第一项为$0$。

对$(1)$的第二项应用分步积分，目的是消除变分符号中对空间的偏微分：

$\begin{align} -\int_{t_1}^{t_2} &\int_0^L E S \frac{\partial u(x, t)}{\partial x} \delta\left(\frac{\partial u(x, t)}{\partial x}\right) d x d t = \nonumber\\&- \left[\int_{t_1}^{t_2}E S \frac{\partial u(x, t)}{\partial x} \delta u d t\right]_0^L + \int_{t_1}^{t_2} \int_0^L E S \frac{\partial^2 u(x, t)}{\partial x^2} \delta u d x d t \end{align}$

进一步展开$(3)$的第一项：

$-\left[\int_{t_1}^{t_2} E S \frac{\partial u(x, t)}{\partial x} \delta u d t\right]_0^L = \int_{t_1}^{t_2} E S \frac{\partial u(0, t)}{\partial x} \delta u(0,t) d t-\int_{t_1}^{t_2} E S \frac{\partial u(L, t)}{\partial x} \delta u(L,t) d t$

最终得到：

$\begin{align}&-\int_{t_1}^{t_2} \int_0^L \rho S \ddot{u} \delta u d t d x + \int_{t_1}^{t_2} \int_0^L E S \frac{\partial^2 u(x, t)}{\partial x^2} \delta u d x d t+ \nonumber \\& \int_{t_1}^{t_2} E S \frac{\partial u(0, t)}{\partial x} \delta u(0,t) d t - \int_{t_1}^{t_2} E S \frac{\partial u(L, t)}{\partial x} \delta u(L,t) d t +\nonumber\\& \int_{t_1}^{t_2} F_L \delta u(L, t) d t = 0 \end{align}$

合并同类项：

$\begin{align}&-\int_{t_1}^{t_2} \int_0^L \left(\rho S \ddot{u} - E S \frac{\partial^2 u(x, t)}{\partial x^2}\right) \delta u d x d t+ \nonumber \int_{t_1}^{t_2} E S \frac{\partial u(0, t)}{\partial x} \delta u(0,t) d t -\\& \int_{t_1}^{t_2} \left(E S \frac{\partial u(L, t)}{\partial x} - F_L \right)\delta u(L, t) d t = 0 \end{align}$

从而得到运动方程$(6)$和边界条件$(7)$：

$\begin{align} &\rho S \ddot{u}-E S \frac{\partial^2 u(x, t)}{\partial x^2} = 0 \\ & \left\{ \begin{aligned} &ES\frac{\partial u(0,t)}{\partial x}\delta u(0,t) = 0 \Rightarrow u(0,t) = 0 \\ & E S \frac{\partial u(L, t)}{\partial x}-F_L = 0 \Rightarrow E S \frac{\partial u(L, t)}{\partial x}=F_L \end{aligned} \right. \end{align}$

曲梁的例子

[{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fcrs-1%2FUntitled_6.png","alt":""},{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fcrs-1%2FUntitled_7.png","alt":""},{"url":"https://raphaelhyaan-1322456377.cos.ap-beijing.myqcloud.com/post%2Fcrs-1%2FUntitled_8.png","alt":""}]

动能，势能和所受外力做功

动能与压缩拉伸杆的处理方式相同：
$E_c=\frac{1}{2} \int_0^L \rho s \dot{v}^2 d x$
处理势能时需要注意，势能沿x方向累计，所以我们要求出x方向位移和$v$的关系。
$u=-\omega y=-\frac{\partial v}{\partial x} y$
然后以相同的方法求出应力和应变：
$\varepsilon=\frac{\partial u}{\partial x}=-\frac{\partial^2 v}{\partial x^2} y, \ \ \sigma=E \varepsilon=-E\frac{\partial^2 v}{ \partial x^2} y$
从而得到势能：
$V=\frac{1}{2} \int_{\Omega} \sigma: \varepsilon d \Omega=\frac{1}{2} \int_0^L \int_s y^2E\left(\frac{\partial^2 v}{\partial x^2}\right)^2 d S d x$
由于位移沿垂直x方向并非均匀，我们设$\int_s y^2 d s=I$，从而得到势能的最终表述：
$V=\frac{1}{2} \int_0^L E I\left(\frac{\partial^2 v}{\partial x^2}\right)^2 d x$
外力做功可以直接使用弹性势能的变化量来表示：
$W_{ext} = -V_{spring} = -\frac 12kv(L,t)^2$

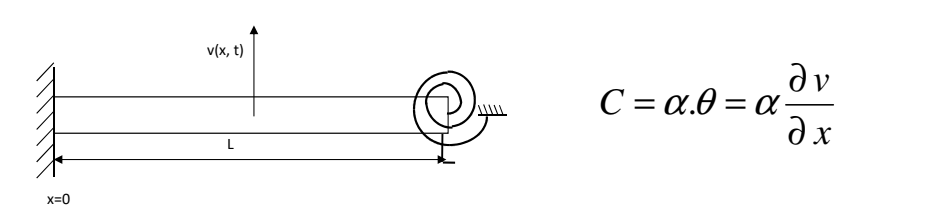
我们也同时处理一下这个情况：
$W_{ext} = -\frac{1}{2}\alpha \left(\frac{\partial v(L,t)}{\partial x}\right)^2$
最后我们与假设力为常数的情况比较：
$W_{ext} = F_0v(L,t)$

哈密顿原理

应用哈莫顿原理，得到：

$\int_{t_1}^{t_2} \int_0^L \rho \delta \dot{v} \delta \dot{v} d x-\int_0^L E I \frac{\partial^2 v}{\partial x^2} \delta\left(\frac{\partial^2 v}{\partial x^2}\right) d x+F_0 \delta v(L, t) d t=0$

首项的处理方式与前一道题一致：

$\int_{t_1}^{t_2} \int_0^L \rho \delta \dot{v} \delta \dot{v} d x = \left[\int_0^L \rho \dot{v} \delta v d x\right]_{t_1}^{t_2}-\int_{t_1}^{t_2} \int_0^L \rho \ddot{v} \delta v d x$

其中第一项为0。

第二项为了消除变分中的二阶导，我们要进行两次分部积分：

$-\int_{t_1}^{t_2}\int_0^L E I \frac{\partial^2 v}{\partial x^2} \delta\left(\frac{\partial^2 v}{\partial x^2}\right) d x = -\left[\int_{t_1}^{t_2} E I \frac{\partial^2 v}{\partial x^2} \delta\left(\frac{\partial v}{\partial x}\right) d t\right]^L_0+\left[\int_{t_1}^{t_2} E I \frac{\partial^3 v}{\partial x^3} \delta v d t\right]^L_0-\int_{t_1}^{t_2} \int_0^L E I \frac{\partial^4 v}{\partial x^4} \delta v d x d t$

第三项对应另外两种情况将分别为：

$\int_{t_1}^{t_2}kv(L,t)\delta v(L,t)$

和

$\int_{t_1}^{t_2}\alpha\frac{\partial v(L,t)}{\partial x}\delta\left(\frac{\partial v(L,t)}{\partial x}\right)dt$

最终合并同类项之后，得到与受力无关的运动方程：

$E I \frac{\partial^h v}{\partial x^4}+\rho s \ddot{v}=0$

和约束条件：

$\begin{align} &-E I \frac{\partial^3 v(0,t)}{\partial x^3} \delta v(0,t) = 0 \Rightarrow v(0,t) = 0 \\& +E I \frac{\partial^2 v(0,t)}{\partial x^2} \delta\left(\frac{\partial v(0,t)}{\partial x}\right)=0\Rightarrow \frac{\partial v(0,t)}{\partial x} = 0 \end{align}$

这两个约束条件和受力无关，以及于受力相关的：

$\begin{align} &\left(E I \frac{\partial^3 v(L,t)}{\partial x^3}+F_0||-kv(L,t)||0\right) \delta v=0\nonumber \\& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow E I \frac{\partial^3 v}{\partial x^3}(L, t)=-F_0||kv(L,t)||0 \end{align}$

$A||B||C$分别代表受恒定外力、受弹簧提供的外力和受力矩作用的情况。最后是关于力矩的：

$\begin{align}(-E I &\frac{\partial^2 v(L,t)}{\partial x^2}-\alpha \frac{\partial v(L,t)}{\partial x}) \delta\left(\frac{\partial v(L,t)}{\partial x}\right) = 0\nonumber \\& \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Rightarrow -E I \frac{\partial^2 v(L,t)}{\partial x^2}=\alpha \frac{\partial v(L,t)}{\partial x} \end{align}$

如果不受力矩，则直接有：

$\frac{\partial^2 v(L,t)}{\partial x^2} = 0$

对应两个受力的情况。