基本简化技术：代数法和卡诺法 Techniques de simplification élémentaires : méthode algébrique et méthode de Karnaugh

代数方法

函数的表达式可以从其真值表中获得：我们搜索真值表中函数等于 1 的行，并在它们之间添加与这些行中的每一行对应的最小项（对于变量的每个组合），如果在真值表的相应行中 a = 1，我们记下变量的名称 a，如果 a = 0，我们记下它的补码 a）。因此，获得的表达式是小项之和。然后可以利用布尔代数的性质获得布尔表达式的简化

以以下真值表为例：

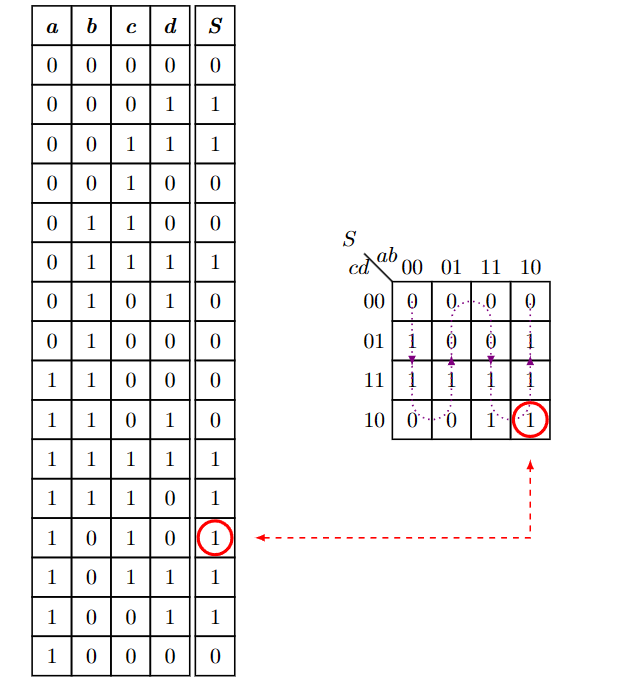
第一个最小项是第二行，\(a,b,c,d\)分别对应\(0,0,0,1\)，由此可以写出第一项为：\(\bar{a} \cdot \bar{b} \cdot \bar{c} \cdot d\)。通过这种方法可以最终写出：

\[ S=\bar{a} \cdot \bar{b} \cdot \bar{c} \cdot d+\bar{a} \cdot \bar{b} \cdot c \cdot d+\bar{a} \cdot b \cdot c \cdot d+a \cdot b \cdot c \cdot d+a \cdot b \cdot c \cdot \bar{d}+a \cdot \bar{b} \cdot c \cdot \bar{d}+a \cdot \bar{b} \cdot c \cdot d+a \cdot \bar{b} \cdot \bar{c} \cdot d \]

然后我们要进行化简：

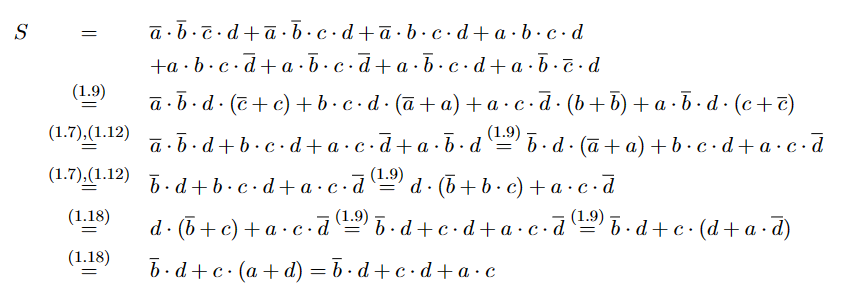
图中公式对应：

\((1.9)\): \(ab+ac = a(b+c)\)
\((1.7)\): \(a\cdot 1 = a\)
\((1.12)\): \(a+\bar a = 1\)
\((1.18)\): \(a+\bar a b = a+b\)

最终得到最简的结果：

\[ S=\bar{b} \cdot d+c \cdot d+a \cdot c \]

卡诺方法 Méthode de Karnaugh

介绍

我们以一个具有8个布尔变量的函数为例，我们将4个变量作为列标签，这对应16列，注意这里使用的是格雷码：

如果我们定义\(\mathcal{E}_x(x \in\{a, b, c, d, \bar{a}, \bar{b}, \bar{c}, \bar{d}\})\)，将所有某个变量k为真对应的列记为\(\mathcal{E}_k\)，为假的列记为\(\mathcal{E}_{\bar k}\)。例如：

\(\mathcal{E}_{\bar{d}}=\{1\} \cup [ 4,5 ] \cup [ 8,9 ] \cup [ 12,13 ] \cup\{16\}\)
\(\mathcal{E}_d=[ 2,3 ] \cup [ 6,7 ] \cup [ 10,11 ] \cup [ 14,15 ]\)

有：\(\mathcal{E}_{\bar{d}}=[ 1,16 ]-\mathcal{E}_d\)

由此，我们可以通过这些元素的交集来表示任何一列或者几列：

\[ \{2\}=[ 2,3 ] \cap([ 1,2 ] \cup [ 7,10 ] \cup [ 15,16 ])=\mathcal{E}_{\bar{a} \cdot \bar{b} \cdot d} \cap \mathcal{E}_{\bar{c}}=\mathcal{E}_{\bar{a} \cdot \bar{b} \cdot \bar{c} \cdot d} \]

更进一步的，我们可以直接用表示每一组框。

随后可以通过使用此方法对卡诺表中 S = 1 的所有框进行分组来确定 S 的简化代数表达式，然后以和的形式表示 S（在意义上逻辑中）术语）对应于这些分组中的每一个的代数表达式。

八行八列的例子

例如，考虑下图中的卡诺表，它表示 8 个布尔变量 a、b、c、d、e、f、g、h 的函数 S。

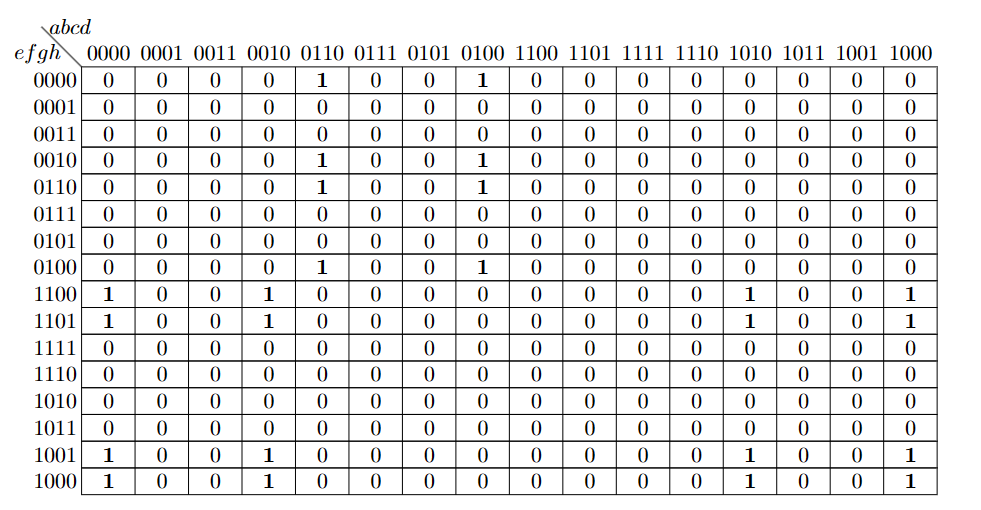
我们首先对这些S = 1的框分组：

第一组包括8个框，对应两个列和四个行的并集，两个列对应3个变量，四个行对应两个变量。两个列与\(c\)无关，因此对应\(\bar a, b, \bar d\) 。四个行与fg无关，因此对应\(\bar e,\bar h\)

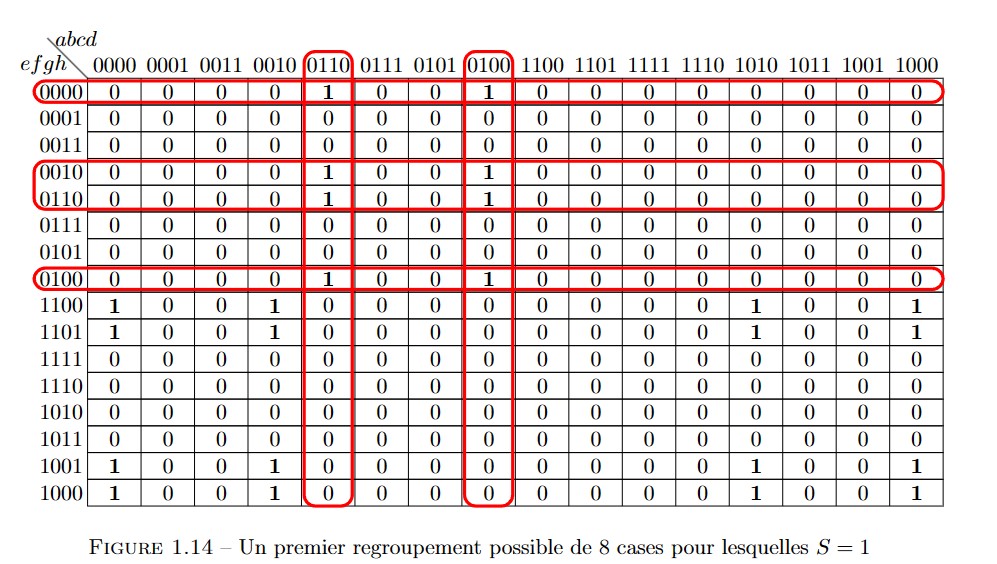
因此对应表达式：\(\bar{a} \cdot b \cdot \bar{d} \cdot \bar{e} \cdot \bar{h}\)
第二组同样包括16个框，包括四个行和四个列

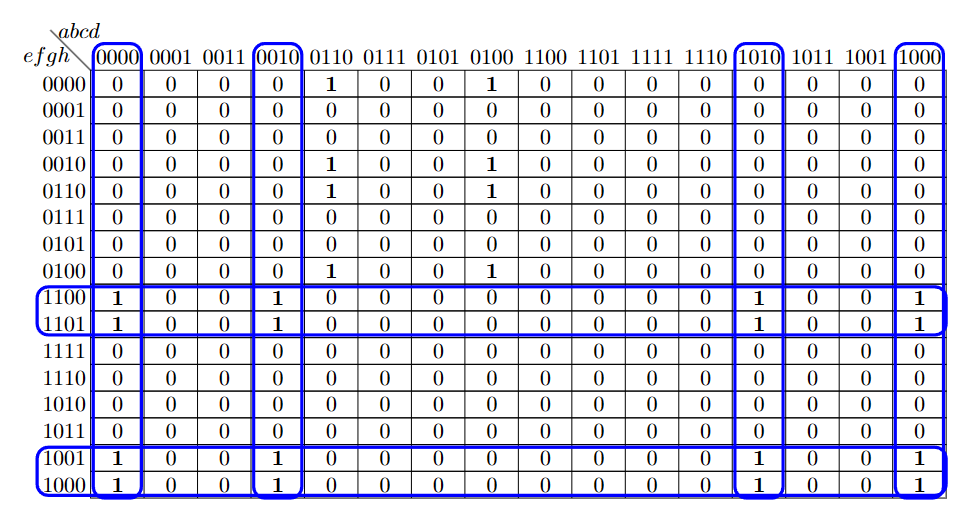
同样的方式可以确定表达式为：\(\bar{b} \cdot \bar{d} \cdot e \cdot \bar{g}\)
最终的表达式为：\(S=\bar{a} \cdot b \cdot \bar{d} \cdot \bar{e} \cdot \bar{h}+\bar{b} \cdot \bar{d} \cdot e \cdot \bar{g}\)

四行四列的例子

普通的

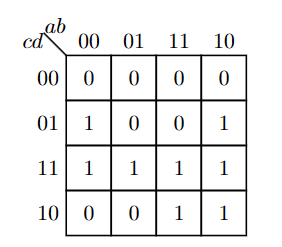
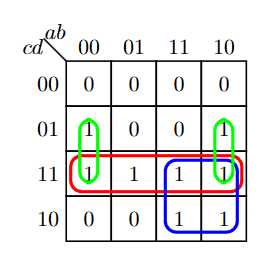
\(S=\bar{b} \cdot d+c \cdot d+a \cdot c\)
\(\begin{aligned} S & =\overline{\bar{c} \cdot \bar{d}+b \cdot \bar{c}+\bar{a} \cdot \bar{d}}=\overline{\bar{c} \cdot \bar{d}} \cdot \overline{b \cdot \bar{c}} \cdot \overline{\bar{a} \cdot \bar{d}}=(c+d) \cdot(\bar{b}+c) \cdot(a+d) \\ & =(c+\bar{b} \cdot d) \cdot(a+d)=a \cdot c+c \cdot d+a \cdot \bar{b} \cdot d+\bar{b} \cdot d=a \cdot c+c \cdot d+\bar{b} \cdot d \end{aligned}\)

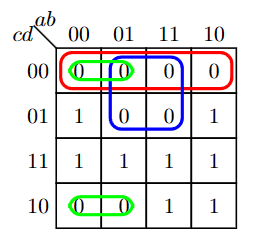
特殊的

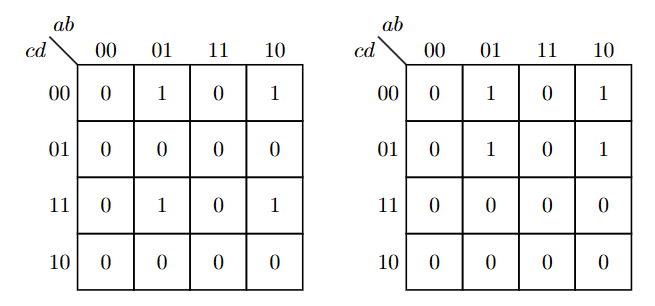
可以看到第一幅图似乎a,b都没有影响，但这是错误的，我们应该注意到a,b不能取到相同的值，因此，应将其表示为：\((a \oplus b)\)。因此第一幅图对应：\(S=(a \oplus b) \cdot(\overline{c \oplus d})\)
第二幅更加简单：\(S=(a \oplus b) \cdot \bar{c}\)