布尔函数规范、真值表和卡诺表 Spécification d’une fonction booléenne, table de vérité et tableau de Karnaugh

布尔函数的规范表达式 Expressions canoniques d’une fonction booléenne

析取范式 forme canonique disjonctive

表示为项的和

$$S=a \cdot b+\bar{a} \cdot \bar{b}$$

我们还要求范式表示为最小项 mineterme 的和: 在每一项中一个变量最多只允许出现一次包括其补码。

合取范式 forme canonique conjonctive

表示为项的乘积

$$S=(a+\bar{b}) \cdot(\bar{a}+b)$$

我们还要求范式表示为最大项 maxtermes的积：在每一项中一个变量最多只允许出现一次包括其补码。

真值表和卡诺表

真值表 Table de vérité

n 个变量的 p 个布尔函数的真值表是一个具有 (n + p) 列（n 列用于输入逻辑变量，p 列用于输出布尔函数）和 2n 行（对应于 2n 种可能的组合）的表输入变量）。

$$\begin{array}{|c|c|c||c|c|}\hline \boldsymbol{a} & \boldsymbol{b} & \boldsymbol{c} & \boldsymbol{S}_{\mathbf{1}} & \boldsymbol{S}_{\mathbf{2}} \\\hline 0 & 0 & 0 & 1 & 0 \\\hline 0 & 0 & 1 & 1 & 0 \\\hline 0 & 1 & 0 & 1 & 1 \\\hline 0 & 1 & 1 & 1 & 0 \\\hline 1 & 0 & 0 & 0 & 0 \\\hline 1 & 0 & 1 & 1 & 1 \\\hline 1 & 1 & 0 & 0 & 0 \\\hline 1 & 1 & 1 & 0 & 1 \\\hline\end{array}$$

真值表可以清楚地突出显示输入变量的组合和输出函数的相应值，并且可以在这些组合和其他数据（例如十进制的相应数字）之间建立对应关系。但当变量过多时，表过长。

卡诺表 Tableau de Karnaugh

卡诺表是一个具有交叉和顺序条目的真值表，在其 2n 个框中（n 是逻辑输入变量的数量）对单个布尔输出函数的不同值进行分组。因此有必要为每个布尔函数写一个卡诺表。该表有 2l 行和 2c 列，其中 l + c = n。

有两种表示形式：

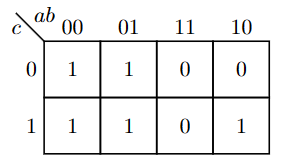
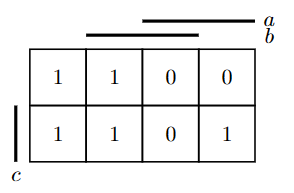
在第二种表示中，存在线代表真，没有线代表假。

卡诺表比真值表更紧凑：p 个卡诺表总共包含 p.2n 个框，而不是相应真值表的 (n + p).2n 个框。然而，正如真值表可以对多个布尔函数的值进行分组一样，也有必要为每个函数创建一个卡诺表。

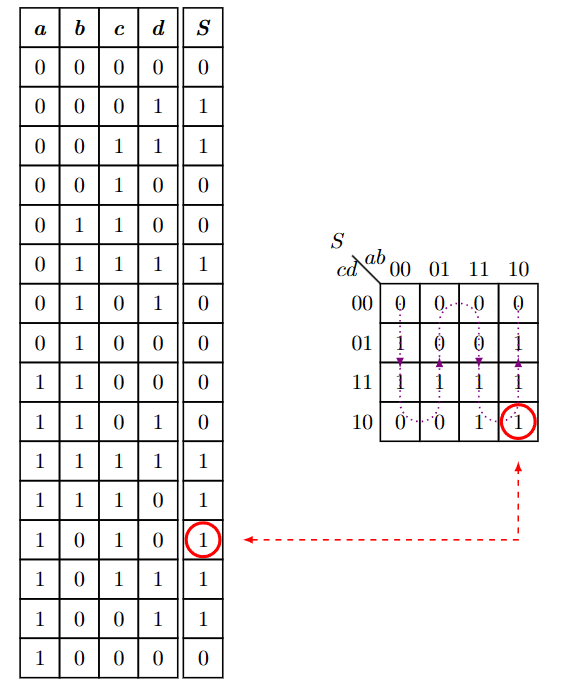
真值表和卡诺表的联系

真值表和卡诺表很容易建立联系，如下图所示：