基本逻辑算符和逻辑门 Opérateurs logiques fondamentaux et portes logiques

一元逻辑运算符

\(f_1\)和\(f_4\)是常量函数 fonctions constantes
\(f_2\)是恒等函数 fonction identité
\(f_3\)是取补函数 fonctions complément

二元逻辑运算符

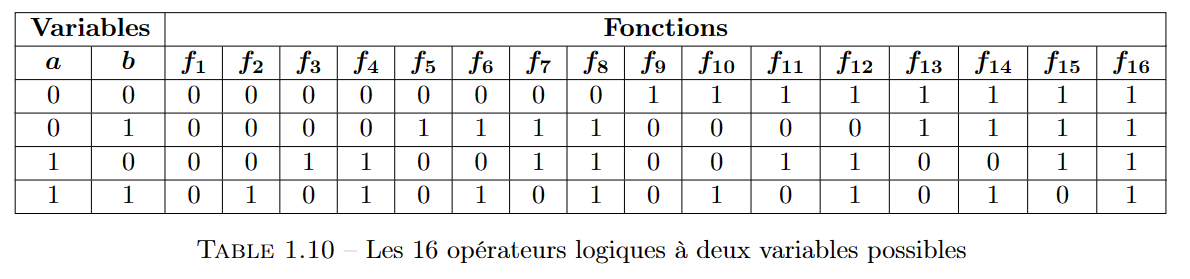
六个函数与一元逻辑运算符相似
- \(f_1\)和\(f_{16}\)是常量函数 fonctions constantes
- \(f_4\)和\(f_6\)是恒等函数 fonctions identité ，前者对于a，后者对于b
- \(f_{13}\)和\(f_{11}\)是取补函数 fonctions complément，前者对于a，后者对于b
有两个函数是逻辑代数运算
- \(f_8\)是或运算 fonction OU inclusif \(\forall(a, b) \in \mathbb{B} \times \mathbb{B}, f_8(a, b)=a+b\)
- \(f_2\)是与运算fonction ET \(\forall(a, b) \in \mathbb{B} \times \mathbb{B}, f_2(a, b)=a \cdot b\)
对于其他函数
- \(f_3\)和\(f_5\)是抑制函数 fonction inhibition/annihilation，前者b抑制a：\(\forall(a, b) \in \mathbb{B} \times \mathbb{B}, f_3(a, b)=a \cdot \bar{b}\)，此时如果\(b = 1\)则无论a的取值，都取0，否则取a的取值。记作：\(f_3(a, b)=a \uparrow b\)
- \(f_7\)是亦或函数 function OU exclusif ou XOR，为真当且仅当\(a,b\)有且仅有一个为真，公式为：\(f_7(a, b)=\bar{a} \cdot b+a \cdot \bar{b}\)，记作\(f_7(a, b)=a \oplus b\)
- \(f_9\)是或非函数 function NON OU ou NOR，为真当且仅当两个输入均为0时，公式为：\(f_9(a, b)=\bar{a} \cdot \bar{b}\)，是与的补
- 函数\(f_{10}\)满足\(∀(a,b)∈B×B,f_{10}(a,b)=\bar a⋅\bar b+a⋅b\)，当且仅当 a=b 时，其值为1，是恒等函数 fonction identité logique, 同时他是亦或函数的补，又称fonction XAND，记为：\(f_{10}(a, b)=a \equiv b\)
- 函数\(f_{12}\)和函数\(f_{14}\)是实质蕴涵函数 fonction implication (de b sur a)，分别为\(f_{12}(a, b)=\bar{a} \cdot \bar{b}+a \cdot \bar{b}+a \cdot b=a+\bar{a} \cdot \bar{b}=a+\bar{b}\)和\(f_{14}(a, b)=\bar{a} \cdot \bar{b}+\bar{a} \cdot b+a \cdot b=\bar{a} \cdot \bar{b}+b=\bar{a}+b\)，分别可以记作：\(f_{12}(a, b)=b \Rightarrow a\)和\(f_{14}(a, b)=a \Rightarrow b\)。以12为例，当b为0时为1，b为1时为a
- 最后一个函数\(f_{15}\)是与非函数fonction NON ET (NAND)，是或函数的补
- 通用基本逻辑运算符是 NOR 和 NAND 运算符。仅使用这两个逻辑运算符之一就可以编写任何布尔表达式。与非和或非函数与或函数和与函数的互补关系被称为 théorèmes de De Morgan . \[ \forall a, b \in \mathbb{B},\left\{\begin{array}{l}\overline{a+b}=\bar{a} \cdot \bar{b} \\\overline{a \cdot b}=\bar{a}+\bar{b}\end{array}\right. \]

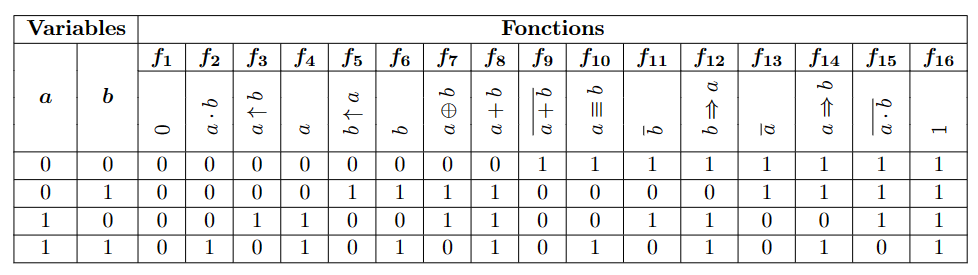
更高维度的逻辑运算符

异或运算符：

\[ \bigoplus_{i=1}^n x_i=1 \]

当且仅当有奇数个\(x_i\)为真。

逻辑门

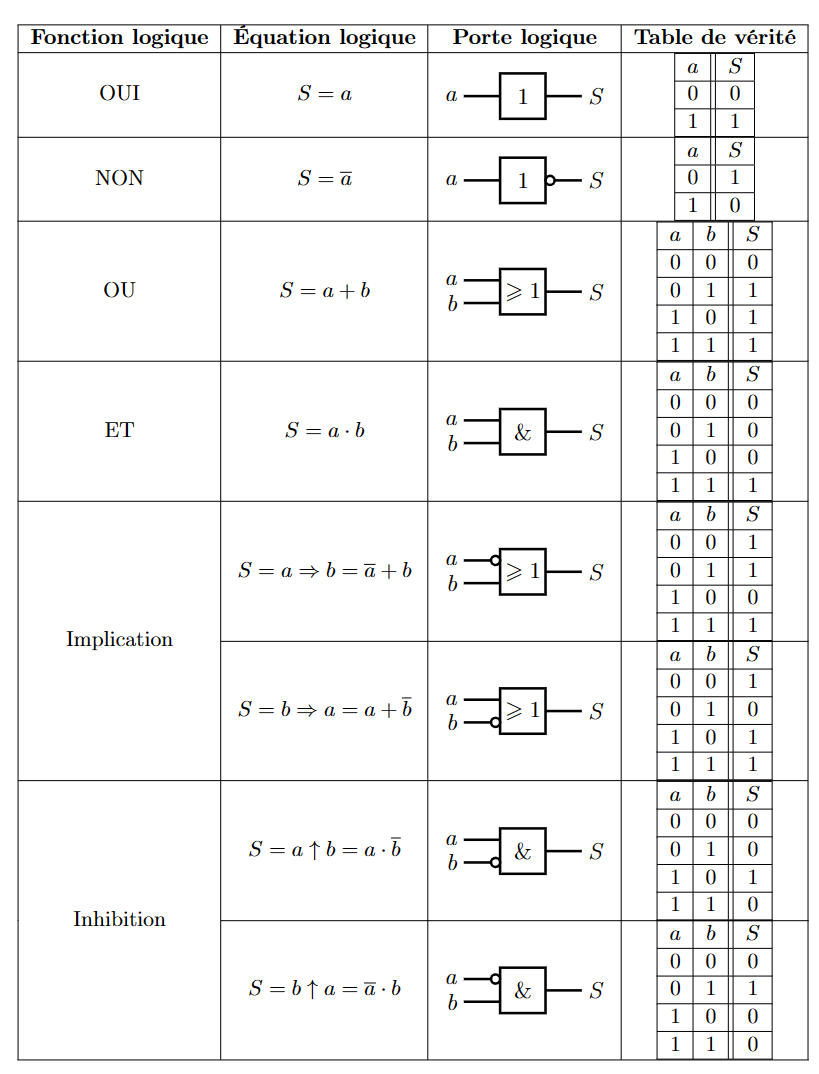
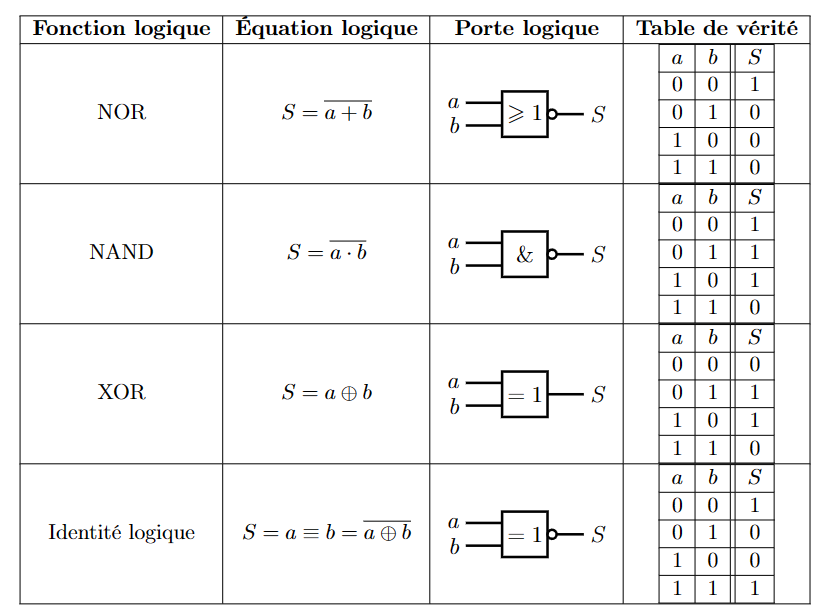
逻辑流程图 Logigramme

逻辑门的关联产生了称为逻辑流程图的图形表示，它可以表示复杂的功能。逻辑流程图用作描述组合系统的工具。

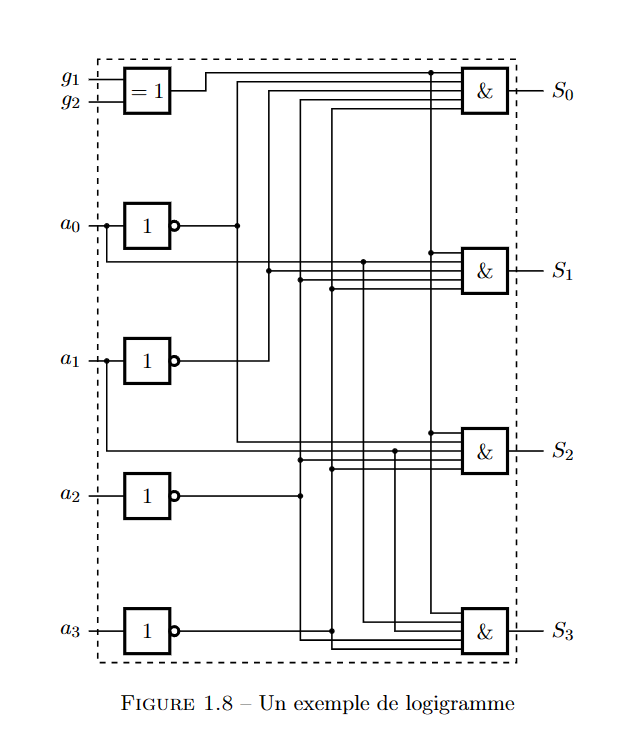
根据逻辑图，我们可以写出以下等式:

\[ \begin{align*}\left\{\begin{aligned}S_0&=(g_1\oplus g_2)\cdot(\bar a_0)\cdot(\bar a_1)\cdot(\bar a_2)\cdot(\bar a_3)\\S_1&=(g_1\oplus g_2)\cdot( a_0)\cdot(\bar a_1)\cdot(\bar a_2)\cdot(\bar a_3)\\S_2&=(g_1\oplus g_2)\cdot(\bar a_0)\cdot( a_1)\cdot(\bar a_2)\cdot(\bar a_3)\\S_3&=(g_1\oplus g_2)\cdot( a_0)\cdot( a_1)\cdot(\bar a_2)\cdot(\bar a_3)\end{aligned}\right.\end{align*} \]