从粒子到波 Des particules aux ondes
从粒子到波 Des particules aux ondes
玻尔轨道模型 Les orbites de Bohr
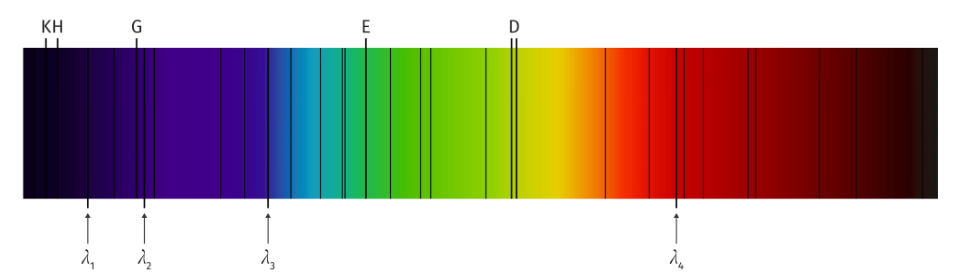
氢原子光谱 Le spectre d’émission de l’hydrogène
当受到5000伏的激发时,氢气变得高度激发,得到一种特殊的光谱。

1885年巴尔默提出了一个经验公式,后来由里茨推广,得到再微弱激发下的波长值:
\[ \frac{1}{\lambda}=R_{\infty}\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \]
其中,\(R_{\infty} \approx 1.097 \times 10^7 \mathrm{~m}^{-1}\)是里德伯格常数(constante de Rydberg)。这是通过观察第一可见发射线分别为红色(0.656μm)、蓝色(0.486μm)、靛蓝(0.434μm)和紫色(0.410μm)来确定的。
尽管经验公式的提出是成功的,离散形式的光谱依然令人困惑。
波尔的原子模型 Le modèle atomique de Bohr
波尔基于卢瑟福提出的原子模型提出了自己的假设:电子围绕原子旋转,且并非所有轨道都是可用的。当他们位于某一特定轨道中运行时,不会发出辐射;当从一个轨道跃迁到另一个轨道时,辐射才会发生。
考虑这个系统的守恒量:
- 角动量:\(L=r \times p\)
- 总能量:\(\varepsilon = T + V\)
- 动能:\(T=\frac{L^2}{2 m r^2}\)
- 势能:\(V=-\frac{e^2}{4 \pi \epsilon_0 r}\)
在某一轨道中,动能不会发生变化:
\[ \frac{L^2}{m r^3}=\frac{e^2}{4 \pi \epsilon_0 r^2} \]
由此需要轨道半径:
\[ r=\frac{L^2 4 \pi \epsilon_0}{m e^2} \]
如此,能量可以表示为角动量的函数:
\[ \varepsilon=-\frac{m}{2 L^2}\left(\frac{e^2}{4 \pi \epsilon_0}\right)^2 \]
因此,根据玻尔的静止轨道模型,轨道修正对应于角动量的变化和随之而来的能量变化:
\[ \varepsilon_1-\varepsilon_2=-\frac{m}{2}\left(\frac{e^2}{4 \pi \epsilon_0}\right)^2\left(\frac{1}{L_1^2}-\frac{1}{L_2^2}\right) \]
我们将这个表达式与巴尔默的经验公式对比,发现电子的角动量必须以一些离散值作为改变。同时,我们可以尝试计算里德伯格常数:
\[ \frac{1}{\lambda}=R_{\infty}\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \Leftrightarrow \hbar \omega=2 \pi \hbar c R_{\infty}\left(\frac{1}{2^2}-\frac{1}{n^2}\right) \]
得到:\(L_n=n \hbar\),\(R_{\infty}=\frac{m}{4 \pi c \hbar^3}\left(\frac{e^2}{4 \pi \epsilon_0}\right)^2\)
应用
- 使用光谱进行图像修复

- 太阳元素分析
德布罗意波粒二象性 La dualité onde-corpuscule de De Broglie
波粒二象性的观念开始形成
在上一章中,以爱因斯坦为首的科学家成功探索了光的波粒二象性。
\[ \begin{array}{ccc}\text { Particules } & & \text { Ondes } \\\text { (quantiques) } & \vec{p}=\hbar \vec{k} & \text { électromagnétiques } \\\varepsilon, \vec{p} & & \omega, \vec{k}\end{array} \]
有质量的粒子所表现波动性也开始得到重视。
德布罗意的研究
德布罗意假设任何的粒子都有波动性,并假设其粒子特性能量和动量与波的特性角频率,波矢和德布罗意波长相联系:
\[ \omega=\varepsilon / \hbar ,\quad k=p / \hbar,\quad \lambda_{\mathrm{dB}}=h / p \]

德布罗意依旧假设电子在轨道上,由于其周期性,\(\lambda_{\mathrm{dB}}=2 \pi \times r / n\)是必要的。
弗兰克和赫兹能量损失实验
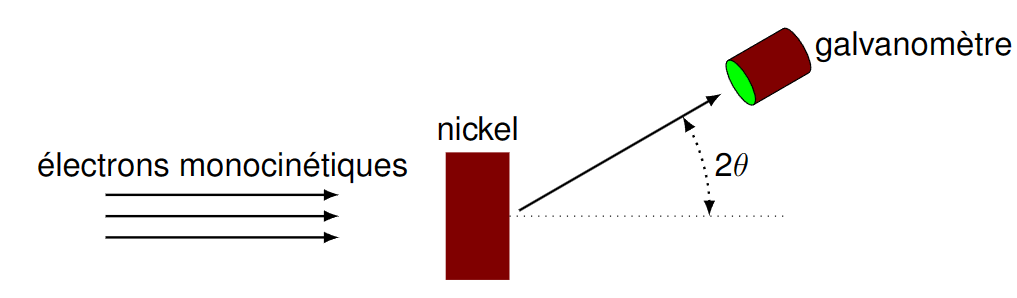
弗兰克-赫兹实验是由德国物理学家詹姆斯·弗兰克和古斯塔夫·赫兹于1914年进行的,他们利用这个实验验证了玻尔模型中关于原子能级的假设。
实验中,电子被加速以获得足够的能量去撞击氩原子。如果电子能量足够让氩原子从基态跃迁到激发态,那么在碰撞过程中电子将损失特定的能量。
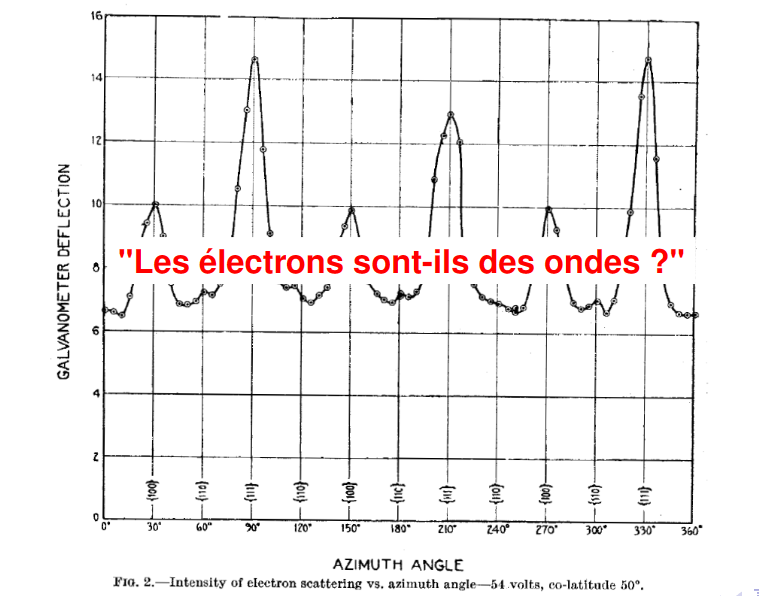
观察到,在特定的加速电压下,电子流经过氩原子后其动能出现特定的损失,这表明它们确实失去了特定的能量给氩原子,使其达到了一个高能级的激发态。这一结果直接支持了玻尔的原子模型,并且为原子能级的量子化提供了直接证据。



