从波到粒子 Des ondes aux particules
从波到粒子 Des ondes aux particules
十九世纪末的物理
这种观点似乎已经传开了,在几年内,所有伟大的物理常数都将被近似估计出来,而留给科学工作者的唯一任务就是将这些度量值更加精确。
现在物理学没有什么新鲜事可谈。剩下的就是越来越精确的测量。
本章将解释科学界是如何在一系列反直觉的实验结果的基础上发明光子的概念的。
黑体辐射光谱 Le spectre de rayonnement du corps noir
每一个温度达到T的物理物体都会辐射出电磁波。人们认为这是由于热量加速了带电粒子的运动,产生了随机非简谐运动,从而产生了电磁波。如此,观察到的辐射光谱应该是连续的。
黑体 corp noir
黑体是完全吸收体,它们吸收所有的电磁辐射而不反射任何电磁辐射,所有的能量都转化为电磁辐射被释放出,而黑体本身处于热平衡状态。
如此,黑体辐射光谱仅取决于热平衡温度。
一个简单的例子如下:
早期黑体的研究
实验结论
Stefan注意到单位时间,单位面积发射的能量与温度的四次方成正比:
\[ P=\sigma T^4 \]
其中\(\sigma\)被称为斯特凡-玻尔兹曼常数(Stefan Boltzmann constant),这个值被证明为:\(\sigma=5,67 \cdot 10^{-8} \mathrm{~W} \cdot \mathrm{m}^{-2} \cdot \mathrm{K}^{-4}\)
Wien观察到能量通量最大时,波长随着黑体平衡温度倒数变化而变化,被称为维恩位移定律:
\[ \lambda_{\max } T=\text { const. } \approx 2.9 \mathrm{~mm} \mathrm{~K} \]
根据这个公式,我们可以确定某种颜色的黑体辐射需要温度的数量级。或者根据温度猜测辐射的温度。
单位体积内的模式数 Nombre de modes par unité de volume
根据这些先前的研究,瑞利(Rayleigh)基于电磁驻波对黑体辐射建模。
对于每个维度,驻波存在要求:
\[ n \lambda=2 L \Leftrightarrow k_n=\frac{2 \pi}{\lambda}=n \frac{\pi}{L}, n \in \mathbb{N} \]
对于三维黑体,要求:
\[ n \lambda=2 L \Leftrightarrow k_n=\frac{2 \pi}{\lambda}=n \frac{\pi}{L}, n \in \mathbb{N} \]
不同模数(mode)之间间隔的体积\(\left(\frac{\pi}{L}\right)^3\)。由此,只考虑\(\vec k\)所有分量为正的情况,我们可以计算波矢的模长小于k的情况下,可能的量子态的数量:
\[ N_k=\frac{1}{8} \frac{(4 / 3) \pi k^3}{(\pi / L)^3}=\frac{k^3 L^3}{6 \pi^2} \]
单位体积内量子态的数量,并用频率\(\nu\)来代替波矢\(k\):
\[ n_k=\frac{N_k}{L^3}=\frac{k^3}{6 \pi^2} \Leftrightarrow n_\nu=\frac{4 \pi}{3 c^3} \nu^3 \Rightarrow \mathrm{d} n_\nu=4 \pi \frac{\nu^2}{c^3} \mathrm{~d} \nu \]
然后考虑磁场和电场各自的两种偏振方向,每种偏振状态都被视为一个独立的模式:
\[ \mathrm{d} N=16 \pi \frac{\nu^2}{c^3} \mathrm{~d} v \]
内能 Énergie thermique
根据能量均分原理(Théorème d’équipartition de l’énergie),每个模式具有\(\frac{k_B T}{2}\)的能量,由此我们得到瑞利-金斯公式:
\[ \mathrm{d} U=\frac{k_B T}{2} \mathrm{~d} N=\frac{8 \pi \nu^2 k_B T}{c^3} \mathrm{~d} \nu=\frac{8 \pi k_B T}{\lambda^4} \mathrm{~d} \lambda \]
与之前的实验结论的对比 Comparaison avec les résultats expérimentaux
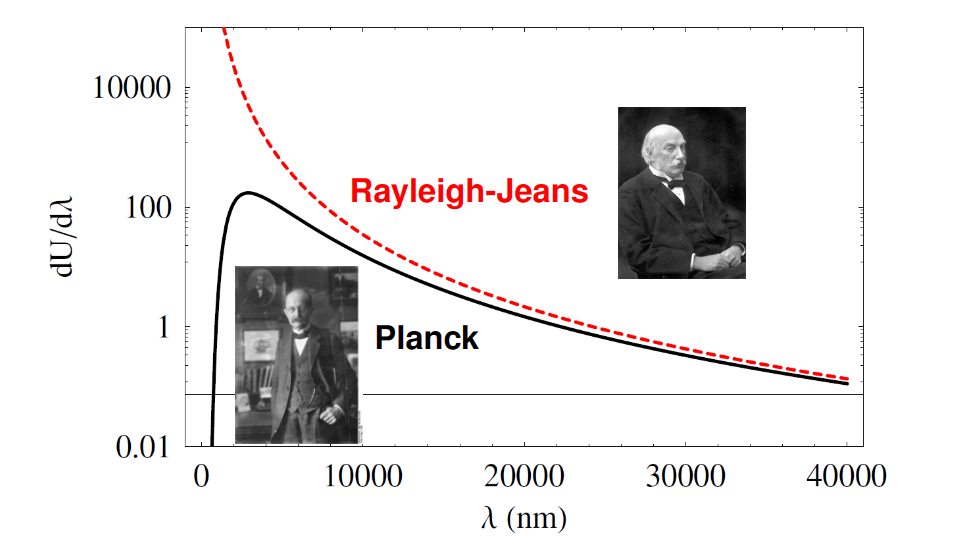
- 在长波长下与实验结果温和较好,但在短波长下,预测的能量密度会趋近于无穷,与实验结果不符合,这被称为紫外灾难(Catastrophe ultraviolette)
- 瑞利-金斯公式预测的辐射能量密度随波长单调递减,这与维恩位移定律不符。
这些问题最终通过普朗克引入了量子假设而解决。
普朗克的研究
1900 年,马克斯·普朗克(Max Planck)确信这纯粹是一个热力学问题,因此承担了解决他认为的这一时期物理学关键点之一的任务,特别是解决微观现象的宏观表现。
普朗克认为模式数的计算没有错误,错误在于我们应该更加精确的计算内能。
玻尔兹曼(Boltzmann)分布
玻尔兹曼分布描述了一个系统在热平衡状态,各个能量级上粒子数的概率分布。
\[ P(\varepsilon)=\frac{e^{-\varepsilon / k_B T}}{\int_0^{+\infty} e^{-\varepsilon / k_B T} \mathrm{~d} \varepsilon} \]
其中,\(ε\) 是粒子的能量,\(k_B\) 是玻尔兹曼常数,\(T\) 是温度。这个公式的分母是一个归一化因子,保证所有能量级上的概率之和为\(1\)。
平均能量 énergie moyenne
根据玻尔兹曼分布,可以直接计算能量的期望值:
\[ \langle\varepsilon\rangle_T=\frac{\int_0^{+\infty} \varepsilon e^{-\varepsilon / k_B T} \mathrm{~d} \varepsilon}{\int_0^{+\infty} e^{-\varepsilon / k_B T} \mathrm{~d} \varepsilon}\rightarrow k_B T \]
在高温极限(即,\(k_BT>>ε\))下,这个公式可以简化为\(⟨ε⟩_T=k_BT\),这就是能量均分定理的结果。
为了补偿短波长时出现的能量发散,我们避免使用连续的积分,而是认为每个连续值之间存在一个最小的间隔\(\Delta \varepsilon=h v\),以避免能量的发散:
\[ \langle\varepsilon\rangle_T=\frac{\sum_{n=0}^{+\infty} n \Delta \varepsilon e^{-n \Delta \varepsilon / k_B T} \Delta \varepsilon}{\sum_{n=0}^{+\infty} e^{-n \Delta \varepsilon / k_B T} \Delta \varepsilon} \]
在较低频率下,\(\Delta \varepsilon=h v\)较小,可以认为连续;但在较高频率下,间隔是不可忽略的。
根据上提示,计算:
\[ \sum_{n=0}^{+\infty} n x^n=x \sum_{n=1}^{+\infty} n x^{n-1}=x \frac{\partial}{\partial x} \sum_{n=0}^{+\infty} x^n=\frac{x}{(1-x)^2} \]
另一方面:
\[ \sum_{n=0}^{+\infty} n e^{-n h \nu / k_B T}=\frac{k_B T^2}{h \nu} \frac{\partial}{\partial T} \sum_{n=0}^{+\infty} e^{-n h \nu / k_B T}=\frac{e^{-h \nu / k_B T}}{\left(1-e^{-h \nu / k_B T}\right)^2} \]
得到:
\[ \langle\epsilon\rangle_T=\frac{h \nu}{e^{h \nu /\left(k_B T\right)}-1} \]
内能 Énergie thermique
上一步计算的平均能量是每个模式具有的能量,由此得到在单位体积内的内能:
\[ dU = \langle\epsilon\rangle_T\times dN = h \nu \frac{1}{e^{h \nu / k_B T}-1} \times 8 \pi \frac{\nu^2}{c^3} \mathrm{~d} \nu \]
转化为以波长作为变量的公式:
\[ d U=\frac{8 \pi h c}{\lambda^5} \frac{1}{e^{h c /\left(\lambda k_B T\right)}-1} d \lambda \]
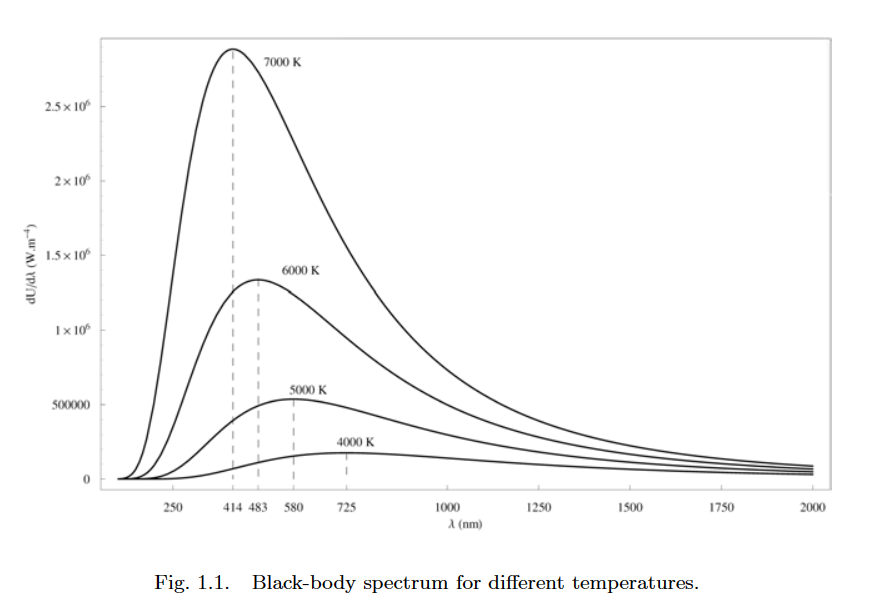
*韦恩位移定理的推导
在短波长时,内能近似为:
\[ d U \approx \frac{8 \pi h c}{\lambda^5} e^{-h c /\left(\lambda k_B T\right)} d \lambda \]
当\(\frac{d^2 U}{d \lambda^2}=0\)时,取\(\frac{\mathrm{d} U}{\mathrm{~d} \lambda}\)最大值:
\[ \frac{d^2 U}{d \lambda^2}=\frac{8 \pi h c e^{-h c /\left(\lambda k_B T\right)}}{\lambda^5}\left(5-\frac{h c}{\lambda k_B T}\right) = 0 \]
得到:
\[ \lambda_{\max } T \approx \frac{h c}{5 k_B} \]
由此得到的常数与实验结果非常相近。
应用
更加详细的内容参见《Application-Driven Quantum and Statistical Physics》一书的\(1.1.1\)
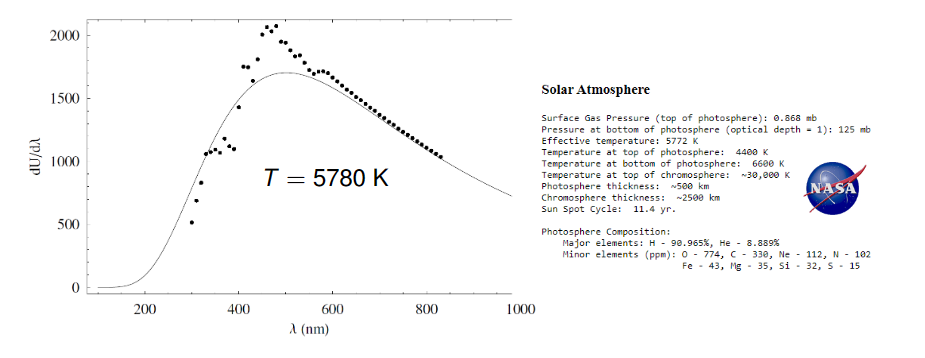
太阳光谱 spectre du Soleil
根据太阳光谱可以推测太阳的有效温度(effective temperature)
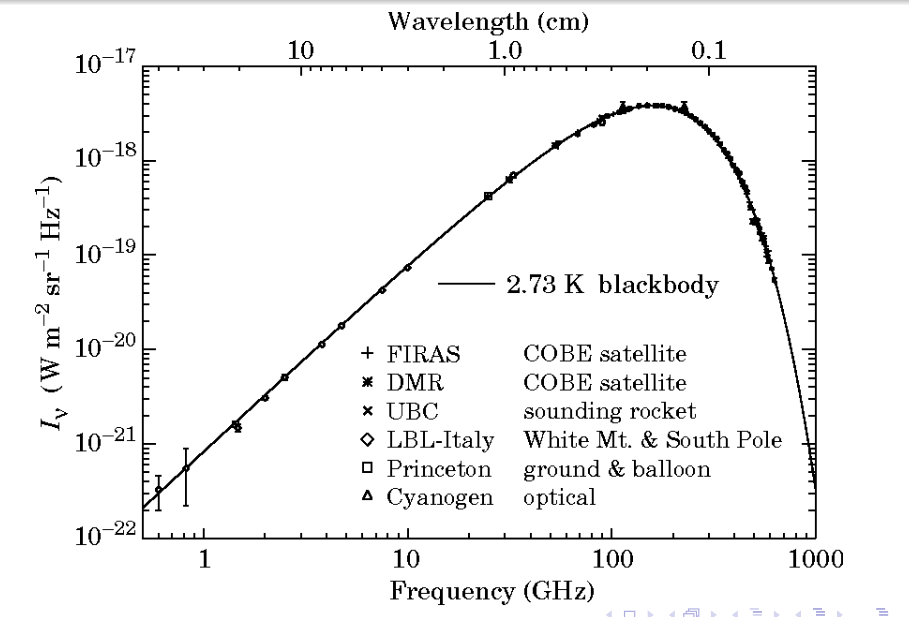
宇宙微波背景 fond diffus cosmologique
频率相关的光电效应 L'effet photoélectrique dépendant de la fréquence
早期实验
哈尔瓦赫斯的光电效应实验:在赫兹的通信的第二年,哈尔瓦赫斯观察到,当一个电荷带电的锌板暴露在弧灯或白炽镁灯泡的紫外光下时,它连接到金箔电子计的放电速度会更快。
J.J. Thomson的理论:Thomson提出,光电效应与阴极射线中观察到的现象没有区别,即在强静电场作用下,导体会发射电子。他基于Maxwell的描述,发展了一种理论,认为入射波携带的电场会诱导电荷的强迫振荡,振荡的幅度与辐射场成正比。因此,被逐出的电子的数量和速度应随波的强度增加而增加。
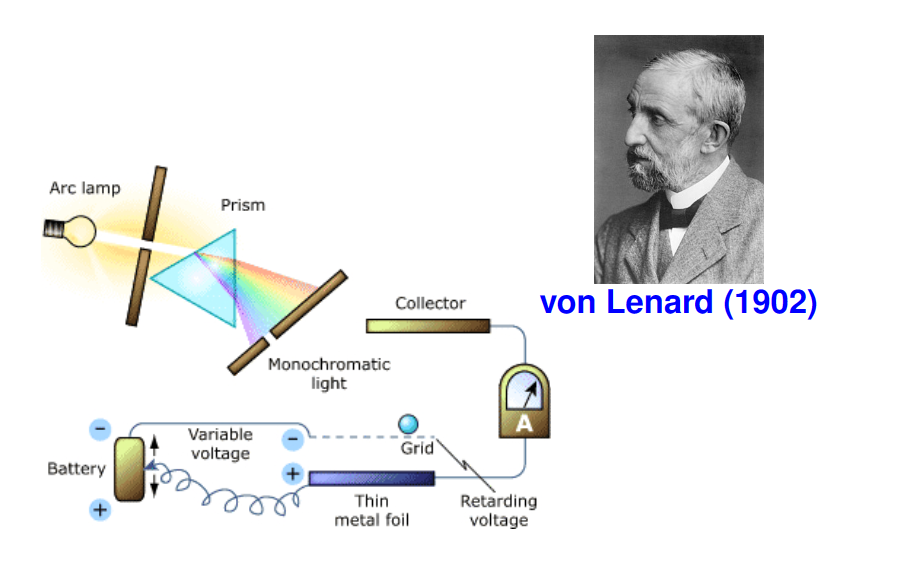
Lenard的实验:1902年,Lenard进行了一个实验,推翻了旧的光-物质相互作用理论。 实验发现,增加光强度会增加电子的数量,但对它们的动能没有可检测的影响。 由于他的灯的功率优势,Lenard可以插入一个光栅,它允许对入射的长波和短波电磁辐射进行定性分离。他的测量结果毫无疑问地显示,出射电子随着频率的增加而加速,而当频率低于一定程度,则不会有出射电子。
爱因斯坦的解释 Explication de Einstein
爱因斯坦放弃了由波携带的电场对电子施加力的观点,坚决采取了能量转移的观点。
他根据普朗克的模型,提出电磁波能量,传递给金属板中的电子,与频率ν成正比,即:
\[ \varepsilon=h \nu=\hbar \omega \]
因此,能量守恒定律要求,被逐出电子的动能是它们吸收的电磁能量\(hν\)与它们用来逃离阴极中原子核吸引势能的能量之差。这个能量被称为功函数,用\(W\)表示。因此,被逐出电子的动能为:
\[ k=hν−W \]
康普顿:测量电子速度 Compton mesure la vitesse des électrons
爱因斯坦重回光粒子
在提出广电效应之后,爱因斯坦产生了光粒子的倾向,正如几个世纪之前牛顿的思想。为此,他在1917年扩展了他的思想,将光子的粒子假设和电磁波假设建立起联系。
对于一个电子,他应该具有量p,使得其动能为\(ε = pc\)。与光电效应得到的电子能量\(\varepsilon=h \nu = \frac{ckh}{2\pi}\)相联系可以得到:
\[ p=\hbar k, \hbar=h / 2 \pi \]
其中,\(\hbar\)被常委约化普朗克常数(Planck reduced constant)。
康普顿散射 Diffusion Compton
康普顿散射实验通过机械守恒定律的光子-电子碰撞证明了光子的粒子性质,可能的“波粒二象性”的想法铺平了道路。

A. H. Compton观察到从石墨靶散射的X射线束的波长增加。在1923年,他将这种现象归因于光子与靶中的电子的非弹性碰撞,即能量转移。根据爱因斯坦的模型,能量和动量守恒可以写为:
\[ \begin{aligned} h \nu_1+\varepsilon_i & =h \nu_2+\varepsilon_f \\ p_1+p_i & =p_2+p_f \end{aligned} \]
其中, \(\nu_1\) 和 \(\nu_2\) 是入射光子和散射光子的频率, \(\varepsilon_i\) 和 \(\varepsilon_f\) 是电子的初始和最终能量, \(p_1\) 和 \(p_2\) 是光子的初始和最终动量, \(p_i\) 和 \(p_f\) 是电子的初始和最终动量。
假设电子初始状态为静止,其初始动量可以认为是0,其初始的能量使用其静止质量计算\(\varepsilon_i=m_e c^2\)。电子的出射的总能量为\(\varepsilon_f=\sqrt{p_f^2 c^2+m_e^2 c^4}\)。
光子的能量和动量可以使用\(p=h \nu / c \text { and } \varepsilon=h \nu\)计算。
假设出射夹角为\(2 \theta\),可以得到能量守恒:
\[ \left[\frac{h}{c}\left(\nu_1-\nu_2\right)+m_e c\right]^2=\frac{h^2}{c^2}\left(\nu_1^2+\nu_2^2-2 \nu_1 \nu_2 \cos 2 \theta\right)+m_e^2 c^2 \]
被简化为:
\[ \nu_1-\nu_2=2 \frac{h \nu_1 \nu_2}{m_e c^2} \sin ^2 \theta \]
\[ \lambda_2-\lambda_1=2 \frac{h c}{m_e c^2} \sin ^2 \theta \]
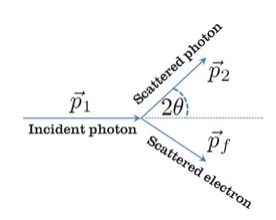
最大波长偏移应该向后反弹,即在\(2\theta = \pi\)时取到,此时有:
\[ \lambda_c=h c /\left(m_e c^2\right) \approx 2.42 \times 10^{-12} \mathrm{~m} \]
是对应于在 90° 散射角处观察到的光子的波长偏移。



