记数系统和编码 Systèmes de numération et codes associés

编码 code

• 编码是一组数字chiffre、字母lettre、单词mot等与某些符号（可能具有相同性质或任何其他性质）之间的双射对应关系。
• 当与数字系统直接关联时，编码被称为加权pondéré编码，因此可以直接对编码表达式执行经典算术操作。

记数系统 Systèmes de numération

基和基数 base et clé

记数系统的基本元素是其基base ，是一组可用来表示任何数值x的数组，其中的数字被称为比重poid

$$\left(\ldots, N^{-n}, N^{-(n-1)}, \ldots, N^{-1}, N^0, N^1, \ldots, N^{p-1}, N^p, \ldots\right), n, p \in \mathbb{N}^*$$

基是由一个自然数N和其幂组成，被称为基数clé

如果我们只对整数感兴趣，可以将其定义为：

$$\left(N^0, N^1, \ldots, N^{p-1}, N^p, \ldots\right), p \in \mathbb{N}^*$$

由此，我们可以将任何一个整数表示为：

$$(X)_N=\left(a_p a_{p-1} \ldots a_1 a_0\right)_N=a_p N^p+a_{p-1} N^{p-1}+\cdots+a_1 N^1+a_0 N^0,$$

其中$a_i$被称为数字digit 。

🦜 如在十进制系统`système décimal`中，$285=(285)_{10}=2.10^2+8.10^1+5.10^0$，其中基数为10，基为$\left(10^0, 10^1, \ldots, 10^{p-1}, 10^p, \ldots\right), p \in \mathbb{N}^*$，2，8，5分别为比重0，1，2的数字

二进制系统和二进制编码 Système binaire et codes binaires

二进制系统 Système binaire

二进制系统是一个基数为2的加权数字系统。

$$(1001)_2=1.2^3+0.2^2+0.2^1+1.2^0;(1001)_2=(9)_{10}$$

比特和字节（八重奏） bit et octet

• 二进制系统的数字被称为比特bit from binary digit
• 八个比特被称为一个字节octet

$$\begin{aligned} & 1 \mathrm{ko}(\text { kilo octet })=2^{10} \mathrm{o}=1024 \mathrm{o} \\ & 1 \mathrm{Mo}(\text { méga octet })=2^{10} \mathrm{ko}=1024 \mathrm{ko}=1048576 \mathrm{o}, \\ & 1 \text { Go }(\text { giga octet })=2^{10} \mathrm{Mo}=1024 \mathrm{Mo}=1048576 \mathrm{ko}=1073741824 \mathrm{o} \end{aligned}$$

• 如果我们将1024近似为1000，则有

$$\begin{aligned}& 1 \text { ko }=10^3 \text { o et } 2^{10} \mathrm{o}=1 \text { Kio (kibioctet), } \\& 1 \mathrm{Mo}=10^6 \text { o et } 2^{20} \mathrm{o}=1 \text { Mio (mébioctet), } \\& 1 \text { Go }=10^9 \text { o et } 2^{30} \mathrm{o}=1 \text { Gio (gibioctet), }\end{aligned}$$

自然二进制编码（纯二进制数） Code binaire naturel ou binaire pur

自然二进制编码建立起二进制编码与十进制编码的联系

$$\begin{array}{|c|c|} \hline \begin{array}{c} \text { Nombre en } \\ \text { base décimale } \end{array} & \begin{array}{c} \text { Code binaire naturel } \\ \left(a_3 a_2 a_1 a_0\right)_2=a_3 \cdot 2^3+a_2 \cdot 2^2+a_1 \cdot 2^1+a_0 \cdot 2^0 \end{array} \\ \hline 0 & 0000 \\ \hline 1 & 0001 \\ \hline 2 & 0010 \\ \hline 3 & 0011 \\ \hline 4 & 0100 \\ \hline 5 & 0101 \\ \hline 6 & 0110 \\ \hline 7 & 0111 \\ \hline 8 & 1000 \\ \hline 9 & 1001 \\ \hline 10 & 1010 \\ \hline 11 & 1011 \\ \hline 12 & 1100 \\ \hline 13 & 1101 \\ \hline 14 & 1110 \\ \hline 15 & 1111 \\ \hline \end{array}$$

编码某十进制数字所需位数

使用$n$位可以表示所有$0$到$\left(2^n-1\right)$的数字

或者可以使用如下公式计算最小需要的位数。

$$\ln N<\ln \left(2^n\right)=n \ln 2 \Leftrightarrow n>\frac{\ln N}{\ln 2}$$

十进制数字增加时的风险

当从一个十进制数字切换到下一个数字时，可能会发生多个逻辑变量改变状态（例如，在代码0111和1000之间，对应于十进制数字7和8，4个逻辑变量同时改变状态）。多个变量状态的同时变化可能导致技术风险，这意味着多个技术组件必须同时改变状态。

组件将以先验未知的顺序连续改变状态，系统将在短时间内操纵错误数据，但足以考虑错误数据。例如，我们可以在0111和1000之间有以下瞬态代码：

$$0111→1111→1011→1001→1000$$

这意味着系统将同时通过值15、11和9，而不是直接从7传递到8，这可能导致计算错误。

格雷码 Code binaire réfléchi (ou code Gray)

格雷码基于自然二进制码，并消除了其多个变量同时改变的风险。在两个连续十进制数之间，格雷码仅有一个变量会发生变化。

$$\begin{array}{|c|c|c|} \hline \begin{array}{c} \text { Nombre en } \\ \text { base décimale } \end{array} & \begin{array}{c} \text { Code binaire } \\ \text { naturel } \end{array} & \begin{array}{c} \text { Code binaire } \\ \text { réfléchi } \end{array} \\ \hline 0 & 0000 & 0000 \\ \hline 1 & 0001 & 0001 \\ \hline \hline 2 & 0010 & 0011 \\ \hline 3 & 0011 & 0010 \\ \hline \hline 4 & 0100 & 0110 \\ \hline 5 & 0101 & 0111 \\ \hline 6 & 0110 & 0101 \\ \hline 7 & 0111 & 0100 \\ \hline \hline 8 & 1000 & 1100 \\ \hline 9 & 1001 & 1101 \\ \hline 10 & 1010 & 1111 \\ \hline 11 & 1011 & 1110 \\ \hline 12 & 1100 & 1010 \\ \hline 13 & 1101 & 1011 \\ \hline 14 & 1110 & 1001 \\ \hline 15 & 1111 & 1000 \\ \hline \end{array}$$

以二进制为0值的格雷码为第零项，第一项改变最右边的位元，第二项改变右起第一个为1的位元的左边位元，第三、四项方法同第一、二项，如此反复，即可排列出n个位元的格雷码

• 0和1的编码不发生变化

格雷码和普通的二进制码可以通过公式：$\mathrm{Bn}=\mathrm{Gn} ; \quad \mathrm{Bi}-1=\mathrm{Bi} \wedge \mathrm{Gi}-1 ; \quad(\mathrm{i}=1,2, \mathrm{n}-1 ;)$转换，如下：

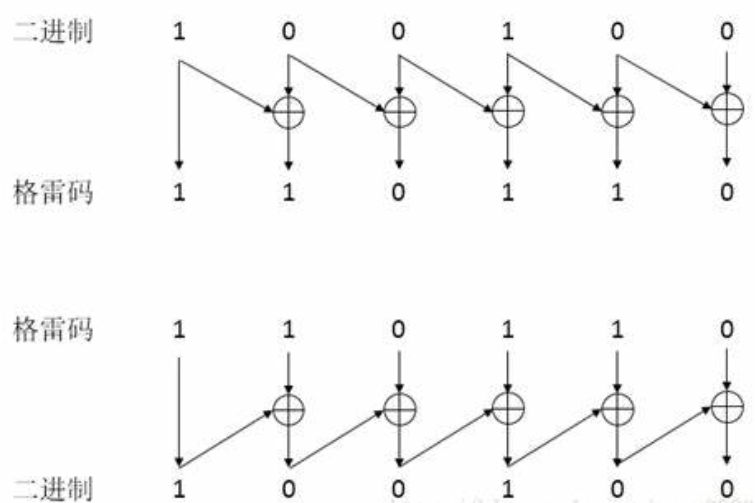
尽管格雷码解决了多个变量同时改变的问题，但他不再是一个加权编码。

BCD码（二-十进制编码） Code DCB (Décimal Codé Binaire)

BCD码对每个十进制数字使用一串单独的二进制编码来存储与表示。并使用这些编码的叠加来表示更大的十进制数。

$$(\underbrace{1}_{(0001)_2} \underbrace{2}_{(0010)_2} \underbrace{5}_{(0101)_2})_{10}=(000100100101)_{\mathrm{DCB}}$$

它具有能够与非常快速的编码/解码算法相关联的优点，并且其主要应用之一是常用的七段显示器。

最常用的BCD编码是8421码，这是一种恒权码，对于其四维，权重分别为8\4\2\1，如：$(0101)_{BCD} = 0\times8+1\times4+0\times1+1\times1 = 5$

条形码和二维码 Code p parmi n

Code p parmi n是一些一系列编码方式，最重要的用途是条码和二维码。能提供$C_n^p=\left(\begin{array}{c}n \p\end{array}\right)$个编码。

阿斯克码 Code ASCII

$$\begin{aligned}&\begin{array}{|c|c|c|c|c|c|}\hline \text { Caractère } & \text { Décimal } & \text { Binaire } & \text { Caractère } & \text { Décimal } & \text { Binaire } \\\hline \mathrm{A} & 65 & 1000001 & \mathrm{~N} & 78 & 1001110 \\\hline \mathrm{B} & 66 & 1000010 & \mathrm{O} & 79 & 1001111 \\\hline \mathrm{C} & 67 & 1000011 & \mathrm{P} & 80 & 1010000 \\\hline \mathrm{D} & 68 & 1000100 & \mathrm{Q} & 81 & 1010001 \\\hline \mathrm{E} & 69 & 1000101 & \mathrm{R} & 82 & 1010010 \\\hline \mathrm{F} & 70 & 1000110 & \mathrm{~S} & 83 & 1010011 \\\hline \mathrm{G} & 71 & 1000111 & \mathrm{~T} & 84 & 1010100 \\\hline \mathrm{H} & 72 & 1001000 & \mathrm{U} & 85 & 1010101 \\\hline \mathrm{I} & 73 & 1001001 & \mathrm{~V} & 86 & 1010110 \\\hline \mathrm{J} & 74 & 1001010 & \mathrm{~W} & 87 & 1010111 \\\hline \mathrm{K} & 75 & 1001011 & \mathrm{X} & 88 & 1011000 \\\hline \mathrm{L} & 76 & 1001100 & \mathrm{Y} & 89 & 1011001 \\\hline \mathrm{M} & 77 & 1001101 & \mathrm{Z} & 90 & 1011010 \\\hline\end{array}\\&\text { TABLE } 1.4 \text { - Code ASCII des } 26 \text { lettres capitales de l'alphabet latin }\end{aligned}$$

十六进制系统和十六进制编码 Système hexadécimal et code hexadécimal

十六进制系统 Système hexadécimal

十六进制系统用于以紧凑的方式表示来自二进制系统的4位组。它在计算机科学中广泛使用，特别是用于指定存储区的地址。

它有16个数字：前10个数字的数字0到9，后6个数字的字母a到f，具有以下对应关系：

$$(\mathrm{A})_{16}=(10)_{10},(\mathrm{~B})_{16}=(11)_{10},(\mathrm{C})_{16}=(12)_{10},(\mathrm{D})_{16}=(13)_{10},(\mathrm{E})_{16}=(14)_{10},(\mathrm{F})_{16}=(15)_{10},$$ $$\begin{array}{|c|c|c|}\hline \begin{array}{c}\text { Valeur en } \\\text { base décimale }\end{array} & \begin{array}{c}\text { Valeur } \\\text { binaire }\end{array} & \begin{array}{c}\text { Valeur } \\\text { hexadécimale }\end{array} \\\hline 0 & 00000 & 0 \\\hline 1 & 00001 & 1 \\\hline 2 & 00010 & 2 \\\hline 3 & 00011 & 3 \\\hline 4 & 00100 & 4 \\\hline 5 & 00101 & 5 \\\hline 6 & 00110 & 6 \\\hline 7 & 00111 & 7 \\\hline 8 & 01000 & 8 \\\hline 9 & 01001 & 9 \\\hline 10 & 01010 & \text { A } \\\hline 11 & 01011 & \text { B } \\\hline 12 & 01100 & \text { C } \\\hline 13 & 01101 & \text { D } \\\hline 14 & 01110 & \text { E } \\\hline 15 & 01111 & \text { F } \\\hline 16 & 10000 & 10 \\\hline 17 & 10001 & 11 \\\hline 18 & 10010 & 12 \\\hline 19 & 10011 & 13 \\\hline 20 & 10100 & 14 \\\hline\end{array}$$

不同进制之间的转换 Changements de système de numération

十进制转N进制

根据定义，X在N进制中可以表示为：

$$\underbrace{X}_{q_0}=\underbrace{\left(a_p N^{p-1}+a_{p-1} N^{p-2}+\cdots+a_2 N+a_1\right)}_{q_1} N+\underbrace{a_0}_{r_0}$$

由此我们可以发现，如果我们使用欧几里得除法除以N，我们将得到其余数$a_0$，而其商可以表示为：

$$\underbrace{a_p N^{p-1}+a_{p-1} N^{p-2}+\cdots+a_2 N+a_1}_{q_1}=\underbrace{\left(a_p N^{p-2}+a_{p-1} N^{p-3}+\cdots+a_3 N+a_2\right)}_{q_2} N+\underbrace{a_1}_{r_1}$$

我们又可以通过继续除以N的方式来获得$a_1$。由此，我们可以得到X在任意进制中的表示。

我们可以使用一种被称为短除法的方式来快速计算，以$(145)_{10}=(10010001)_2$为例。

或者以$(6751){10}=(1 \mathrm{A} 5 \mathrm{F}){16}$为例

N进制转十进制

我们可以使用加权编码的性质快速计算N进制数的十进制表示，以二进制为例：

$$\begin{aligned}(10010001)_2 & =1.2^7+0.2^6+0.2^5+1.2^4+0.2^3+0.2^2+0.2^1+1.2^0 \\& =1 \times 128+0 \times 64+0 \times 32+1 \times 16+0 \times 8+0 \times 4+0 \times 2+1 \times 1 \\& =128+16+1=(145)_{10}\end{aligned}$$

对于十六进制，效果是相同的：

$$\begin{aligned} (1 \mathrm{~A} 5 \mathrm{~F})_{16} & =1.16^3+10.16^2+5.16^1+15.16^0 \\ & =1 \times 4096+10 \times 256+5 \times 16+15 \times 1 \\ & =4096+2560+80+15=(6751)_{10} \end{aligned}$$

二进制转十六进制

十六进制的每一个数字都有唯一的四维二进制表示，我们可以直接替换。

$$(\underbrace{1}_{(0001)_2} \underbrace{\mathrm{A}}_{(1010)_2} \underbrace{5}_{(0101)_2} \underbrace{\mathrm{F}}_{(1111)_2})_{16}=(0001101001011111)_2$$ $$(\underbrace{1}_{(0001)_2} \underbrace{\mathrm{A}}_{(1010)_2} \underbrace{5}_{(0101)_2} \underbrace{\mathrm{F}}_{(1111)_2})_{16}=(0001101001011111)_2$$