Chapter 7 Energy-Based Models 基于能量的模型

当前笔记基本没有涉及对代码的讨论。但这个模型跟我的需求在原理上很契合，在进一步尝试时可能会补充这份笔记。

介绍

基于能量的模型是一类广泛的生成式模型。它借鉴了物理系统建模的关键思想，即事件的概率可以使用玻尔兹曼分布来表示。玻尔兹曼分布是一种将实值能量函数归一化到 \([0,1]\)的特定函数。

Long-au-Vin 的长跑队

我们依然从一个小故事开始说起。

基于能量的模型

基于能量的模型使用玻尔兹曼分布来对真实分布建模：

\[ p(\mathrm{x})=\frac{e^{-E(\mathrm{x})}}{\int_{\widehat{\mathrm{x}} \in \mathrm{X}} e^{-E(\widehat{\mathrm{x}})}} \]

其中\(E(x)\)是能量函数。在训练中，更大区别的观察observation给出更高的能量。

为了完成这个建模，我们需要解决两个主要问题：

  • 即使我们可以根据观察给出能量，我们也并不清楚如何生成一个低能量的观察
  • 我们应该怎么计算分母上的积分

与归一化流不同，我们并不打算找到一种方法能计算出玻尔兹曼分布中的每一项，而是才用近似的方法来避免复杂的运算。

为此，我们使用被称为对比散度contrastive divergence的技术用于训练，郎之万动力学Langevin dynamics的技术用于采样

Energy-Based Models(EMB)

MNIST 数据集

手写数字数据集，过于知名，不再介绍

能量函数

能量函数\(E_\theta(x)\)是一个神经网络结构，其参数被标记为\(\theta\)，可以将输入\(x\)转化为一个标量。特殊的是，这种结构使用了Swish激活函数

Swish激活函数

这种激活函数被定义为：

\[ \begin{aligned}\operatorname{swish}(x)&=x \cdot \operatorname{sigmoid}(x)\\&=\frac{x}{e^{-x}+1}\end{aligned} \]

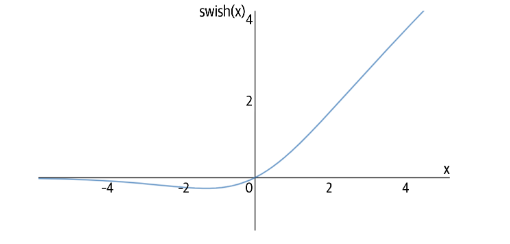
这种函数相当于ReLU激活函数的平滑替代之一，主要用于缓解梯度消失问题。

能量函数层

最终能量函数层被定义为多个卷积和全连接的组合。

1
2
3
4
5
6
7
8
9
10
11
12
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 32, 32, 1)]       0         
 conv2d (Conv2D)             (None, 16, 16, 16)        416       
 conv2d_1 (Conv2D)           (None, 8, 8, 32)          4640      
 conv2d_2 (Conv2D)           (None, 4, 4, 64)          18496     
 conv2d_3 (Conv2D)           (None, 2, 2, 64)          36928     
 flatten (Flatten)           (None, 256)               0         
 dense (Dense)               (None, 64)                16448     
 dense_1 (Dense)             (None, 1)                 65        
=================================================================

使用郎之万动力学进行采样

这种技术很有意思，该技术利用了我们可以计算能量函数相对于其输入的梯度的事实。

如果我们从样本空间中的随机点开始，并在计算梯度的相反方向上迈出一小步，我们将逐渐减小能量函数。如果我们的神经网络训练正确，那么随机噪声应该转换成类似于我们眼前训练集的观察结果的图像。

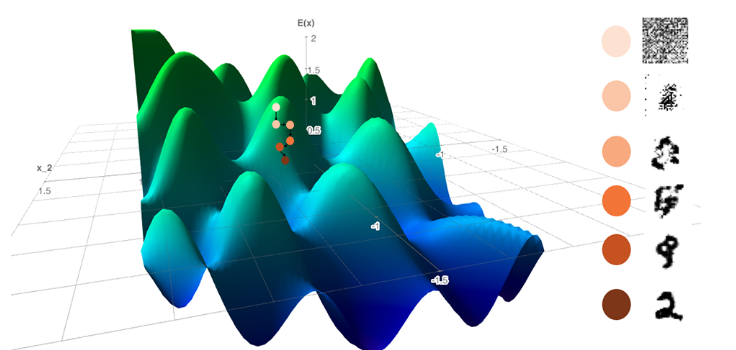
训练神经网络时，我们使用反向传播计算损失函数相对于网络参数（即权重）的梯度。然后我们在负梯度方向上少量更新参数，这样经过多次迭代，我们逐渐最小化损失。

通过朗之万动力学，我们保持神经网络权重固定并计算输出相对于输入的梯度。然后我们在负梯度方向上少量更新输入，以便在多次迭代中，我们逐渐最小化输出（能量得分）。

\[ x^k=x^{k-1}-\eta \nabla_x E_\theta\left(x^{k-1}\right)+\omega \]

  1. 添加噪声：在每个步骤中，首先向输入图像添加正态分布的随机噪声，均值为0，标准差为 noise。然后，使用 tf.clip_by_value 函数将图像的像素值限制在 -1.0 和 1.0 之间。
  2. 计算梯度：接下来，使用 TensorFlow 的 GradientTape 来监视 inp_imgs，并计算模型对 inp_imgs 的输出分数（out_score）。然后，计算 out_score 对 inp_imgs 的梯度（grads），并将梯度值限制在 -0.03 和 0.03 之间。
  3. 更新图像：然后，根据梯度和步长更新 inp_imgs，并再次将像素值限制在 -1.0 和 1.0 之间。

使用对比散度训练

基于对比散度的损失函数

由于能量函数不输出概率，所以我们并不能使用最大似然估计。但我们可以继承这种想法。我们的目的是最小化负似然：

\[ \mathscr{T}=-\mathbb{E}_{x \sim \text { data }}\left[\log p_\theta(\mathbf{x})\right] \]

根据对比散度的一些理论推导，我们可以得到：

\[ \nabla_\theta \mathscr{P}=\mathbb{E}_{x \sim \text { data }}\left[\nabla_\theta E_\theta(\mathbf{x})\right]-\mathbb{E}_{x \sim \text { model }}\left[\nabla_\theta E_\theta(\mathrm{x})\right] \]

我们希望训练模型为真实观察输出大的负能量分数，为生成的假观察输出大的正能量分数，以便这两个极端之间的对比度尽可能大。换句话说，我们可以计算真实样本和假样本能量分数之间的差异，并将其用作我们的损失函数。

同时我们并不真的获得准确的假样本，而是进行若干次郎之万采样程序，运行少量步骤以产生有意义的损失函数。并将这些假的假样本用于下一批的起点，这样我们不需要每次都从噪音开始生成。