Chapter 6 Normalizing Flow Models 标准化流模型

标准化流模型是一种生成模型，用于将一个原始分布通过学习的变换映射到另一个已知的概率分布。它可以把简单的概率密度（比如高斯分布）形式转化成某种复杂的分布形式。所以或许能把标准化流模型称为正态流模型。

本章笔记不包括使用PyTorch的重现，但是本章代码并不困难，未来有兴趣或者会使用这部分知识时会进行复现。

背景故事

我们依然从一个小故事开始讲起，这次故事的主角是雅各布和F.L.O.W.机器

在这个故事中，我们需要关注的有这一长串数字是什么，还有这钟给出了什么信息。

标准化流模型原理

标准化流模型与VAE很像，我们使用解码器模拟一个概率函数\(x = P(z)\)，并使用另一个神经网络编码器，近似这个概率函数的逆\(z = P(z)\) 。简单来说，标准化流模型真的做出了一种可逆神经网络，就像我们先前的故事所述，同一台机器可以把图像变成数字，也可以把数字变成图像。问题是，为什么我们能训练出一个可逆的神经网络。

变量替换

我们考虑一个概率分布\(P_x(x)\)，如图左所示，我们希望将其进行换元，使得起成为一个定义在\(z\in([0,1];[0,1])\)域上的概率分布，如图右所示。我们可以定义一个简单的可逆的变量替换过程，如图中所示。

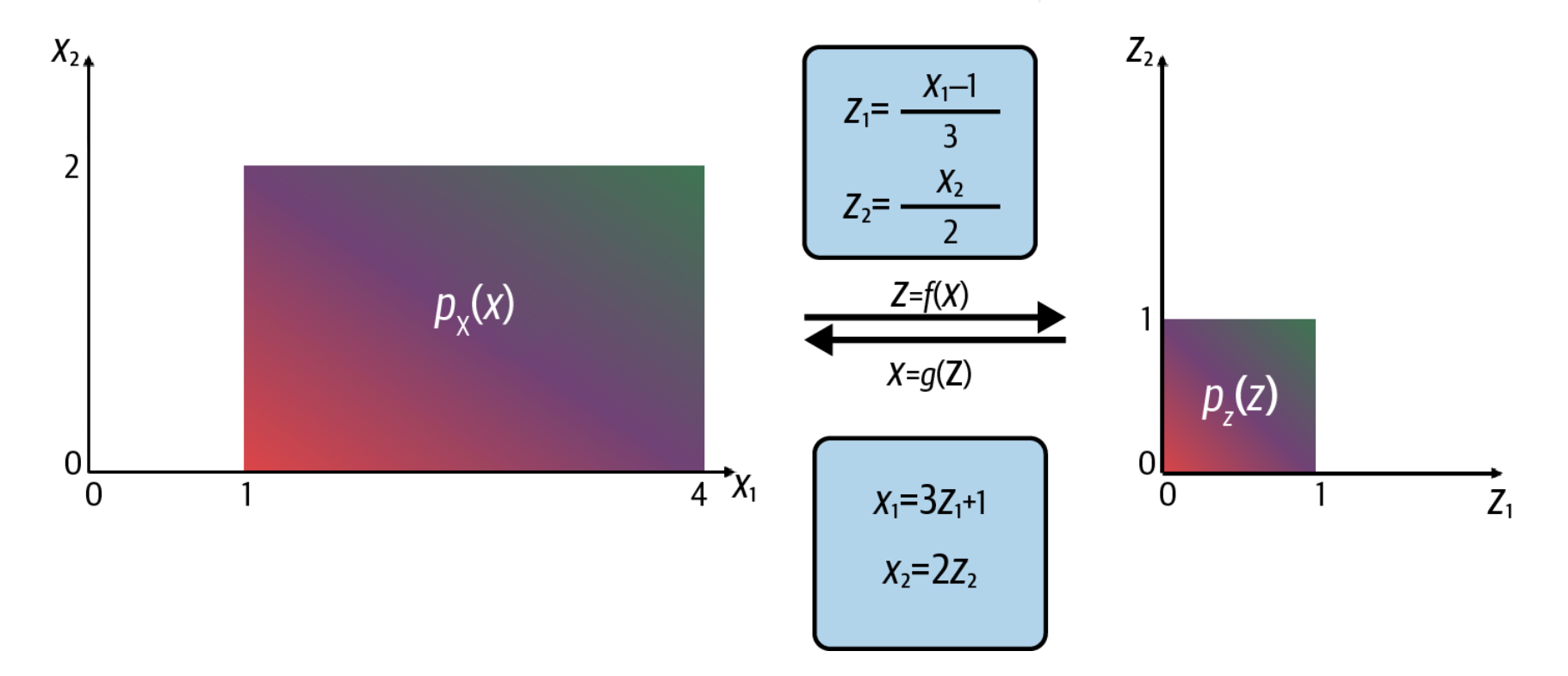
尽管这样的变换非常简单，但是他的面积缩减到了原本的1/6，而强度没有变化，这将会导致换元之后，不再是一个概率函数。

雅可比行列式

雅可比的定义为：

\[ \mathrm{J}=\frac{\partial z}{\partial x}=\left[\begin{array}{ccc}\frac{\partial z_1}{\partial x_1} & \cdots & \frac{\partial z_1}{\partial x_n} \\\ddots & \vdots & \\\frac{\partial z_m}{\partial x_1} & \cdots & \frac{\partial z_m}{\partial x_n}\end{array}\right] \]

雅可比矩阵可以帮助我们定义一个完善的换元方程change of variables equation。

\[ p_X(x)=p_Z(z)\left|\operatorname{det}\left(\frac{\partial z}{\partial x}\right)\right| \]

由此，在理论上，假设我们知道了\(p_X(x)\)，我们知道了\(z\)和\(x\)的关系，从而计算出其雅克比矩阵，我们就能获得另一个分布\(P_z(z)\)，同时，我们获得了一个可逆的转化方式。

但是存在两个问题：

  • 理论上说，z = f(x)这个函数我们是通过神经网络训练而来，而我们不能简单的对这个网络取逆。
  • 而且，计算一个由神经网络定义的函数的雅可比矩阵并非易事

这些问题导致我们在实际建模时需要额外的考虑。

RealNVP

这个神经网络可以将复杂的数据分布转化为简单的高斯分布。他具备了可逆所需的属性和可以简单计算的雅可比矩阵。

两个月亮数据集 *****The Two Moons Dataset*****

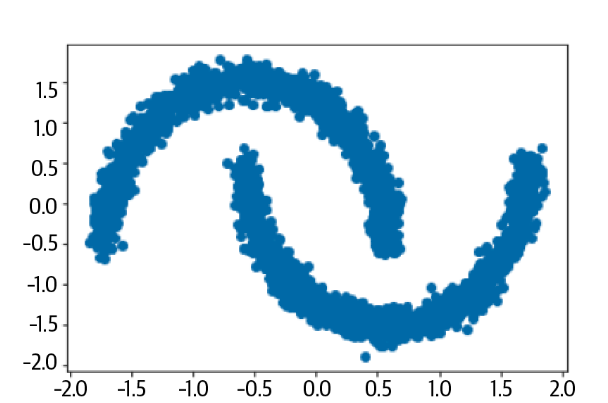
这个数据集是一个形似两个月亮的二维点的嘈杂数据集，比较简单。

耦合层

耦合层为其输入的每个元素生成比例和平移因子。它产生两个与输入大小完全相同的张量，一个用于比例因子，一个用于平移因子。

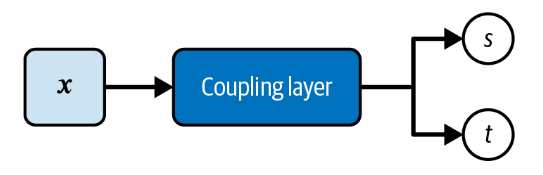
耦合层在实现中可以简单的创建两个的堆叠的全连接层，输入同样的内容，他们会产生两个维度相同的输出，分别作为比例因子和平移因子。

1
2
3
4
5
6
7
8
9
10
11
12
def Coupling(input_dim, coupling_dim, reg):
    input_layer = layers.Input(shape=input_dim)

    s_layer_1 = layers.Dense(coupling_dim, activation="relu", kernel_regularizer=regularizers.l2(reg))(input_layer)
		...
    s_layer_5 = layers.Dense(input_dim, activation="tanh", kernel_regularizer=regularizers.l2(reg))(s_layer_4)

    t_layer_1 = layers.Dense(coupling_dim, activation="relu", kernel_regularizer=regularizers.l2(reg))(input_layer)
		...
    t_layer_5 = layers.Dense(input_dim, activation="linear", kernel_regularizer=regularizers.l2(reg))(t_layer_4)

    return models.Model(inputs=input_layer, outputs=[s_layer_5, t_layer_5])

在这个例子中，两组全连接层的唯一区别就是最终的激活函数。缩放因子的神经网络使用了tanh作为激活函数，而平移层是哦那个了linear作为激活函数。

通过耦合层传递信息

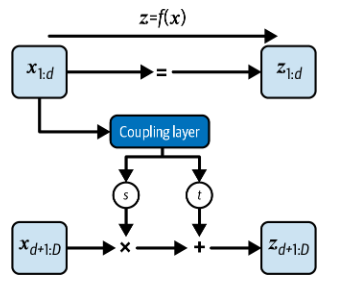
只有数据的前 d 维被馈送到第一耦合层，其余的 D − d 维被完全屏蔽（即设置为零）。在我们的例子中，数据是二维量，因此D = 2，如果d = 1，耦合层将会接收到\(（x_1,0）\)而不是\(（x_1,x_2）\)。

耦合层会输出缩放和平移因子，而这些因子会被作用在原本被隐藏的部分。在我们的例子张，这些因子将会被作用在\(（0,x_2）\)上。

经过这两步操作，我们有\(z\)和\(x\)的关系：

\[ \begin{aligned}&z_{1: d} =x_{1: d} \\&z_{d+1: D} =x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right)\end{aligned} \]

雅可比行列式

这样的处理方法带来的优势可以在其雅可比行列式中体现出来

\[ \frac{\partial z}{\partial x}=\left[\begin{array}{cc}\mathbf{I} & 0 \\\frac{\partial z_{d+1: D}}{\partial x_{1: d}} & \operatorname{diag}\left(\exp \left[s\left(x_{1: d}\right)\right]\right)\end{array}\right] \]

左上角是一个单位阵，左下角是一个对角矩阵。右下角是一个复杂的均值，但是在计算行列式时与这一部分无关。事实上其行列式就等于：

\[ \operatorname{det}(J)=\exp \left[\sum_j s\left(x_{1: d}\right)_j\right] \]

这非常容易计算。

逆运算

我们先前得到\(f(x) = z\)，而其逆也是容易计算的。

\[ \begin{aligned}&z_{1: d} =x_{1: d} \\&z_{d+1: D} =x_{d+1: D} \odot \exp \left(s\left(x_{1: d}\right)\right)+t\left(x_{1: d}\right)\end{aligned} \]

堆叠耦合层

现在我们还剩一个问题，我们怎么更新前d个元素？我们只需要根据两个简单的运算规则就可以找到解决方案

\[ \begin{aligned}\operatorname{det}(\mathrm{A} \cdot \mathrm{B}) & =\operatorname{det}(\mathrm{A}) \operatorname{det}(\mathrm{B}) \\\left(f_b \circ f_a\right)^{-1} & =f_a^{-1} \circ f_b^{-1}\end{aligned} \]

这两个公式指示我们可以堆叠耦合层来解决这个问题，只要我们交替使用掩蔽。

训练RealNVP模型

根据上述原理，我们两个分布的关系：

\[ -\log p_X(x)=-\log p_Z(z)-\log \left|\operatorname{det}\left(\frac{\partial z}{\partial x}\right)\right| \]

在RealNVP中，我们预期的目标输出分布为正态分布。我们可以轻松地从该分布中采样。然后，我们可以通过应用逆过程 g 将从高斯采样的点变换回原始图像域，如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class RealNVP(models.Model):
    def __init__(self, input_dim, coupling_layers, coupling_dim, regularization):
        super(RealNVP, self).__init__()
        self.coupling_layers = coupling_layers
        self.distribution = tfp.distributions.MultivariateNormalDiag(loc=[0.0, 0.0], scale_diag=[1.0, 1.0])
        # 交替的掩蔽
				**self.masks = np.array([[0, 1], [1, 0]] * (coupling_layers // 2), dtype="float32")**
        self.loss_tracker = metrics.Mean(name="loss")
        # 耦合层的列表，这些耦合层都是相同的
				**self.layers_list = [
            Coupling(input_dim, coupling_dim, regularization)
            for i in range(coupling_layers)
        ]**

    def call(self, x, training=True):
				# 这是使用training指标指示我们正向使用网络还是逆向使用网络
        log_det_inv = 0
        direction = 1
        if training:
            direction = -1
        for i in range(self.coupling_layers)[::direction]:
            x_masked = x * self.masks[i]
            reversed_mask = 1 - self.masks[i]
            s, t = self.layers_list[i](x_masked)
            s *= reversed_mask
            t *= reversed_mask
            gate = (direction - 1) / 2
            x = (
                reversed_mask
                * (x * tf.exp(direction * s) + direction * t * tf.exp(gate * s))
                + x_masked
            )
						# 雅可比行列式的对数行列式
            log_det_inv += gate * tf.reduce_sum(s, axis=1)
        return x, log_det_inv

    def log_loss(self, x):
        y, logdet = self(x)
        log_likelihood = self.distribution.log_prob(y) + logdet
        return -tf.reduce_mean(log_likelihood)

    def train_step(self, data):
        with tf.GradientTape() as tape:
            loss = self.log_loss(data)
        g = tape.gradient(loss, self.trainable_variables)
        self.optimizer.apply_gradients(zip(g, self.trainable_variables))
        self.loss_tracker.update_state(loss)
        return {"loss": self.loss_tracker.result()}

损失函数

假设我们的模型表示为 f，输入数据为 x，模型的输出为 z **= f(x)**，那么为了最大化模型分布 \(p_{model}(x)\) 在数据分布 \(p_{data}\) 上的对数似然。损失函数可以表示为:

\[ L(x)=-E_{x \sim p_{\text {data }}}\left[\log p_{\text {model }}(x)\right] \]

根据先前的公式，得到：

\[ \begin{aligned}&L(x)=-E_{x \sim p_{\text {data }}}\left[\log p_{z}(z)+\log \left|\operatorname{det} J_f(x)\right|\right]\\&L(x)=-E_{x \sim p_{\text {data }}}\left[\log p_{\text {base }}(y)\right]+\operatorname{logdet}\end{aligned} \]

即为上述程序中的log_loss

结果分析

一旦模型被训练，我们就可以用它来将训练集转换到潜在空间，或将潜在空间中的采样点转换成接近训练集中数据的信息。正向过程能够转换来自训练的点设置为类似于高斯的分布后向过程可以从高斯分布中采样点，并将它们映射回类似于原始数据的分布