Chapter 3 Variational Autoencoders 自动变分编码器

介绍

2013 年，Diederik P. Kingma 和 Max Welling 发表了一篇论文，为一种称为变分自编码器 (VAE) 的神经网络奠定了基础。

故事

💡 想象一下，你面前的地板上堆满了你所有的衣服——裤子、上衣、鞋子和外套，款式各异。你的造型师布莱恩越来越沮丧，因为他花了很长时间才能找到你需要的物品，因此他制定了一个聪明的计划。他告诉你把你的衣服整理成一个无限高和无限宽的衣柜。当您想要索取特定物品时，您只需告诉布莱恩它的位置，他就会使用他值得信赖的缝纫机从头开始缝制该物品。很快就会发现，您需要将相似的项目彼此靠近放置，以便 Brian 可以仅根据其位置准确地重新创建每个项目。

经过几周的练习，你和布莱恩已经适应了彼此对衣柜布局的理解。现在您可以告诉布莱恩您想要的任何衣服的位置，他可以从头开始准确地缝制它！这给了你一个想法——如果你给布莱恩一个空的衣柜位置，会发生什么？令你惊讶的是，你发现布莱恩能够完全生成以前不存在的新衣服！这个过程并不完美，但你现在有无限的选择来生成新衣服，只需在无限衣柜中选择一个空位置，然后让布莱恩用缝纫机施展他的魔法。

自动编码器

与故事的对应

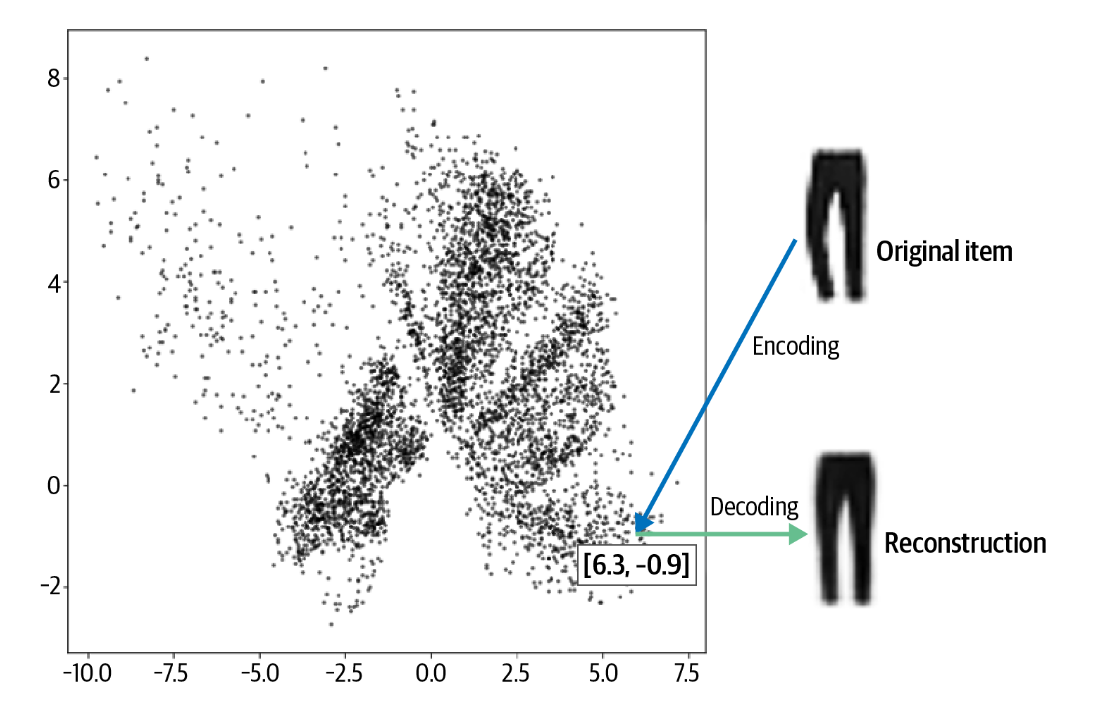
将每件衣服移动到衣柜中的某个位置。这个过程称为编码。布莱恩扮演解码器的角色，在衣柜中找到一个位置并尝试重新创建该物品。这个过程称为解码。

例如，图中的裤子被编码为点 [6.3, –0.9]。该向量也称为嵌入embedding，因为编码器尝试将尽可能多的信息嵌入其中，以便解码器可以产生准确的重建

自动编码器

自动编码器只是一个神经网络，经过训练来执行对项目进行编码和解码的任务，以便该过程的输出尽可能接近原始项目。

Fashion-MNIST 数据集

Fashion-MNIST是一个替代MNIST手写数字集的图像数据集。其涵盖了10种类别的衣物，包括T恤、裤子、套头衫等等。每个类别有7000个训练图像和3000个测试图像。数据集中的每个图像都是28x28的灰度图像。

********************加载数据集********************

from tensorflow.keras import datasets
(x_train,y_train), (x_test,y_test) = datasets.fashion_mnist.load_data()

数据集处理

def preprocess(imgs):
	imgs = imgs.astype("float32") / 255.0
	imgs = np.pad(imgs, ((0, 0), (2, 2), (2, 2)), constant_values=0.0)
	imgs = np.expand_dims(imgs, -1)
	return imgs
x_train = preprocess(x_train)
x_test = preprocess(x_test)

自动编码器架构

自动编码器是一个由两部分组成的神经网络

• 编码器网络，将高维输入数据（例如图像）压缩为低维嵌入向量
• 解码器网络，将给定的嵌入向量解压回原始值域（例如，返回图像）

编码器

编码器在自动编码器中，编码器的工作是获取输入图像并将其映射到潜在空间中的嵌入向量。

encoder_input = layers.Input(
shape=(32, 32, 1), name = "encoder_input"
)
x = layers.Conv2D(32, (3, 3), strides = 2, activation = 'relu', padding="same")(
encoder_input
)
x = layers.Conv2D(64, (3, 3), strides = 2, activation = 'relu', padding="same")(x)
x = layers.Conv2D(128, (3, 3), strides = 2, activation = 'relu', padding="same")(x)
shape_before_flattening = K.int_shape(x)[1:]
x = layers.Flatten()(x)
encoder_output = layers.Dense(2, name="encoder_output")(x)
encoder = models.Model(encoder_input, encoder_output)

转置卷积层

标准卷积层允许我们通过设置 strides = 2 将输入张量的两个维度（高度和宽度）的大小减半。卷积转置层使用与标准卷积层相同的原理（在图像上传递过滤器），但不同之处在于设置 strides = 2 使输入张量在两个维度上的大小加倍。

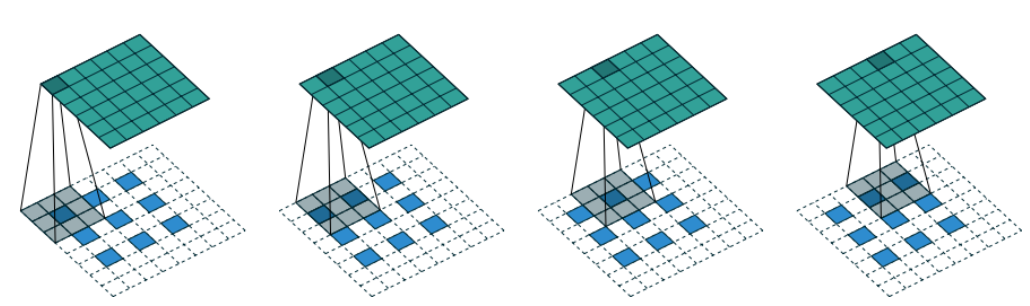
在 Keras 中，**Conv2DTranspose** 层允许我们对张量执行卷积转置操作。通过堆叠这些层，我们可以使用步长 2 逐渐扩大每层的大小，直到回到原始图像尺寸 32 × 32

解码器

decoder_input = layers.Input(shape=(2,), name="decoder_input")
x = layers.Dense(np.prod(shape_before_flattening))(decoder_input)
x = layers.Reshape(shape_before_flattening)(x)
x = layers.Conv2DTranspose(
128, (3, 3), strides=2, activation = 'relu', padding="same"
)(x)
x = layers.Conv2DTranspose(
64, (3, 3), strides=2, activation = 'relu', padding="same"
)(x)
x = layers.Conv2DTranspose(
32, (3, 3), strides=2, activation = 'relu', padding="same"
)(x)
decoder_output = layers.Conv2D(
1,
(3, 3),
strides = 1,
activation="sigmoid",
padding="same",
name="decoder_output"
)(x)
decoder = models.Model(decoder_input, decoder_output)

连接编码器和解码器

autoencoder = Model(encoder_input, decoder(encoder_output))

我们只需要指定自动编码器的输出编码器通过解码器后的输出。

模型训练

选择合适的优化器和损失函数

• 优化器选择常规的Adam优化器
• 损失函数通常选择原始图像和重建图像的各个像素之间的均方根误差（RMSE）或二元交叉熵

autoencoder.compile(optimizer="adam", loss="binary_crossentropy")

均方根误差（RMSE）和二元交叉熵，都是度量预测值和真实值之间差异的方法

• 均方根误差（RMSE）是观测值与真实值之间差异的平方和的平方根。RMSE 对所有类型的预测错误都有相同的权重，无论预测值是高估还是低估真实值。
• 另一方面，二元交叉熵损失函数度量的是预测值和真实值之间的“距离”。二元交叉熵损失函数对预测错误的处理并不对称。如果真实值接近1，模型预测越接近1，损失就越小；反之，如果真实值接近0，模型预测越接近0，损失就越小。这就意味着，如果你的模型对某个值的预测结果过高或过低，那么损失函数的值会明显增加。

这两种损失函数各有优势，选择哪种损失函数应该根据你的具体需求和实验结果来决定。

开始训练

autoencoder.fit(
		x_train,
		x_train,
		epochs=5,
		batch_size=100,
		shuffle=True,
		validation_data=(x_test, x_test),
)

重建图像

使用测试机测试重建图像的能力

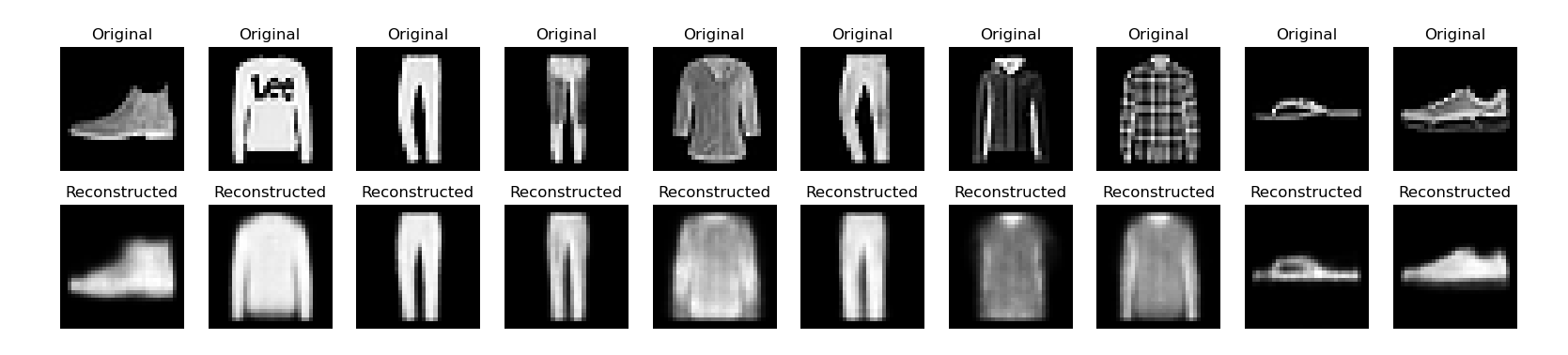
example_images = x_test[:5000]
predictions = autoencoder.predict(example_images)

生成新的图像

我们首先生成获得可能的潜在空间

embeddings = encoder.predict(example_images)
mins, maxs = np.min(embeddings, axis=0), np.max(embeddings, axis=0)
sample = np.random.uniform(mins, maxs, size=(18, 2))

• 我们首先通过编码器，对训练集的数据进行编码以获得可能的潜在空间。
• 然后我们认为采样空间是包含潜在空间的最小矩形。
• 在这个空间内均匀采样，并使用解码器进行预测

由此即可生成新的图像，并绘制：

n = 18  # Number of images to display
plt.figure(figsize=(20, 4))
for i in range(n):
    # Display original images
    # ax = plt.subplot(2, n, i + 1)
    # plt.imshow(example_images[i].reshape(32, 32), cmap='gray')
    # plt.title("Original")
    # plt.axis('off')

    # Display reconstructed images
    ax = plt.subplot(2, n, i + 1 + n)
    plt.imshow(reconstructions[i].reshape(32, 32), cmap='gray')
    plt.title("Reconstructed")
    plt.axis('off')

自动编码器存在的问题

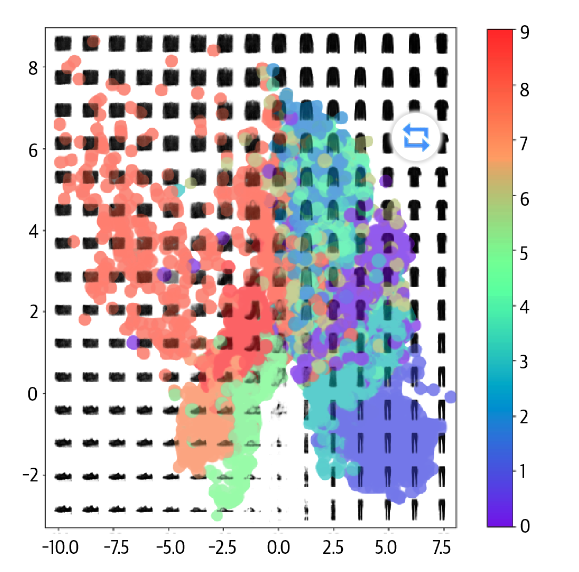
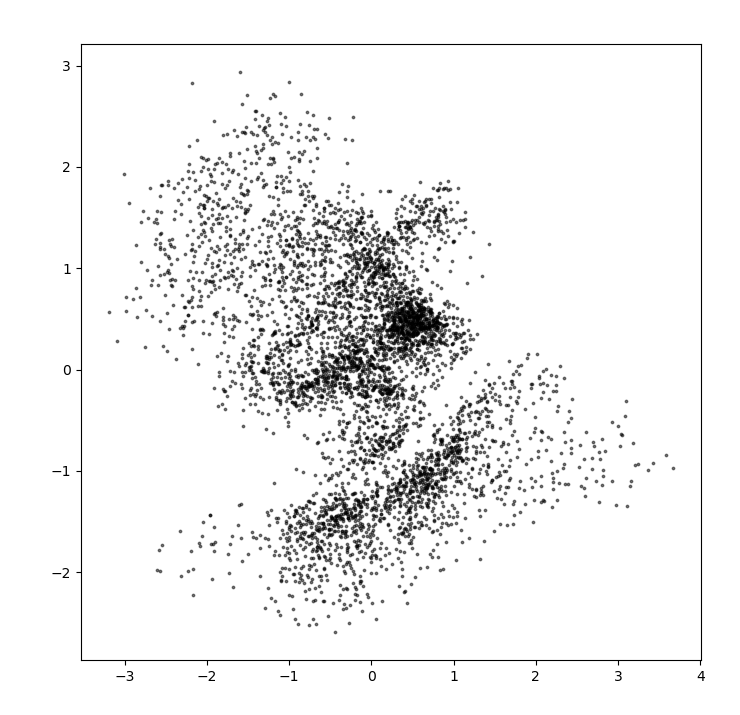
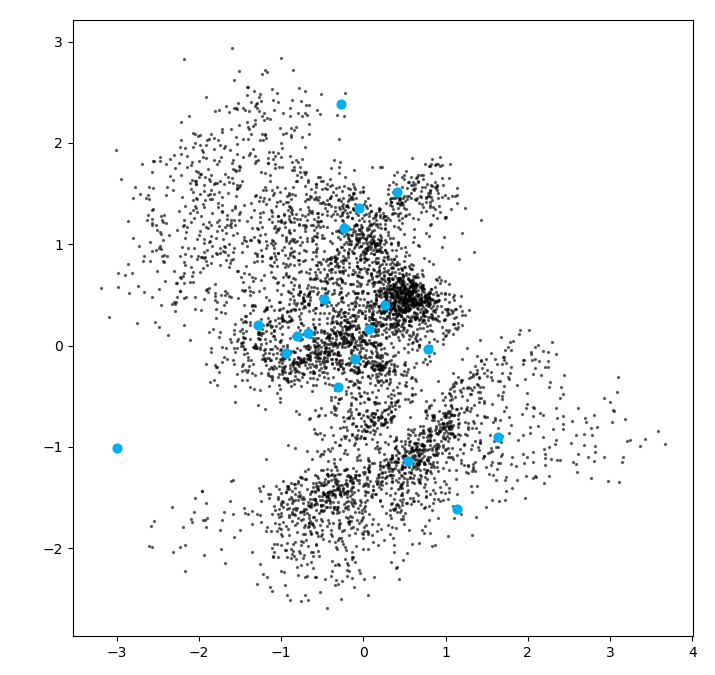
自动编码器存在若干问题，这些问题可以从图中看出。

• 首先，采样空间存在疏密，如橙色点，在密度较高的地方预测会更加准确，而在空白部分则预测不准确。
• 其次，不同种类之间的潜在空间存在交叉，这使得在这些重合部分，生成并不准确。
• 最后，我们很难取的在合理的位置进行采样。

基于这些问题，我们可以使用自动变分编码器改进。

使用pytorch的尝试

目前因为对两种方法的理解否尚且十分有限，也难以比较使用pytorch更方便还是tensorflow更方便，因此在这里补充使用pytorch的方法。

数据预处理

使用tensorflow实现的代码

def preprocess(imgs):
    imgs = imgs.astype("float32") / 255.0
    imgs = np.pad(imgs, ((0, 0), (2, 2), (2, 2)), constant_values=0.0)
    imgs = np.expand_dims(imgs, -1)
    return imgs

• imgs = imgs.astype("float32") / 255.0：这行代码将图像的数据类型转换为浮点数，并将像素值归一化到0-1的范围。这是因为图像的原始像素值通常在0-255之间，归一化可以使得数据更适合神经网络的处理。
• imgs = np.pad(imgs, ((0, 0), (2, 2), (2, 2)), constant_values=0.0)：这行代码对图像进行了填充操作。np.pad函数会在图像的边缘添加额外的像素。这里，它在图像的上下左右各添加了2个像素，填充的值为0。
• imgs = np.expand_dims(imgs, -1)：这行代码增加了一个维度。在处理图像时，我们通常需要一个表示颜色通道的维度。对于彩色图像，这个维度的大小通常为3（对应RGB三个颜色通道）。对于灰度图像，这个维度的大小为1。这行代码就是在最后一个维度（1表示最后一个维度）上增加了一个大小为1的维度。

使用pytorch实现的代码

transform = transform.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5,), (0.5,)),
    transforms.Pad(2)
])

• transforms.ToTensor()：这个转换将PIL图像或者NumPy的ndarray转换为PyTorch的张量（Tensor）。它会将图像的像素强度值从0-255（常见的数据类型为uint8）变为0-1的浮点数，并且，它还会改变数据的维度，它会自动为图像增加一个维度，对于图像，维度通常从(高, 宽, 通道)变为(通道, 高, 宽)。
• transforms.Normalize((0.5,), (0.5,))：这个转换会对张量进行归一化。这里，(0.5,)是均值，(0.5,)是标准差。这意味着，我们会从每个通道中减去0.5，然后除以0.5。这样做可以使得数据的分布接近标准正态分布，即均值为0，标准差为1，有助于神经网络的训练。
• transforms.Pad(2)：这个转换会在图像的每一边添加2个像素的填充。这对于某些卷积神经网络是必要的，因为它们可能会减小图像的尺寸。

数据加载

******************************************************使用tensorflow实现的代码******************************************************

(x_train,y_train), (x_test,y_test) = datasets.fashion_mnist.load_data()
x_train = preprocess(x_train)
x_test = preprocess(x_test)

******************************************使用pytorch实现的代码******************************************

trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)

trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)

自动编码器

原本的编码器的代码不在这里展示。

使用pytorch的实现：

class Autoencoder(nn.Module):
    def __init__(self):
        super(Autoencoder,self).__init__()
        self.encoder = nn.Sequential(
            nn.Conv2d(1,32,3,stride = 2,padding = 1),
            nn.ReLU(),
            nn.Conv2d(32,64,3,stride = 2,padding = 1),
            nn.ReLU(),
            nn.Conv2d(64,128,3,stride = 2,padding = 1),
            nn.ReLU(),
            nn.Flatten(),
            nn.Linear(128*4*4,2)
        )
        self.decoder = nn.Sequential(
            nn.Linear(2,128*4*4),
            nn.Unflatten(1,(128,4,4)),
            nn.ConvTranspose2d(128,64,3,stride = 2,padding = 1,output_padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(64, 32, 3, stride=2, padding=1, output_padding=1),
            nn.ReLU(),
            nn.ConvTranspose2d(32, 1, 3, stride=2, padding=1, output_padding=1),
            nn.Sigmoid()            
        )
    def forward(self,x):
        x = self.encoder(x)
        x = self.decoder(x)
        return x

结构基本与使用keras的实现相同，区别在于不同的函数的参数并不相同。

开始训练

使用相同的优化器和损失函数

model = Autoencoder().cuda()
optimizer = optim.Adam(model.parameters())
loss_function = nn.BCELoss().cuda()

需要自己设置训练循环

for epoch in range(20):
    for data, _ in trainloader:
        data = data.cuda()
        optimizer.zero_grad()
        output = model(data)
        loss = loss_function(output, data)
        loss.backward()
        optimizer.step()
    print(f'Epoch: {epoch+1}, Loss: {loss.item()}')

自动变分编码器

故事

现在假设，您决定分配一个更容易找到该物品的一般区域，而不是将每件衣服放在衣柜中的一个位置。您认为这种更轻松的物品定位方法将有助于解决当前衣柜中局部不连续性的问题。

你将尝试将每件物品区域的中心尽可能靠近衣柜的中间，并且这种偏差距离中心的物品应尽可能接近一米（不小于也不大于）。你越偏离这条规则，你就越需要向布莱恩作为你的造型师支付更多费用。

模型架构的修改

从自动编码器到变分自动编码器，只需要改变编码器和损失函数

向多元正态分布的映射

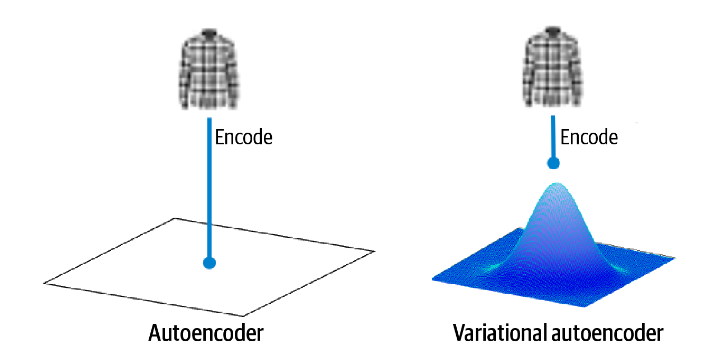
在自动编码器中，每个图像都直接映射到潜在空间中的一个点。在变分自动编码器中，每个图像都被映射到潜在空间中某个点周围的多元正态分布。

正态分布 我们使用如下方式定义正态分布\(N(\mu,\sigma)\)：

\[ f\left(x \mid \mu, \sigma^2\right)=\frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} \]

从输入映射到均值向量和方差向量 编码器将获取每个输入图像并将其编码为均值、方差两个向量，这两个向量共同定义潜在空间中的多元正态分布。

• \(z_{mean}\)
• \(z_{log,var}\)：\(z_{log,var} = log(\sigma^2)\)

由此多元正态分布被定义为：

• \(z = z_{mean}+exp(\frac 12\cdot z_{log,var})\cdot \varepsilon\)

通过这种方式，我们能保证某个点附近的部分也能跟这个点有更多的相似性

采样层

采样层Sampling 随我们要定义一种采样层，允许我们从 \(z_{mean}\) 和 \(z_{log,var}\) 定义的分布中进行采样。

class Sampling(layers.Layer):
	def call(self, inputs):
		z_mean, z_log_var = inputs
		batch = tf.shape(z_mean)[0]
		dim = tf.shape(z_mean)[1]
		epsilon = K.random_normal(shape=(batch, dim))
		return z_mean + tf.exp(0.5 * z_log_var) * epsilon

这段代码定义了一个名为Sampling的类，它继承了layers.Layer这个类，所以它是一个自定义的Keras层。这个自定义层的主要作用是从输入的均值z_mean和对数方差z_log_var定义的多元正态分布中进行采样。

对 Layer 类进行子类化 可以通过对抽象 Layer 类进行子类化并定义调用方法来在 Keras 中创建新层，该方法描述了层如何转换张量。

最重要的方法是 call 方法，它定义了张量在该层中的转换过程。

例如，以下是一个简单的全连接层（即线性层）的实现：

class Linear(layers.Layer):
    def __init__(self, units=32):
        super(Linear, self).__init__()
        self.units = units

    def build(self, input_shape):
        self.w = self.add_weight(shape=(input_shape[-1], self.units),
                                 initializer='random_normal',
                                 trainable=True)
        self.b = self.add_weight(shape=(self.units,),
                                 initializer='zeros',
                                 trainable=True)

    def call(self, inputs):
        return tf.matmul(inputs, self.w) + self.b

在上面的 Linear 层的定义中，build 方法定义了层的权重（w 和 b），call 方法定义了如何使用这些权重来计算该层的输出。

重新参数化技巧 我们可以从标准正态分布中对 epsilon 进行采样，然后手动调整样本以获得正确的均值和方差，而不是直接从参数 z_mean 和 z_log_var 的正态分布中进行采样。它意味着梯度可以在层中自由反向传播。通过保持变量 epsilon 中包含的层的所有随机性，层输出相对于其输入的偏导数可以被证明是确定性的。

********************使用pyTorch实现******************** 在pyTorch中可以用nn.Module 实现类似的功能，在Module中，使用forward来代替layer中的call

class Sampling(nn.Module):
    def forward(self, inputs):
        z_mean, z_log_var = inputs
        batch = z_mean.shape[0]
        dim = z_mean.shape[1]
        epsilon = torch.randn(batch, dim)
        return z_mean + torch.exp(0.5 * z_log_var) * epsilon

修改编码器

tensorflow的修改方案 原本的编码器需要生成一个点，即一个二维的向量。而现在的要分别生成两个二维的向量：均值和方差。因此，将原本的：encoder_output = layers.Dense(2, name="encoder_output")(x) 替换为现在的两行代码：

z_mean = layers.Dense(2, name="z_mean")(x)
z_log_var = layers.Dense(2, name="z_log_var")(x)

并使用新定义的Sampling层，得到最终的分布z

z = Sampling()([z_mean, z_log_var])

pyTorch的修改方案 在pytorch中额外定义上述三层：

self.ZMEAN = nn.Linear(128*4*4,EMBEDDING_DIM)
self.ZLOGVAR = nn.Linear(128*4*4,EMBEDDING_DIM)
self.Sampling = Sampling()

并在forward中依次通过：

def forward(self,x):
    x = self.encoder(x)
    z_mean = self.ZMEAN(x)
    z_log_var = self.ZLOGVAR(x)
    x = self.Sampling([z_mean,z_log_var])
    x = self.decoder(x)
    return z_mean,z_log_var,x

修改损失函数

除了原本的损失函数，需要在其上增加一项Kullback–Leibler (KL) divergence term KL散度项

************************************************KL散度项的定义************************************************ KL 散度是一种衡量一个概率分布与另一个概率分布差异程度的方法。在 VAE 中，我们想要测量参数 z_mean 和 z_log_var 的正态分布与标准正态分布的差异程度。因此，可以由以下公式计算：

\[ D_{K L}\left[N(\mu, \sigma \| N(0,1)\right]=-\frac{1}{2} \sum\left(1+\log \left(\sigma^2\right)-\mu^2-\sigma^2\right) \]

• 在tensorflow中的使用以下公式计算：

kl_loss = tf.reduce_mean(
                tf.reduce_sum(
                    -0.5
                    * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var)),
                    axis=1,
                )
            )

• 在pyTorch中使用以下方法计算：

kl_loss = torch.mean(-0.5 * torch.sum(1 + z_log_var - z_mean.pow(2) - z_log_var.exp(),axis=1))

VAE中，我们希望潜在空间有良好的结构，即相似的数据点应该被映射到潜在空间中的相近位置。通过最小化KL散度损失，我们可以使编码器产生的潜在分布接近于目标分布，这样就可以更好地实现我们的目标，即在潜在空间中有良好的数据组织结构。

新的损失函数和引入模型训练的方式 接下来要将损失函数引入训练过程中。

• tensorflow中的引入方式：重写train_step。这种方法可以保留fit()的遍历想，同时使用自己的方法训练。

def train_step(self, data):
    """Step run during training."""
		# 创建一个tf.GradientTape上下文，只有这个上下文中所有的操作会被记录，用于之后的计算梯度
    with tf.GradientTape() as tape:
        z_mean, z_log_var, reconstruction = self(data)
        # 计算重构损失，这是原始输入数据和重构数据之间的二元交叉熵损失的平均值。
				reconstruction_loss = tf.reduce_mean(
            BETA
            * losses.binary_crossentropy(
                data, reconstruction, axis=(1, 2, 3)
            )
        )
				# 计算KL散度损失，这是从标准正态分布到模型的潜在分布的KL散度。
        kl_loss = tf.reduce_mean(
            tf.reduce_sum(
                -0.5
                * (1 + z_log_var - tf.square(z_mean) - tf.exp(z_log_var)),
                axis=1,
            )
        )
				# 得到总的损失
        total_loss = reconstruction_loss + kl_loss
		# 计算总损失关于可训练权重的梯度
    grads = tape.gradient(total_loss, self.trainable_weights)
		# 使用优化器应用这些梯度，以更新权重
    self.optimizer.apply_gradients(zip(grads, self.trainable_weights))
		# 更新损失跟踪器的状态，这些跟踪器用于跟踪训练过程中的损失。
    self.total_loss_tracker.update_state(total_loss)
    self.reconstruction_loss_tracker.update_state(reconstruction_loss)
    self.kl_loss_tracker.update_state(kl_loss)
    return {m.name: m.result() for m in self.metrics}

• 在pyTorch中的引入，只需要在相应的训练过程中使用新定义的损失函数即可。相对来说比较简单。

for epoch in range(EPOCHS):
    for x,_ in trainloader:
        x = x.cuda()
        z_mean,z_log_var,reconstruction = vae(x)
        loss = vae.loss_function(x,z_mean,z_log_var,reconstruction)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    test_loss = 0
    for y,_ in testloader:
        y = y.cuda()
        z_mean,z_log_var,reconstruction = vae(y)
        test_loss += vae.loss_function(y,z_mean,z_log_var,reconstruction)
    test_loss /= len(testloader)
    print(f"Epoch: {epoch+1},  Test Loss: {test_loss}")

训练结果

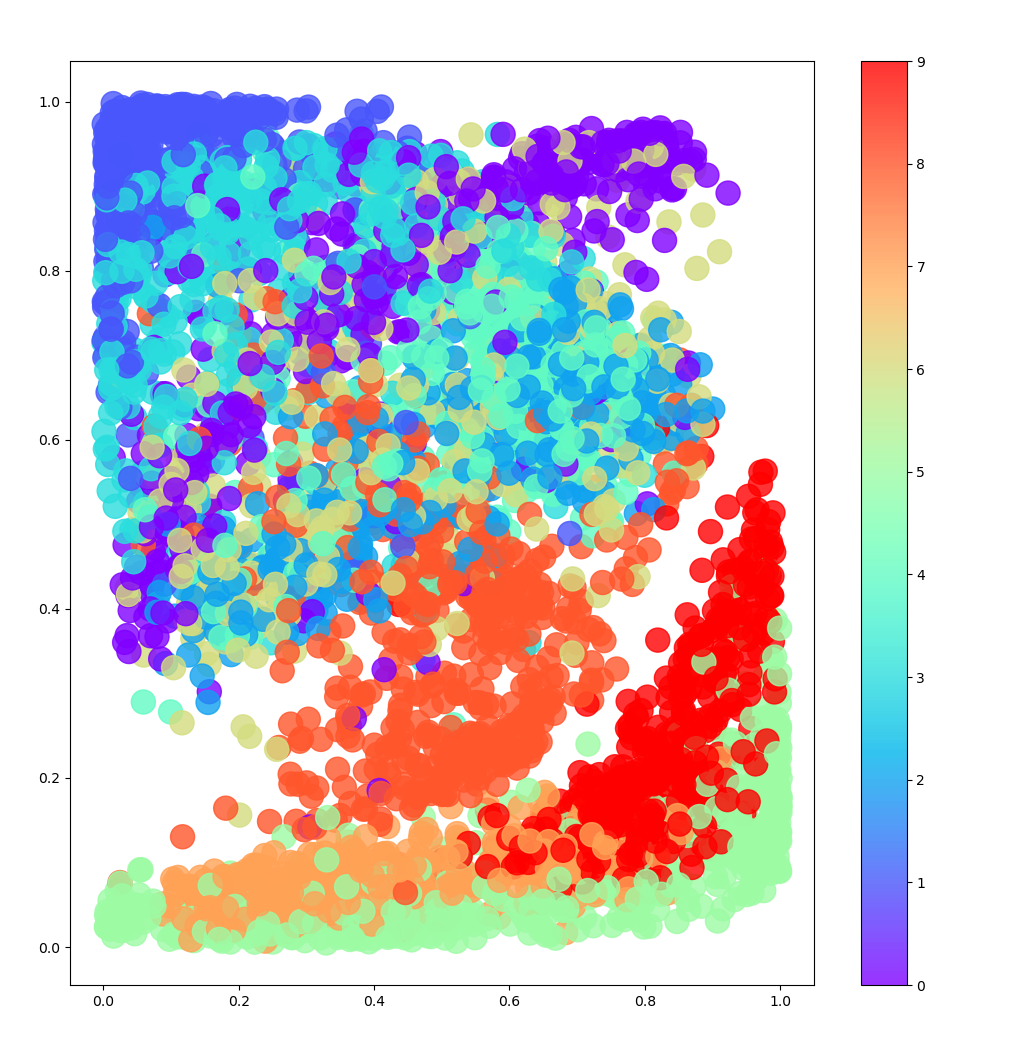
KL 散度损失项确保编码图像的 z_mean 和 z_log_var 值永远不会偏离标准正态分布太远。由于编码器现在是随机的，而不是确定性的，因此潜在空间现在更加连续，因此不存在太多形成不良的图像。

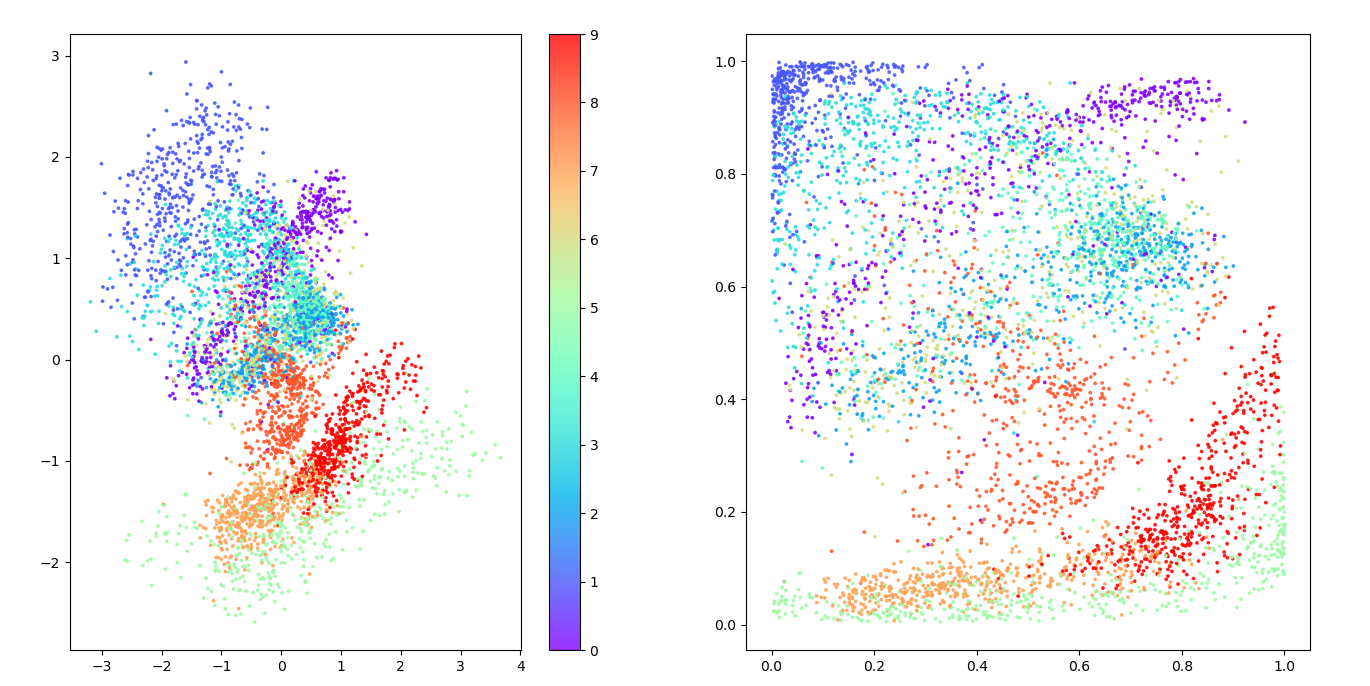
通过按服装类型对潜在空间中的点进行着色，我们可以看到没有任何一种类型受到优先对待。右侧图显示了转换为 p 值的空间 - 我们可以看到每种颜色的表示大致相同。再次强调，重要的是要记住，在训练期间根本没有使用标签； VAE 自行学习了各种形式的服装，以帮助最大限度地减少重建损失。

更高维度的VAE

CelebA数据集

我们将使用 CelebFaces Attributes (CelebA) 数据集来训练我们的下一个变分自动编码器。这是超过 200,000 张名人面孔彩色图像的集合，每张图像都附有各种标签（例如戴帽子、微笑等）。

数据集加载

tensorflow的加载方式 使用tensorflow的函数image_dataset_from_directory 从指定的地址加载图像数据。

train_data = utils.image_dataset_from_directory(
    "/app/data/celeba-dataset/img_align_celeba/img_align_celeba",
    labels=None,
    color_mode="rgb",
    image_size=(IMAGE_SIZE, IMAGE_SIZE),
    batch_size=BATCH_SIZE,
    shuffle=True,
    seed=42,
    interpolation="bilinear",
)
# Preprocess the data
def preprocess(img):
    img = tf.cast(img, "float32") / 255.0
    return img
train = train_data.map(lambda x: preprocess(x))

• labels=None：表示不从目录结构中推断标签，因为这可能是一个无监督学习任务。
• color_mode="rgb"：表示将图像加载为 RGB 三通道。
• image_size=(IMAGE_SIZE, IMAGE_SIZE)：表示将图像调整为指定的大小。
• batch_size=BATCH_SIZE：表示在每次迭代中从数据集中抽取的样本数量。
• shuffle=True：表示在每个 epoch 开始时都要打乱数据集。
• seed=42：这是随机数生成器的种子，用于打乱数据集和进行其他随机操作。
• interpolation="bilinear"：这是用于调整图像大小时的插值方法。
• 最后使用preprocess函数处理这些图像，train = train_data.map(lambda x: preprocess(x)) 意味着将这个函数作用在训练集的所有数据上。

pyTorch的加载方式 可以使用ImageFolder 从指定地址加载数据集，并定义自己transform函数来实现转换。相对来说要比keras简单一些。

# 定义转换
transform = transforms.Compose([
    transforms.Resize((IMAGE_SIZE, IMAGE_SIZE)),  # 调整图像大小
    transforms.ToTensor(),  # 将 PIL 图像或 NumPy ndarray 转换为 tensor
    transforms.Normalize(mean=[0.5, 0.5, 0.5], std=[0.5, 0.5, 0.5])  # 标准化
])

# 加载数据集
dataset = datasets.ImageFolder("/app/data/celeba-dataset/img_align_celeba/img_align_celeba", transform=transform)

# 创建数据加载器
dataloader = DataLoader(dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=4)

模型修改

模型的修改涉及到网络上的修改和参数的优化，可直接参考原书的代码，由于基本结构没有变化，只需要根据需要修改的参数和网络修改相应代码即可，这里不再详述。

潜在空间分析

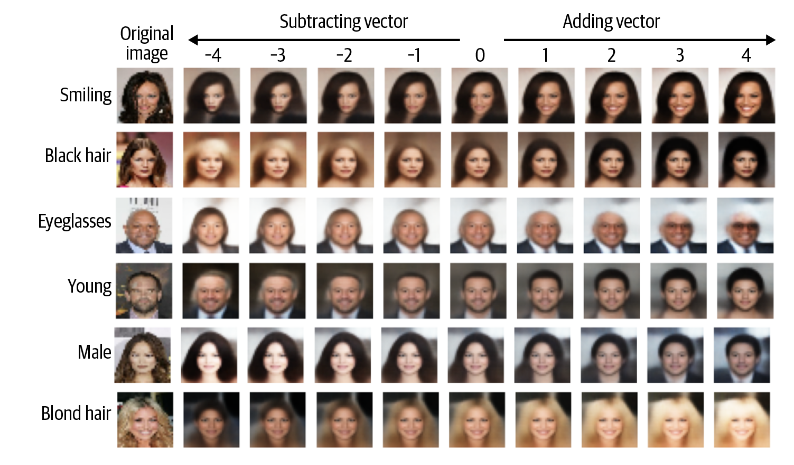
假设我们想拍摄一张看起来悲伤的人的照片并给他们一个微笑。为此，我们首先需要在潜在空间中找到一个指向微笑增加方向的向量。将此向量添加到潜在空间中原始图像的编码中将为我们提供一个新点，在解码时，该新点应该为我们提供原始图像的更多笑脸版本。

Smiling特征向量

CelebA 数据集中的每张图像都标有属性，其中之一是微笑。如果我们将具有 Smiling 属性的编码图像在潜在空间中的平均位置减去不具有 Smiling 属性的编码图像的平均位置，我们将获得指向 Smiling 方向的向量。

\[ z_{new} = z+\alpha\cdot feature\_vecture \]

再将这个特征向量一个\(\alpha\)的比例系数加载原本的向量上，则可以得到一个更加接近与微笑的向量。

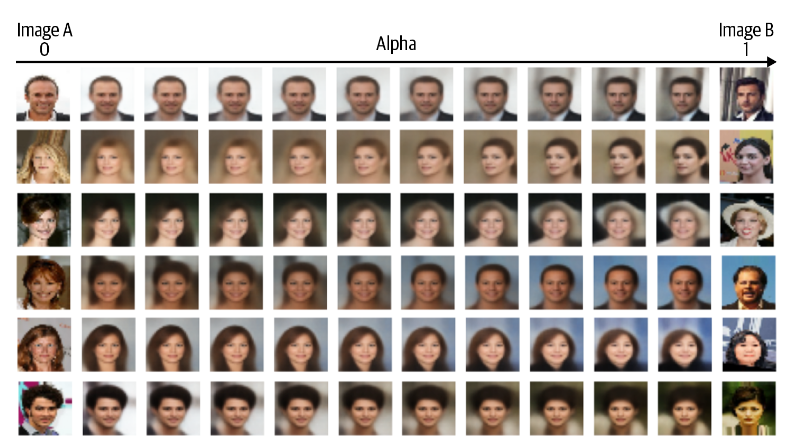
面部信息混合

想象潜在空间中的两个点 A 和 B，它们代表两个图像。如果您从 A 点开始，沿直线朝 B 点走，边走边解码线上的每个点，您会看到从起始面到结束面的逐渐过渡。由此可以实现面部信息的混合。

\[ z_{new} = z_A * (1- \alpha) + z_B * \alpha \]

总结

在本章中，我们了解到变分自动编码器是生成模型工具箱中的一种强大工具。我们首先探索了如何使用普通的自动编码器将高维度的图像映射到低维度的潜在空间，从而从各个无信息的像素中提取出高级特征。然而，我们很快发现使用普通自动编码器作为生成模型存在一些缺点，例如，从学习的潜在空间中进行采样存在问题。

变分自动编码器通过引入随机性和约束潜在空间中的点分布来解决这些问题。我们看到，通过一些小的调整，我们可以将我们的自动编码器转变为变分自动编码器，从而赋予它成为真正的生成模型的能力。

最后，我们将新的技术应用到面部生成问题中，看到我们如何可以简单地从标准正态分布中解码点来生成新的面部。此外，通过在潜在空间内进行向量算术，我们可以实现一些惊人的效果，如面部变形和特征操作。