Chapter 2 Deep Learning

神经网络

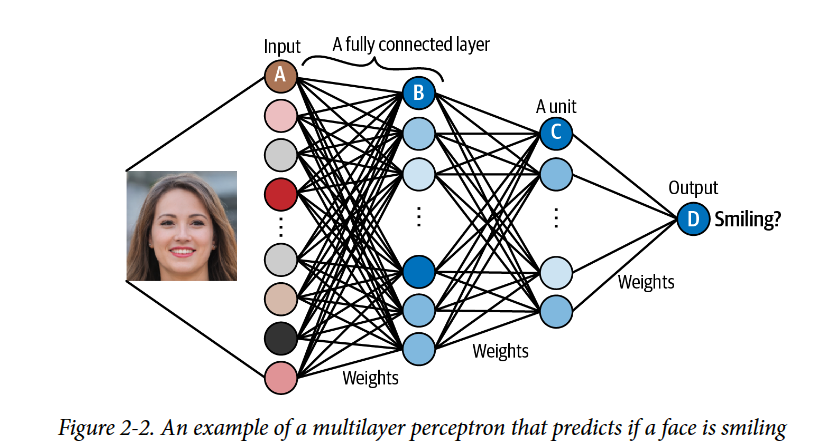
神经网络由一系列堆叠层组成。每层都包含通过一组权重连接到前一层单元的单元。正如我们将看到的，有许多不同类型的层，但最常见的一种是全连接（或密集）层，它将层中的所有单元直接连接到前一层中的每个单元。

MLP

所有相邻层完全连接fully connected的神经网络称为多层感知器（MLP）

学习高级特征

神经网络如此强大的关键特性是它们能够在没有人类指导的情况下从输入数据中学习特征。

单元A接收输入像素的单个通道的值。

单元B组合其输入值，以便在存在特定的低级特征（如边缘）时最强烈地触发。

单元C组合低级特征，以便在图像中看到更高级的特征（如牙齿）时最强烈地触发。

单元D组合高级特征，以便在原始图像中的人在微笑时最强烈地触发。

MLP的实践

TensorFlow & Keras

TensorFlow 是一个用于机器学习的开源 Python 库，由 Google 开发。Keras 是一个用于构建神经网络的高级 API，构建在 TensorFlow 之上。

数据集和one-hot的编码向量

使用CIFAR-10数据集作为训练数据，训练图像数据（x_train）存储在形状为[50000,32,32,3]的张量中。并将标签改为one-hot编码。如果图像的类整数标签是 i，那么它的 one-hot 编码是一个长度为 10（类数）的向量，除了第 i 个元素（即 1）之外的所有元素都为 0。这些步骤显示为 i。

import numpy as np
from tensorflow import keras
from keras import datasets,utils
# 因为未知的原因，原代码from tensorflow.keras import datasets, utils并不能正常工作，反而如上写可以

(x_train, y_train), (x_test, y_test) = datasets.cifar10.load_data()
NUM_CLASSES = 10

x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0

y_train = utils.to_categorical(y_train, NUM_CLASSES)
y_test = utils.to_categorical(y_test, NUM_CLASSES)

.astype('float32') / 255.0 归一化
utils.to_categorical(y_train, NUM_CLASSES) 将标签改为one-hot编码

建立模型

使用sequential风格的建模方式

from tensorflow import keras
from keras import layers, models

model = models.Sequential([
    layers.Flatten(input_shape=(32, 32, 3)),
    layers.Dense(200, activation='relu'),
    layers.Dense(150, activation='relu'),
    layers.Dense(10, activation='softmax')
])

使用functional API的建模方式

input_layer= layers.Input(shape=(32, 32, 3))
x = layers.Flatten()(input_layer)
x = layers.Dense(200, activation='relu')(x)
x = layers.Dense(150, activation='relu')(x)
output_layer = layers.Dense(10, activation='softmax')(x)
model = models.Model(inputs=input_layer, outputs=output_layer)

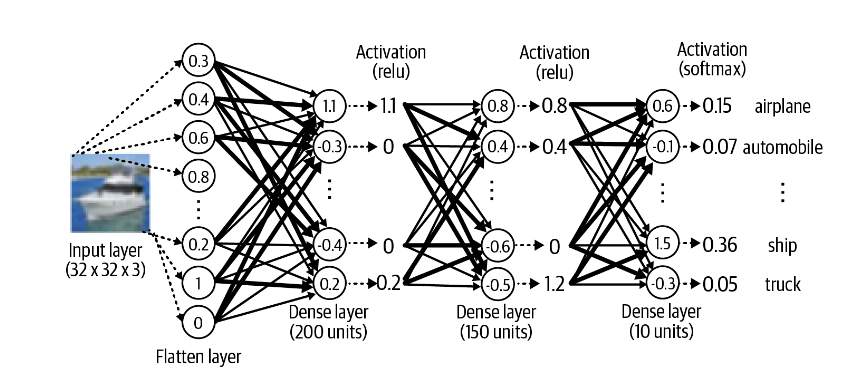
为了构建我们的 MLP，我们使用了三种不同类型的层：Input、Flatten 和 Dense。

输入层是网络的入口点。我们告诉网络每个数据元素的形状，期望为元组。请注意，我们没有指定批大小，这不是必需的，因为我们可以同时将任意数量的图像传递到输入层。我们不需要在输入层定义中明确说明批处理大小。
我们使用 Flatten 层将此输入展平为矢量。这会产生长度为 3,072 （2 32 x 32 x 3）的矢量。我们这样做的原因是，后续的 Dense 层要求其输入是平面的，而不是多维数组。
密集层是神经网络最基本的构建块之一。它包含与前一层密集连接的给定数量的单元，也就是说，该层中的每个单元都通过带有权重（可以是正值或负值）的单个连接与前一层中的每个单元连接。给定单元的输出是它从前一层接收的输入的加权和。
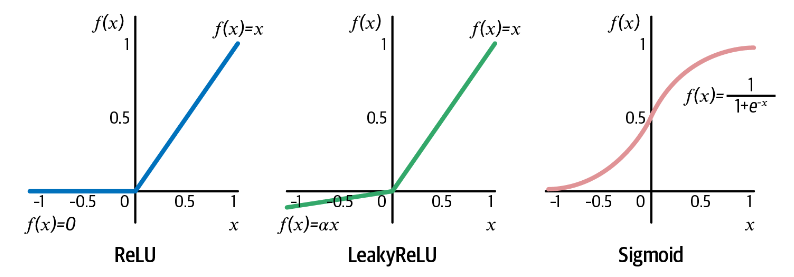
然后通过非线性激活函数，然后发送到下一层。激活函数对于确保神经网络能够学习复杂的函数并且不仅仅输出其输入的线性组合至关重要。

激活函数

两种使用激活函数的方法

# 以activation参数使用激活函数
x = layers.Dense(units=200, activation = 'relu')(x)
# 以激活函数层使用激活函数
x = layers.Dense(units=200)(x)
x = layers.Activation('relu')(x)

检查模型

使用model.summary()检查模型

_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 input_1 (InputLayer)        [(None, 32, 32, 3)]       0

 flatten_1 (Flatten)         (None, 3072)              0

 dense_3 (Dense)             (None, 200)               614600

 dense_4 (Dense)             (None, 150)               30150

 dense_5 (Dense)             (None, 10)                1510

=================================================================
Total params: 646,260
Trainable params: 646,260
Non-trainable params: 0
_________________________________________________________________

Keras 使用 None 作为第一个维度的标记，以表明它尚不知道将传递到网络中的观测值数量。事实上，它不需要；我们可以轻松地通过网络一次传递 1 个观察结果，就像一次传递 1,000 个观察结果一样。这是因为张量运算是使用线性代数同时在所有观测值上进行的
如果发现模型训练速度太慢，请检查摘要以查看是否有任何层包含大量权重。如果是这样，应该考虑是否可以减少层中的单元数量以加快训练速度

编译模型：优化器和损失函数

1
2
3

opt = optimizers.Adam(learning_rate=0.0005)
model.compile(loss='categorical_crossentropy', optimizer=opt,
metrics=['accuracy'])

优化器

Keras documentation: Optimizers

****************损失函数****************

Keras documentation: Losses

训练模型

model.fit(x_train
        , y_train
        , batch_size = 32
        , epochs = 10
        , shuffle = True
        )

batch_size 确定了在每个训练步骤中将传递给网络的观察值数量。
epochs 确定网络将显示完整训练数据的次数。
如果 shuffle = True，那么在每个训练步骤中，批次将从训练数据中随机不重复地抽取。

评价模型

1 2	>> model.evaluate(x_test, y_test) 313/313 [==============================] - 1s 3ms/step - loss: 1.4345 - accuracy: 0.4900

CLASSES = np.array(['airplane', 'automobile', 'bird', 'cat', 'deer', 'dog'
, 'frog', 'horse', 'ship', 'truck'])
preds = model.predict(x_test)
preds_single = CLASSES[np.argmax(preds, axis = -1)]
actual_single = CLASSES[np.argmax(y_test, axis = -1)]
n_to_show = 10
indices = np.random.choice(range(len(x_test)), n_to_show)
fig = plt.figure(figsize=(15, 3))
fig.subplots_adjust(hspace=0.4, wspace=0.4)
for i, idx in enumerate(indices):
    img = x_test[idx]
    ax = fig.add_subplot(1, n_to_show, i+1)
    ax.axis('off')
    ax.text(0.5, -0.35, 'pred = ' + str(preds_single[idx]), fontsize=10
    , ha='center', transform=ax.transAxes)
    ax.text(0.5, -0.7, 'act = ' + str(actual_single[idx]), fontsize=10
    , ha='center', transform=ax.transAxes)
    ax.imshow(img)

卷积神经网络

卷积核和卷积层

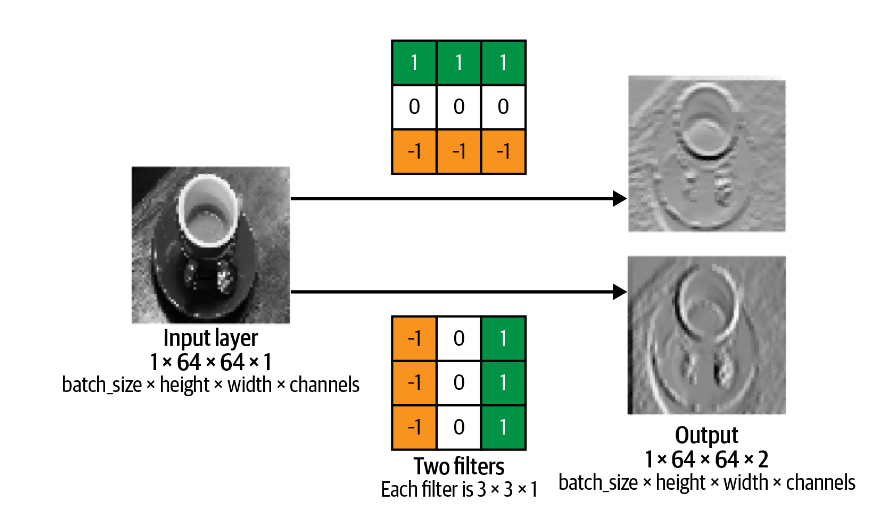
卷积核 左图显示了灰度图像的两个不同的 \(3 × 3 × 1\) 部分与 \(3 × 3 × 1\) 卷积核进行卷积。卷积是通过将卷积核按像素与图像的部分相乘并对结果求和来执行的。当图像的部分与滤波器紧密匹配时，输出更正，而当图像的部分与滤波器相反时，输出更负。

卷积层 卷积层是卷积核的集合。更多的卷积核会带来更大的深度

input_layer = layers.Input(shape=(64,64,1))
conv_layer_1 = layers.Conv2D(
filters = 2
, kernel_size = (3,3)
, strides = 1
, padding = "same"
)(input_layer)

strides 参数是层在输入上移动过滤器时使用的步长。因此，增加步幅会减小输出张量的大小。例如，当步幅= 2时，输出张量的高度和宽度将是输入张量大小的一半。
padding = "same" 输入参数用零填充输入数据，以便当步长 = 1 时，该层的输出大小与输入大小完全相同。padding =’valid’时，输出不会用0填充。

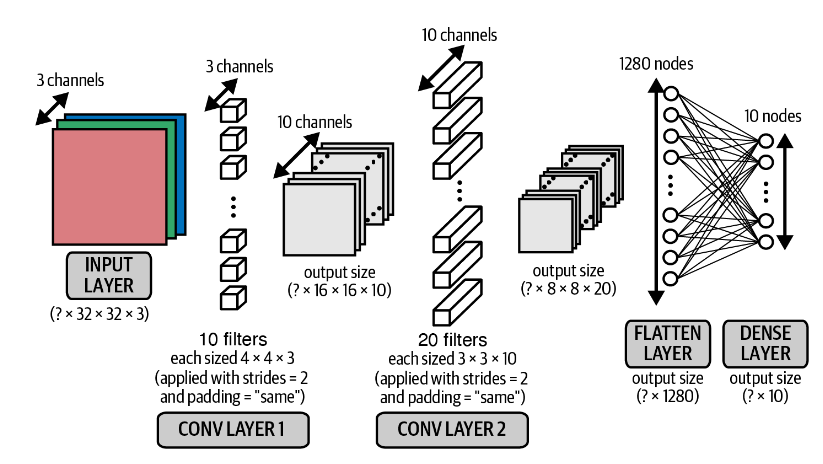
卷积模型

input_layer = layers.Input(shape=(32,32,3))
conv_layer_1 = layers.Conv2D(
filters = 10
, kernel_size = (4,4)
, strides = 2
, padding = 'same'
)(input_layer)
conv_layer_2 = layers.Conv2D(
filters = 20
, kernel_size = (3,3)
, strides = 2
, padding = 'same'
)(conv_layer_1)
flatten_layer = layers.Flatten()(conv_layer_2)
output_layer = layers.Dense(units=10, activation = 'softmax')(flatten_layer)
model = models.Model(input_layer, output_layer)

注意这里stride = 2来代替了池化层的作用
未使用激活函数
第一个卷积层中的每个滤波器的深度为 3 而不是 1，第二个卷积层中每个滤波器深度为20

_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 input_1 (InputLayer)        [(None, 32, 32, 3)]       0
                                     

 conv2d (Conv2D)             (None, 16, 16, 10)        490
                                     

 conv2d_1 (Conv2D)           (None, 8, 8, 20)          1820
                                     

 flatten (Flatten)           (None, 1280)              0
0)                12810

=================================================================
Total params: 15,120
Trainable params: 15,120
Non-trainable params: 0
_________________________________________________________________

协变量偏移&批量归一化

训练深度神经网络时的一个常见问题是确保网络的权重保持在合理的值范围内 - 如果它们开始变得太大，则表明您的网络正在遭受所谓的“梯度爆炸问题。随着误差通过网络向后传播，早期层中的梯度计算有时会呈指数级增长，导致权重值剧烈波动。如果您的损失函数开始返回 NaN，则您的权重很可能已经变得足够大，足以导致溢出错误。当您开始训练网络时，这不一定会立即发生。

协变量偏移 最初我们将所有的像素值缩放到-1到1，随着网络训练和权重远离其随机初始值，这种缩放可能开始失效。这种现象称为协变量偏移。

********************批量归一化******************** 在训练期间，批量归一化层计算整个批次中每个输入通道的平均值和标准差，并通过减去平均值并除以标准差来进行归一化。

我们可以在密集层或卷积层之后放置批量归一化层来归一化输出
**layers.BatchNormalization(momentum = 0.9)**

Dropout

如果一个算法在训练数据集上表现良好，但在测试数据集上表现不佳，我们就说它出现了过度拟合 overfitting。为了解决这个问题，我们使用正则化技术，确保模型在开始过度拟合时受到惩罚。

规范机器学习算法的方法有很多，但对于深度学习，最常见的方法之一是使用 dropout 层。

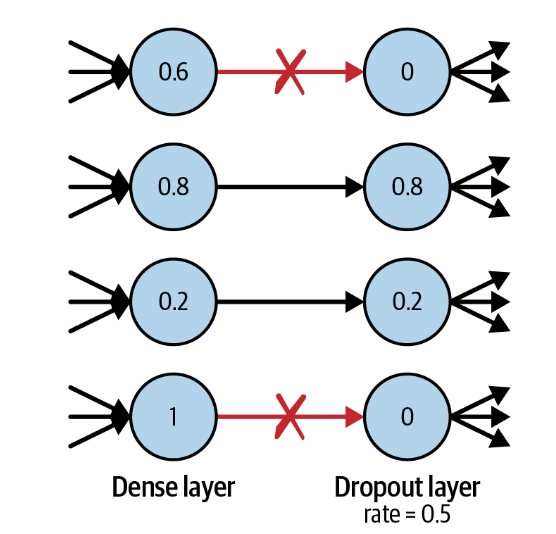
Dropout 层非常简单。在训练过程中，每个 dropout 层从前一层中随机选择一组单元，并将其输出设置为 0
如果我们使用 dropout 层，网络就不会过多依赖任何一个单元，因此知识会更均匀地分布在整个网络中。

在 dropout 层中不需要学习权重，因为要丢弃的单位是随机决定的。在预测时，丢弃层不会丢弃任何单元，因此整个网络用于进行预测。
**layers.Dropout(rate = 0.25)**
Dropout 层最常在密集层之后使用，因为这些层由于权重数量较多而最容易出现过度拟合，尽管您也可以在卷积层之后使用它们

建立CNN模型

input_layer = layers.Input((32,32,3))
x = layers.Conv2D(filters = 32, kernel_size = 3
, strides = 1, padding = 'same')(input_layer)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)

x = layers.Conv2D(filters = 32, kernel_size = 3, strides = 2, padding = 'same')(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)

x = layers.Conv2D(filters = 64, kernel_size = 3, strides = 1, padding = 'same')(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)

x = layers.Conv2D(filters = 64, kernel_size = 3, strides = 2, padding = 'same')(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)

x = layers.Flatten()(x)

x = layers.Dense(128)(x)
x = layers.BatchNormalization()(x)
x = layers.LeakyReLU()(x)
x = layers.Dropout(rate = 0.5)(x)

output_layer = layers.Dense(10, activation = 'softmax')(x)
model = models.Model(input_layer, output_layer)

_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 input_1 (InputLayer)        [(None, 32, 32, 3)]       0

 conv2d (Conv2D)             (None, 32, 32, 32)        896

 batch_normalization (BatchN  (None, 32, 32, 32)       128
 ormalization)

 leaky_re_lu (LeakyReLU)     (None, 32, 32, 32)        0

 conv2d_1 (Conv2D)           (None, 16, 16, 32)        9248

 batch_normalization_1 (Batc  (None, 16, 16, 32)       128
 hNormalization)

 leaky_re_lu_1 (LeakyReLU)   (None, 16, 16, 32)        0

 conv2d_2 (Conv2D)           (None, 16, 16, 64)        18496

 batch_normalization_2 (Batc  (None, 16, 16, 64)       256
 hNormalization)

 leaky_re_lu_2 (LeakyReLU)   (None, 16, 16, 64)        0

 conv2d_3 (Conv2D)           (None, 8, 8, 64)          36928

 batch_normalization_3 (Batc  (None, 8, 8, 64)         256
 hNormalization)

 leaky_re_lu_3 (LeakyReLU)   (None, 8, 8, 64)          0

 flatten (Flatten)           (None, 4096)              0

 dense (Dense)               (None, 128)               524416

 batch_normalization_4 (Batc  (None, 128)              512
 hNormalization)

 leaky_re_lu_4 (LeakyReLU)   (None, 128)               0

 dropout (Dropout)           (None, 128)               0

 dense_1 (Dense)             (None, 10)                1290

=================================================================
Total params: 592,554
Trainable params: 591,914
Non-trainable params: 640
_________________________________________________________________

Summary

本章介绍了开始建立深度生成模型所需的核心深度学习概念。我们首先使用Keras构建了一个多层感知器(MLP)，并训练该模型预测CIFAR-10数据集中给定图像的类别。然后，我们通过引入卷积、批处理标准化和dropout层来改进这个架构，创建了一个卷积神经网络(CNN)。

本章的一个非常重要的要点是，深度神经网络在设计上是完全灵活的，当涉及到模型架构时，实际上没有固定的规则。虽然有指导方针和最佳实践，但应该随意实验层和它们出现的顺序。