Chapter 1 Generative Modeling

Generative modeling is a branch of machine learning that involves training a model to produce new data that is similar to a given dataset.

概念

深度学习模型

以生成与提供的数据集相似的新数据为目的的机械学习分支。

• 训练数据包含很多例子，其中每一个数据点被称为一个观察 observation
• 每个观察包含很多特征 feature
• 我们的目标是构建一个模型，该模型可以生成新的特征集，这些特征集看起来就像是使用与原始数据相同的规则创建的。
• 生成式模型应该是概率的probabilistic 而不是确定的deterministic

与判别式模型的区别

• 判别式模型预测\(p(y \mid x)\)
• 生成式模型预测\(p(x)\)，或者在一定情况下预测\(p(x|y)\)
  • For example, if our dataset contains different types of fruit, we could tell our generative model to specifically generate an image of an apple.

生成式模型是解锁一种更复杂的人工智能形式的关键

• 首先，纯粹从理论角度来看，我们不应该将机器训练限制在简单的数据分类上。为了完整性，我们还应该关注训练模型，以获取对数据分布的更完整的理解，而不是任何特定的标签
• 其次，生成建模现在正被用于推动人工智能其他领域的进步
• 最后，如果我们真的要说我们已经建造了一台机器，它获得了与人类相当的智能形式，那么生成建模肯定是解决方案的一部分

我们的第一个生成式模型

感知数据空间

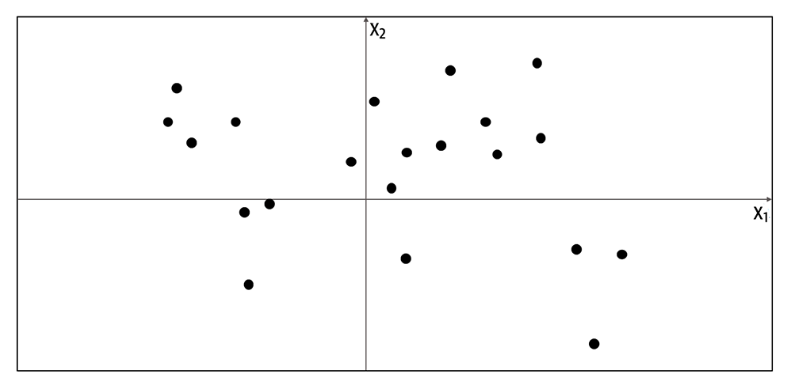
• 观察的集合：点
• 我们假设这些观察生成于一个未知的分布\(p_{data}\)
• 构建一个生成式模型\(p_{model}\)，使得这个模型生成的数据看起来是\(p_{data}\)生成的

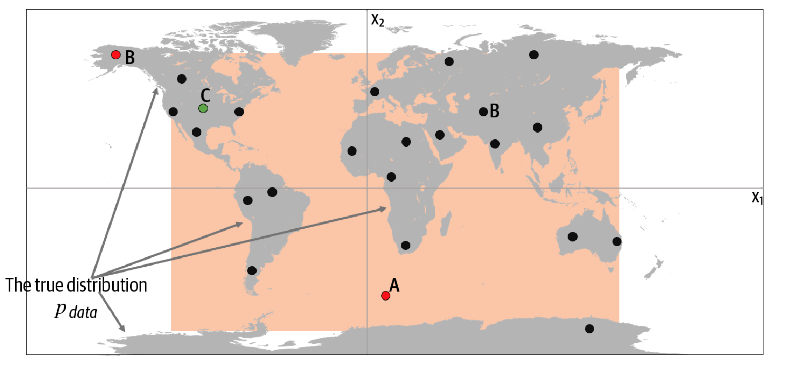
数据空间重合 如上图，我们观察这些点，可能得到第二幅图中橙色的区域。按照这个区域我们随机生成一个红色的点A。但实际的分布是仅仅生成在大陆上，所以我们生成的数据并没有看起来是\(p_{data}\)生成的数据。这是生成模型的空间包含了原数据空间不包括的区域。而红色的点B则在橙色区域之外，不可能由\(p_{model}\)生成，这是生成模型没有包含应该包含的区域。

容易生成 尽管有缺点，但该模型很容易采样，因为它只是橙色盒子上的单一分布。

表征学习 representation learning

我们不试图直接对高维样本空间进行建模，而是使用一些低维潜在空间来描述训练集中的每个观测，然后学习一个映射函数，该函数可以获取潜在空间中的一个点，并将其映射到原始域中的一点。

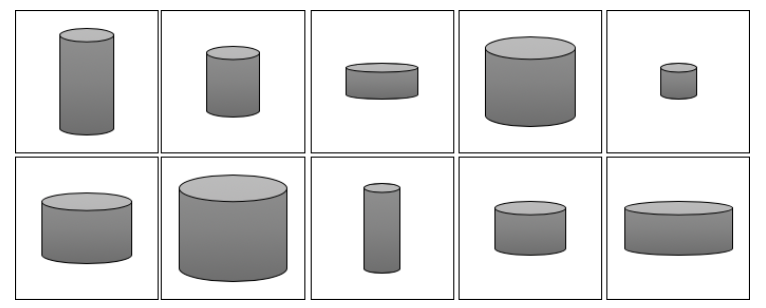
具体来说，如上述10个图形中，尽管他们都是3维的图形，但我们知道，我们只需要知道底面半径和高即可。他因此我们可以通过适当的映射函数，从一个二维的潜在空间用于生成新的圆柱体。

核心概率论

关键术语

• 样本空间：所有可能的观测可取的值。比如之前世界地图的例子，所有经纬度对应的点都是样本空间的点，无论它是否是真是的数据分布中的一个点。
• 概率密度函数：如名；在之前的例子中，所有橙色框中的概率密度函数的积分为1，框外的概率密度函数为0
• 参数化建模：参数化建模是一种通过部分参数来对\(p_{model}\)建模，在这种建模方法下，存在参数集合\(\theta\)，使得\(p_{\theta}(x) = p_{model}(x)\)。在先前的例子中，我们可以使用四个坐标描述橙色框，即\(p_{(x_1,x_2,x_3,x_4)}(x) = p_{model}(x)\)
• 似然Likelihood：似然的定义是在当前参数集\(\theta\)下，观测点x的概率密度。\(\mathscr{L}(\theta \mid \mathbf{x})=p_\theta(\mathbf{x})\)。对于观测点的集合X，其似然定义为：\(\mathscr{L}(\theta \mid \mathbf{X})=\prod_{\mathbf{x} \in \mathbf{X}} p_\theta(\mathbf{x})\)。
  • 在先前的例子中，一个只覆盖地图左半部分的橙色方框的可能性为0——它不可能生成数据集，因为我们在地图右半部分观察到了点，这些点的概率为0。
  • 为了方便计算，我们使用对数似然：\(\ell(\theta \mid \mathbf{X})=\sum_{\mathbf{x} \in \mathbf{X}} \log p_\theta(\mathbf{x})\)
  • 最重要的是，**********************************************************************************************************似然是参数的函数而非观察的函数**********************************************************************************************************
  • 参数化建模的重点即为最大化似然函数
• **************************最大似然估计：**************************如上所属，应最大化似然。最大似然被定义为：\(\hat \theta = argmax_{x}\ell(\theta|X)\)
  • 在上例中，最大似然估计是包含所有点的最小矩阵
  • 最小化负对数似然函数：\(\hat \theta = argmin_{x}(-\ell(\theta|X))\)
  • 当然，实际上在深度学习中，不可能直接计算最小的似然函数

生成式模型分类

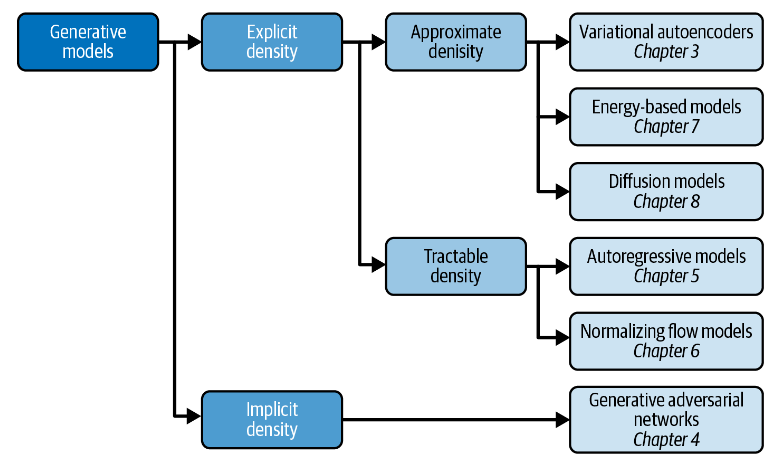
根据模型的建立方式，大致有三个大类：

• 对密度函数进行显式建模，但以某种方式约束模型
  • 可处理模型对模型架构施加了约束，使得密度函数具有易于计算的形式。例如，自回归模型对输入特征进行排序，以便可以按顺序生成输出——例如，逐个单词或逐个像素。归一化流模型将一系列易于处理的可逆函数应用于简单分布，以生成更复杂的分布
• 对密度函数的易于处理的近似进行显式建模
  • 近似密度模型包括变分自动编码器，它引入潜在变量并优化联合密度函数的近似。基于能量的模型也利用近似方法，但通过马尔可夫链采样而不是变分方法来实现。扩散模型通过训练模型逐渐对先前已损坏的给定图像进行去噪来近似密度函数。
• 通过直接生成数据的随机过程对密度函数进行隐式建模
  • 隐式密度模型根本不旨在估计概率密度，而是仅专注于产生直接生成数据的随机过程。隐式生成模型最著名的例子是生成对抗网络。