评价和检验

假设检验 Test d’hypothese

假设一个参数, 检验是否合理

降雨量的例子

我们讨论我们有9年的降雨量数据, 符合\(LG(600,100)\), 我们检验\(*H0: m = 600*\), 取对立假设\(*H1: m = 650*\), 有6%的选错的风险

• 首先, 考虑均值满足正态分布\(LG(600,100/\sqrt{9})\), 求\(P(\overline{X}>K) = 5\%\), 以求出阈值\(k\), 最终再验证均值是否超过阈值

  \[ \begin{aligned} &P(\frac{\overline{x}-600}{100/3}>\frac{k-600}{100/3}) = 0.05 \\&P(\frac{\overline{x}-600}{100/3}<\frac{k-600}{100/3}) = 0.95= 1-\alpha\\ &k = 655\end{aligned} \]

  我们称

  • \(k<655\)为H0的接受域
  • \(k>655\)的范围为H0的拒绝域

• 发现均值\(\overline{X}<k\), 接受H0

• 然后，我们研究H0接收域中的风险，设均值满足\(LG(650,100/\sqrt{9})\)：

  \[ \begin{aligned} 1-\beta &= P(\overline{X} > k)\\ &=P(\frac{\overline{X}-\mathbf{650}}{100/3}>\frac{655-650}{100/3})\\ &= 0.56\end{aligned} \]

• 说明之前假设的不好

解释

在选择中, α被称为弃真错误, 我们认为H0是真的情况下, 被抛弃的概率

而β是假设H0是假的的情况下的,错误的的概率,被称为取伪错误, 参见图片7

弃真错误和取伪错误

• 风险 risque: \(\beta\)
• 检验功效 puissance du test：\(1-\beta\)

	H0	H1
H0	1 − α	β
H1	α	1 − β

一般过程

1. 确定第一类错误 α

2. 确定hypothese H0, H1

3. 确定决策变量，比如均值，方差, 也可以使用似然函数来确定

4. 计算拒绝域région cristique RC：

\(*P(RC|H0) = α*\)

5. 根据样本计算统计值

6. 拒绝或者接收

7. 计算第二类错误puissance du test: \(*P(RC|H1) = 1 − β*\)

检验统计量 Neyman-Pearson

简单的假设检验 hypothèse simple

假设

\[ \begin{aligned} &H_0: \ \theta = \theta_0\\ &H_1: \ \theta = \theta_1\end{aligned} \]

似然函数的决策变量

\[ \begin{aligned} &D = \frac{L(\underline x ,\theta_1)}{L(\underline x ,\theta_0)}\end{aligned} \]

拒绝域

\[ \begin{aligned} &N = D = \frac{L(\underline x ,\theta_1)}{L(\underline x ,\theta_0)}>k\end{aligned} \]

※化简

• 对于复杂的比值

\[ \frac{L\left(\underline{X}, \theta_1\right)}{L\left(\underline{X}, \theta_0\right)}=\exp \left[-\frac{1}{2 \sigma^2}\left[\sum_i x_i\left(m_0-m_1\right)+m_0^2+m_1^2\right]>k\right. \]

• 实际上等价于

\[ \sum_i x_i>K \text { dès que } \mathrm{m}_1>\mathrm{m}_0 \]

• 所以接下来只用研究

\[ \alpha=P\left(\bar{X}>k_0 / H_0\right) \]

\[ \beta=P\left(\bar{X}<k / H_1\right) \]

充分统计量

如果(x)是充分统计量，有：

\[ \begin{aligned} &L(\underline x,\theta) = g(t,\theta)h(t)\\ &D = \frac{g(t,\theta_1)}{g(t,\theta_0)}\end{aligned} \]

复合的假设检验 hypothèse composite

假设

\[ \begin{aligned} &H_0 : \ \theta = \theta_0\\ &H_1 : \ \theta \ne \theta_0\\\end{aligned} \]

拒绝域

\[ \begin{aligned} D = \frac{L(\underline{x},\theta_0)}{L(\underline{x},\widehat{\theta})}\end{aligned} \]

假设

\[ \begin{aligned} &H_0: \ \theta < \theta_0\\ &H_1: \ \theta \ge \theta_0\end{aligned} \]

拒绝域

\[ \begin{aligned} D = \frac{L_{H_0}(\underline{x},\widehat{\theta})}{L_{H_1}(\underline{x},\widehat{\theta})}\end{aligned} \]

示例

对于\(F(x)=1-\exp \left(-\frac{x}{a}\right)\)，我们取如下假设：

\[ \begin{aligned}& \mathrm{H}_0: \mathrm{a}_0=800 \mathrm{~m}^3 / \mathrm{an} \\& \mathrm{H}_1: \mathrm{a}_1=1000 \mathrm{~m}^3 / \mathrm{an}\end{aligned} \]

• 通过似然函数法la méthode de Neyman-Pearson寻找决策变量la variable de décision D

\[ \begin{aligned}& \frac{L\left(\underline{X}, a_1\right)}{L\left(\underline{X}, a_1\right)} = \frac{\frac{1}{a_1^n} \exp \left(-\frac{\sum x_i}{a_1}\right)}{\frac{1}{a_0^n} \exp \left(-\frac{\sum x_i}{a_0}\right)}<k\end{aligned} \]

• 等价于：

\[ D=\sum X_i<K \]

• 研究拒绝域

\[ P\left(D>k \mid H_0\right)=\alpha \]

• 由于X是指数分布，可等价于r = 1的gamma分布：

\[ \gamma(1, \lambda) \sim \exp (\lambda) \]

• 因此，D作为gamma分布的线性组合，根据gamma分布的可加性：

\[ D\sim\gamma(n,a), \quad \frac Da\sim \gamma(n,a) \]

• 然后跟据gamma分布和卡方分布的关系：

\[ \frac Da = \chi^2(\frac n2,\frac 12) \]

• 为了方便计算：

\[ \frac {2D}a = \chi^2(n) \]

• 由此，拒绝域：

\[ \begin{aligned}& P\left(\frac{2 D}{a_0}>\frac{2 k}{a_0}\right)=\alpha \\& \frac{2 k}{800}=\chi_{0.05}^2(40) \\& k=22304 \\& D=21360<k, \text { 取 } H_0\end{aligned} \]

• 然后计算第二类错误：

\[ \begin{aligned}\beta & =P\left(D<k \mid H_1\right) \\& =P\left(\frac{2 D}{a_1}>\frac{2 k}{a_1}\right)=0.7\end{aligned} \]

• 然后计算样本数量，使\(\beta<0.5\)
• 由于卡方分布不能反差表，近似到正态分布：

\[ \chi^2(2 n) \rightarrow L G(2 n, \sqrt{4 n}) \]

• 正常计算即可

正态分布的检验

均值的检验,方差已知

单边检验

\[ \begin{aligned} &H_0 : \ m = m_0\\ &H_1 : \ m = m_1>m_0\\\end{aligned} \]

注意拒绝域符号跟m1和m0的大小有关,有:

\[ \begin{aligned} &D = \overline{X}\\ &\mathbf{W:{\overline{X}>K}}\end{aligned} \]

转化为标准正太分布:

\[ \begin{aligned} &P(\overline{X}>k|H_0) = \alpha\\ &P(\frac{\overline{X}-m_0}{\sigma/\sqrt{n}}>\frac{k-m_0}{\sigma/\sqrt{n}})\\ &\Phi(\frac{k-m_0}{\sigma/\sqrt{n}}) = 1-\alpha\\ &\mathbf{k = U_{1-\alpha}\frac{\sigma}{\sqrt{n}}+m_0}\end{aligned} \]

计算第二类错误:

\[ \begin{aligned} \beta =& P(\overline{X}<k|H_1)\\ =&P(\frac{\overline{X}-m_1}{\sigma/\sqrt{n}}>\frac{k-m_1}{\sigma/\sqrt{n}})\\ =&\Phi(\frac{k-m_1}{\sigma/\sqrt{n}})\end{aligned} \]

双边检验

\[ \begin{aligned} &H_0 : \ m = m_0\\ &H_1 : \ m \ne m_0\\\end{aligned} \]

此时两边都是拒绝域,有:

\[ \begin{aligned} &D = \overline{X}\\ &W:{|\overline{X}-m_0|>K}\\ &P(\frac{|\overline{X}-m_0|}{\sigma/\sqrt{n}}>\frac{k}{\sigma/\sqrt{n}})\\&k = U_{1-\alpha/2}\frac{\sigma}{\sqrt{n}}\end{aligned} \]

均值的检验,方差未知

单边

\[ \begin{aligned} &H_0 : \ m = m_0\\ &H_1 : \ m = m_1>m_0\\\end{aligned} \]

有:

\[ \begin{aligned} &\frac{\overline{X}-m_0}{S/\sqrt{n-1}}\thicksim t(n-1)\\ &P(\frac{\overline{X}-m_0}{S/\sqrt{n-1}}>k) = \alpha\\ &k = t_{2\alpha}(n-1)\end{aligned} \]

另一个方向

\[ \begin{aligned} &H_0 : \ m = m_0\\ &H_1 : \ m = m_1<m_0\\\end{aligned} \]

有:

\[ \begin{aligned} &P(\frac{\overline{X}-m_0}{S/\sqrt{n-1}}<k) = \alpha\\ &k = -t_{2\alpha}(n-1)\end{aligned} \]

双边

\[ \begin{aligned} &H_0 : \ m = m_0\\ &H_1 : \ m \ne m_1\\\end{aligned} \]

有:

\[ \begin{aligned} &P(\frac{|\overline{X}-m_0|}{S/\sqrt{n-1}}>k) = \alpha\\ &k = -t_{\alpha}(n-1)\end{aligned} \]

非正态分布的均值

使用中心极限定理可以将这些结果延伸到其他分布上，但仅限于均值

方差的检验,均值已知

已知均值,方差:

\[ \begin{aligned} &D = \frac{1}{n}\sum(X_i-m)^2\\ &\frac{nD}{\sigma^2}\thicksim\chi^2(n)\end{aligned} \]

单边

\[ \begin{aligned} &H_0 : \ \sigma^2= \sigma_0^2\\ &H_1 : \ \sigma^2= \sigma_1^2>\sigma_0^2\\\end{aligned} \]

有

\[ \begin{aligned} \alpha &= P(D>k|H_0)\\ & = P(\frac{nD}{\sigma^2}>\frac{nk}{\sigma^2})\end{aligned} \]

得到

\[ \begin{aligned} &\frac{nD}{\sigma^2} = \chi^2_{\alpha}(n)\\ &k = \chi^2_{\alpha}(n)\frac{\sigma^2}{n}\end{aligned} \]

另一方向

\[ \begin{aligned} &H_0 : \ \sigma^2= \sigma_0^2\\ &H_1 : \ \sigma^2= \sigma_1^2<\sigma_0^2\end{aligned} \]

得到

\[ \begin{aligned} &k = \chi^2_{1-\alpha}(n)\frac{\sigma^2}{n}\end{aligned} \]

双边

\[ \begin{aligned} &H_0 : \ \sigma^2= \sigma_0^2\\ &H_1 : \ \sigma^2= \sigma_1^2\ne\sigma_0^2\\\end{aligned} \]

得到

\[ \begin{aligned} &k_1 = \chi^2_{\alpha/2}(n)\frac{\sigma^2}{n}\\ &D>k_1\\ et \ &k_2 = \chi^2_{1-\alpha/2}(n)\frac{\sigma^2}{n}\\ &D<k_2\\\end{aligned} \]

方差的检验,均值未知

未知均值,方差:

\[ \begin{aligned} &D = S^2\\ &\frac{nD}{S^2}\thicksim\chi^2(n-1)\end{aligned} \]

单边

\[ \begin{aligned} &H_0 : \ \sigma^2= \sigma_0^2\\ &H_1 : \ \sigma^2= \sigma_1^2>\sigma_0^2\\\end{aligned} \]

得到

\[ \begin{aligned} &k = \chi^2_{\alpha}(n-1)\frac{\sigma_0^2}{n}\\ &D>k\end{aligned} \]

比率的检验

双边

\[ \begin{aligned} &H_0: p = p_0\\ &H_1: p \ne p_0\\ &F \rightarrow LG(p,\sqrt{\frac{p(1-p)}{n}})\end{aligned} \]

有:

\[ \begin{aligned} &P(|F-P_0|>k) = \alpha\\ &P(\frac{|F-P|}{\sqrt{p(1-p)/n}}>\frac{k}{\sqrt{p(1-p)/n}}) = \alpha\\ &k = U_{1-\alpha/2}\sqrt{\frac{p_0(1-p_0)}{n}}\end{aligned} \]

使用似然函数的方法

正态分布,单边为例:

\[ \begin{aligned} &H_0 : \ \sigma^2= \sigma_0^2\\ &H_1 : \ \sigma^2= \sigma_1^2>\sigma_0^2\\\end{aligned} \]

似然函数:

\[ \begin{aligned} L(\underline{X},m) &= \prod f(x_i,m)\\ & = \frac{1}{(\sigma\sqrt{2\pi})}exp(-\frac{1}{2\sigma^2}\sum(x_i-m)^2)\end{aligned} \]

似然函数的比值:

\[ \begin{aligned} \frac{L(\underline{X},m_1)}{L(\underline{X},m_0)} &= exp(-\frac{1}{2\sigma^2}(\sum(x_i-m_0)^2-\sum(x_i-m_1)^2)\\ &>k\end{aligned} \]

分布检验 Test d’ajustement

可以使用pdf图判断，也可以根据参数之间的关系来判断

比如期望和方差相等的离散函数，即为泊松分布

图像检验 Ajustement graphique

指数函数和正态分布可以用图像检验

指数分布

对指数分布取ln

\[ \begin{aligned} ln(1-F(x)) = -\lambda x\end{aligned} \]

可见在指数纸上描点画图后，成直线

正态分布

假设有n个点(X1, ..., Xn)都满足正态分布LG(m,σ)

有:

\[ \begin{aligned} u_i = \frac{x_i-m}{\sigma}\end{aligned} \]

在Papier Gausso-arithmétique上,横坐标写每一个点的观察值的上界, 纵坐标写累积的频率, 如果连起来是一个直线, 则说明是正态分布

F= 0.5的值为期望 F = 0.1585和0.8415的位置为方差(也就是图中1的位置)

卡方检验: 离散样本的检验

假设

\[ \begin{aligned} x:&H_0: P(x = x_i) = p_i\\ &H_1: P(x = x_i) \ne p_i\end{aligned} \]

步骤

1. 分组

根据\(*P(x = x_i)*\)分组, 将所有实验样本分为\(*A_1, ..., A_k*\)k组。比如对扔筛子, 进行100次实验, 根据点数分为6组

2. 计算概率

根据假设\(*H_0*\), 计算\(*p_i*\)

3. 确定样本点落在每一组之间个数\(*N_i*\)

统计各组样本的个数, 并作归一化: \(f_i = \frac{N_i}{n}\), 或者使用\(*n ⋅ p_{i}*\)与\(*N_i*\)对应

4. 计算D2

\[ \begin{aligned} D^2 = \sum_{i = 1}^k\frac{(N_i-np_i)^2}{np_i} = n\sum_{i = 1}^k\frac{(\frac{N_i}{n}-p_i)^2}{p_i}\\ L(D^2) = \chi^2_{k-r-1}\end{aligned} \]

• D2满足卡方分布, 卡方分布的自由度\(*k − r − 1*\)中的r是要确定的参数个数, 比如对于正态分布r = 2

5. 检验分组要求\(*np_i*\) ≥ 5

合并临近的分组, 保证\(*np_i ≥ 5*\), 更新\(*L(D_2) = χ_{k − r − 1}^2*\)的k的值

6. 确定risque\(*α*\)

\[ \begin{aligned} &d_0 = \chi^2_\alpha(k-r-1)\\\end{aligned} \]

如果\(*D^2 > d_0*\), 则拒绝假设.

Exemple

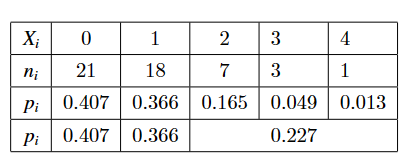
\(*X = [0-21, 1-18, 2-7, 3 -3,  >  = 4-1]*\), 计算得到均值\(0.9\), 方差\(0.97\), 相近, 可能满足泊松分布, 故检验

取泊松分布\(*λ = 0.9*\), 在这里比较接近的取一个好算的即可

查泊松分布表可得, 泊松分布

\(*pi = {0.4066, 0.3659, 0.1647, 0.0494, 1 − 0.4066 − 0.3659 − 0.1647 − 0.0494}*\)

合并\(*np_i < 5*\)的组得到:

\(*p_i = 0 : 0.407, 1 : 0.366,  ≥ 2 : 0.227*\),

得到:

\[ D_2 = \sum_{i = 1}^k\frac{(N_i-np_i)^2}{np_i} \]

\(*k = 3, r = 1, D_2 = 0.033 < χ_{0.052}(3 − 1 − 1)*\)

接收假设

K检验 Test de Kolmogorov

步骤

分组

\[ F_n^* = \left\{\begin{aligned}&0&x<x_1\\&\frac kn&x_k\le x < x_k+1\\&1&x>x_n\end{aligned}\right. \]

在分组后按样本本身排序而非按样本数量分布排序

决策

\[ \begin{aligned} D_n = sup|F(x)-F_n^*|\end{aligned} \]

如果\(*D_n < k*\)，则接受

在下表中，我们假设分布符合指数分布：

\[ \lambda=\frac{1}{\overline x}=\frac{1}{98} \to F(x)=P(X<x)=1-e^{-\lambda x}=1-e^{-\frac{x}{98}} \]

\(x_i\)	8	58	122	133	169
\(F(x_i)\)	0.079	0.447	0.711	0.743	0.821
\(F_i\)	0	0.2	0.4	0.6	0.8
\(|F_i − F(x_i)|\)	0.079	0.247	0.311	0.143	0.021

比较检验

是否来自同一个样本，是否存在显著差异

正态分布的检验

检验σ, m未知

\[ \begin{aligned} &H_0: \sigma_1 = \sigma_2\\ &H_1: \sigma_1 \ne \sigma_2\end{aligned} \]

已知

\[ \begin{aligned} \frac{nS^2}{\sigma^2}\thicksim\chi^2_{n-1}\end{aligned} \]

使用\(D = \frac{S_1^2}{S_2^2}\)左右判别函数

使用

\[ \begin{aligned} k_0 = \frac{\frac{n_1S_1^2}{n_1-1}}{\frac{n_2S_2^2}{n_2-1}} \thicksim F(n_1-1,n_2-1)\end{aligned} \]

如果D < k0,接受

检验m, σ未知

使用:

\[ \begin{aligned} D = \frac{(\bar x_1 - \bar x_2)-(m_1-m_2)}{\sqrt{(n_1S_1^2+n_2S_2^2)(1/n_1+1/n_2)}}\sqrt{n_1+n_2-2}\\\thicksim t(n_1+n_2-2)\\ k = t_\alpha(n_1+n_2-2)\end{aligned} \]

一般应用

比较六个小班的学习成绩分布是否没有显著差异，样本数为6

取形态：100-90分，90-80分，80-70分，70-60分，60-分

统计不同样本落在不同形态的个数

	M1	M2	M...	Mr	total
E1	n11	n12	n1, …	n1r	n1.
E2	n21	…		n2r	n2.
E...	n…, 1			n…, r	n…, .
Ek	nk1	nk2	nk, …	nkr	nk.
total	n.1	n.2	n., …	n.r	nkr

判别：

\[ \begin{aligned} d_0^2 &= \sum_{i = 1}^{k}\sum_{j = 1}^{r}\frac{(n_{ij}-n_{i.}P_i)^2}{n_{i.}p_j}\\ & = \sum_{i = 1}^{k}\sum_{j = 1}^{r}\frac{(n_{ij}-n_{i.}\frac{n_{.j}}{N})^2}{n_{i.}\frac{n_{.j}}{N}}\\ & = N((\sum_{i = 1}^{k}\sum_{j = 1}^{r}\frac{n_{ij}^2}{n_{i.}n_{j.}})-1)\end{aligned} \]

k:

\[ \begin{aligned} k = \chi^2_{\alpha}(kr-k-(r-1)) = \chi^2_{\alpha}(k-1)(r-1)\end{aligned} \]

两个样本的比较

样本：\(*E_1, E_2*\), 假设\(*H0: P1 = P2 = P; H1: P1\ne P_2*\)

百分比的检验

\[ \begin{aligned} &p\thicksim\widehat p = \frac{n_1f_1+n_2f_2}{n_1+n+2}\\ &F_1\thicksim LG(p,\sqrt{\frac{p(1-p)}{n_1}})\\ &F_2\thicksim LG(p,\sqrt{\frac{p(1-p)}{n_2}})\\ &F_1-F_2\thicksim LG(0,\sqrt{p(1-p)(1/n_1+1/n_2)})\\ &k = U_{1-\alpha/2}\\ &D = \frac{f_1-f_2}{\sqrt{p(1-p)\sqrt{1/n_1+1/n_2}}} &\text{拒绝域}: D>k\end{aligned} \]

卡方检验

	M1	M2
E1	a	b	a+b
E2	c	d	c+d
	a+c	b+d

\[ \begin{aligned} &D^2 = N\frac{(ad-bc)^2}{(a+b)(a+c)(b+c)(b+d)}\thicksim\chi^2(1)\\ &k = \chi^2_{\alpha}(1 )\end{aligned} \]