分布和近似
分布和近似
文档详细讨论了正态分布、卡方分布、F分布和T分布的定义、性质和期望与方差。正态分布的独立线性组合满足正态分布,卡方分布的期望值等于其自由度,方差则为自由度的两倍。F分布用于检验模型中的各项效应是否显著,而T分布在样本量较小的情况下,相较于正态分布,更为稳健。
此外,还讨论了从超几何分布到二项分布、从二项分布到泊松分布、从正态分布到标准正态分布、从二项分布到正态分布、从泊松分布到正态分布和从卡方分布到正态分布的近似。
分布
均匀分布 Loi uniform
discret
\[ \begin{aligned} & X(\Omega) = {1, 2, ..., n}\\ & P(X = k) = \frac{1}{n}\\ & E(X) = \frac{n+1}{2}\\ & V(X) = \frac{n^2-1}{12}\end{aligned} \]
continue sur [0, a]
\[ \begin{aligned} & f(x) = 1/a \mathcal{X}_{[0, a]}\\ & E(x) = a/2\\ & V(x) = a^2/12\end{aligned} \]
continue sur [a,b]
\[ f(x) = 1/(b-a)\chi_{[a,b]}\\F(x) = \frac {x-a}{b-a}\chi_{[a,b]}\\E(x) = \frac{a+b}{2}\\V(x) = \frac{(b-a)^2}{12} \]
零一分布 Loi de Bernoulli
仅discret
\[ \begin{aligned} & X(\Omega) = {0, 1}\\ & P(X = 1) = p\\ & P(X = 0) = 1-p\\ & E(X) = p\\ & V(X) = p(1-p)\end{aligned} \]
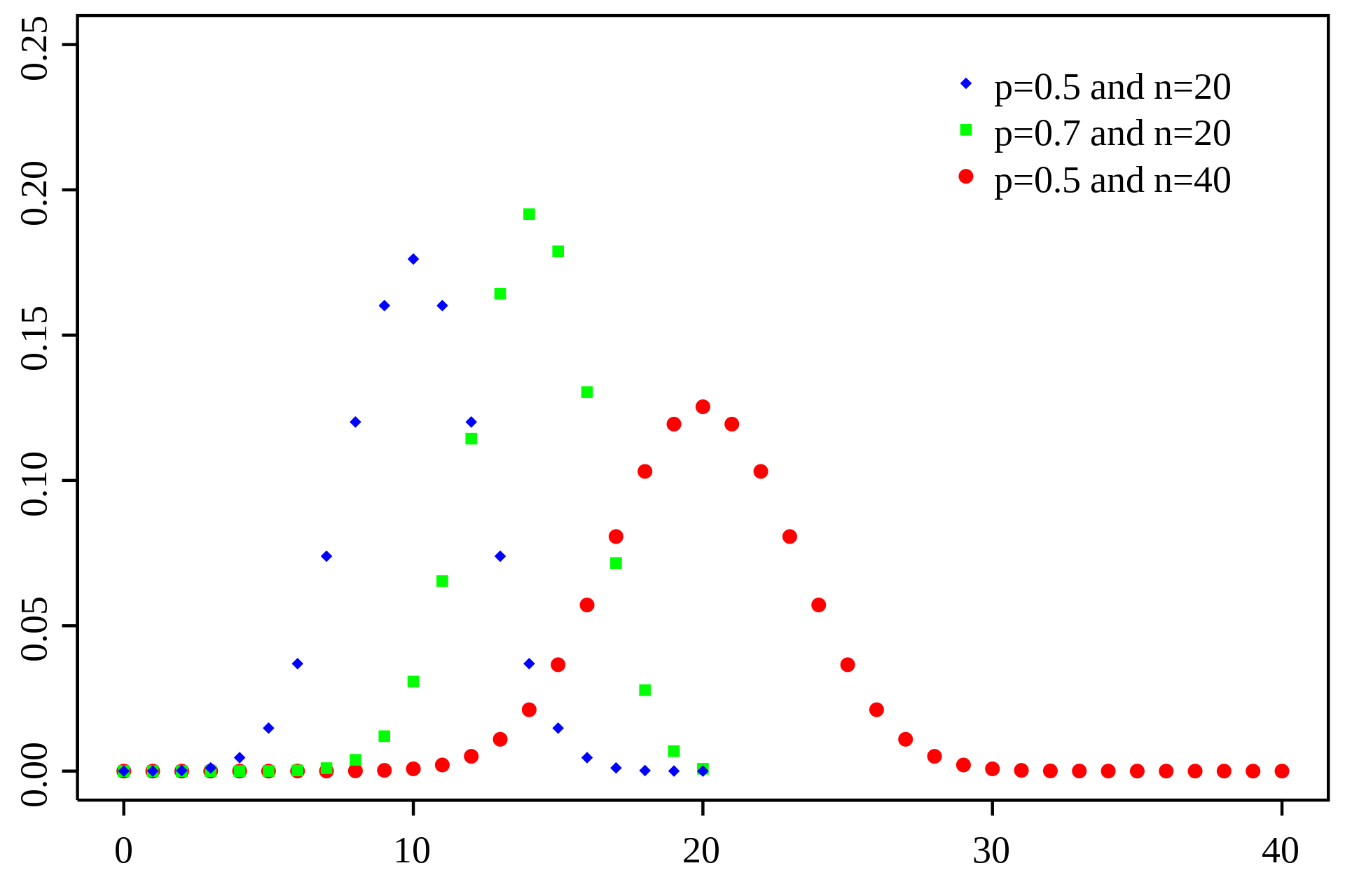
二项分布 B(n, p)
二项分布是一种离散概率分布。它描述了在一定数量的独立试验中,成功的次数的概率分布。每次试验都有两种可能的结果:成功或失败。并且每次试验成功的概率是相同的。
仅discret
\[ \begin{aligned} & X(\Omega) = {0, 1, ...}\\ & P(X = k) = C_n^kP^k(1-p)^{n-k}\\ & E(X) = np\\ & V(X) = np(1-p)\end{aligned} \]
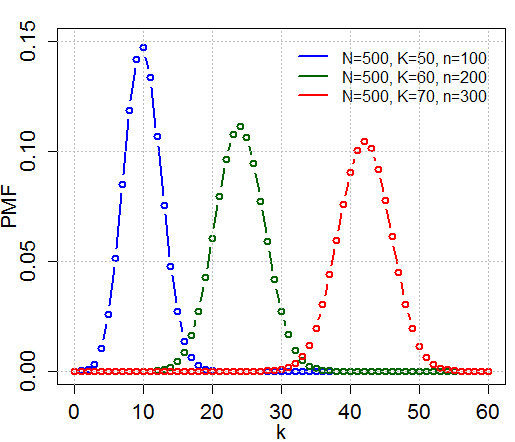
超几何分布 H(N, n, p)
N个样本中,其中不合格数据的真实概率为p。超几何分布描述了在N个样本中抽出n个,有k个不合格的概率。
仅discret
\[ \begin{aligned} & X(\Omega) = {0, 1, ...}\\ & P(X = k) = \frac{\tbinom{Np}{k}\tbinom{N-Np}{n-k}}{\tbinom{N}{n}}\\ & E(X) = np\\ & V(X) = np(1-p)\frac{N-n}{N-1}\end{aligned} \]
例子
On a bagué 200 flamants roses vivant sur un lac qui en compte 40 000. Pour étudier cette colonie, on en capture 100.
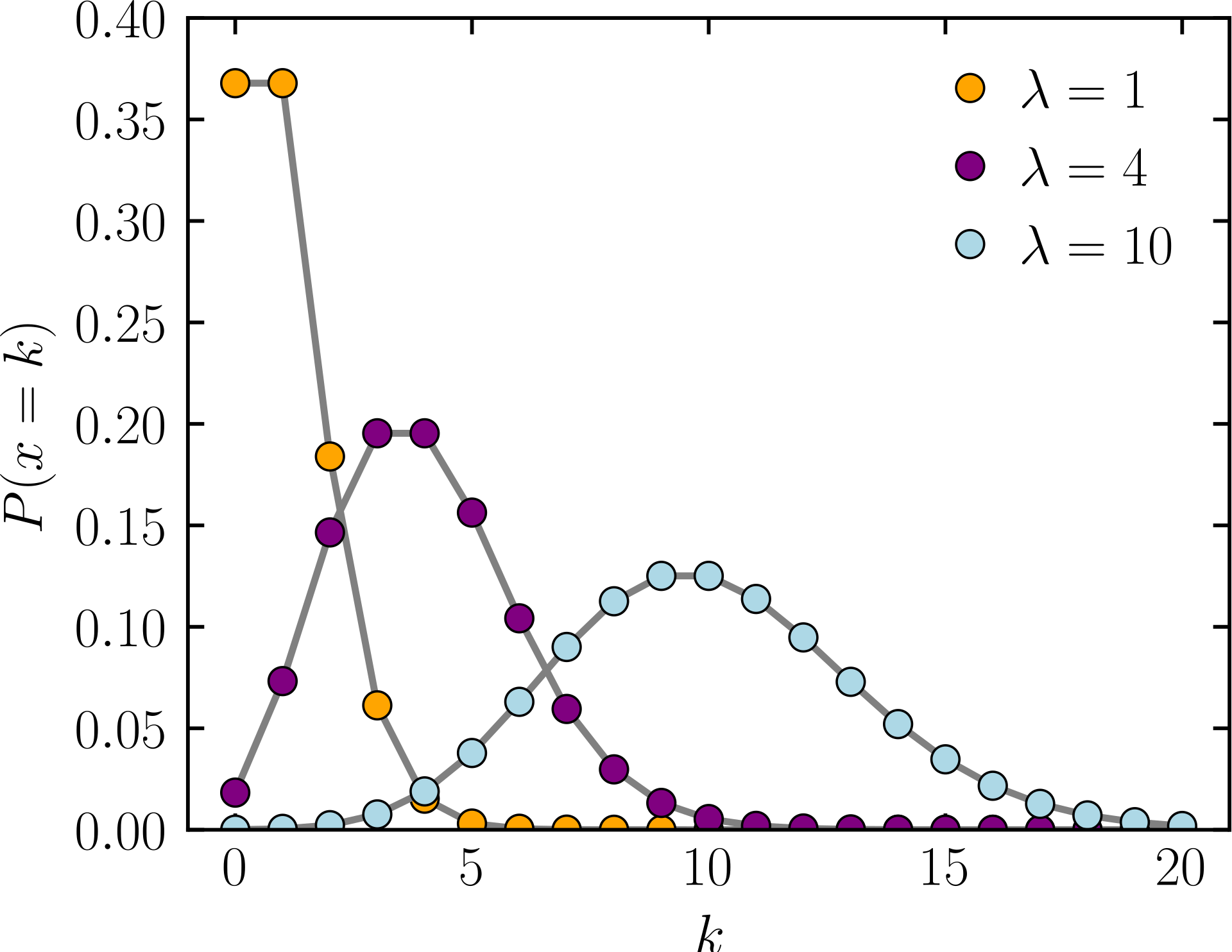
泊松分布 P(λ)
泊松分布是一种离散概率分布,它表示在一定时间或空间范围内,某事件发生的次数的概率分布
仅discret
\[ \begin{aligned} & X(\Omega) = {0, 1, ...}\\ & P(X = k) = \frac{e^{-\lambda}\cdot\lambda^k}{k!}\\ & E(X) = \lambda\\ & V(X) = \lambda\end{aligned} \]
指数分布 Loi exponentielle
指数分布是一种连续概率分布,通常用于描述在固定时间或空间范围内,某事件发生的次数的概率分布。它的概率密度函数为 \(f(x) = \lambda e^{-\lambda x}\),其中 \(\lambda > 0\) 是事件发生的平均速率,\(x \geq 0\)。其期望一般代表平均寿命。
指数分布具有无记忆性,即无论过去已经等待多久,从现在开始再等待某个时间的概率仍然不变。
此外,指数分布是唯一具有无记忆性的连续分布,对于连续随机变量,只有指数分布具有无记忆性。

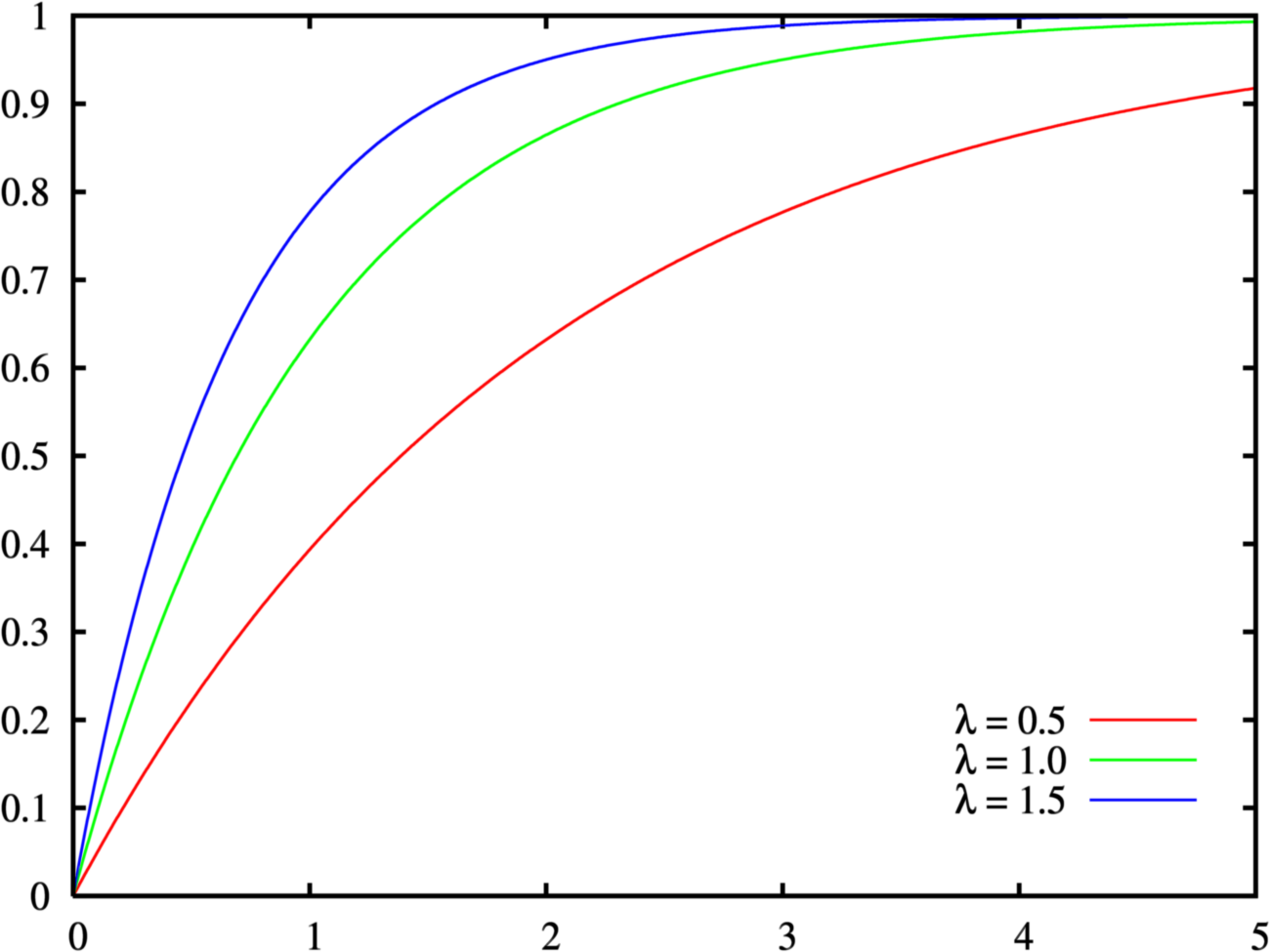
continue
\[ \begin{aligned} & f(x) = \left\{ \begin{aligned} &\lambda e^{-\lambda x} & x>0\\ &0&x\le0\ \end{aligned} \right.\\ & F(x) = \left\{ \begin{aligned} &1-e^{-\lambda x}&x>0\\ &0&x\le0 \end{aligned} \right.\\ & E(x) = 1/\lambda\\ & V(x) = 1/\lambda^2\end{aligned} \]
无记忆性
指数分布具有无记忆性的特点, \(*P(x > t_0 + t|x > t_0) = P(X > t)*\), 于t0无关。
\(\begin{aligned} P(x>t_0+t|x>t_0) &= \frac{P(x>t_0+t)}{P(x>x_0)} \\ &= \frac{1-F(t_0+t)}{1-F(t_))}\\ &= e^{-\lambda t} \\ &= P(X>t)\end{aligned}\)
Gamma分布 γ(r, λ)
Gamma分布是一种连续概率分布,常用于描述等待多个独立随机事件发生所需时间的概率分布。如果一个随机变量X服从参数为λ的指数分布,且需要等待r个独立事件的发生,那么总等待时间则服从参数为r和λ的Gamma分布。
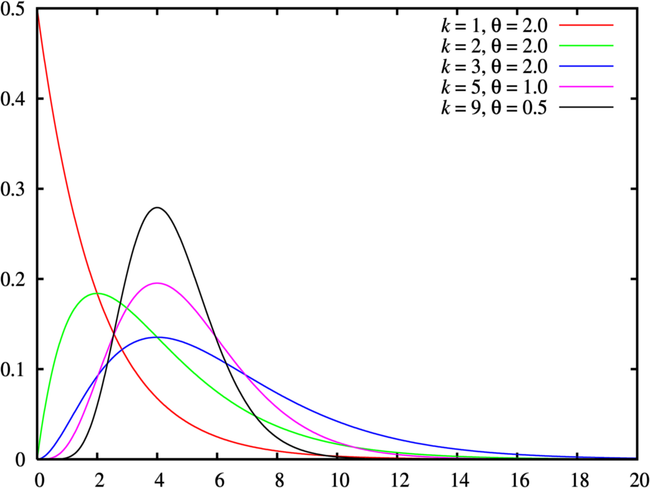
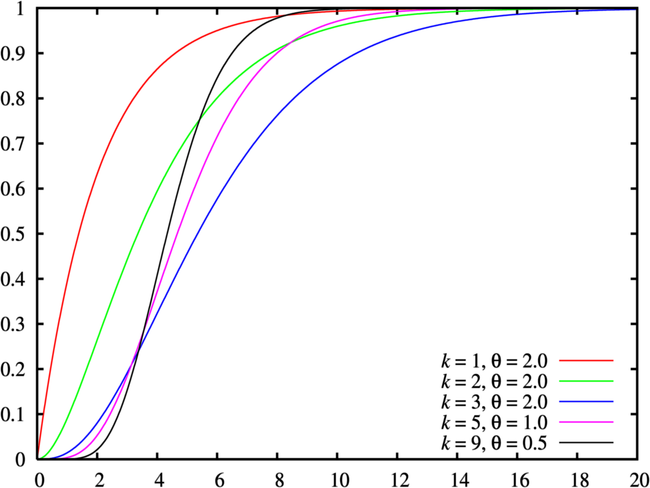
欧拉函数:
\[ \begin{aligned} &\Gamma(r) = \int^{+\infty}_0e^{-y}y^{r-1}dy\\ &\Gamma(r) = (r-1)\Gamma(r-1)\\ &\Gamma(n) = (n-1)!\end{aligned} \]
continue
\[ \begin{aligned} & f(x) = \frac{\lambda^r}{\Gamma(r)}e^{-\lambda x}x^{r-1}&X>=0\\ & E(x) = \frac{r}{\lambda}\\ & V(x) = \frac{r}{\lambda^2}\end{aligned} \]
期望推导:
\[ \begin{aligned} E(x) &= \int_0^{\infty} x^re^{-rx}\frac{\lambda^r}{\Gamma(r)}dx\\ & =\frac{1}{\Gamma(r)}\int_0^{\infty}(\lambda x)^re^{-rx}dx\\ & =\frac{1}{\lambda \Gamma(r)} \int_0^{\infty}u^r e^{-u}du\\ & = \frac{\Gamma(r+1)}{\lambda \Gamma(r)}\\ & = \frac{r}{\lambda}\end{aligned} \]
Gamma的可加性
当两随机变量服从Gamma分布,且相互独立,且参数相同时,Gamma分布具有可加性。
\[ \coprod\left\{\begin{array}{l}r . v . X \sim \gamma\left(\alpha_1, \lambda\right) \\r . v . Y \sim \gamma\left(\alpha_2, \lambda\right)\end{array} \Longrightarrow X+Y \sim \gamma\left(\alpha_1+\alpha_2, \lambda\right)\right. \]
gamma的近似线性
\[ X \sim \gamma(r, \lambda) \rightarrow \lambda*X \sim \gamma(r) \]
特殊情况:γ(r) : λ = 1
- 期望等于方差
\[ E(x) = r = V(X) \]
r = 1时, 指数分布和gamma分布等价:\(\gamma(1, \lambda) \thicksim exp(\lambda)\)
正态分布 LG()
正态分布,也被称为高斯分布,其形状由两个参数决定:均值(m)和标准差(σ)。均值决定了分布的中心位置,标准差决定了分布的宽度和尖峰的高度。是概率中应用上最重要的分布
被称为正态分布(\(*N(m, σ^2)*\))或者拉普拉斯-高斯分布(\(*LG(m, σ)*\)), 注意这里定义上的区别, 其概率密度函数和分布函数为:
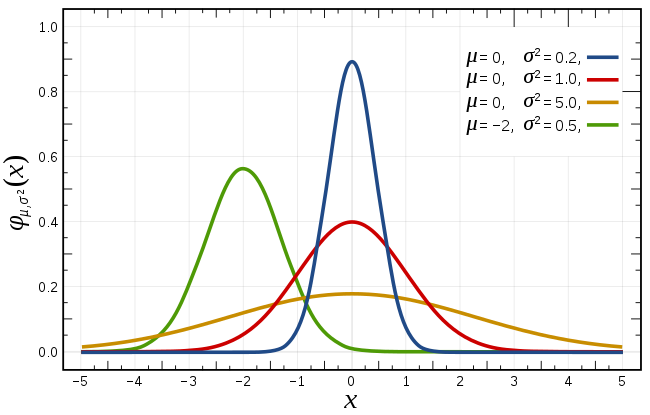
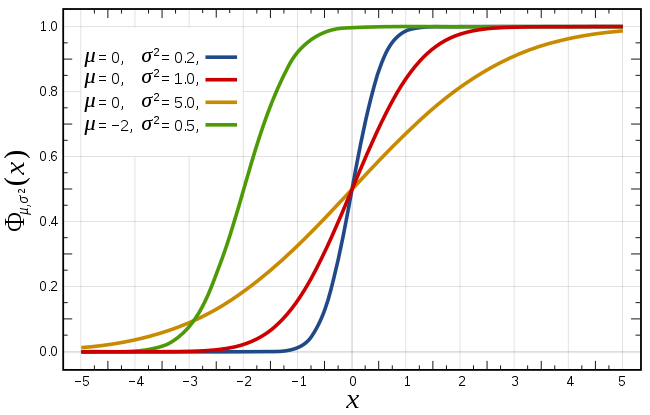
正态分布:LG(m, σ)
\[ \begin{aligned} & f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-m}{\sigma})^2}\\ & F(x) = \frac{1}{\sigma\sqrt{2\pi}}\int^x_{-\infty}e^{-\frac{1}{2}(\frac{x-m}{\sigma})^2}dt\end{aligned} \]
标准正太分布: U
\[ \begin{aligned} & U \thicksim LG(0, 1)\\ & \phi(u) = \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}u^2}\\ & \Phi(u) = \frac{1}{\sqrt{2\pi}}\int^x_{-\infty}e^{-\frac{1}{2}u^2}du\\\end{aligned} \]
- 通过查表6, 7可计算标准正太分布,
表6根据
u查$*ϕ(u)*$, 表7根据*Φ*(*u*)查u, 其中表7上和左标签相互对应, 下和右标签相互对应, 如果Φ(u) < 0.5结果需要是负数, 也就是使用上和左标签, 则为负数, 若使用右和左标签, 则使用正数。需要查表原因是正态分布不能使用符号计算解出
正态分布和标准正态分布
正态分布和标准正态分布可以互相转换:
\[ x \thicksim LG(m, \sigma) \Leftrightarrow u = \frac{X-m}{\sigma} \thicksim LG(0, 1) \]
做题时要写出
\[ \begin{aligned} F(x) &= P(X<x) = P(\frac{X-m}{\sigma}<\frac{x-m}{\sigma})\\ &= P(U<\frac{x-m}{\sigma}) = \Phi(\frac{x-m}{\sigma})\end{aligned} \]
具体证明过程参考近似章的相应章节
其期望和方差分别为:\(*E(x) = m, V(x) = σ^2*\), 期望和方差的推导如下:
\(\begin{aligned} E(x) &= \frac{1}{\sigma\sqrt{2\pi}}\int^{+\infty}_{-\infty}xe^{-\frac{1}{2}(\frac{x-m}{\sigma})^2}dt\\ & = \frac{1}{\sqrt{2\pi}}\int^{+\infty}_{-\infty}(\sigma t+m)e^{-\frac{t^2}{2}}dt \ t = \frac{x-m}{\sigma}\\ & = \frac{\sigma}{\sqrt{2\pi}}\int^{+\infty}_{-\infty}te^{-\frac{t^2}{2}}dt \ [=0] + \frac{m}{\sqrt{2\pi}}\int^{+\infty}_{-\infty}e^{-\frac{t^2}{2}}dt \ \\ & = m*\int^{+\infty}_{-\infty}\frac{1}{\sqrt{2*\pi}}e^{-\frac{t^2}{2}}dt \ [m\Phi(\infty)]\\ & = m\\ V(x) &=E(X-m)^2\\ & = \frac{1}{\sigma\sqrt{2\pi}}\int^{+\infty}_{-\infty}(x-m)^2e^{-\frac{1}{2}(\frac{x-m}{\sigma})^2}dt\\ & = \frac{\sigma^2}{\sqrt{2*\pi}}\int^{+\infty}_{-\infty}t^2e^{-\frac{t^2}{2}}dt\\ & = -\frac{\sigma^2}{\sqrt{2*\pi}}te^{1\frac{t^2}{2}}\mid^{+\infty}_{-\infty}+\frac{\sigma^2}{\sqrt{2*\pi}}\int^{+\infty}_{-\infty}e^{-\frac{t^2}{2}}dt\\ & = \sigma^2\end{aligned}\)
正态分布的性质
- 正态分布的独立线性组合满足正态分布:
\[ \begin{aligned} &X\thicksim LG(m_1, \sigma_1), \ Y\thicksim LG(m_2, \sigma_2) \ \\ &X+Y \thicksim LG(m_1+m_2, \sqrt{\sigma_1^2+\sigma_2^2})\end{aligned} \]
独立正态分布的均值满足正态分布且若所
有的*Xi*同分布$X_i\thicksim LG(m, \sigma)$, 则均值$\overline{X} = LG(m, \frac{\sigma}{\sqrt{n}})$, 很简单的由1可推出若\(*U = LG(0, 1)*\), 则有\(Z = \frac{U^2}{2}\thicksim\gamma(1/2)\)
高斯向量
高斯向量,也称为正态向量,是一个多元随机变量向量,其任何线性组合都遵循正态分布。如果一个随机向量中的所有元素都服从一元正态(高斯)分布,且任何这些元素的线性组合也服从正态分布,那么这个随机向量就是高斯向量。
如果向量X是高斯向量, 则X = (x1, x2, ..., xn)中所有线性组合都是正态分布
卡方分布 Loi du χ2
卡方分布(Chi-squared distribution)是统计学中常用的一种概率分布。在卡方检验中,卡方分布是一种特殊的伽玛分布。当独立的标准正态随机变量的平方和服从卡方分布。卡方分布的期望值等于其自由度,方差则为自由度的两倍。卡方分布广泛用于假设检验和置信区间的构造等统计推断方法中。
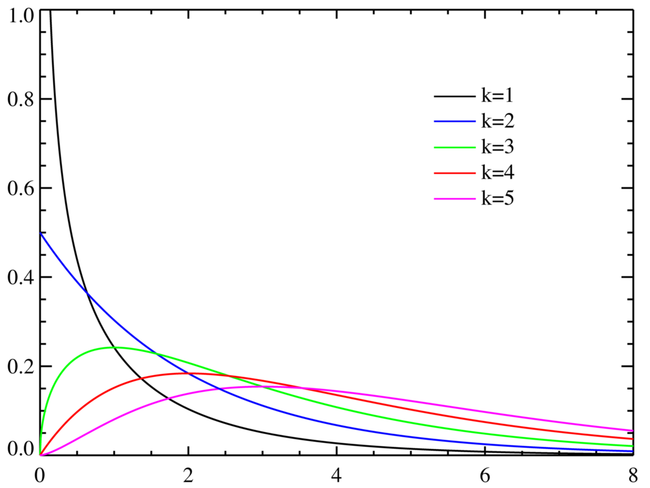
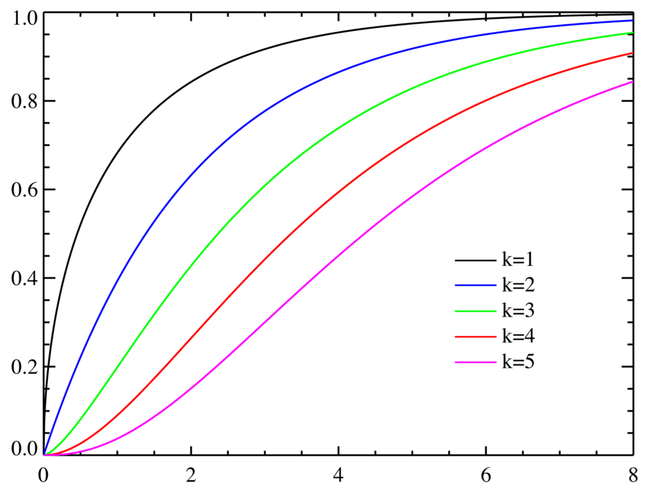
定义
\((X1, X2, ..., Xn)\)独立
\(X_i \thicksim LG(0, 1)\)
则有:
\[ \chi^2_n = \sum_{i = 1}^{n}X_i^2 \]
\[ \begin{aligned} &g(u) = \frac{1}{2^{\frac{n}{2}}\Gamma(\frac{n}{2})}e^{-\frac{n}{2}}u^{\frac{n}{2}-1}\\ &\chi^2_n \Leftrightarrow \gamma(\frac{n}{2}, \frac{1}{2})\end{aligned} \]
不同n的情况下的卡方分布, 可以看到n在较大的时候近似于高斯分布
期望和方差
期望和方差可以直接有伽马分布得出
\[ \begin{aligned} &E(X) = n\\ &V(X) = 2n\end{aligned} \]
性质
- 如果\(X \sim LG(0,1)\),则\(X^2\sim\chi^2(1)\)
- 如果 \(\chi^2_n \thicksim X\) 且 \(\chi^2_p \thicksim Y\), 则有 \(\chi^2_{n+p} \thicksim X+Y\), 当 \(*X = Y*\) 时, 有 \(2X \thicksim \chi^2_{2n}\)
卡方分布在n无穷大时可以近似于高斯分布, 参考近似部分
F分布 Fisher-Snedecor
F分布,又称为费舍尔-斯内德科尔分布或者费舍尔分布,是一种连续概率分布。在方差分析和回归分析中,F统计量经常用于检验模型中的各项效应是否显著。特别的,F分布可以用来进行两个正态总体的方差是否相等的假设检验。
F分布的形式由两个参数来决定,通常被记作F(n, p),其中n,p是自由度。具体来说,如果随机变量X服从卡方分布且自由度为n,Y也服从卡方分布且自由度为p,且X和Y是独立的,那么\(F=\frac{X/n }{ Y/p}\) 就服从F分布,记作F(n, p)。
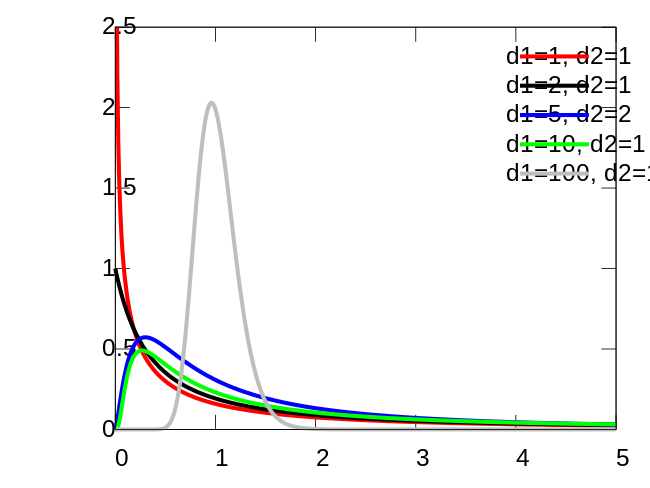
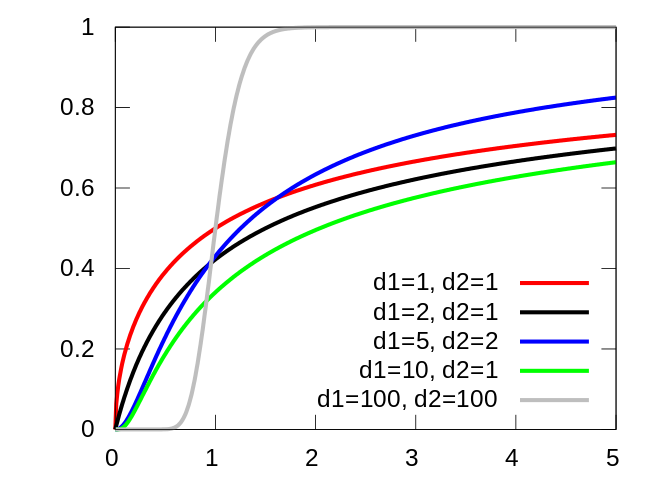
定义
F分布:
\[ \begin{aligned} &X \thicksim \chi^2_n \ \ \ Y \thicksim \chi^2_p\\ &F(n, p) = \frac{X/n}{Y/p} = Z\end{aligned} \]
期望和方差
- 期望
\[ E(X) = \frac{p}{p-2} \]
- 方差
\[ V(X) = \frac{2p^2(n+p-2)}{n(p-2)^2(p-4)} \]
性质
若\(Z\thicksim F(n, p)\), 则\(\frac{1}{Z} \thicksim F(p, n)\)
\(*F_{m, n(1 − α)} = 1/F_{n, m(α)}\)* 以用于查表
T分布 student
T分布,也被称为学生t分布,是用于小样本数据的假设检验和区间估计等统计推断中的一种重要的连续概率分布。它在样本量较小的情况下,相较于正态分布,更为稳健。
如果一个随机变量X服从标准正态分布,另一个随机变量Y服从卡方分布且自由度为n,且X和Y是独立的,那么\(Z = X / \sqrt{(Y/n)}\)就服从自由度为n的t分布。
定义
T分布:
\[ \begin{aligned} &X \thicksim LG(0, 1) \ \ \ y \thicksim \chi^2_n \ \ \ X, \ Y \ indépendant\\ &T(n) = \frac{X}{\sqrt{Y/n}}\end{aligned} \]
期望和方差
\[ E\left(T_n\right)=0 \quad V\left(T_n\right)=\frac{n}{n-2} \]
性质
- n趋于无穷时, T分布趋于正态分布\(\mathrm{n} \rightarrow+\infty \quad T_n \rightarrow L G(0,1)\)
- T分布和F分布有一定关系:\(T_n^2 \thicksim F(1, n)\)
近似
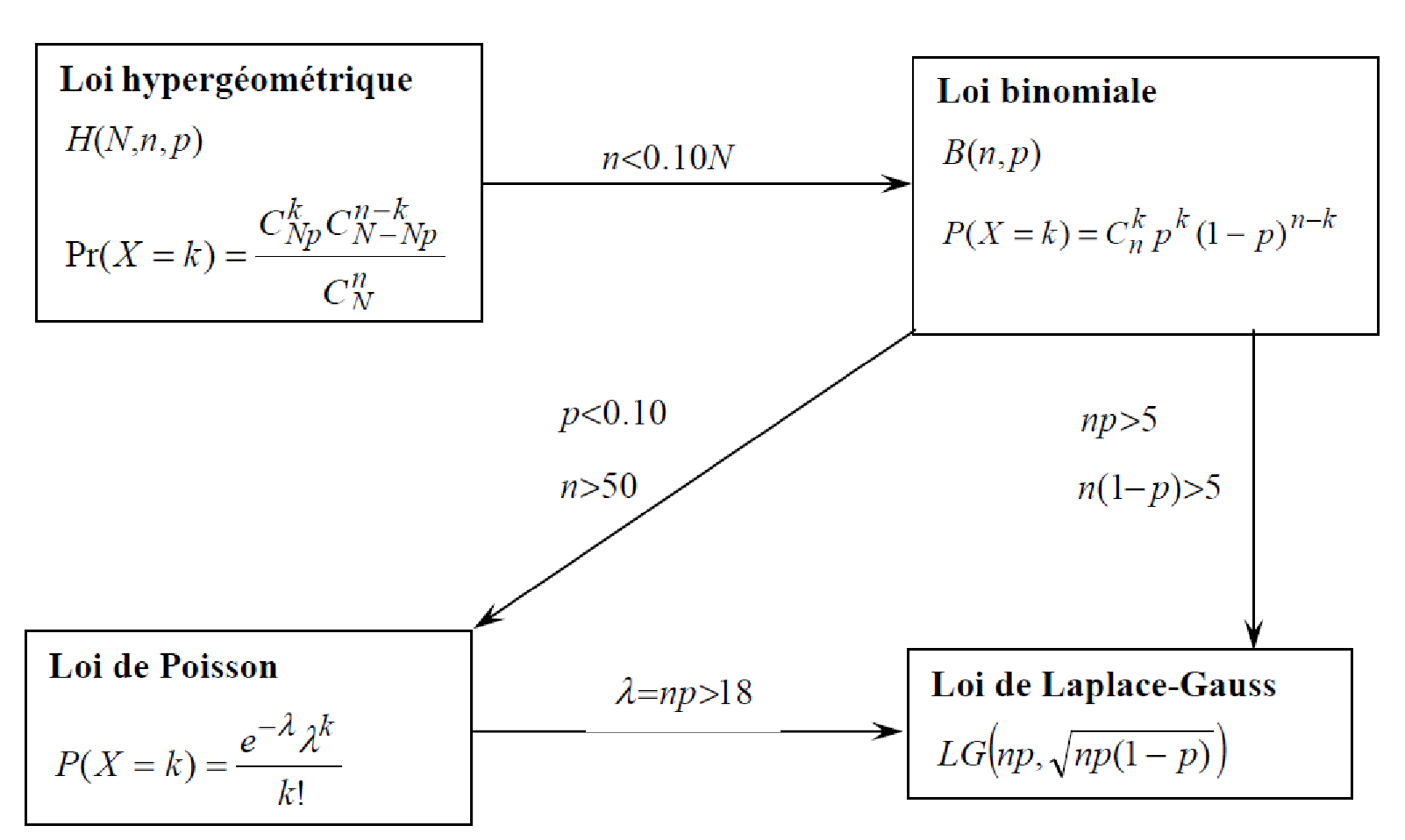
从超几何分布到二项分布
要求 *n*/*N* ≤ 10%
\(*H(N, n, p) → B(n, p)*\)
\[ P(X = x) = \frac{C_{Np}^xC_{N-Np}^{n-x}}{C_{N}^{n}} \thicksim C_n^xp^x(1-p)^{n-x} \]
从二项分布到泊松分布
要求
*n* > 50 *p* < 0.1 *np* = *λ*
\(*B(n, p) → P(λ)*\)
\(P(X = x) = C_n^{x}p^{x}(1-p)^{n-x}\thicksim\frac{\lambda^x}{x!}e^{-\lambda}\)
从正态分布到标准正态分布(非近似)
正态分布和标准正态分布可以互相转换:
\[ x \thicksim LG(m, \sigma) \Leftrightarrow u = \frac{X-m}{\sigma} \thicksim LG(0, 1) \]
证明过程如下:
\(\begin{aligned} P(U\le u) &= P(\frac{X-m}{\sigma}<u) \\ & = P(X<\sigma u+m)\\ & = \int_{\infty}^{\sigma u+m}\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{t-m}{2\sigma}}dt\\ & = \int_{\infty}^{u}\frac{1}{\sqrt{2*\pi}}e^{-\frac{s^2}{2}}ds\\ & = \Phi(S) F(x) &= P(X<x) \\ &= P(\frac{X-m}{\sigma}<\frac{x-m}{\sigma}) \\ &= P(U<\frac{x-m}{\sigma}) \\ &= \Phi(\frac{x-m}{\sigma})\end{aligned}\)
从二项分布到正态分布: 莫瓦尔-拉普拉斯定理
莫瓦尔-拉普拉斯定理,也被称为二项式分布的中心极限定理,是概率论中的一个重要定理。该定理表明,当二项式分布的试验次数趋向无穷大时,二项式分布可以近似为正态分布。它是中心极限定理的一个特例。
二项分布可以由正态分布近似:
\[ B(n, p) \rightarrow LG(np, \sqrt{np(1-p)}) \]
条件
\[ np > 5, n(1 − p) > 5 \]
从泊松分布到正态分布
\(P(\lambda) \rightarrow LG(\lambda, \sqrt{\lambda})\)
条件:*λ* > 18
由于泊松分布本身比较好算, 所以用处有限
一般是用于在λ过大, 导致表里没有的时候才会如此近似
从卡方分布到正态分布
卡方分布在n足够大时近似于正态分布 \(\chi^2(n) \xrightarrow{n\rightarrow \infty} LG(n, \sqrt{2n})\)
证明
设\(T_i = \frac{1}{2}X_i^2\), 有\(\chi^2 = 2\sum T_i\)
其中, \(T_i \thicksim \gamma_\frac{1}{2}\), 故有\(E(T_i) = 1/2 \ V(T_i) = 1/2\)
应用中心极限定理:
\[ \begin{align*} &\frac{\sum T_i-\frac{1}{2}n}{\sqrt{1/2}\sqrt{n}} \rightarrow LG(0, 1)\\ &\frac{2\sum T_i-n}{\sqrt{2n}} \rightarrow LG(0, 1)\\ &\chi^2_n \rightarrow LG(n, \sqrt{2n}) \end{align*} \]