概率基础
概率基础
概率基础涵盖了期望、方差、切比雪夫不等式、多元随机变量(离散和连续)、随机变量的收敛(依概率收敛、平方平均收敛、\(L^p\)收敛、依分布收敛)、莫瓦尔-拉普拉斯定理、大数定理和中心极限定理等主题。这些主题详细解释了随机变量的各种性质和定理,包括期望和方差的计算,二项分布的正态分布近似,以及随机变量序列的收敛性。
概率和随机变量
概率空间 (Ω, C, P)
概率空间是测度论中的一个基本概念,它是一个包含样本空间、事件和概率测度的三元组。在概率论中,我们通常把它定义为一个三元组(Ω, F, P),其中:
- Ω是样本空间,代表所有可能的结果的集合。
- F是事件场或σ-代数,包含了样本空间的子集,这些子集被认为是"发生"或"不发生"的事件。简单来说,它是样本空间的一个子集族。
- P是概率测度,为每一个事件赋予一个实数,表示该事件发生的概率。这个函数需要满足一些基本的性质,例如非负性、规范性和可列可加性。
条件概率
条件概率是在给定某个事件发生的情况下,另一个事件发生的概率。这被表示为P(A|B),读作“在B发生的条件下A发生的概率”。其公式为:
\[ \\P(A|B) = \frac{P(A \cap B)}{P(B)} \]
独立性
- \(*P(A|B) = P(A)*\)
全概率公式
Probabilisé Totales:
- \(\\P(A) = \sum_{i = 1}^{n}P(B_i)P(A|B_i)\)
贝叶斯公式
Formules de Bayes:
- \(\\P(B_i|A) = \frac{P(A|B_i)P(B_i)}{\sum_k[P(A|B_k)P(B_k)]}\)
实际上, 分母即为全概率公式,因此更常用的公式形式为
- \(P(B|A) = \frac{P(A|B)P(B)}{P(A)}\)
随机变量
随机变量是将样本空间的每个可能的结果映射到实数线上的函数。\((\omega, C, P)\to(R, B)\)
概率分布
概率分布是一个定义在一个样本空间上的函数,它给出了样本空间中每一个事件发生的概率。
\(*P_X(B) = P[X^{−1}(B)]*\)
累计分布
累积分布函数(简称CDF)是一种描述一个实数随机变量概率分布的函数。这个函数对于随机变量X中小于或等于某个特定值的概率进行描述。
\(*F(x) = P(X < x)*\)
\(F(b)-F(a)=P(a \leq X<b)\)
概率质量函数
概率质量函数(probability mass function,简称PMF)是离散随机变量在各特定取值上的概率。
\[ \begin{aligned} &p_i = P(X = x_i)\\ &F(x) = P(X<x) = \sum_{x_i<x}P_i\end{aligned} \]
概率密度函数
概率密度函数(probability density function,简称PDF)是连续随机变量在各特定取值上的概率。
\[ \begin{equation*} F(X) = \int_{-\infty}^{x}f(x)dx\end{equation*} \]
其中, f代表概率密度函数
随机变量的函数 Loi de Y = θ(X)
双射函数
\(\begin{aligned} &\theta \ est \ bijective\\ &\uparrow G(y) = G(\theta(X)<y) = F(X<\theta^{-1}(y)) = F(\theta^{-1}(y))\\ &\downarrow G(y) = G(\theta(X)<y) = F(X>\theta^{-1}(y)) = 1-(\theta^{-1}(y)) \\ \end{aligned}\)
其他函数
$$ \[\begin{aligned} &\theta \ est \ quelconque\\ &Exemple\\ &G(y) = P(X^2<y) = P(-\sqrt{y}<x<\sqrt{y}) = F(\sqrt{y})-F(-\sqrt{y})\end{aligned}\]$$
期望, 方差和不等式
这一章主要介绍了关于期望、方差和不等式的基本概念和定理。
- 期望是随机变量的平均值,或者说是随机变量可能取值的加权平均,权重是每个值的概率。
- 方差则是衡量随机变量离散程度的一种方式,即随机变量的取值与其期望值的偏差的平方的期望。
- 切比雪夫不等式则给出了随机变量的取值落在其平均值一定范围内的概率下界。
- 此外,还介绍了期望和方差的一些性质,如期望的线性性质,方差的计算公式等,并引入了协方差和相关系数这两个用于描述两个随机变量之间关系的量。
期望
\[ \begin{aligned} &variable\ discrete\ E(X) = \sum_ix_iP(X = x_i)\\ &variable\ continue\ E(X) = \int_axf(x)dx\end{aligned} \]
centrée
期望为0
独立的期望
\[ E(XY) = E(X)E(Y) \]
方差
\(\begin{aligned} &V(X) = E[(X-m)^2]\\ &V(X) = E(X^2)-[E(X)]^2\end{aligned}\)
réduite
方差为1
独立的方差
\[ var(X + Y) = var(X) + var(Y) \]
切比雪夫不等式
Bienaymé-Tchebychev不等式
切比雪夫不等式是概率论中的一个基本不等式。它给出了随机变量的取值落在其平均值一定范围内的概率下界。具体来说,对于任何大于零的k,切比雪夫不等式表明一个随机变量的取值落在其平均值加减k倍标准差的范围内的概率至少为1-1/k²。这个不等式对于所有的随机变量都成立,无论它们的概率分布是什么样的。
\[ \begin{gathered}P(|X-E(X)|>k \sigma) \leq \frac{1}{k^2} \\P(|X-E(X)|>k) \leq \frac{\sigma^2}{k^2}\end{gathered} \]
这里的E(X)代表随机变量X的期望(或平均值),σ是X的标准差,k是任何大于零的实数。
多元随机变量
多元随机变量:离散
联合分布和边缘分布
- 联合分布 \(*P_{ij} = p(X = x_i \cap Y = y_j)*\)
- 边缘分布
\[ \begin{aligned}P_{i.} = \sum_jp(X = x_i \cap Y = y_j)\\P_{.j} = \sum_ip(X = x_i \cap Y = y_j)\end{aligned} \]
| \(x/y\) | \(y_1\) | \(y_2\) | \(...\) | \(y_n\) | |
|---|---|---|---|---|---|
| \(x_1\) | \(P_{ij}\) | \(P_i.\) | |||
| \(x_2\) | |||||
| \(...\) | |||||
| \(x_m\) | |||||
| \(P_{.j}\) |
- 条件分布
\[ P\left(Y=y_j / X=x_i\right)=\frac{p_{i j}}{p_i} \]
条件期望
条件期望是指在给定某个事件发生的条件下,另一个随机变量的期望值。
\[ E(Y|X = x_i) = \sum_jy_jP(Y = y_j|X = x_i) \]
全期望定理
如果随机变量Y的期望E(Y)存在,另一随机变量X的各种可能取值能将样本空间划分为不相交的事件,那么Y的期望就等于在X的每一个可能取值下,Y的条件期望和对应的概率的乘积之和。
\[ E(E(Y|X)) = E(Y) \]
条件方差
条件方差是在给定某个随机变量的条件下,另一个随机变量的方差。
\[ V(Y|X = x_i) = E[(Y-E(Y|X= x_i))^2|X = x_i] \]
全方差公式
如果Y是一个随机变量,X是另一个随机变量,那么Y的方差V(Y)可以被分解为:
\[ V(Y) = E(V(Y|X))+V(E(Y|X)) \]
- E[V(Y|X)]是在给定X的值的条件下Y的方差的期望
- V[E(Y|X)]是在给定X的条件下Y的期望的方差。
证明:
\[ \begin{aligned} V(Y) &= E((Y-E(Y))^2)\\ & = E((Y-E(Y|X)+E(Y|X)-E(Y))^2)\\ & = E((Y-E(Y|X))^2)+E[(E(Y|X)-E(Y))^2]\\ & + E[(Y-E(Y|X))(E(Y|X)-E(Y))]\\\end{aligned} \]
- 对第一项应用全期望公式
\[ \begin{aligned} E((Y-E(Y|X))^2)& = E[E((Y-E(Y|X))^2|X)]\\ & = E(V(Y|X))\end{aligned} \]
- 对第二项应用全期望公式
\[ \begin{aligned} E[(E(Y|X)-E(Y))^2]& = E[(E(Y|X)-E(E(Y|X)))^2]\\ & = V(E(X))\end{aligned} \]
- 交叉项
\[ \begin{aligned} E[(Y-E(Y|X))(E(Y|X)-E(Y))] = 0\end{aligned} \]
得到全方差公式
多元随机变量:连续
联合连续分布函数和密度函数
- \(\begin{aligned} & H(x, y) = P(X<x \cap Y<y)\\ & h(x, y) = \frac{\partial^2H}{\partial x \partial y}\end{aligned}\)
边缘分布
\(\begin{aligned} & f(x) = \int_{\mathbb{R}}h(x, y)dy\\ & g(y) = \int_{\mathbb{R}}h(x, y)dx\\ & \text{独立性条件:} \ h(x, y) = f(x)g(y)\end{aligned}\)
条件概率和贝叶斯公式
- 条件概率:\(g(y / x)=\frac{h(x, y)}{f(x)}\)
- 贝叶斯公式:
\[ g(y / x)=\frac{f(x / y) g(y)}{\int_R f(x / y) g(y) d y} \]
期望、方差、互相关
\[ E(Y / X=x)=\int_R y g(y / x) d y \]
\[ cov(X, Y) = E((X-EX)(Y-EY)) \]
\[ V(X+Y) = V(X)+V(Y)+2cov(X, Y) \]
相关系数,相关率
- 相关系数
相关系数是一个统计量,用于度量两个变量之间的相关(线性相关)程度。其值介于-1和1之间。
\[ \begin{aligned} \rho = \frac{cov(X, Y)}{\sigma_x \sigma_y}\end{aligned} \]
失效率
失效率,又称故障率,是描述产品、部件等在一定时间内失效的概率。它是一种衡量产品可靠性的重要指标。在概率论中,失效率函数(Hazard function)用来描述在某一时间点,给定到那一刻为止尚未发生的事件,在下一个微小的时间间隔内发生的条件概率密度。
法语翻译:Taux de défaillance
离散情况
\[ \lambda(t)=\frac{R\left(t_1\right)-R\left(t_2\right)}{\left(t_2-t_1\right) \cdot R\left(t_1\right)}=\frac{R(t)-R(t+\triangle t)}{\triangle t \cdot R(t)} \]
连续情况
\[ h(t)=\lim _{\Delta t \rightarrow 0} \frac{R(t)-R(t+\Delta t)}{\Delta t \cdot R(t)} \]
随机变量的收敛
- 随机变量的序列\(X_n\)被认为是依概率收敛于\(X\),如果对所有的正数\(\varepsilon\),当\(n\)趋向于无穷大时,\(P(|X_n - X| > \varepsilon)\)趋向于0。
- 对于一个随机变量序列\(X_n\),如果满足\(\lim_{n \to \infty} E[(X_n - X)^2] = 0\),则我们说序列\(X_n\)是平方平均收敛于\(X\)。
- \(L^p\)收敛是一种在\(L^p\)空间中的收敛方式,即对于一个随机变量序列\(X_n\),如果满足\(\lim_{n \to \infty} E[|X_n - X|^p] = 0\),其中\(p>0\),则我们说序列\(X_n\)是\(**L^p\)收敛**于\(X\)。
- 依分布收敛,也被称为弱收敛,是一种随机变量的收敛方式\(\mathbb{P}\left(X_n \leqslant a\right) \rightarrow \mathbb{P}(X \leqslant a)\)
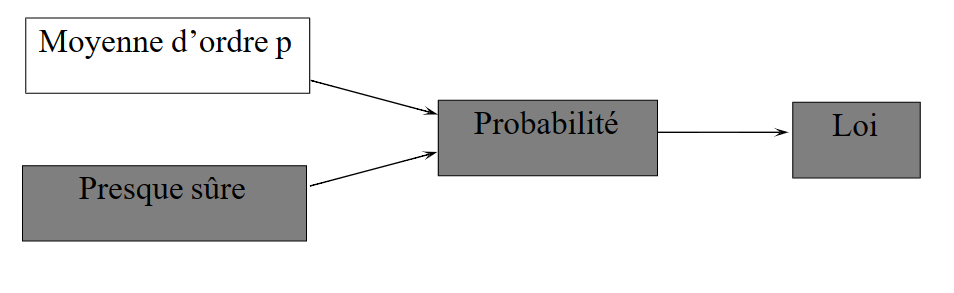
依概率收敛
依概率收敛(Convergence in Probability)是一种随机变量的收敛方式,用于描述一序列随机变量的行为。
收敛到常量
\[ \begin{aligned} &\forall \varepsilon \eta, \exists n_0, tel \ que\\ & n>n_0 \Rightarrow P(|X_n-a|>\varepsilon)<\eta\end{aligned} \]
- 根据切比雪夫不等式, \(*E(Xn) → a, V(Xn) → 0*\) 则收敛
收敛到另一个随机变量
\[ \begin{aligned} &\forall \varepsilon \eta, \exists n_0, tel que\\ &n>n_0 \Rightarrow P(|X_n-X|>\varepsilon)<\eta\end{aligned} \]
平方平均收敛和\(L^p\)收敛
\[ \lim_{n \to \infty} E[|X_n - X|^p] = 0 \]
几乎必然收敛
几乎必然收敛(Almost Surely Convergence),又称为以概率1收敛,是指一个随机变量序列\({X_n}\)几乎必然收敛于\(X\),如果满足\(P(\lim_{n \to \infty} X_n = X) = 1\)。在实际应用中,这意味着随着试验的进行,随机变量的值几乎必然会趋于某一固定值。这是一种比依概率收敛或平均平方收敛更强的收敛形式。
几乎必然相等
\[ P(\{\omega / X(\omega) \neq Y(\omega)\})=0 \]
几乎必然收敛
\[ P\left(\left\{\omega / \lim X_n(\omega) \neq X(\omega)\right\}\right)=0 \quad\left(X_n\right)_n \stackrel{\text { a.s. }}{\rightarrow} X \]
依分布收敛
依分布收敛(Convergence in Distribution),也称为弱收敛,是一种随机变量的收敛方式。当一个随机变量序列的分布函数逐点收敛于某一分布函数,我们就可以说这个随机变量序列依分布收敛于这个分布。
\[ \mathbb{P}\left(X_n \leqslant a\right) \rightarrow \mathbb{P}(X \leqslant a) \]
随机变量的性质和定理
莫瓦尔-拉普拉斯定理
莫瓦尔-拉普拉斯定理,也被称为二项式分布的中心极限定理,是概率论中的一个重要定理。该定理表明,当二项式分布的试验次数趋向无穷大时,二项式分布可以近似为正态分布。它是中心极限定理的一个特例。
二项分布可以由正态分布近似:
\[ B(n, p) \rightarrow LG(np, \sqrt{np(1-p)}) \]
条件
\[ np > 5, n(1 − p) > 5 \]
连续性修正-从连续到离散:
\[ \begin{aligned} &P_B(X = x) = P_{LG}(x-0.5<X<x+0.5)\\ &P_B(X <= x) = P_{LG}(x<x+0.5)\end{aligned} \]
连续性修正只有在:
使用连续分布近似分布;
必须有=时才使用连续性修正;
建议在最后只用连续性修正修正最终公式中出现的=。
大数定理
在一定条件下,随机变量序列的样本平均值以概率收敛于其期望值。
条件
\[ \begin{aligned} 1.&(x_n)_n \ \text{独立}\\ 2.¢rées, \ \text{或} \ E(x_i) = a\\ 3.&\text{方差存在, 且} \ \frac{1}{n^2}\sum_{i = 1}^{n}V(X_i)\rightarrow 0, n\rightarrow +\infty\end{aligned} \]
定理
\(\begin{aligned} \overline{X} = \frac{1}{n}\sum_{i = 1}^{n}x_i \xrightarrow[n \rightarrow \infty]{\text{依概率}}0(或a)\end{aligned}\)
中心极限定理
中心极限定理是概率论中最重要的一个基本定理。它表明,如果随机变量X1,X2,X3...Xn是独立同分布的,且具有相同的期望和方差,则随着样本量n的增大,这些随机变量的和的标准化值的分布将趋近于标准正态分布。
条件
\(\begin{aligned} 1.&(x_n)_n \ \text{独立} \ indépendant\\ 2.&\text{同分布} \ même \ loi\\ 3.&inconnue \ \text{可以不知道是什么分布}\\ 4.&\text{假设}\left\{ \begin{aligned} &E(x_i) = m\\ &V(x_i) = \sigma^2 \end{aligned} \right.\end{aligned}\)
则有
\[ \begin{aligned} &\frac{X_i+...+X_n-nm}{\sigma\sqrt{n}} \xrightarrow [n\rightarrow \infty]{en loi}LG(0, 1)\\ or \ & \sum_{i = 1}^{n}X_i\xrightarrow[n\rightarrow \infty]{}LG(nm, \sigma\sqrt{n})\\ or \ & \frac{\frac{1}{n}\sum^n_iX_i-m}{\sigma/\sqrt{n}}\xrightarrow[n\rightarrow \infty]{}LG(0, 1)\\ or \ & \overline{X}\xrightarrow[n\rightarrow \infty]{}LG(m, \sigma/\sqrt{n})\end{aligned} \]
最后一个最为重要