Basics
Basics
Chapitre 3
重要单词
| Saturated Mixture | 饱和混合物 |
|---|---|
| Saturated liquid | 饱和液体 |
| super-heated vapor | 过热蒸汽 |
| compressed liquid | 过冷液体 |
| initial specific volume | 初始单位质量体积 |
| final state | 最终状态 |
| quality | 质量分数 |
| compressible factor | 压缩系数 |
| reduced pressure&reduced temperature | 临界压力和临界温度 |
| Enthalpy | 焓 |
| entropy | 熵 |
| internal energy | 内能 |
主要内容
Quality 质量分数
质量分数是气态物质占总体的比例
\(y = y_f+xy_{fg}\)
The compressiblility chart
首先计算折算压力和折算温度
\(T_{R}={\frac{T}{T_{C r}} \quad P_{R}=\frac{P}{P_{C r}}}\)
- 其中\(P_{cr}\)和\(T_{cr}\)分别代表临界压力和临界温度reduced pressure&reduced temperature。
在compressiblility chart 中查找compressible factor 压缩系数。
以此计算最终的体积
\[ V = Z\cdot V_{ideal} \]
查表
- 对于saturated mixture,saturated liquid,saturated
vapor,他们的所有enthalpy, entropy, specific volume和internal
energy需落在表中相应温度或压强给出的区间。
- 对于这些状态可以直接查出T,P
- 如果是saturated mixture,则需要使用上述质量分数的式子计算enthalpy, entropy, specific volume和internal energy
- 对于compressed liquid和superheated vapor
- 可以直接查出P
- T和内能等其他数据需要知道一个查另一个,需要线性插值
Chapitre 4
主要单词
| quais-equilibrium | 准稳态 |
|---|---|
| ideal gaz | 理想气体 |
| kinetic and potential energy | 动能和势能 |
| with variable specific heats | 有可变潜热 |
| negligible | 可忽略的 |
| back work ratio(BWR) | 压缩功与膨胀功之比 |
| isobaric process | 等压过程 |
| polytropic process | 多方过程 |
| isothermal process | 等温过程 |
主要内容
体积功的计算
- 通式:\(W_{b}=\int_{1}^{2} P \cdot d U\)
- isobaric process 等压过程:\(W_{b}=P_{0} \cdot\left(V_{2}-V_{1}\right)\)
- polytropic process 多方过程:
- \(P V^n=c\)
- \(W_b=\int_1^2 P \cdot d V=\int_1^2 V^{-n} \cdot c d V=\frac{P_2 V_2-P_1 V_1}{1-n}\)
- isothermal process of an ideal gaz 理想气体的等温过程
- \(W_{b}=m R T_{0} \ln \frac{V_{2}}{V_{1}}\)
- \(W_{b}=m R T_{0} \ln \frac{P_{1}}{P_{2}}\)
内能,焓与潜热
- internal energy 内能
- \(Q_{\text {in }}-W_{\text {out }}=\Delta U\)
- \(\Delta u=\int_1^0 C_v(T) d T \cong C_{v \cdot a v g}\left(T_2-T_1\right)\)
- enthalpy 焓
- \(W_{b}+\Delta U=\Delta H\)
- \(W_{in}+Q_{in} = \Delta H\)
- \(\Delta h=\int_1^2 C_p(T) d T \cong C_{p \cdot a v g}\left(T_2-T_1\right)\)
- \(C_p=C_v+R\)
Chapter 5
主要单词
| steady flow | 定常流动 |
|---|---|
| mass flow rate | 质量流速度 |
| volume flow rate | 体积流速度 |
主要内容
单向定常流动的平衡方程
$$
{ \[\begin{array}{l} m_{1}=m_{2} \rightarrow \frac{1}{\nu_{1}} V_{1} A_{1}=\frac{1}{\nu_{2}} \cdot V_{2} A_{2} \\ \left.\dot{Q}-\dot{W}=\dot{m}\left[h_{2}-h_{1}+\frac{V_{2}^{2}-V_{1}^{2}}{2}+g ( z_{2}-z_{1}\right)\right] \end{array}\].
$$
- 使用这两个方程都需要steady-flow的assumption
- 使用第一个方程往往会涉及specific volume is constant
- 使用第二个方程往往会涉及:
- heat loss is negligible
- changes in kinetic and potential energies are negligible
- specific heat is constant
一种特殊的题型
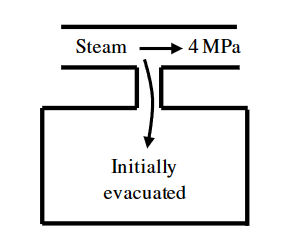
气体在supply line中恒压流动,打开阀门为一个真空的tank充气。在这个过程中有:
- \(h_{\text {line }}=u_{\text {tank
}}\)
- 基于这个等式可以建立两边的关系
- \(w_{\text {flow }}=h_{\text {line
}}-u_{\text {line }}\)
- 用于计算flow work
Chapter 6
主要单词
| operate steadily | 稳定的运行 |
|---|---|
| PMM | 永动机 |
| completely reversible | 完全可逆 |
主要内容
本章主要涉及热机效率的定义和运算,以及与卡诺热机和逆卡诺热机的效率比较
热机效率和性能系数
$$
\[\begin{aligned}&\eta_{\text {rev. th }}=1-\frac{T_{L}}{T_{H}}\\ & COP_{R,{\text {rev }}}=\frac{1}{T_{H} / T_{L}-1} \\ & COP_{HP,rev} =\frac{1}{1-T_{L} / T_{H}} \end{aligned}\]$$
卡诺热机效率和性能系数
$$
\[\begin{aligned}&\eta_{\text {rev. th }}=1-\frac{T_{L}}{T_{H}}\\ & COP_{R,{\text {rev }}}=\frac{1}{T_{H} / T_{L}-1} \\ & COP_{HP,rev} =\frac{1}{1-T_{L} / T_{H}} \end{aligned}\]$$
Chapter 7
主要单词
| isentropic | 等熵的 |
|---|---|
| entropy | 熵 |
| abiabatic | 绝热的 |
| specific heat ratio | 热熔比 |
| incompressible | 不可压缩的 |
| reversible | 可逆的 |
主要内容
本章的主要内容涉及熵的计算和等熵设备的计算
理想气体熵的计算
\[ \begin{aligned} & S_2-S_1=C_{V \text { avg }} \ln \frac{T_2}{T_1}+R \ln \frac{V_2}{V_1} \\ & S_2-S_1=C_{P \text { avg }} \ln \frac{T_2}{T_1}-R \ln \frac{P_2}{P_1} \end{aligned} \]
等熵过程等式
\[ \begin{aligned} & \left(\frac{T_2}{T_1}\right)_{s=\text { const }}=\left(\frac{P_2}{P_1}\right)^{\frac{k-1}{k}} \\ & \left(\frac{T_2}{T_1}\right)_{s=\text { const }}=\left(\frac{v_1}{v_2}\right)^{k-1} \\ & \left(\frac{P_2}{P_1}\right)_{s=\text { const }}=\left(\frac{V_2}{V_1}\right)^k \end{aligned} \]
等熵设备的稳态流功
\[ W_{\text {rev }}=-\int_{1}^{v} v \cdot d_{p}-\Delta K_{e}-\Delta{p_ e} = -V(P_1-P_2) \]
等熵条件的应用方式
- 如果可以查表,则从信息完整的一方查出熵值,利用等熵的条件去查不完整的一方的熵值
- 如果不可以查表,则需利用等熵过程等式建立两方的关系
Chapter 12
主要单词
| Clapeyron equation | 克拉佩龙方程 |
|---|---|
| difference specific heat | 潜热差 |
| throttling process | 节流过程 |
| Joule-Thomson coefficient | 焦耳-汤姆逊参数 |
| generalized enthalpy or entropy departure charts | 广义熵或熵出发图 |
| generalized chart | 广义图 |
主要内容
这部分内容相对比较陌生,建议在复习结束之后再次回顾这部分习题
克拉佩龙方程
\[ \ln \left(\frac{P_2}{P_1}\right)_{\text {sat }} \cong \frac{h_{f g}}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)_{\text {sat }} \]
几组微分方程
\[ \begin{aligned}& d u=c_v d T+\left[T\left(\frac{\partial P}{\partial T}\right)_v-P\right] d V \\& d h=c_p d T+\left[U-T\left(\frac{\partial V}{\partial T}\right)_P\right] d P \\& d s=\frac{c_v}{T} d T+\left(\frac{\partial P}{\partial T}\right)_v d V\\&d s=\frac{c_p}{T} d T-\left(\frac{\partial V}{\partial T}\right)_P d P\end{aligned} \]
潜热差
\[ \begin{gathered}c_p-c_v=-T\left(\frac{\partial V}{\partial T}\right)_P^2\left(\frac{\partial P}{\partial V}\right)_T \\c_p-c_v=\frac{V T \beta^2}{\alpha}\end{gathered} \]
焦耳-汤姆逊系数
\[ \mu_{\mathrm{JT}}=\left(\frac{\partial T}{\partial P}\right)_h=-\frac{1}{c_p}\left[V-T\left(\frac{\partial V}{\partial T}\right)_p\right] \]
广义熵、焓、内能
\[ \begin{aligned}\bar{h}_2-\bar{h}_1 & =\left(\bar{h}_2-\bar{h}_1\right)_{\text {ideal }}-R_u T_{\mathrm{cr}}\left(Z_{h_2}-Z_{h_1}\right) \\\bar{u}_2-\bar{u}_1 & =\left(\bar{h}_2-\bar{h}_1\right)-R_u\left(Z_2 T_2-Z_1 T_1\right) \\\bar{s}_2-\bar{s}_1 & =\left(\bar{s}_2-\bar{s}_1\right)_{\text {ideal }}-R_u\left(Z_{s_2}-Z_{s_1}\right)\end{aligned} \]
其中\(Z_h\),\(Z_s\)需要通过\(\begin{gathered}T_{R 1}=\frac{T_1}{T_{\mathrm{cr}}} \quad P_{R 1}=\frac{P_1}{P_{\mathrm{cr}}}\end{gathered}\)来查表获得
节流过程
利用节流过程焓不变的条件建立两个状态的关系



